非分配格上二型模糊集真值代数子代数的构造
宋翔宇,王学平
(四川师范大学 数学科学学院,四川成都 610066)
§1 引言
1975年,Zadeh将模糊集扩展为二型模糊集(见[1]).之后,二型模糊集特别是二型模糊集真值代数的研究受到国内外学者的极大关注,如:研究二型模糊集的代数运算(见[2]),讨论二型模糊集真值代数的代数结构(见[3-6]),研究二型模糊集真值代数上的蕴含(见[7]),凸正规函数的格结构与拓扑结构(见[8])及三角模(见[9]).二型模糊集的真值代数是由从单位区间到单位区间的所有函数组成的集合及函数的卷积运算一起组成的代数结构(见[10-11]).最近,De Miguel等将二型模糊集从单位区间扩展为有界格,定义了函数的卷积运算,研究了有界格上二型模糊集真值代数的代数结构,构造了有界分配格上二型模糊集真值代数的有界分配子代数及Birkhoff系统(见[12]).文献[12]中许多结论都需要格是分配的,为此他们提出了如下公开问题.
当有界格不是分配格时,更加深入地研究卷积运算,包含以下两个方面.
(i) 寻找Na ∩I ∩C的子集G,使得G在卷积运算之下也是封闭的,并且构成有界格(Na,I与C的定义见第二节);
(ii) Birkhoff方程的研究.
2019年,严卫平与王学平也研究了有界格上二型模糊集真值代数的代数结构及其性质(见[13]).特别地,刘志强与王学平在文[14]中构造了有界非分配格上Na ∩I ∩C的一个Birkhoff系统及一个有界分配子格,从一个侧面回答了上面开问题.本文继续研究上面开问题,将构造有界非分配格上Na ∩I ∩C的一个有界分配子格及一个Birkhoff系统.
§2 预备知识
为方便,先回顾文献[15]中一些基本概念.设(L,≤)为偏序集,如果对任意x,y ∈L,inf{x,y}在L中存在(记为x ∧y),则称(L,≤)为交半格.如果对任意x,y ∈L,sup{x,y}在L中存在(记为x ∨y),则称(L,≤)为并半格.如果对任意x,y ∈L,inf{x,y}与sup{x,y}在L中均存在,则称(L,≤)为格.也记格(L,≤)为(L,∧,∨).由此可见,格既是交半格又是并半格.如果格(L,≤)有最小元0和最大元1,则称(L,≤)为有界格.如果格(L,∧,∨)满足:对任意a,b,c ∈L,a ∧(b ∨c)=(a ∧b)∨(a ∧c)与a ∨(b ∧c)=(a ∨b)∧(a ∨c)成立,则称(L,∧,∨)为分配格.因为a ∧(b ∨c)=(a ∧b)∨(a ∧c)与a ∨(b ∧c)=(a ∨b)∧(a ∨c)等价,因此,要证明格的分配性仅需验证一条即可.如果格(L,≤)的任意子集B的infB与supB在L中均存在,则称(L,≤)为完备格.如果完备格(L,∧,∨,0,1)满足:对任意a ∈L,∅≠B ⊆L,有成立,则称(L,∧,∨,0,1)为frame.如果有两个运算的代数结构(L,∧,∨)满足:(1) (L,∧)是交半格,(L,∨)是并半格;(2) 对任意a,b ∈L,a ∨(a ∧b)=a ∧(a ∨b);则称(L,∧,∨)为Birkhoff系统.
本节设L1=(L1,∨1,∧1,01,11)为有界格,L2=(L2,∨2,∧2,02,12)为frame,对应的序关系分别为≤1and≤2.设F={f|f:L1→L2}.
定义2.1(见[12]) 对任意f,g ∈F,

以下统一使用符号∨,∧,≤和≥分别表示格中上确界,下确界,小于等于及大于等于.为了方便起见,给出一些必要的符号描述如下(见[12]).
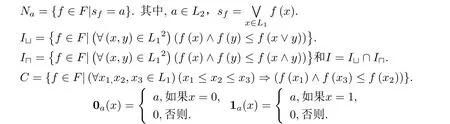
定义2.2(见[15]) 设(L,≤) 为格,a ∈L.如果a=x ∨y蕴涵a=x或a=y,则称a是并既约元.对偶地,如果a=x ∧y蕴涵a=x或a=y,则称a是交既约元.
定义2.3(见[15]) 设(E,≤)为偏序集,a,b ∈E并且a 引理2.1(见[12]) 任意a ∈L2,代数结构(Na ∩I ∩C,,,0a,1a)是有界格当且仅当L1是分配格. 引理2.2(见[15]) 格L是非分配格当且仅当它包含有形如N5或M3的子格. 图1 N5 图2 M3 以下,进一步假设N5⊆L1或M3⊆L1且L1是满足如下二个条件的有界格. (a) 如果N5⊆L1,则x1在L1中有唯一下邻及x2与x4两个上邻,x5在L1中有唯一上邻及x3与x4两个下邻,且任意x ∈{x2,x3,x4}在L1{x1,x2,x3,x4,x5}中既无下邻也无上邻. (b) 如果M3⊆L1,则y1在L1中有唯一下邻及y2,y3与y4三个上邻,y5在L1中有唯一上邻及y2,y3与y4三个下邻,且任意y ∈{y2,y3,y4}在L1{y1,y2,y3,y4,y5}中既无下邻也无上邻. 设 下面讨论S ∩Na ∩I ∩C的代数性质.由文献[12]的命题6知下面命题成立. 命题3.1设a ∈L2,f,g ∈Na,则(i);(ii). 命题3.2设f,g ∈S ∩I ∩C,则(i);(ii). 证以下仅证明(i),(ii)类似可证.因为,所以由文献[12]的命题7有.为最终证明,以下仅需证明.因为f,g ∈I=,所以对任意x1,x2∈L1, 因为u1≤x1和u2≤x2,所以u1∧u2≤x1∧x2.因此u1∧u2≤(x1∧x2)∧(u1∨u2)≤u1∨u2.类似地,v1∧v2≤(x1∧x2)∧(v1∨v2)≤v1∨v2成立.因为f,g ∈C,所以有 显然[(x1∧x2)∧(u1∨u2)]∨[(x1∧x2)∧(v1∨v2)]≤(x1∧x2)∧[(u1∨u2)∨(v1∨v2)].分以下两种情况讨论. (1)如果[(x1∧x2)∧(u1∨u2)]∨[(x1∧x2)∧(v1∨v2)]=(x1∧x2)∧[(u1∨u2)∨(v1∨v2)],则[(x1∧x2)∧(u1∨u2)]∨[(x1∧x2)∧(v1∨v2)]=(x1∧x2)∧[(u1∨v1)∨(u2∨v2)]=x1∧x2.令u=(x1∧x2)∧(u1∨u2)和v=(x1∧x2)∧(v1∨v2),于是 (2)如果[(x1∧x2)∧(u1∨u2)]∨[(x1∧x2)∧(v1∨v2)]<(x1∧x2)∧[(u1∨u2)∨(v1∨v2)],则分以下两种情况. (a) 如果u1∨u2,x1∧x2,v1∨v2中有两元可比,则断言u1∨u2 (b)如果u1∨u2,x1∧x2,v1∨v2中元两两不可比,则n=(v1∨v2)∧(u1∨u2),v1∨v2,u1∨u2,x1∧x2,m=(v1∨v2)∨(x1∧x2)构成与M3同构的五元子格.于是 因此,由(a)和(b)知()(x1)∧()(x2)≤()(x1∧x2). 综合(1)与(2)知,对任意x1,x2∈L1,()(x1)∧()(x2)≤()(x1∧x2),即. 命题3.3设f,g ∈S ∩I ∩C,则(i);(ii). 证以下仅证明(i),(ii)类似可证.设x1,x2,x3∈L1使得x1≤x2≤x3.因为f,g ∈I,有 又u1∧u3≤x1≤x2,有u1∧u3≤x2∧(u1∨u3)≤u1∨u3.类似地,有v1∧v3≤x2∧(v1∨v3)≤v1∨v3.因为f,g ∈C,所以 显然[x2∧(u1∨u3)]∨[x2∧(v1∨v3)]≤x2∧[(u1∨u3)∨(v1∨v3)].分两种情况. (1)如果[x2∧(u1∨u3)]∨[x2∧(v1∨v3)]=x2∧[(u1∨u3)∨(v1∨v3)],则[x2∧(u1∨u3)]∨[x2∧(v1∨v3)]=x2∧[(u1∨v1)∨(u3∨v3)]=x2∧(x1∨x3)=x2.令u2=x2∧(u1∨u3)和v2=x2∧(v1∨v3),于是 (2)如果[x2∧(u1∨u3)]∨[x2∧(v1∨v3)] (a) 如果v1∨v3,u1∨u3,x2有两元可比,则断言u1∨u3 (b) 如果v1∨v3,u1∨u3,x2两两不可比,则n=(u1∨u3)∧(v1∨v3),v1∨v3,u1∨u3,x2及m=x2∨(v1∨v3)构成与M3同构的五元子格.于是 由(a)与(b)知()(x1)∧()(x3)≤()(x2). 综合(1)与(2)知,对任意x1,x2,x3∈L1,如果x1≤x2≤x3,则()(x1)∧()(x3)≤()(x2),即. 命题3.4设f,g ∈S,则(i);(ii). 证以下仅证明(i),(ii)类似可证.对任意f,g ∈S,分如下三种情况. (1)L1只含有子格N5. 因为x1和x2都是L1中的并既约元,所以 由格L1满足的条件知,对任意x ∈L1,x 类似可以证明()(x3)=()(x4)=()(x1).另外 图3 定理3.5设a ∈L2,则代数结构(S ∩Na ∩I ∩C,,0a,1a)是有界分配格. 证设f,g,h ∈S ∩Na ∩I ∩C,则对任意x ∈L1,因为L1是非分配格,所以 当u ∨(v ∧w)≠(u ∨v)∧(u ∨w)时,分以下两种情况. (a) 如果u,v,w有两元可比,则断言u (b) 如果u,v,w两两不可比,则n=u ∧w,u,v,w及m=v ∨w构成与M3同构的五元子格.类似于(a)可以证明 综合(a)与(b)知 以下证明()(f h)(). 对任意x ∈L1,因为f ∈I=,所以 因为u1∧u2≤x,所以u1∧u2≤x ∧(u1∨u2)≤u1∨u2.又因为f ∈C,所以 因为v ∧w ≤x,x ∧(u1∨u2)≤x,所以 显然(x ∧(u1∨u2))∨(v ∧w)≤(x ∨(v ∧w))∧((u1∨u2)∨(v ∧w)).以下分两种情况讨论. (I) 如果(x ∧(u1∨u2))∨(v ∧w)<(x ∨(v ∧w))∧((u1∨u2)∨(v ∧w)),则断言v ∧w (i) 当w=v或w=x或w=p时,x ∧(u1∨u2)=q.又由f,g,h ∈S,故f(x ∧(u1∨u2))=f(q)=f(x),g(v)=g(v ∧w)=g(x),h(w)=h(x).于是 (ii)当w >p时,w >p>u1∨u2≥u2.而u1∨v ≤(u1∨u2)∨v=(u1∨u2)∨(v ∧w)=p 综合(i)与(ii)知 (II)如果(x ∧(u1∨u2))∨(v ∧w)=(x ∨(v ∧w))∧((u1∨u2)∨(v ∧w)),则显然(u1∨u2)∨(v ∧w)≤((u1∨u2)∨v)∧((u1∨u2)∨w).分下面两种情况. (1)如果(u1∨u2)∨(v ∧w)=((u1∨u2)∨v)∧((u1∨u2)∨w),则(x ∧(u1∨u2))∨(v ∧w)=(x ∨(v ∧w))∧((u1∨v)∨u2)∧((u2∨w)∨u1)≥x.所以由公式(2)知(x ∧(u1∨u2))∨(v ∧w)=x.令u=x ∧(u1∨u2),所以 (2) 如果(u1∨u2)∨(v ∧w)<((u1∨u2)∨v)∧((u1∨u2)∨w),则分下面两种情况. (a) 如果u1∨u2,v,w有两元可比,则断言u1∨u2 (a1) 当u2=u1时,x=(u1∨v)∧(u2∨w)=v ∧p=v,x ∧(u1∨u2)=v ∧u1=u1,又因为f,g,h ∈S,所以f(x ∧(u1∨u2))=f(u1)=f(u1∨u2)=f(v)=f(x),g(v)=g(x),h(w)=h(v)=h(x),于是 (a2)当u2 综合(a1)与(a2)知(()())(x)≤f(x)∧g(x)∧h(x). (b) 如果u1∨u2,v,w两两不可比,则n=(u1∨u2)∧v,u1∨u2,v,w及m=v ∨w构成与M3同构的五元子格.用类似的方法可以证明(()())(x)≤f(x)∧g(x)∧h(x). 综合(a)与(b)知 定理3.6代数结构(,)是Birkhoff系统. 对任意x ∈L1,因为L1是非分配格,所以 当u1∨(u2∧v)≠(u1∨u2)∧(u1∨v)时,分以下两种情况: (a)如果u1,u2,v有两元可比,则断言u1 (b) 如果u1,u2,v两两不可比,则n=u1∧v,u1,u2,v及m=u1∨v构成与M3同构的五元子格.类似(a)可以证明 综合(a)与(b)知,当存在u1,u2,v ∈L1使u1∨(u2∧v)≠(u1∨u2)∧(u1∨v)时 本文构造了有界非分配格L1与frameL2之间函数的一个子集,证明了该子集与函数的卷积运算构成一个有界分配格,最后构造了一个Birkhoff系统.通过比较不难发现,本文中的非分配格L1与文献[14]中所选非分配格L1不同,且文献[14]中构造的真值代数的子代数Fa也与本文构造的真值代数的子代数S不同.不难发现,本文及文献[14]讨论的是在非分配格L1固定的情况下,选择有界非分配格L1与frameL2之间满足一定条件的函数,从而使函数所构成的集与函数的卷积运算构成一个有界分配格以及一个Birkhoff系统.因此,一个值得研究的问题是:在非分配格L1固定的情况下,要使有界非分配格L1与frameL2之间的函数所构成的集与函数的卷积运算构成一个有界分配格以及一个Birkhoff系统,问这些函数一定要满足什么条件?

§3 真值代数子代数的构造



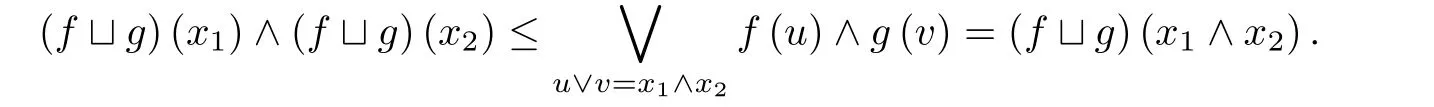





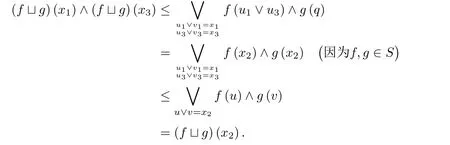

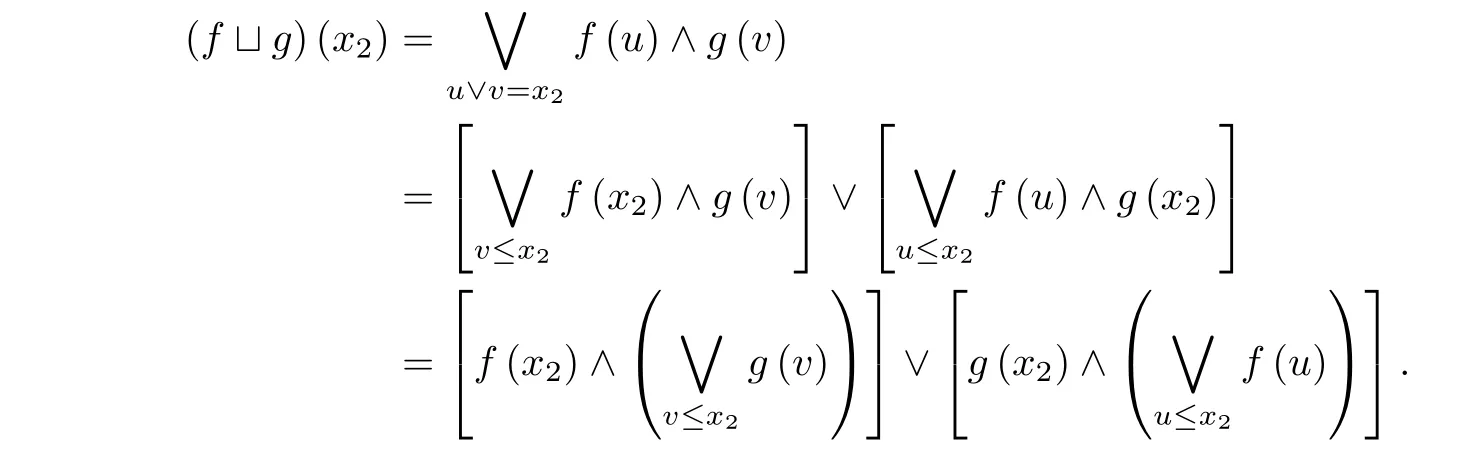



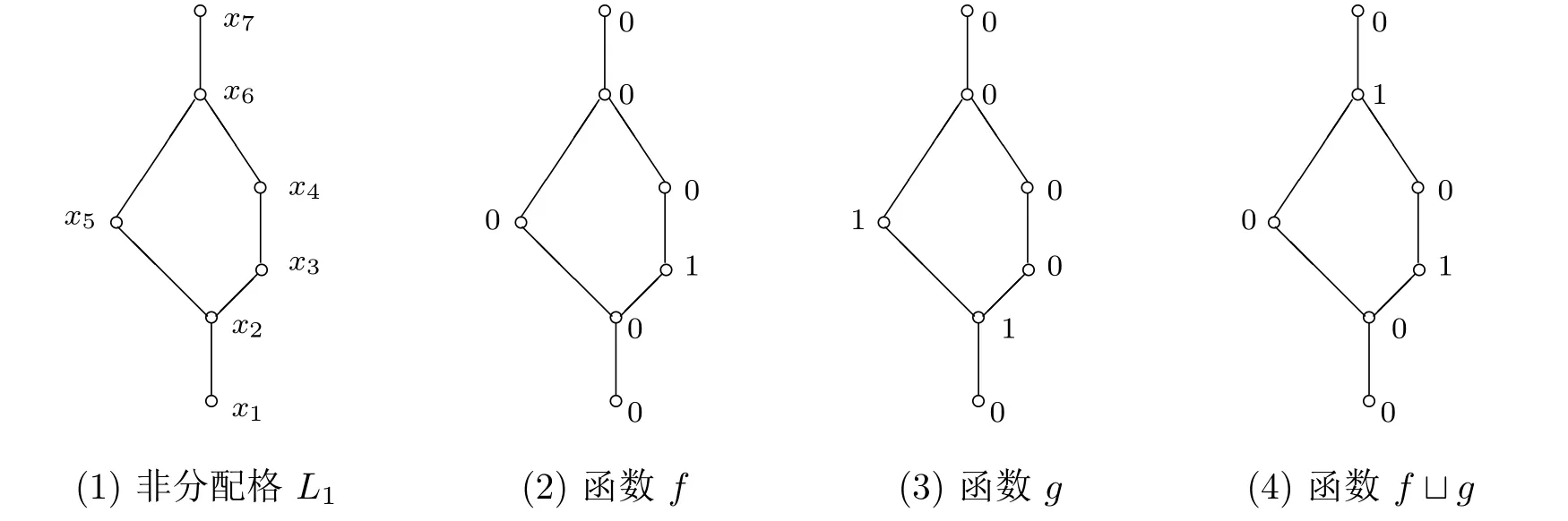
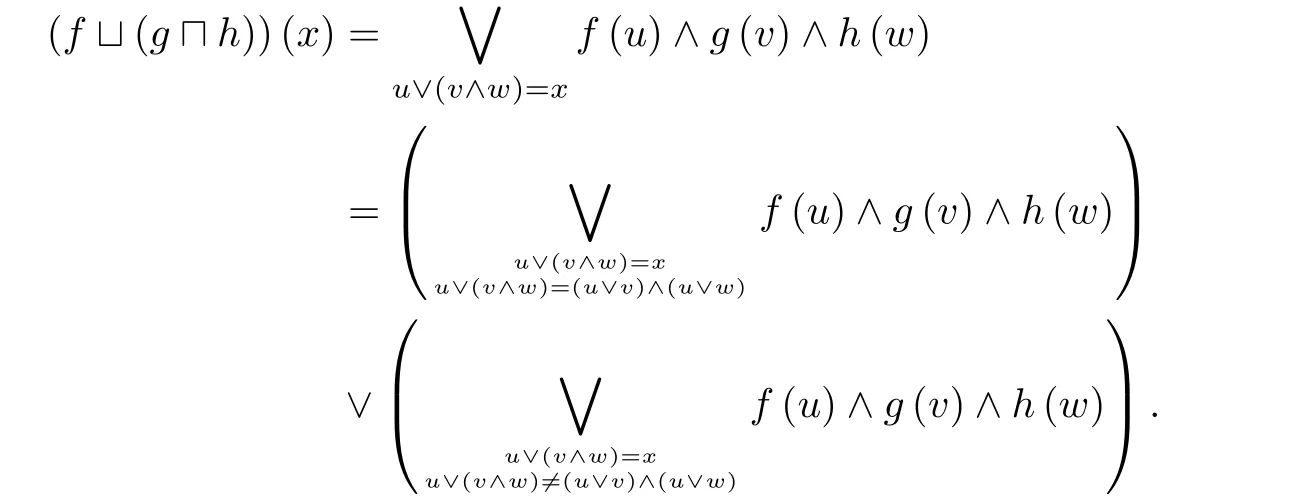
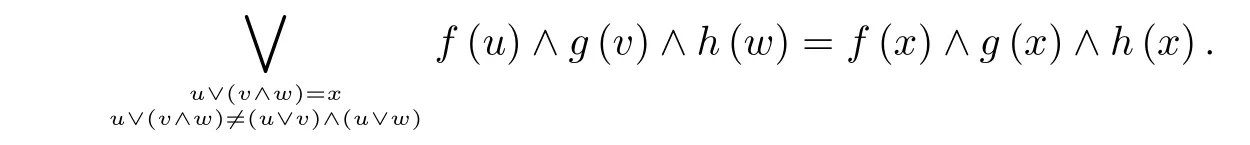




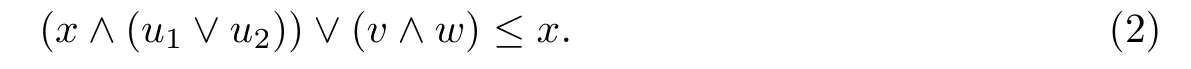





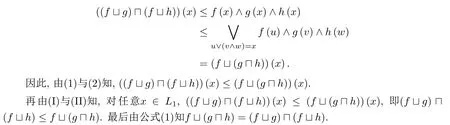

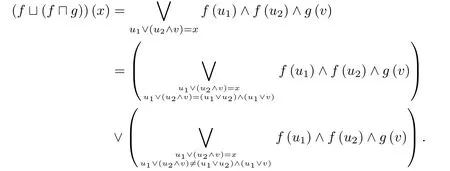



§4 结束语

