混行环境下CACC 系统驾乘舒适性优化控制

梁 军 ，于 扬 ，王文飒 ，陈 龙

（江苏大学汽车工程研究院，江苏 镇江 212013）

随着车路协同技术的不断发展，传统道路交通系统中车辆原本无法显现的自组织、网络化、非线性、强耦合等特性逐渐凸显出来. 交通系统属性的变化使得传统研究方法难以适用. 同时，自动驾驶技术的不断进步一并催生出网联自动车辆（connected automated vehicle，CAV）与人工驾驶车辆（manual vehicle，MV）长期共存的交通新态势[1]，这种交通组织成分的变化对模型复杂度提出更高要求. 车辆不再有主次之分，所有车辆全部为分散目标，交通系统需被作为开放的复杂系统进行研究. 在CAV 与MV组成的混行交通流新常态下，协同自适应巡航控制（cooperative adaptive cruise control，CACC）作为CAV 的关键功能辅助，安全性和稳定性研究取得系列成果，但驾乘舒适性研究明显不足. 因此，有必要对混行这一新环境下CACC 系统的驾乘舒适性进行新的探索.

CACC 急加速或急减速会引起生理上的不舒适，跟车间距过近或跟车间距误差过大会造成心理上的不舒适. 对于舒适度的判断准则大体一致，包括：急动度（加速度变化率）越小越好[2]；加速度越小越好[3]；对于给定加速度，急动度越小越舒适[4]；由车体横向震动引起的约为0.2 Hz 低频加速度易诱发晕车[5-7]. 当前，对CAV 驾乘舒适性影响的研究还不全面. Elbanhawi 等[8]总结了CAV 路径规划的舒适性，强调了CAV 队列行驶舒适性的重要性；Milakis 等[9]将驾乘舒适性划分为CAV 的一级影响. 从宏观角度来看，驾乘舒适性受加速度、速度波动影响，与交通流稳定性密切相关[10]，因速度、加速度波动而偏离稳态后，会产生不舒适感. 因此，CAV 交通流稳定性优化成为提升驾乘舒适性的重要手段，但这方面研究仍存在较大空白[8-11]. 在纯CAV 环境下，对跟车模型进行稳定性分析是提升舒适性的常见思路[12-15]. Zhou等[16]提出具有局部稳定性、多准则队列稳定性的串行分布式模型预测控制（model predictive control，MPC）方法，但不完全适用于混行环境. 鉴于车辆动力学、执行机构的差异，仅从交通流稳定性考虑难以保证单车舒适性最优，还需从微观角度进行进一步优化[17-18].

因此，本文以CACC 系统的运行舒适性为研究目标，设计考虑驾乘舒适性的双层控制策略（duallayer control strategy considering ride comfort，RCDCS）. 上层控制器从宏观角度出发，根据MV 行车状态，以舒适性为优化目标，及时调整车队整体的跟车间距和速度；下层控制器则从微观角度出发，根据车队中不同车辆的动力学情况，利用油门、制动踏板切换策略优化车辆动力输出，保证每辆车达到最优行车状态.

1 CACC 系统运行舒适度优化模型

1.1 CACC 系统舒适度优化框架模型

CACC 系统包括车辆控制系统、通信系统和人机交互界面，其系统架构如图1 所示. 人机交互界面一方面为驾驶员提供跟车基本信息和自车控制信息，另一方面可以控制和调整CACC 系统的运行状态. 车辆控制系统采用由上层控制器和下层控制器组成的双层控制结构，上层控制器负责队列的跟随控制，协同车辆间的跟车间距、跟车速度，下层控制器负责车辆的加速度控制. 由于系统配备了跟踪算法[19]，因此根据驾驶员设定的跟车时距，融合传感器获取的数据，通过无线通信接收前车终端传输的速度、加速度信息计算出期望速度和加速度，然后将控制结果反馈至上层目标控制函数，根据当前状态生成相应加速或者制动命令并传输至车辆平台，从而使车辆按预设的状态行驶.

图1 CACC 系统舒适度优化分层架构Fig. 1 Hierarchical architecture of CACC system

CACC 系统的工作模式如图2 所示. 当CACC系统启用时，系统会根据控制策略设定队列车辆的运行方式，同时上层控制系统会判断与自车直接通信的车辆身份标识号（identity document，ID）和与测距传感器检测到的车辆ID 是否相同. 若检测到目标变更，控制器会重新获取新目标信息，根据跟车策略重新计算跟车间距和期望加速度，并交由下层控制器执行，同时对上层结果进行反馈. 当传输信号故障时，系统的工作状态会变为失活，提醒驾驶员进行人工操作.

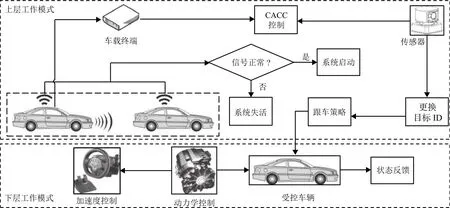
图2 CACC 系统工作模式Fig. 2 Working mode of CACC system

1.2 RC-DCS 控制策略

1.2.1 上层控制策略设计

首先建立CACC 控制系统的纵向动力学模型，如式（1）～（5）所示.

式（1）～（5）中：Te为发动机扭矩；E(•)为发动机静态特性的非线性函数；ne为发动机转速；α为油门开度；Te,act为发动机实际扭矩；τe为发动机时间常数；J为飞轮惯性；Tp为液力变矩器的泵扭矩；CT(•)为变矩器的容量系数；λ为变矩器的转速比；Tt为变矩器的涡轮扭矩[20]；RT(•)为变矩器的扭矩比；ig为变速箱传动比；i0为终传动比；r为车轮半径；v为后车车速；η为传动系统效率；M为车辆质量；g为重力加速度；Ca为空气阻力系数；S为前横截面积；ρ为空气密度；f为滚动阻力系数；θ为道路坡度；δ为集中系数；I为四车轮惯性矩.

上层控制器采用由与领航车相对速度和跟车间距误差表征的车辆纵向动力学和车辆间纵向动力学的两状态空间模型，可由式（6）、（7）计算求得.

式（6）～（8）中：vrel为领航车与后车相对速度；vp为领航车速度；de为跟车间距误差；d为实际跟车间距；ddes为期望跟车间距；doff为补偿距离[21-22]，根据经验取值为1.5 m；h为可变车头时距；h0为标称车头时距，取值2.5；cv、kv为大于0 的常数.

显然，控制策略是线性反馈，可以实现将车辆动力学线性化，并通过车辆动力学排除一些特征参数简化系统模型.

行驶过程中，考虑第i辆车与前车的通信时延，得到式（14）所示的CACC 系统状态空间方程.

对于跟随车辆，在保证尽可能小的速度误差和距离误差的前提下，定义了代价函数L来优化行驶的稳定性和舒适性，如式（16）所示.

当自车行驶速度小于巡航速度时，W1= (0.01,1.00, 0.10)T，W2= 8，K= (0.03, 0.39, −0.22)T；行驶速度等于巡航速度时，W1= (0.40, 1.00, 0.10)T，W2= 1，K=(0.63, 0.96, −0.43)T；行驶速度大于巡航速度时，W1=(0.60, 1.00, 0.15)T，W2= 2，K= (0.93, 1.20, −0.68)T.

1.2.2 下层控制策略设计

在混行环境中，当CACC 车辆跟随MV 时，仅依靠上层跟车模型无法很好满足乘坐舒适性，分析发现车辆起步时存在振幅过大、波动频率过高的问题，为此设计基于模糊理论的下层控制器优化加速度输出，利用模糊理论优化油门、制动踏板切换逻辑，保证CACC 车辆退化为ACC 车辆后的舒适性.

根据驾驶规则，制动踏板基本操作逻辑与油门踏板相反，因此其模糊控制器与油门踏板相同. 唯一区别是制动控制器输出制动力矩变化量与油门控制器的输出相反，如式（20）所示，则当前制动力矩百分比如式（21）所示.

式中：b(n)、Δb(n)分别为在第n个离散时间步长的制动百分比、制动百分比变化量.

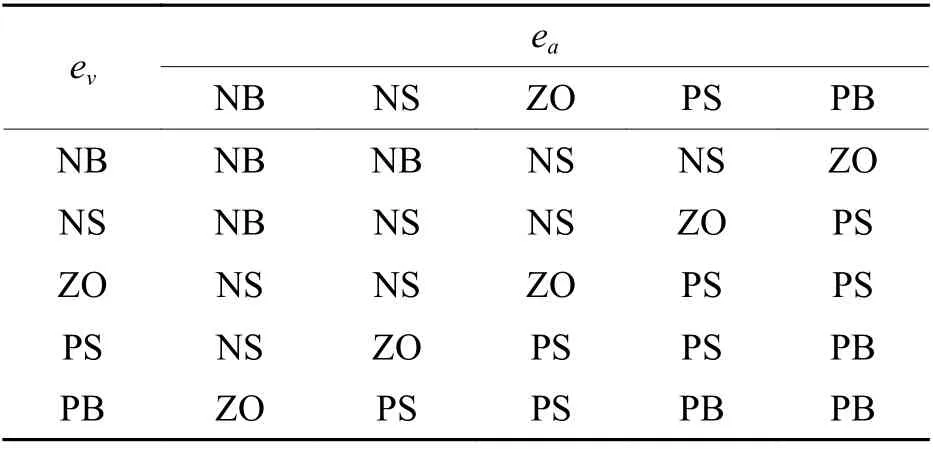
表1 控制规则表Tab. 1 Control rules

由于油门开度和制动力矩是两个物理意义、标度不同的变量[23]，通过百分比表示可以将两个输出值统一到 [0,1]，从而将制动控制器与油门控制器简化为一个控制器.

为保证油门和制动控制器协调工作，设计切换控制器如下：1） 避免两踏板同时工作；2） 踩下油门踏板前需抬起制动踏板，反之亦然；3） 避免频繁切换油门和制动. 因此，采集车辆速度误差、当前油门和制动状态、油门和制动的输入等信息，由切换控制器决策两者输出. 如表2 所示，以ev的取值范围为判断标准将输出方案分为减速区域、保持区域、加速区域. 当前状态分为油门激活（throttle activation，TA）、制动激活（brake activation，BA）、油门和制动均为未激活（not activation，NA），输出方案分为油门控制（throttle control，TC）、制动控制（brake control，BC）、无操作（not operation，NO）.

表2 切换控制策略Tab. 2 Switching control strategies

保持区域作用是为避免控制器在油门和制动踏板之间频繁切换，其输出方案始终保持当前状态.以0.01 作为判断当前油门或制动踏板状态的阈值，若油门开度值大于0.01，则油门激活；若两者均未大于0.01，则当前状态为无操作. 切换逻辑伪代码如下.

输入：速度误差ev；油门开度 α ；制动力矩百分比b；油门输入Iα；制动输入Ib

2 试验验证

2.1 试验说明

以MPC 策略[16]为对比试验，在保证MPC 策略和RC-DCS 控制策略均处于最佳工作状态下，设计CACC 系统驾乘舒适性优化控制试验. 试验采用PreScan 和MATLAB/Simulink 联合仿真，建立由搭载CACC 系统车辆组成的车队，车辆间借助V2X传感器实现专用短程通信（dedicated short range communication，DSRC）功能获取周围车辆行车信息，利用技术自主传感器（technology independent sensor，TIS）模拟激光雷达获取前车距离、相对车速、方位角，若前方车辆为MV，后车退化为ACC 车辆，通过激光雷达进行巡航控制. 为保证控制策略在直道和弯道的适用性，后车跟随MV 时根据自身横摆角速度判断是否行驶在弯道路段，融合长距和短距雷达获取的前车数据，以达到稳定跟踪MV 的目的.

2.2 试验结果及分析

图3 为跟随MV 工况下5 辆CACC 车辆跟车间距误差、速度、加速度对比曲线. 图（a）、（d）中：1—2 号车表示第1 辆车和第2 辆车间的跟车间距，其余类推.

图3 车队整体运行结果对比Fig. 3 Result comparison of fleet overall operation

由图3 可知：MPC 策略最大跟车间距误差1.56 m、最大加速度1.93 m/s2；相同工况下，RC-DCS 策略最大跟车间距误差0.43 m、最大加速度1.45 m/s2，实现CACC 系统精准跟车控制. 相较于MPC 策略，RC-DCS 跟车间距误差、最大加速度分别降低72.44%、24.87%，且曲线波动幅度更小. 可见，RC-DCS 参数波动较小，在CACC 车队的总体运行效率更佳，具有更为稳定、舒适的驾乘体验.

为进一步验证RC-DCS 策略在MV 插入CACC车队工况的整体行驶效果，设计包含10 辆CACC车辆的车队，MV 在50 s 时从3 号车后方切入，试验结果如图4 所示.

由图4（a）看出：相较于MPC 策略，由于RCDCS 策略采用可变车头时距，MV 切入CACC 车队后，为保证行车舒适性，车队跟车时距由1.2 s 调整为1.6 s，因此车辆的速度波动均有一定程度减小.相应地，由图4（b）看出，相较于MPC 策略，RC-DCS控制下的加速度曲线更加平稳，说明该策略可有效降低因MV 介入导致的车队加速度波动，显著提升CACC 车队的驾乘舒适性.

图4 MV 切入结果对比Fig. 4 Result comparison of MV cut-in

为验证下层控制策略在单车跟车稳定性、驾乘舒适性的效率，选取跟随、紧急制动、MV 由旁车道切入本车道3 个典型工况，结果如图5 所示.

由图5（a）可知：在跟随工况下，相较于MPC 策略，RC-DCS 响应更及时，曲线振幅有一定程度减小，标准差降低9.6%，偏度降低26.5%. 可见，RCDCS 可有效改善加速度突变，提高跟随过程中乘车舒适性.

由图5（b）可知：在制动工况下，相较于MPC 策略，RC-DCS 过滤掉加速度的较小波动，标准差降低10.4%. 说明RC-DCS 在制动过程中的表现更加平稳.

由图5（c）可知：在切入工况下，相较于MPC 策略，RC-DCS 对速度变化响应更加及时，加速时调整时间点更早，调整时长约减少2 s. RC-DCS 最大加速度0.34 m/s2，MPC 策略最大加速度0.82 m/s2，其加速度标准差降低2.9%. 说明RC-DCS 具有更好的安全性、舒适性.

图5 典型工况下单车试验结果对比Fig. 5 Result comparison of single vehicle experiments under typical working conditions

3 结 论

本文以CACC 车辆在混行环境下的驾乘舒适性优化为目的，构建适用于CACC 系统的双层控制策略. 主要工作有：

1） 设计采用两状态空间的上层控制策略，定义代价函数从宏观优化车队的整体稳定性和舒适性；设计采用油门和制动踏板切换逻辑控制器的下层控制策略，从微观优化单车的加速度输出稳定性.

2） 结合仿真试验对提出的RC-DCS 进行验证，结果表明所提策略可有效改善CACC 车队跟车间距波动及加速度波动，且在跟车、紧急制动和切入3 种典型工况下对加速度控制效果明显优于MPC，有效提升驾乘舒适性能.

综上，RC-DCS 可满足仿真场景下驾乘舒适性要求，但受试验条件所限，尚未验证在实车平台的运行效果，后续计划将在实车上进一步开展调试、验证工作，以期提高本策略的实用性.

致谢：扬州市宝应县重点研发计划（BY201908）.