面阵阵元位置及幅相误差有源校正算法
袁春姗,唐济远,要庆生
(昆明船舶设备研究试验中心,云南 昆明 650051)
0 引 言
阵列信号处理是利用空间分散排列的传感器阵列和多通道接收来获取信号信息,达到检测信号和进行参数估计的目的。与传统的单个传感器接收信号的一维信号处理相比,阵列信号处理具有灵活的波束控制、较高的信号增益、较强的干扰抑制能力以及很好的空间分辨能力等多种优点[1]。参数化的阵列测向方法,如最大似然算法[2-3]和子空间类算法[4-5],能够突破“瑞利限”,实现信源波达方向(DOA)的高分辨估计。然而,这是基于阵列模型精确已知的条件下。在实际情况中,阵列模型误差不可避免,即使很小的误差也会导致这些超分辨算法性能的严重下降[6-7]。因此,在使用传感器阵列进行测向之前,阵列校正工作是至关重要的。文献[8]中给出线列阵的简化多阶维纳滤波(SMSWF)阵列校正算法,相对特征分解法和常规数据模型估计算法(EACDM),计算量较小,利于工程实现。
由于平面阵相对于线阵来说,在相同阵元数目的情况下,其尺寸要远小于线阵,因此在工程上有实际意义。该文主要介绍了阵元位置及幅相误差模型,并推导了面阵阵元位置及幅相误差SMSWF快速有源校正算法,最后给出了计算机仿真结果。
1 阵元位置及幅相误差模型
在保证实际应用合理性的条件下,对阵列测向及阵列校正模型作假设:声源为远场平面波,点源,窄带信号,阵列流型矩阵各列线性独立,声波在传播过程中不发生畸变,且满足叠加原理,环境噪声为各项同性的。
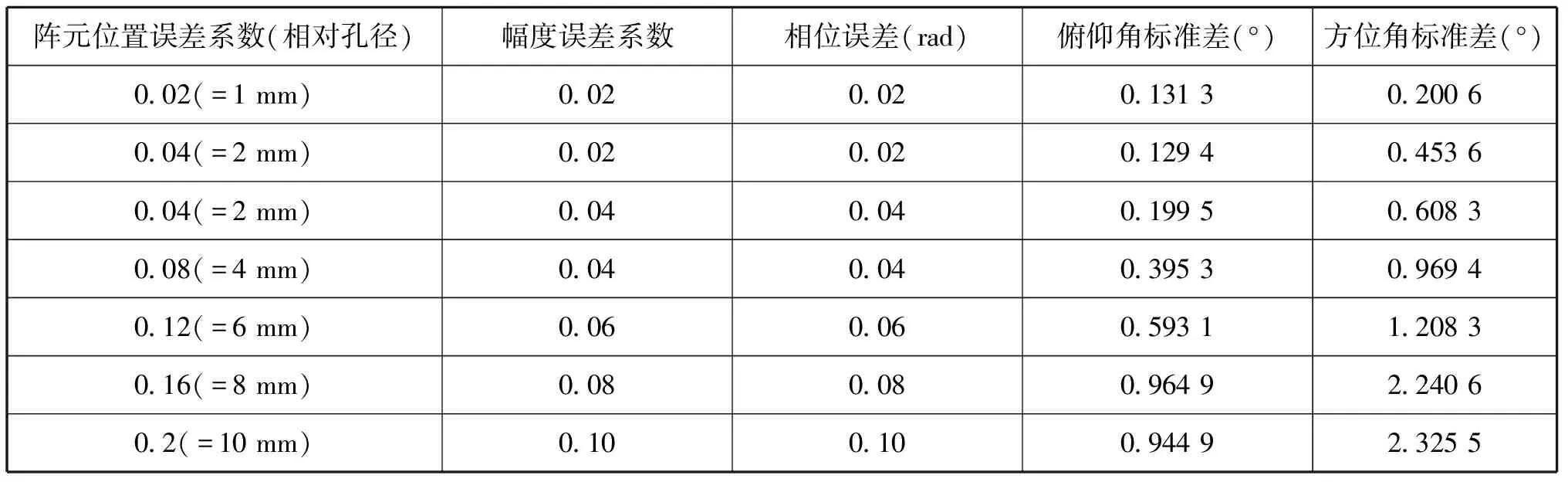
假设有K个中心频率为wc的声源入射到M元空间某阵列(K X(t)=AS(t)+N(t) (1) 式中:X(t)=[x1(t),x2(t),…,xM(t)]T,为M×1维观测信号的数据向量;S(t)=[s1(t),s2(t),…,sK(t)]T为空间信号K×1维向量;N(t)=[n1(t),n2(t),…,nM(t)]T为M×1维噪声数据向量,且噪声与信号互不相关;A为M×K维流型矩阵(导向向量),且有: A=[a(θ1,φ1),a(θ2,φ2),…,a(θK,φK)] (2) 其中,第k个声源的导向向量为: (3) 式中:(xm,ym,zm)为第m个阵元的空间位置;(θk,φk)分别表示第k个声源的方位角与俯仰角。 在实际的工程应用中,传感器阵列往往存在多种阵列误差,这里考虑阵元位置及幅相误差,则实际的阵列输出为: X(t)=ΓΨAS(t)+N(t) (4) Γ=diag(Γ1,Γ2…,ΓM)= diag(g1exp(jφ1),…,gMexp(jφM)) (5) Ψ=[W1⊗ν,W2⊗ν,…,WK⊗ν],ν=[1 1 1]T (6) 式中:Γ为包含幅相误差的M×M维对角矩阵;gm和φm(m=1,2,...,M)分别表示第m个阵元的增益和相位(一般情况下,以第1个阵元为参考阵元,则g1=1,φ1=0);Ψ为阵元位置误差矩阵;Wk=[1 exp(-jwcΔτk2) … exp(-jwcΔτkM)]T为第k个声源的阵元位置误差向量,其中阵元位置误差Δτ为: Δymsinθksinφk+Δzmcosφk) (7) 综合考虑阵元位置及幅相误差,阵列流型可看出是以阵元位置参数及幅相参数为参量而以入射角参数为变量的函数。参数化方法让原本复杂的问题简单化,大大减小了校正的工作量。 针对传感器阵列幅相误差及阵元位置误差有源校正问题,文献[8]提出了线列阵快速误差校正的SMSWF算法。该算法可以同时利用校正源的方位和波形信息来实现阵列误差的参数估计,无需协方差矩阵计算和特征值分解过程,计算量较小,且阵列误差参数估计性能较优。 X(k)(t)=ΓΨ(k)a(k)Ss(t)+N(k)(t) (8) 则阵列协方差矩阵为: (9) 由于信号波形已知,采用MSWF算法直接求出与信号子空间相对应的归一化多级维纳滤波器系数,即: (10) h(k)的具体形式可表示为: (11) sinθkcosφk+(ym+Δym)sinθksinφk]} (12) (13) 记: (14) 对式(13)取相位可得: (Δxmsinθkcosφk+Δymsinθksinφk) (15) 则可得到: (16) 为方便推导,上式改写为: (17) 设ΔΘ(k,1)=Θ(k)-Θ(1),k=2,3,则可得到: (18) 显然,联立方程组可解出阵元位置误差[ΔX,ΔY]。 上式也可改写为矩阵形式: (19) ΔΘ=[ΔΘ(2,1)ΔΘ(3,1)… ΔΘ(K,1)] (20) θcs= (21) 式中:ΔΘ为测量值;θcs为已知值,可解得ΔX和ΔY。 根据最小二乘原则,可得阵元位置误差参数的估计值为: (22) (23) 可得阵元增益参数的估计值为: (24) 至此,分别估计出了阵列阵元位置及幅相误差。 在仿真实验中,假设平面阵以d=λ/2等间距布放,信号频率15 kHz,阵元孔径0.05 m,阵元个数为25,目标俯仰角20°,方位角为30°,信噪比30 dB,快拍数100,阵元位置、增益、相位误差系数服从误差范围内的随机分布。仿真结果如图1、图2所示。 图1 不同误差下指向性函数二维直角坐标系和极坐标系图 图2 不同误差时的MUSIC空间谱 仿真结果显示,随着误差的增大,MUSIC 谱峰的尖锐程度及分辨力随之下降,谱峰偏移程度也不断增加,从而造成信号 DOA 估计误差增大,定位精度降低。对几种误差条件分别做50次蒙特卡洛试验,得到DOA定位精度如表1所示。 表1 不同误差条件下DOA定位精度 随着误差的增大,精度越来越低。因此,在工程中,降低阵列误差的影响,阵列误差校正至关重要。 设定一校正声源分别放置在3个不同的位置发射信号,这3个位置的俯仰角分别为10°,20°,30°,方位角分别为10°,40°和70°,设除参考阵元外的其余阵元位置、增益、相位误差系数服从误差范围内的随机分布。阵元位置x和y轴方向的误差范围(-0.2λ,0.2λ),阵列增益误差为10%,相位误差0.5 rad。采用面阵阵元位置及幅相误差SMSWF校正算法,对阵列进行校准,并且以俯仰角为30°、方位角为70°的校正源为目标。校正前后目标DOA估计结果如图3所示。 图3 阵元位置及幅相误差校正前后DOA估计结果显示 校正前由于阵元位置及幅相误差较大,DOA定位误差较大,校正后谱峰明显尖锐,定位结果准确。50次蒙特卡洛试验得到俯仰角和方位角的标准差如表2所示。通过校正,阵元位置及幅相误差明显减小,DOA估计结果准确,定位误差较小。 表2 不同误差条件下DOA定位精度(标准差) 针对实际工程应用中面阵出现的阵元及幅相误差,旨在找到一种参数估计性能良好、计算量小的算法。根据现有的线阵阵元及幅相误差SMSWF有源校正算法,推导出应用面阵可用的有源校正算法。仿真结果显示,采用面阵阵元及幅相误差SMSWF有源校正算法进行阵列误差校正,可以准确估计误差,提高DOA估计精度。
2 面阵阵元位置及幅相误差SMSWF有源校正算法
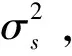
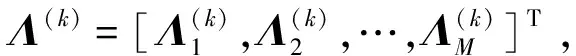

3 仿真分析




4 结束语

