基于多值关联规则的编队作战案例调整方法研究

孟庆林，陈 健，毛建舟

(海军大连舰艇学院，辽宁 大连 116018)

0 引 言

目前，案例推理技术已经逐步应用于舰艇编队作战决策系统设计，它能够很好地处理海上作战指挥过程中的不良结构决策问题，为舰艇编队作战决策提供了新思路。但是，将历史案例直接应用于决策问题时还存在不适宜的情况，如何将案例检索中相似度不高的案例调整为适合当前态势的决策是案例调整的关键。目前，案例调整的主要方法分为3种：(1)基于统计型的调整方法[1]，存在调整能力有限，误差过大的问题；(2)案例推理和规则推理相结合的调整方法[2-3]，大量规则由领域专家制定，存在不够客观、规则库庞大等问题；(3)基于机器学习的调整方法[4-6]，样本需求大、计算量大，且仅能处理数值型数据。鉴于海上编队作战决策具有态势属性多、数据类型丰富的特点，使用以上方法不能很好地解决编队作战案例的调整问题。

本文运用数据挖掘中多值关联规则算法挖掘作战案例中的潜在知识，建立相应的关联规则库，根据编队作战特点制定消解冲突规则的方法，解决了案例调整时的规则冲突问题，避免了领域专家设置决策规则偏主观、工程量大的问题，也弥补了机器学习类方法仅能调整数值型数据的局限。通过仿真实验，证明该方法是有效的。

1 编队作战案例表示

案例表示是案例推理的基础，编队作战案例形式如表1所示，{C1,C2,…,Ch}为历史案例库，Co为目标案例，也即待决策的问题；P={P1,P2,…,Pn}，为编队作战案例的态势属性；S={S1,S2,…,Sm}为编队作战案例的决策属性。Ci={P,S}={xi1,xi2,…,xin;yi1,yi2,…,yim}表示某一个完整的作战案例，xin为第i个案例中第n个态势属性，yim为第i个案例中第m个决策属性，xin、yim可以是具体属性值也可以是具体属性的分类。态势属性主要为舰艇类型、舰艇数量、编队类型，决策属性主要为编队前出接敌的展开方式、攻击目标、编队发射导弹数量等。

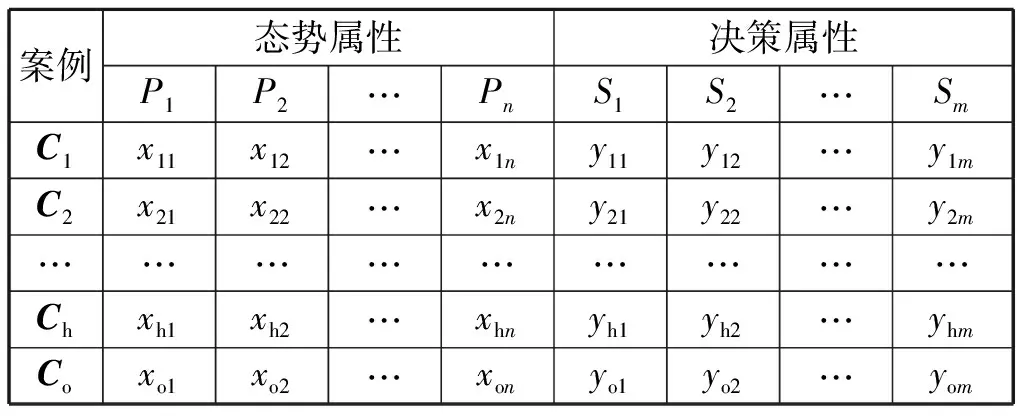
表1 编队作战案例

2 多值关联规则算法挖掘编队作战案例的潜在知识

关联规则是数据挖掘中的经典算法，它能很好地发现数据之间的潜在关系。如果能挖掘编队作战案例中态势属性和决策属性之间的关系，就能利用挖掘的知识为编队作战决策提供依据，同时也可用于调整编队作战案例。

2.1 关联规则的基本模型

R.Agrawal提出关联规则并创立了经典的Apriori算法[7]，为数据挖掘奠定了理论基础。

关联规则的核心是从大量非相关数据中挖掘数据中的潜在知识，它是逐步扫描满足支持度和置信度阈值的迭代算法。其主要分为2步：(1)通过扫描、计算、产生频繁项集、连接及剪枝等步骤产生候选项集，进而寻找所需的频繁项集，重复上述步骤，直到不能产生更大的频繁项集为止；(2)产生关联规则结果，对于每个频繁项集，计算其置信度，输出大于最小置信度阈值的关联规则。

关联规则的逻辑形式为X⟹Y。

支持度为属性X在数据库中出现的频率：

Dsupport(X)=P(X)

(1)

置信度(信任度)为属性Y在属性X的条件下出现的频率：

(2)

提升度用于判断挖掘的规则是否有用，大于1时，认为关联规则X⟹Y可信度较高：

(3)

2.2 改进的多值关联规则

多值关联规则(Q-Apriori)是在Apriori算法上的延伸，由于Apriori算法主要用于挖掘布尔型关联规则[8]，对于数据集中每种属性含有不同数值时，Apriori算法则无法处理，一般会将多值数据转换为布尔型数据，再使用Apriori算法。在编队作战案例中，每种态势属性可能有不同的值，显然是多值数据，如果将多值数据转换为布尔型数据，势必会导致频繁项集的数量呈指数增加，进而加大计算量。因此，重点是将多值关联规则改进为适合编队作战的案例。

在编队作战案例中，多值数据存在明显的从属关系、因果关系，并且绝大多数属性值不大于5、分类属性可列举且不大于10，例如编队中同种军舰的数量、编队的类型。基于上述特点，无需将多值数据转换为布尔型数据，而是在Apriori算法的基础上，通过优化确定频繁项集的剪枝环节，减少大量非必要的运算，实现挖掘多值数据之间的关联规则。

在挖掘关联规则时，会形成大量频繁项集，由于相同属性的不同数值构成的频繁项集无意义、只含有条件属性或者决策属性的频繁项集也无意义，所以在剪枝环节中删除上述可能的候选频繁项集，减少生成频繁项集的数量，避免无用的运算。例如候选频繁项集：{驱逐舰-2，驱逐舰-1，导弹发射-8}，因同一候选频繁项集中，同种属性包含了不同值，在案例中不可能存在，它是支持度为0的无效候选集，应删除。

此外，由于导弹发射数量比较离散，不利于挖掘{态势属性}⟹{导弹发射数量}的关联规则，因此，需将导弹发射数量(决策属性)进行等距转换，从而挖掘到更加全面的关联规则。等距转换公式为：

(4)

改进的多值关联规则算法流程如图1所示。

图1 多值关联规则流程图

3 编队作战案例的调整方法

编队作战案例调整分为3步，如图2所示。(1)编队作战案例库中挖掘关联规则(第2节)，建立相应的规则库；(2)依据当前态势，检索案例库，得到最相似的案例，判断相似度是否大于阈值，大于阈值时，直接使用检索的案例作为当前态势的解决方案；小于阈值时，进入案例调整阶段；(3)依据当前态势遍历已挖掘的规则库，将与当前态势相匹配的规则用以调整案例，当匹配的规则存在冲突时，根据编队作战特点制定相应的消解方法，从而解决了规则冲突问题，保障案例调整的可靠性。关联规则对案例的调整原则：和当前态势相匹配的规则生成相应的决策，将该决策替换原案例中相应的决策，对原案例中未调整的部分保留。

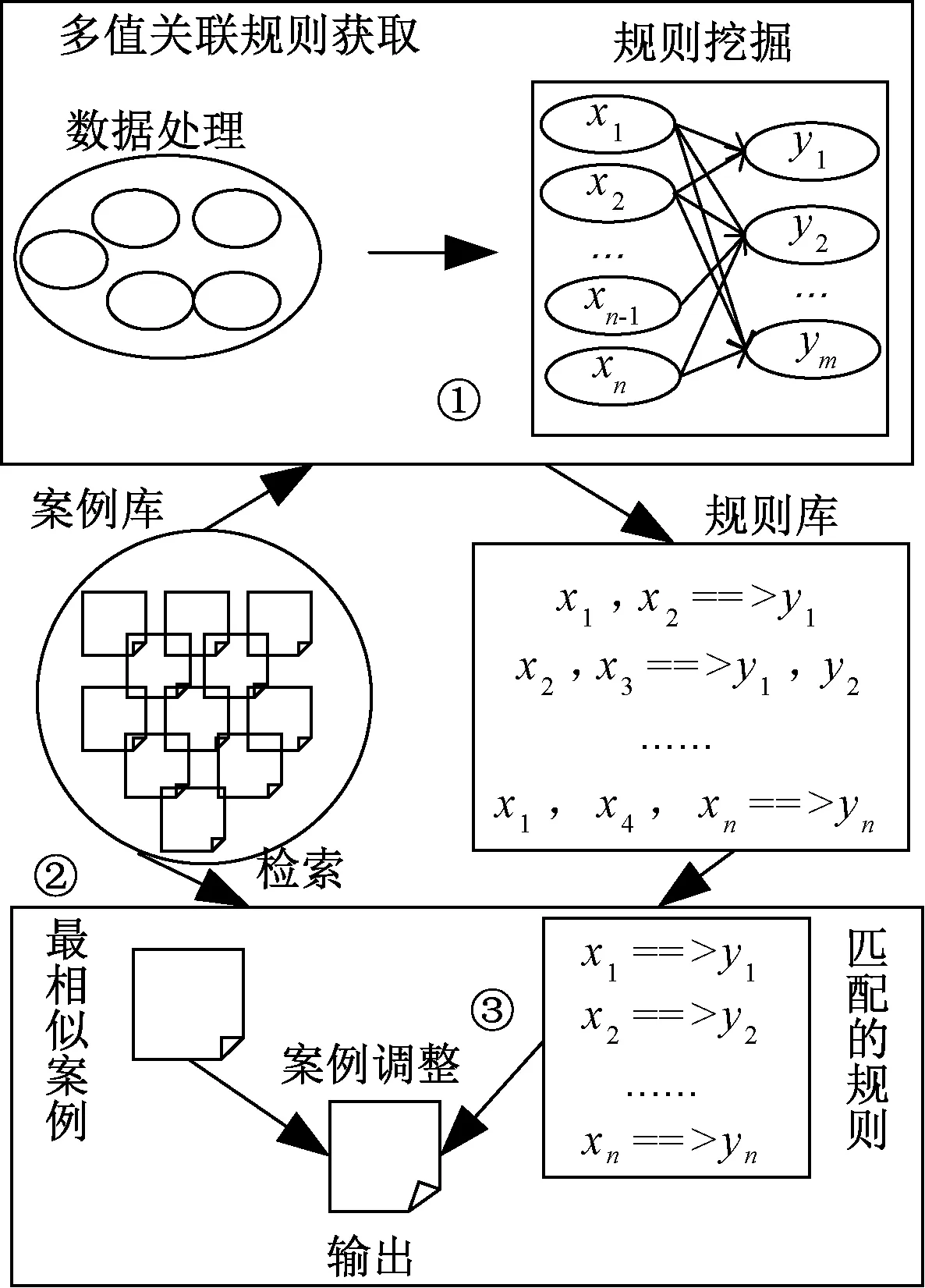
图2 案例调整过程

3.1 获取最相似案例

基于案例推理的编队作战决策，首先就是案例检索，案例检索的阈值为0.9，保证能够检索到足够相似的案例，单个属性的相似度计算公式为：

(5)

式中：xhi为第h个案例中的i个属性值;xoi为当前态势的i个属性值。

全局相似度计算公式为:

(6)

式中：Ch,Co分别表示历史案例和目标案例；wi为对应特征属性的权重，和为1；Ds(Ch,Co)为全局相似度，值越大，案例相似度越高。

3.2 冲突关联规则的消解

在利用挖掘的关联规则制定决策时，关联规则之间可能存在冲突，使得无法制定有效的决策。为了保障决策的可靠性，需要进一步消解规则之间的冲突。

3.2.1 关联规则冲突情况

同种决策属性存在决策的具体值不同的情况，这就造成了规则冲突，例如:

规则1表示决策属性D1属性值为1，规则2表示决策属性D1属性值为2。当条件同时满足规则1和规则2时，结果却产生了冲突。为了保证决策的可靠性，制定了符合编队作战决策的冲突规则消解方法。

3.2.2 冲突关联规则的具体解决方法

在海上编队作战时，遵守一个战斗原则：集中核心力量消灭敌方核心兵力部署。此外，研究发现我方兵力与兵力展开类型呈正相关，敌方兵力与我方决定的攻击目标和导弹发射数量呈正相关。基于上述2点原因，现做出消解冲突规则的方法。

方法1：关联规则的优先级与规则中态势属性的作战力量优先级相对应(海上作战力量的排序：航母>驱逐舰>护卫舰>导弹艇>作战支援舰)。例如存在A1>A2>A3的优先级顺序，则3.2.1小节中的冲突规则就可以确定使用规则1，弃用规则2。

方法2：用含我方兵力态势属性的规则推导我方兵力展开类型，用含敌方兵力态势属性的规则推导发射导弹数量和攻击目标，并且是多属性推导单个决策。

4 仿真实验

本文选取了35个编队作战案例，其中30个案例用于挖掘关联规则，另5个用于测试案例调整的精度。如表2所示，其中字母表示态势属性，数值表示相应属性的数量或属性的类型。

表2 舰艇编队作战案例

我方兵力：A：航母，B：驱逐舰，C：护卫舰，D：导弹艇，E：作战支援舰，F：直升机。

敌方兵力：a：航母，b：驱逐舰，c：护卫舰，d：导弹艇，e：作战支援舰，f：直升机，h：编队类型。

舰艇编队类型可分为单横队、单纵队、V字队形、左右梯形、交错队形、楔形队形，表中分别用1、2、3、4、5、6表示。

决策属性：Q：集群1，q：集群2，G：集群1导弹攻击，g：集群2导弹攻击，M：攻击目标。

编队在海上对敌攻击时，一般分为2个集群兵力展开。可以按照1：航-驱(航母-驱逐舰为主的集群兵力展开)、2：航-护、3：航-导、4：航-作、5：驱-护、6：驱-导、7：驱-作、8：护-导、9：护-作、10：导-作为主的集群进行兵力展开。

攻击目标通常选择敌方核心力量，这里用相应的数字代替，1：航母，2：驱逐舰，3：护卫舰，4：航-驱(航母和驱逐舰)，5：航-护，6：驱-护，7：航-驱-护，8：驱-驱，9：护-护。

对海武器：YJ-18反舰导弹和YJ-83反舰导弹，每个集群的载弹量肯定能支撑一场战斗。对海攻击采用饱和式打击方式，只需1枚导弹命中目标，对目标也能造成毁灭性的打击。

4.1 编队作战案例调整

为了从案例库中挖掘相对全面的规则，经过反复实验后，将Q-Apriori程序中的最小支持度设置为0.133(4/30)、最小置信度为0.5，得到的关联规则效果最好。

为了使读者更好地明白本文案例调整的原理，本文给出了测试案例③的调整过程和结果。

通过案例检索得到最相似的案例为16，相似度仅为0.835 2，低于相似度阈值0.9，所以历史案例16的作战方案不能直接使用，需要对作战方案进行调整。

用测试案例③的态势属性遍历规则库，可以得到如表3所示的关联规则。

表3 与态势匹配的关联规则

根据3.2节冲突规则的消解方法，可以生成的决策为Q2(集群1：航母-护卫舰为主)、q5(集群2：驱逐舰-护卫舰为主)、G9(集群1发射导弹数量：9枚)、g9(集群2发射导弹数量：9枚)、M8(攻击目标：驱逐舰-驱逐舰)。将生成的决策替换历史案例16的决策，案例调整完成，调整前后的结果对比如表4所示。对比测试案例③，经过调整后的决策方案和测试案例的决策方案非常接近，证明此方法对编队作战案例调整有效。

表4 案例调整前后对比

最后将调整后的案例用于实际决策，指挥决策内容如表5所示。表中的海区和各阶段时刻需要根据实际情况制定。

表5 编队作战决策

4.2 案例调整精度分析

为了衡量本文方法的调整精度，引入平均绝对误差百分比(MAPE)，计算数值型数据的调整精度:

(7)

针对非数值型数据，定义如下计算精度的公式：

(8)

总体调整精度公式：

(9)

由上述5个测试案例，再利用本文所提的案例调整方法和调整精度公式绘制了5个测试案例的调整精度图，如图3所示。由图3可知，案例的调整精度可以保持在0.8左右，调整精度相对较高。

图3 调整精度

5 结束语

本文采用多值关联规则的方法挖掘编队作战案例中的潜在知识，用关联规则去调整案例，并解决了案例调整时的规则冲突问题，保证了案例调整精度。通过仿真实验，证明该方法对海上编队作战案例的调整有效。如果经过案例调整后的决策还不能满足指挥员的要求，那就需要指挥员凭借自身作战经验进行调整，制定决策。