基于跟踪微分器的捷联导引头解耦算法研究
李庆波,方泽远,陈国良,梅志伟,杨 婷
(上海机电工程研究所,上海 201109)
0 引 言
在导弹精确寻的制导过程中,导引头完成对目标的自主搜索、识别和跟踪,并给出制导控制所需的视线角速率等信息,确保导弹精确命中目标。导引头是精确制导武器的重要核心部件,并在很大程度上决定了制导武器的打击精度与成本[1]。
根据结构形式不同,导引头可以分为框架式导引头与捷联式导引头。传统框架式导引头具有较大总视场角,能够快速捕获并精确跟踪目标,输出制导所需的视线角速率信息,但也存在价格高昂、结构复杂、可靠性低等缺点[2]。
相比于框架式导引头,全捷联导引头主要由固定视场光学系统、探测器及信号处理系统组成,与弹体捷联安装,具有体积小、质量轻、复杂性低、可靠性高、瞬时视场大、视线角速率不受限制及成本低等诸多优点。但捷联成像导引头的测量信号中耦合有弹体姿态运动信息,因此,需要设计合适的解耦算法以实现弹体姿态运动的解耦[3],从而获得视线角速率。
文献[4-8]均通过建立视线角速率提取的状态方程和量测方程,使用卡尔曼滤波的方法实现视线角速率的提取。但卡尔曼滤波方法中使用的状态方程是对非线性弹目运动模型的近似表达,而量测方程又极为复杂,涉及到的变量和运算较多,因此工程应用中面临许多困难。
为了从被噪声污染的信号中提取微分信号,韩京清[9]于1994年提出了跟踪微分器的解决方案。而跟踪微分器作为一种非线性估计方法,能够较好地解决从不连续或带随机噪声的测量信号中合理跟踪提取连续信号及微分信号的问题[10-12]。文献[13]利用跟踪微分器研究了视线角加速度的滤波算法。王佩[14]设计了最速离散跟踪微分器、滑模微分器与非线性微分器等3 种微分器估计视线角速率,但并未给出具体的跟踪微分器参数整定方法。
本文拟从频域的角度,对跟踪微分器的特性进行分析研究,并针对解耦问题展开具体设计和参数整定。
1 视线角速率提取的数学原理
1.1 坐标系定义及视线角求解
捷联导引头实时获得目标在弹体系下的离轴角,弹上惯测系统可测量获得弹体的实时飞行姿态,按照图1 所示的坐标转换关系,可求解获得以导弹为原点的惯性系下的视线角。
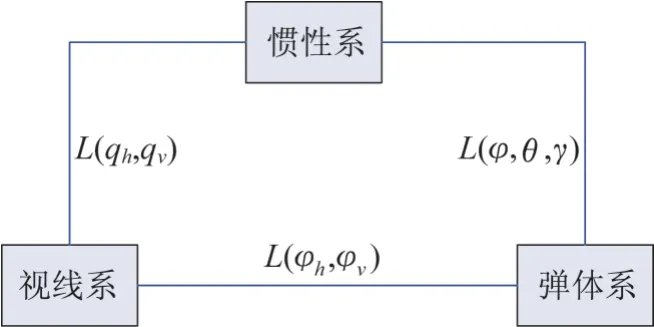
图1 坐标系转换关系Fig.1 Coordinate system transformation relation
图中:qv、qh分别为惯性系下的高低视线角和方位视线角;φv、φh为目标在弹体系下的高低离轴角和方位离轴角;φ、θ、γ为弹体偏航角、俯仰角和滚转角;L(x,y,z)表示坐标系间的转换矩阵,内部参数为从x开始依次转换的角度。
设弹目相对距离为R,则在视线系下的目标位置坐标为[R0 0]′,根据坐标关系转换,满足以下等式:

令

对式(1)展开后可得

由此可求解获得惯性系下的视线角为
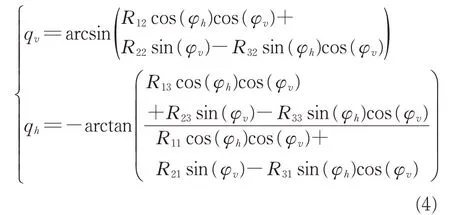
理论上对以上信号进行微分,即可获得视线角速度。但在工程实际中,直接微分获得的视线角速度噪声非常大,将其应用于导弹制导回路当中会造成较大的脱靶量。
1.2 跟踪微分器提取视线角速率
跟踪微分器利用了数值积分优于数值微分的事实,将给定信号的微分转化为对一组微分方程的积分问题,可实现任意信号的跟踪及微分。跟踪微分器的输入输出关系如图2所示。

图2 跟踪微分器输入输出关系Fig.2 Tracking differentiator I/O relationship
图中:ν为输入信号;ν1为对输入信号的跟踪输出信号;ν2为基于输入信号提取获得的微分信号。
2 典型微分器分析
按照跟踪微分器的输入输出关系可知,将式(4)解算获得的含有噪声的视线角信号作为输入信号,通过设计合适的跟踪微分器,可获得制导需用的视线角速度信号。
自跟踪微分器诞生以来,已出现了多种形式,并获得了广泛应用。本文选用以下两类典型的跟踪微分器,研究其在视线角速率提取中的设计与应用问题。
2.1 最速跟踪微分器
最速跟踪微分器的形式如下:
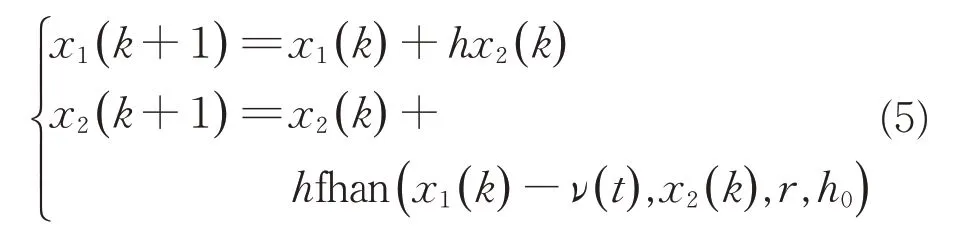
式中:ν为输入信号;x1为ν的跟踪信号;x2为ν的微分信号;h为积分步长;r影响跟踪速度;h0影响滤波效果。
fhan(x1,x2,r,h0)函数为

2.2 非线性跟踪微分器
非线性跟踪微分器的形式如下:

其中:

式中:R、α、β、δ为需设计的参数;R、α影响跟踪速度;β影响滤波效果;δ影响线性区范围,有利于消除原点附近的颤振。
3 基于频域的跟踪微分器参数设计与性能分析
从式(4)可知,惯性系视线角速度提取中,主要与陀螺敏感的姿态角速度信号和导引头的测角信号密切相关。因此陀螺噪声、陀螺带宽及导引头测量噪声等都会影响视线角及视线角速度的输出。
陀螺带宽决定了其角速率敏感的频谱范围,对于高于陀螺带宽的弹体高频振动信号,由于不能被准确敏感而导致无法实现理论上的解耦,因此对式(4)中存在的高于陀螺带宽的信号,需将其尽可能地衰减。
陀螺测量信号的噪声和导引头测量噪声可视为白噪声,该类噪声分布于全频谱范围内,由于低频部分与制导需要的有效信号接近甚至重合,难以被大幅衰减。因此若能对低频部分快速跟踪,对高频部分有效衰减,则既能保证视线角速度提取算法具有较小的时间常数,又具备较高的提取精度。
基于以上考虑,本文拟利用频域特性计算与分析,开展跟踪微分器的参数设计,以获得较好的视线角速率提取效果。
3.1 基于等效合力的跟踪微分器频域特性计算方法
在经典控制领域,线性环节的频域特性可通过公式推导直接计算获得,而非线性环节的频域特性则不易获得,这为跟踪微分器的设计带来一定的困难。
在旋转导弹控制中,常用到等效合力的方式来设计和确定导弹的控制力方向及控制力大小[15]。本文借鉴等效合力的计算方法来实现对跟踪微分器频率特性的快速近似计算,便于开展具体的参数设计。利用等效合力获取滤波器频率特性的数学原理如下。
为计算跟踪微分器对频率为f的信号的滤波效果,给定如下的标准输入信号:

设滤波器的输出信号为vout,则在每一个周期T内,执行以下运算:

则滤波器在频率f条件下的幅值增益为
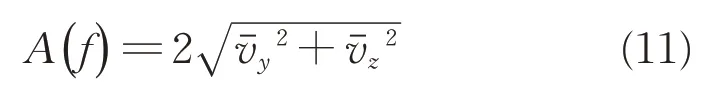
滤波器在频率f条件下的相位变化为

按照以上算法,即可求得不同频率条件下滤波器的幅值增益和相位变化,从而可获得滤波器的频域特性,这为滤波器的参数设计和性能评估提供了有利的设计支撑。
3.2 跟踪微分器参数整定及特性对比
本节主要利用频谱特性计算,结合时域信号响应特性,设计合适的解耦滤波器参数。滤波器的设计应保证对低频信号的准确跟踪和对高频信号的大幅衰减,同时也要保证较快的跟踪速度。基于以上的设计原则,开展最速跟踪微分器和非线性跟踪微分器的参数设计。
3.2.1 最速跟踪微分器的频率特性
最速微分跟踪器是在最大加速度r限制条件下,保证输出信号对输入信号的最速跟踪。但在设计值r一定的条件下,通过扫频获得的最速跟踪微分器的频域特性会受到输入信号幅值的影响。
当r取固定值8时,不同扫频幅值信号获得的频域特性对比如图3~4所示。

图3 最速跟踪器频域特性曲线Fig.3 Frequency domain characteristic curve of fastest tracker

图4 最速微分器频域特性曲线Fig.4 Frequency domain characteristic curve of fastest differentiator
图中的A表示输入扫频信号的幅值。从图中可以看出,最速跟踪微分器的频域特性随扫频输入信号的变化而发生变化,其原因是最速跟踪微分器只能以最大加速度r对信号进行跟踪。当输入信号的幅值变大时,跟踪的时间就会变长,表现在频域上则为带宽变窄,相位滞后增加。
在视线角速率提取的问题中,输入信号的幅值是随弹目相对运动关系的变化而动态变化的,因此最速跟踪微分器提取视线角速率并不合适。
3.2.2 非线性跟踪微分器的频率特性
非线性跟踪微分器的可调参数较多,通过对其频域特性的判断,同时结合导引头视线角速率提取的具体要求,整定的一组参数为:R=100,α=0.8,β=5,δ=0.001。
其频域特性曲线如图5~6所示。
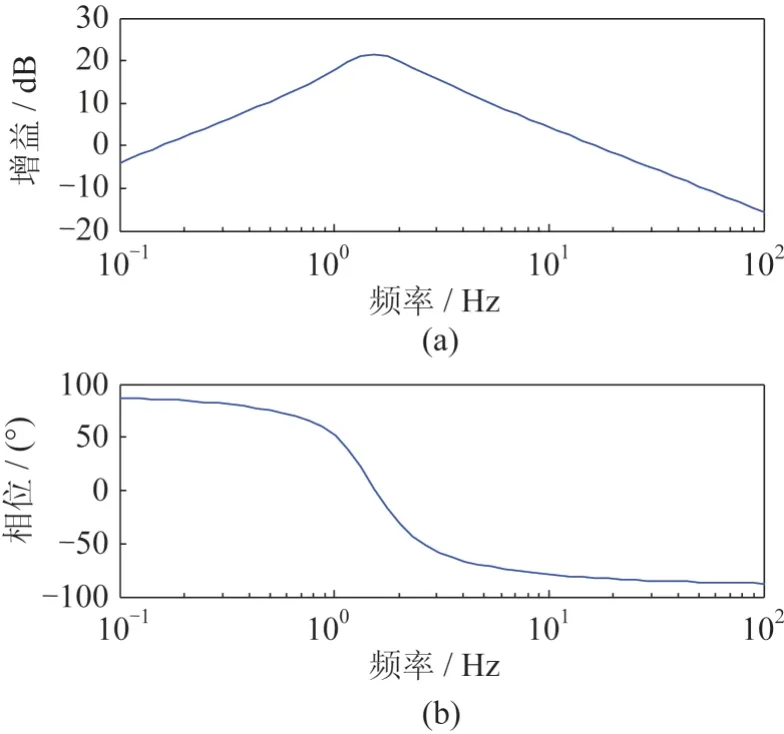
图5 非线性跟踪器频域特性曲线Fig.5 Frequency domain characteristic curve of nonlinear tracker
由图5 中的曲线可知,跟踪部分在低频段非线性跟踪微分器能够较好地复现输入信号,在高频段能够达到对输入信号的快速衰减。由图6 中的曲线可知,微分部分在低频段对信号实现微分功能,在高频段同样实现快速衰减。因此该组参数能够达到较好的跟踪和微分效果。

图6 非线性微分器频域特性曲线Fig.6 Frequency domain characteristic curve of nonlinear differentiator
4 滤波效果对比
4.1 仿真建模
本节通过建模仿真,对比不同滤波器条件下视线角速度的提取精度。视线角速度解耦仿真模型中涉及的内容包含:导引头理论测角、理论弹体姿态运动、导引头探测模型、陀螺模型、陀螺噪声及导引头测角误差等。具体仿真条件如下。
4.1.1 理论建模
弹体理论姿态角速度为

式中:弹体姿态角速度ωx、ωy、ωz单位为(°)/s,包含了低、中、高频信号,同时加入了白噪声振动信号Δωx、Δωy、Δωz,白噪声的方差为0.1(°)/s。弹体姿态角理论值由弹体姿态角速度解算获得。
理论视线角速度为
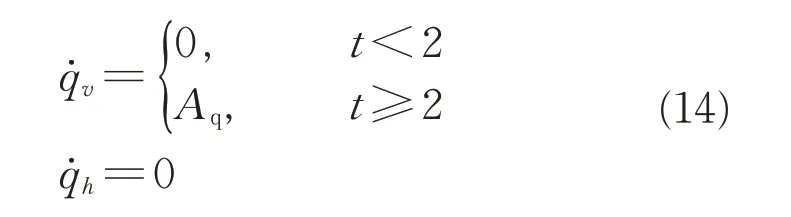
式中:Aq为设计输入值。
基于理论视线角速度,可计算获得惯性系下的理论视线角。
导引头理论测角为
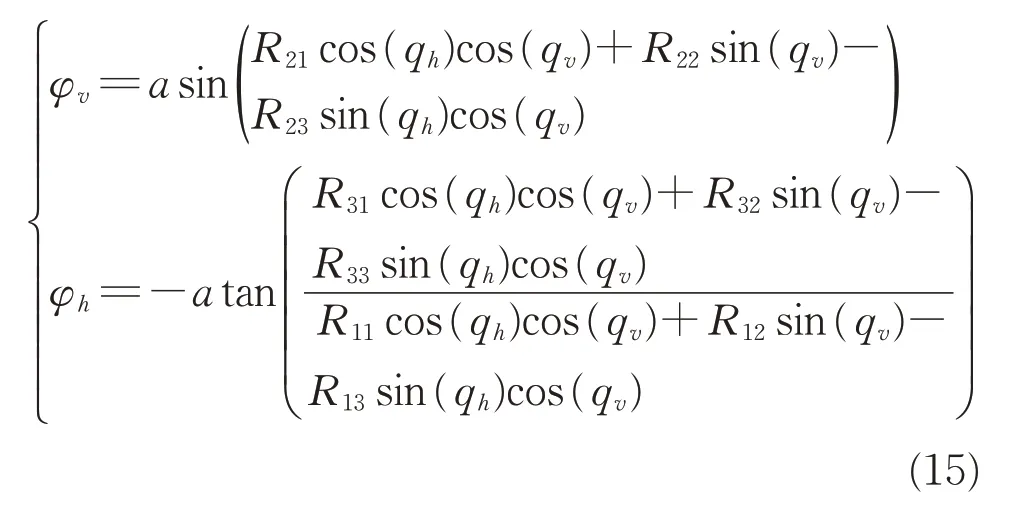
4.1.2 传感器与误差模型
导引头的角度测量处理时间通常为毫秒级,因此本文仅考虑陀螺的测量模型,其传感器模型为

式中:ωtl=150×2π;ξtl=0.6;ktl=1。陀螺噪声信号取为0.1(°)/s(1σ),导引头测角精度为0.1°(1σ)。
4.2 仿真对比
基于第3 章中设计的跟踪微分器,开展视线角速率解耦仿真验证,仿真结果如图7所示。

图7 幅值为1时的解耦曲线对比Fig.7 Comparison of decoupling curves with amplitude of 1
从图7~8 中可以看到,最速跟踪微分器的解耦效果及快速性受输入信号的影响,因此不适用于视线角速度的解耦。非线性跟踪微分器的解耦能力及快速性与输入信号无关,其上升时间(到达90%的时间)约为0.15 s,且能在以上误差条件下实现0.4(°)/s(3σ)的解耦精度。基于频域特性设计的非线性跟踪微分器解耦效果较好且时间常数小,能够较好地解决捷联导引头的解耦问题。

图8 幅值为5时的解耦曲线对比Fig.8 Comparison of decoupling curves with amplitude of 5
5 结束语
本文利用两种典型的跟踪微分器开展捷联导引头视线角速率提取研究,在跟踪微分器的具体设计过程中,提出了基于频域特性开展参数设计的思路,并利用旋转导弹控制当中的等效合力方法解决了非线性环节频域特性提取的问题。基于以上设计思路开展了具体设计及仿真分析对比,仿真结果表明,非线性跟踪微分器具有良好的解耦效果,而最速跟踪微分器的解耦能力由于受到输入信号本身幅值的影响,不宜用于视线角速率的解耦问题当中。

