临近空间太阳能无人机横航向变质心控制技术

王克帆，邱潇颀，高长生，荆武兴

（哈尔滨工业大学航天工程系，黑龙江哈尔滨 150001）

0 引 言

近年来，随着太阳能电池技术的不断发展，临近空间太阳能无人机重新成为世界各国军事研究的热点。由于其具有飞行高度高、工作寿命长、覆盖范围广、使用成本低的特点，因此可以弥补飞机平台高度低、时间短以及卫星平台成本高、侦查密度低的缺点，是执行侦查预警、目标跟踪以及通信等任务的理想空中平台［1-2］。在空天防御领域，临近空间太阳能无人机兼具传统航空航天器的诸多优点，也被称为“高机动性伪卫星”，应用前景广阔。

当前太阳能无人机的横向控制常采用方向舵偏转和螺旋桨差动实现。例如，Meola 等［3］利用方向舵偏转实现了对小型无人机的控制，验证了方向舵控制方案的可行性；赵维娜等［4］基于变权伪逆法和变约束再分配伪逆法，研究了螺旋桨差动控制分配算法。考虑到能源约束的问题，太阳能无人机多采用大展弦比、低结构面密度的设计，以此来提升气动效率、降低结构重量［5］。但这会造成太阳能无人机的机翼扭转刚度不足，再加上其飞行高度较高导致来流密度较小，使得副翼操纵效率低下，甚至会出现“副翼反效”现象［6］。太阳能无人机的蓄电池密度较大、质量相对集中，且其质量通常占全机质量的30%～40%［7］，因此，选用蓄电池作为可移动质量块的变质心能够获得足够的控制力矩［8-9］。

变质心控制技术已经在多个领域中得到了应用。Huang 等［10］基于PID 控制理论，利用变质心技术实现了对太阳帆卫星的高度控制；周革［11］将变质心技术应用于平流层飞艇的姿态控制，分析了飞艇控制能力与滑块质量、位移、移动速度之间的关系。Erturk 等［12-13］将变质心技术应用于固定翼无人机的控制，通过将双滑块放置于无人机的纵轴和横轴，实现了对无人机的稳定控制；此外，在火星探测器［14］、弹头再入［15］、水下航行器［16］等领域，变质心控制技术也有报道。

本文以临近空间目标预警探测为背景，以小型正常式布局太阳能无人机为对象，基于传统的倾斜转弯（bank to turn，BTT）控制，提出了以蓄电池为质量滑块、滑轨沿展向布置的太阳能无人机变质心控制方案，分析了采用此方案的无人机动态特性，并基于PID 控制理论设计了以滑块偏移量为控制量的横向控制器。

1 变质心太阳能无人机动力学特性

1.1 机体坐标系的定义

传统无人机机体坐标系原点定义于飞机质心处。但是对于本文研究的变质心无人机，其质心位置在不断变化。为了避免歧义，需要对本文定义的机体坐标系作出说明：机体坐标系原点位于不包括质量块的机体质心B 处，x轴沿体轴指向飞机头部，y轴垂直于飞机纵向对称面指向飞机右侧，z轴与x、y轴构成右手直角坐标，指向飞机腹部。

1.2 变质心太阳能无人机构型

本文研究的变质心太阳能无人机的基本构型如图1所示。

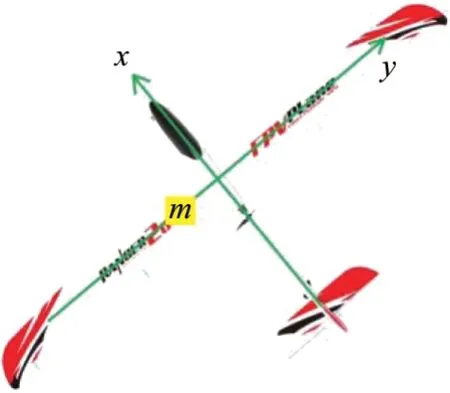
图1 变质心太阳能无人机基本构型Fig.1 Basic configuration of moving-mass solarpowered UAV

设飞机机体质量为mB，滑块质量为m，系统总质量为mS，有

质量比定义如下：

此外，机体质心B 在机体坐标系下位置为(0，0，0)，设系统质心S在机体坐标系下位置为（xS，yS，zS），滑块质心位置在机体坐标系下为（x，y，z）。从而有

式中：RS、RB、r分别为机体坐标系下系统质心、机体质心、滑块质心的位置矢量。进一步有

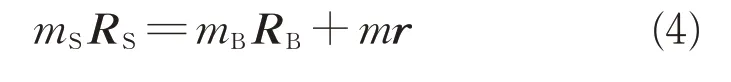
即

1.3 无人机运动方程

1）运动学

经简单的坐标转换，可以得到无人机的运动学方程如下：

式中：pn、pe、pd表示无人机位置矢量在惯性坐标系三轴的分量；u、v、w和p、q、r分别表示飞行速度和转动角速度在机体坐标系三轴的分量；ϕ、θ、ψ分别代表滚转角、俯仰角和偏航角。

2）动力学

对于质心平动动力学，有如下关系：

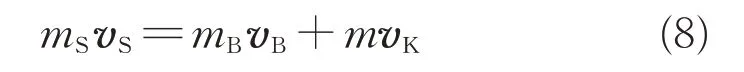
式中：vS、vB、vK分别为系统质心、机体质心和滑块质心的绝对速度。设机体坐标系原点的绝对速度为vo，机体转动角速度为ω，由式（8）可导出：

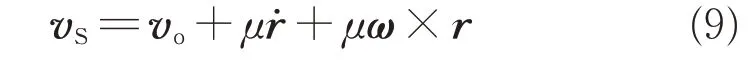
对式（9）进行微分可得

式中：δ为相对速度微分符号；ω为系统的旋转角速度。

在机体坐标系下研究式（10），可得无人机质心平动动力学方程为

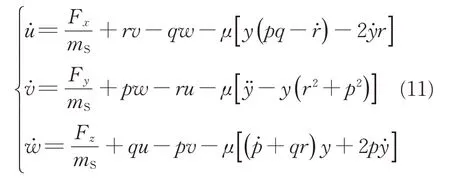
式中：Fx、Fy、Fz为无人机所受外力在机体坐标系各轴分量；y为滑块偏移量。

对于绕质心转动动力学，由动量矩定理有

式中：H为系统的动量矩；M为系统受到的合外力矩。

同样在机体坐标系下处理式（12），可得无人机转动动力学方程为

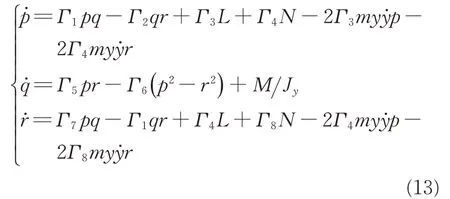
式中：L、M、N为所受外力矩在机体坐标系各轴分量；

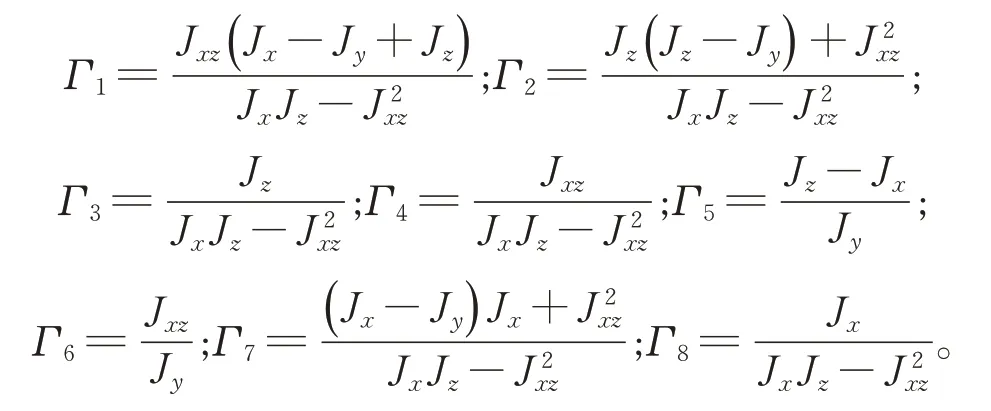
用滑块替代副翼后，式（11）和式（13）中力和力矩的表达式为

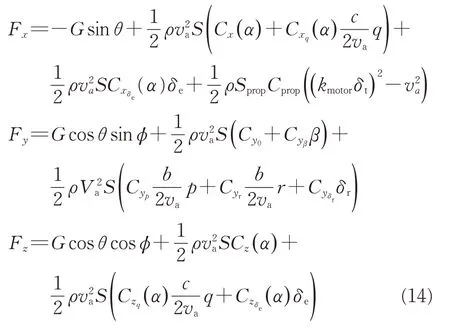
式中：G＝mSg为系统总重量；ρ为大气密度；va为无人机空速；S为机翼参考面积；c为机翼平均气动弦长；α、β为攻角和侧滑角：δe、δr、δt分别为升降舵偏转角、方向舵偏转角和发动机油门大小；Sprop、Cprop是螺旋桨扫过的面积和效率系数；kmotor为与发动机自身属性相关的常数。

式中：b为机翼展长；kΩδt为发动机转动角速度；kT为实验确定的常数。

补充方程：

1.4 线性化模型

基于小扰动假设，在特征点处的横向运动线性化方程为

式中：状态向量x＝[ΔβΔpΔrΔϕΔψ]T；控制输入为u＝[ΔyΔδr]T；状态矩阵A和控制矩阵B的具体形式见式（18）～（19），式中各项参数的具体值见文献［17］。

2 变质心太阳能无人机横向控制系统设计

图2 展示了基于BTT 控制方案设计的变质心太阳能无人机横向控制系统基本结构，由滚转角控制器和偏航角控制器两部分组成。图中，Δψc表示期望偏航角；Δϕc表示期望滚转角。

图2 横向控制系统结构Fig.2 Lateral control system structure

2.1 滚转角控制器

由图2可知滚转角控制器是整个横向控制系统的内回路，因此要求其带宽足够大。同时，为了改善滚转阻尼特性，滚转角控制器选用“比例＋微分（PD）”控制方案，利用可由陀螺仪测量得到的滚转角和滚转角速度作为反馈信号。

式中：Ly、Lp为式（18）和式（19）中的值。

可知滚转角控制器的输出为

2.2 偏航角控制器

由于滚转角控制回路采用PD 控制，为了得到无误差的横向控制系统，偏航角控制器选用“比例＋积分（PI）”的控制形式，其结构如图4所示。由此可知偏航角控制器的输出为

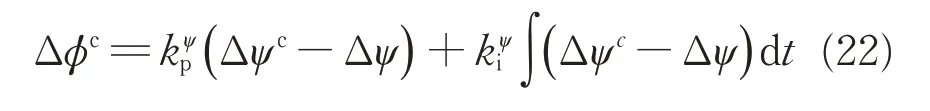
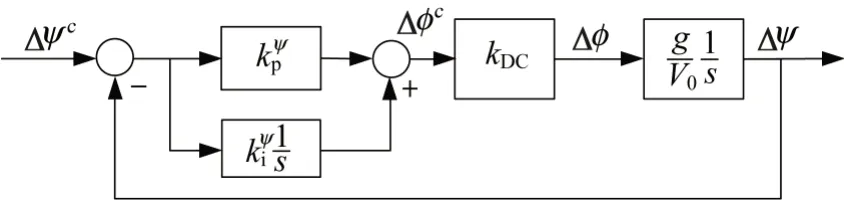
图4 偏航角控制器结构Fig.4 Yaw angle controller structure

在设计中，只要保证偏航角控制器的带宽小于滚转角控制器带宽的1 5，则滚转角控制器的数学模型就能用其稳态增益kDC来表示（kDC＝1），进而可以忽略其动态。

2.3 参数表达式设计

将图3 所示滚转角控制器的闭环传递函数与式（23）所示标准二阶环节对比，可得滚转角控制器参数的表达式分别为式（24）和式（25）。

图3 滚转角控制器结构Fig.3 Roll angle controller structure

当kDC＝1 时，图4 所示偏航角控制器的闭环传递函数为

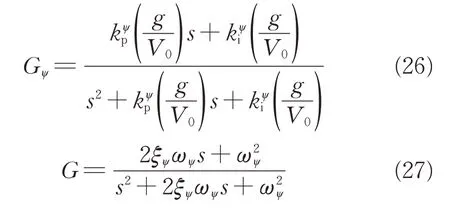
将式（26）与式（27）所示二阶传递函数对比可得偏航角控制器参数如式（28）和式（29）。

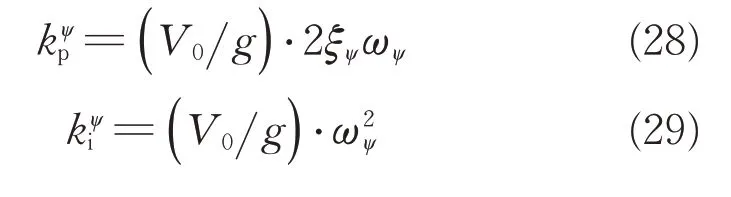
3 仿真分析

为降低太阳能无人机结构复杂性，在仿真中将方向舵偏转角Δδr设置为0，即仅以滑块偏移量Δy作为可控量。考虑到驱动滑块运动的舵机的延迟效应，可将其看作时间常数为0.2 s的惯性环节。此外，滑块的最大滑动速度设置为0.5 m/s，最大滑动行程设置为0.6 m。

无人机的基本几何参数如表1 所示。结合式（24）～（25），选取阻尼比为ξϕ＝1.5，自然振荡角频率为ωϕ＝πrad/s，可得其滚转角控制器参数。为了保证外回路带宽小于内回路带宽的1 5，选取ωψ＝π6 rad/s，选取阻尼比为ξψ＝1.2，结合式（28）～（29），可得其偏航角控制器参数，如表2所示。

表1 变质心太阳能无人机参数Tab.1 Parameters of moving-mass solar-powered UAV

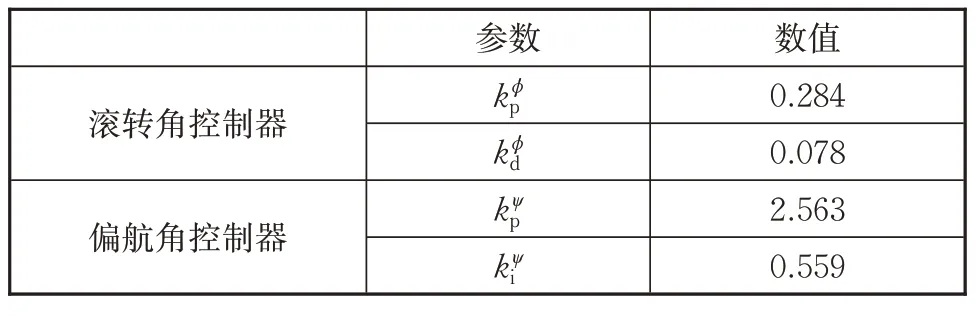
表2 控制器参数Tab.2 Parameters of controller

设置两个仿真条件：Con1为不做任何处理的理想状态；Con2 表示由于阵风的作用，在t＝10 s 和t＝50 s处滚转角存在标准差为5°的随机扰动。

3.1 被控特性分析

基于以上线性化结果，可求得滚转角与滑块偏移量之间的传递函数关系为

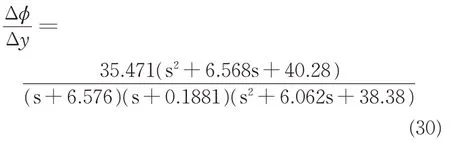
从而可见其极点分布如表3所示。

表3 极点分布Tab.3 Poles distribution

显然传递函数特征根实部均在左半复平面内，可知系统是稳定的，其中滚转模态衰减速度较快，而螺旋模态是一种慢衰减运动。

图5 反映了在滑块质量一定时，分别改变其滑动速度和最大行程时滚转角的响应曲线。由图5（a）可以看到不同滑动速度所产生的滚转角稳态值是相同的，其主要影响动态过程，即滑动速度越快，响应也越迅速，但速度增大到一定程度后，这种现象不再显著。值得注意的是，滑动速度的增加所引起的系统动态特性改变并不明显。而图5（b）反映出最大行程的改变会造成横向操纵能力发生较大范围的改变，显然滑块行程越大，操纵能力就越强。

图5 改变滑块移动速度和行程时的滚转角响应Fig.5 Response of roll angle for different sliding speeds and strokes

3.2 滚转角控制器

图6 展示了滚转角控制器在Con1 和Con2 条件下对滚转角指令的跟踪效果。由图6 可以看出：在理想状态下，滚转角控制器跟踪10°阶跃信号时的调节时间约为3 s，且过渡过程平滑无超调，但是由于采用的是PD 控制律，因此滚转角跟踪会存在一定的稳态误差；当存在阵风干扰导致滚转角出现偏移时，控制器在较短时间内（t＜5 s）便消除了阵风的影响，使系统状态量维持在稳定值，具有较好的抗风性。

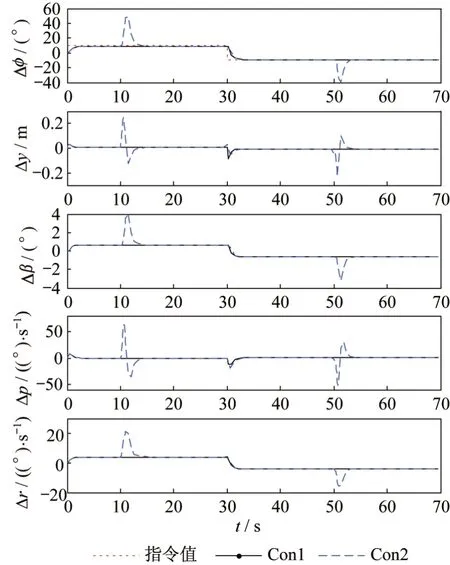
图6 滚转角控制器响应曲线Fig.6 Response curves of roll angle controller

3.3 偏航角控制器

图7 展示了偏航角控制器在Con1 和Con2 条件下对偏航角指令的跟踪效果。由图7 可知：在无阵风扰动情况下，控制器实现了对偏航角指令的无误差稳定跟踪。在偏航角指令产生－70°的阶跃变化时，控制器可以在10 s 内将系统镇定下来，过渡过程存在一定的超调量，超调量的大小与滑块的最大滑动速度和最大滑动距离有关；当存在阵风干扰时，以滚转角控制作为内回路的偏航角控制器同样具有良好的抗风性能，在10 s 之内便可消除阵风的影响，使系统状态稳定到指令值。

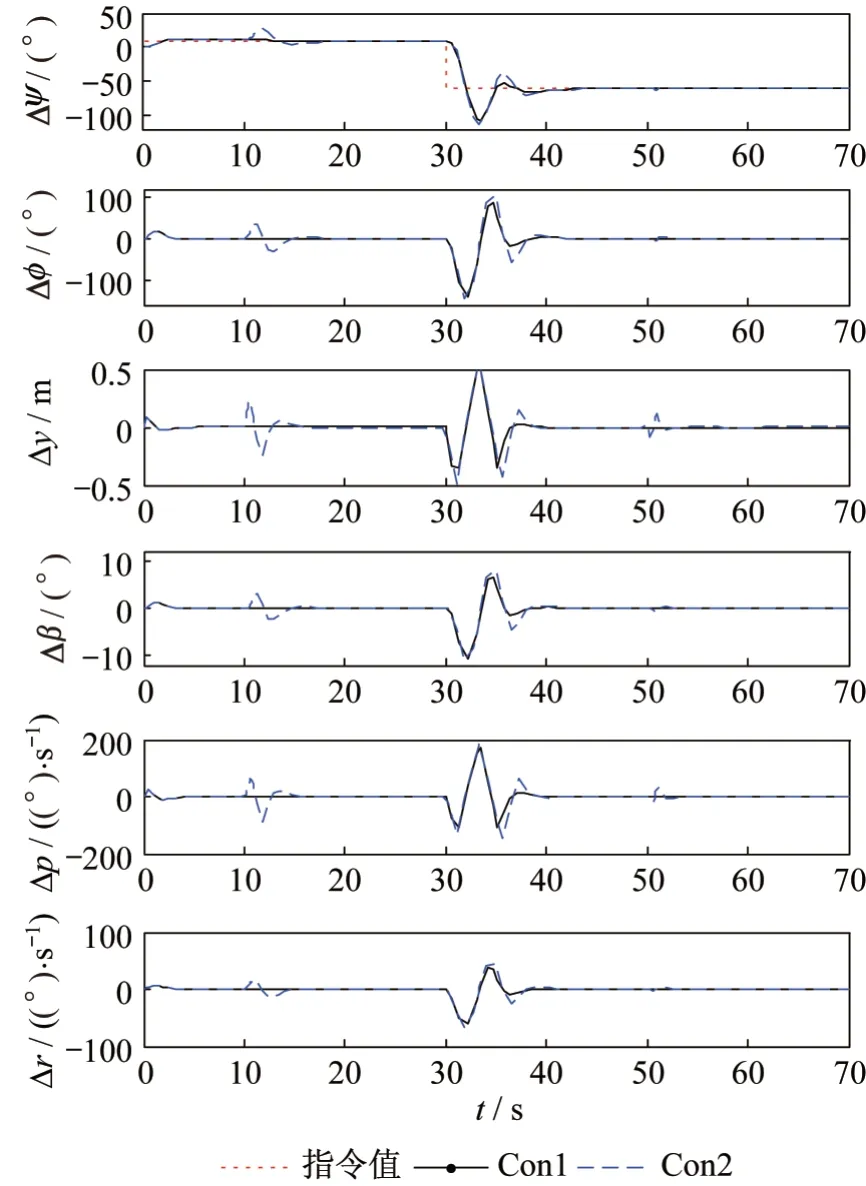
图7 偏航角控制器响应曲线Fig.7 Response curves of yaw angle controller

3.4 改变滑块最大滑动速度和行程时的系统特性

由于选用蓄电池作为质量滑块，因此滑块质量在太阳能无人机设计完成后是不可人为改变的，可改变的只有滑块最大滑动速度和行程。为方便表述，分别记为vmax和Lmax。下面分别研究改变vmax和Lmax时系统特性的变化。

图8 反映了当Lmax＝0.6 m 时改变滑块最大滑动速度vmax所造成的偏航角响应特性的变化。图9 反映了当vmax＝0.5 m/s 时，改变滑块最大滑动行程Lmax所引起的偏航角响应特性的变化。可以看出，当在一定范围内改变滑块的最大滑动速度和行程时，控制系统仍然能够实现对太阳能无人机的稳定控制，这体现了控制器系统的鲁棒性。

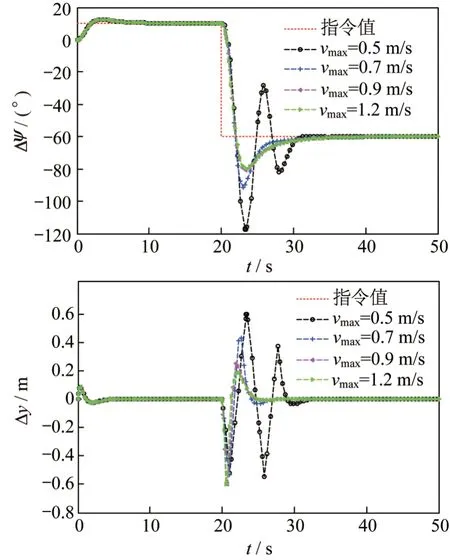
图8 滑块不同滑动速度下系统响应Fig.8 System response at different speeds of the slider

图9 滑块不同滑动行程下系统响应Fig.9 System response at different strokes of the slider

值得注意的是：①当Lmax增加或vmax减小时，系统超调量会有较大幅度增加，由于控制器的设计是基于小扰动线性化假设展开的，系统超调量过大有可能会导致系统状态超出线性近似范围，进而产生难以估计的后果，甚至造成系统发散；②控制系统动态响应过程对滑块vmax的变化较为敏感，当滑块移动速度过慢时，会造成系统时滞现象明显，导致系统发散；另一方面，当滑块滑动速度快到一定程度时，系统动态特性不再随着vmax的变化而产生明显改变。

基于上述分析，并结合图5的仿真结果可知，虽然滑块行程Lmax的增加会带来无人机操纵能力的提升，但也会导致系统超调量的增加，因此在实际应用中滑轨长度的选择应适中。此外，过低的滑动速度vmax可能会导致系统发散，过高的vmax对系统动态性能的提升又是有限的，因此驱动滑块的舵机作动速度的选择也应适中。

3.5 控制效率分析

为了衡量变质心控制方案的控制效率，需要一个合适的评价指标。对此，定义了适用于变质心方案的滑块效率系数ly和适用于传统气动舵面控制方案的副翼效率系数lδa，二者的物理意义类似，其中前者是指单位滑块偏移量所引起的滚转力矩系数的改变值，其表达式可写为

后者则代表副翼单位偏转时所引起的滚转力矩系数的变化量，通常为一个常值。

图10 给出了以上两个效率系数随无人机飞行速度的变化趋势。可以看出：在低速区域内ly远大于lδa；而在高速区域内，尽管lδa大于ly，但二者的差距并不明显。因此，对于飞行速度普遍较低的小型固定翼无人机来说，变质心控制方案相对于传统的气动舵面控制方案来说，具备更高的控制效率。

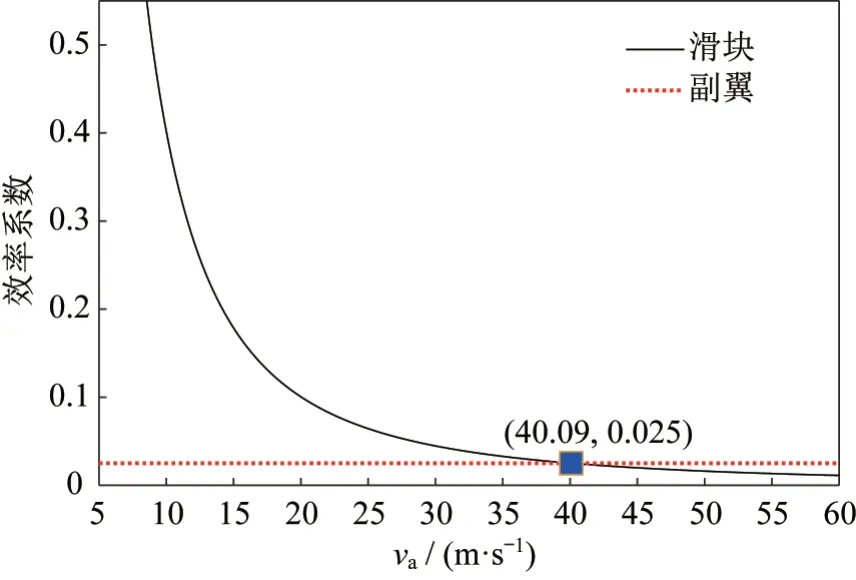
图10 效率系数随速度变化曲线Fig.10 Efficiency coefficients vs.airspeed

4 结束语

本文选取蓄电池作为变质心太阳能无人机的质量滑块，实现了对副翼的替代，可用于操纵无人机的横向运动，且具有良好的鲁棒性和抗风性。滑动行程的增加会带来操纵能力的提升，但这也会导致系统超调量的增加。滑动速度主要影响系统的动态响应特性，过低的滑动速度会导致系统时滞明显，甚至造成系统发散，当滑动速度达到一定量级后，系统动态性能不再有明显的提升。本文设计的横向控制系统以蓄电池代替方向舵作为控制机构，仅以滑块偏移量作为控制量，构造简单，便于工程实现。通过分析得出，滑轨长度和舵机作动速度都应适中选择，从而为临近空间防御领域的工程应用提供参考。