基于序列凸优化算法的飞行器轨迹规划
李 臻,许冰青,李庆波,鄢雄伟,李博雅
(1.上海机电工程研究所,上海 201109;2.陆军驻上海地区军事代表室,上海201109)
0 引 言
助推滑翔式飞行器在飞行时,长时间处于稠密大气层内,热力学环境复杂恶劣,为了保证弹载设备及机身结构正常,飞行器必须满足热流、动压、过载等多方面的约束[1-2]。在工程优化领域,针对这类非线性规划问题,一般基于直接法求解,如序列二次规划等方法。例如,黄鲁豫等[3]基于序列二次规划方法研究了飞行器复合控制技术;李征等[4]基于序列二次规划解决了伪谱法转换后的无人机集群规划问题;Cui等[5]利用高斯伪谱法求解了基于线性协方差的弹道优化方法,解决火星再入问题。然而,这类方法在使用中常存在初值敏感、收敛较慢的问题。
近年来,凸优化方法以其独特的理论优势逐渐受到青睐。对于一个凸问题而言,基本性质明确了其得到的局部最优解即为全局最优解,算法解集的最优性得到了保证[6]。然而,凸优化方法在一般非线性问题中的应用存在一定限制,要求原问题保持凸性,而一般的非线性问题具有高度的非凸性[7]。为此,需要将原非线性规划问题转化为一系列近似的线性规划子问题,通过迭代逐步逼近原问题的解,这一过程称为序列凸优化[8]。本文以助推滑翔式飞行器为应用背景,设计了在序列凸优化算法下的非线性规划方法,具有初值不敏感性、快速收敛性。
1 规划问题与模型
在半速度系下,建立无量纲的飞行器动力学模型,可表达为[9]

式中:r为单位地心距;θ、ϕ分别为经度和纬度;v为单位速度;γ、ψ分别为航迹角和航向角;α、σ分别为攻角与倾侧角;ω为地球自转速度;D、L为归一化后阻力和升力。
式(1)是关于6 个状态变量与2 个控制变量的强非线性方程,本文通过文献[10]所述方法,设计新的控制变量来对运动方程进行解耦处理,将原控制量攻角、倾侧角引入状态量中,扩维状态为
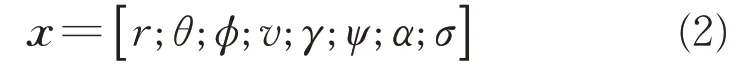
取攻角导数、倾侧角导数为新的控制变量u,新的扩维动力学方程可表达为
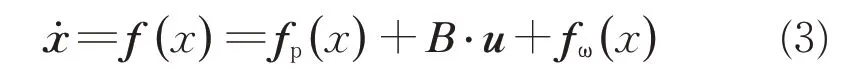
式中:动力学列向量fp(x)∈R8;控制量系数阵B∈R8×2;角速度相关列向量fω(x)∈R8。解耦后动力学模型中控制系数阵B为一常量,独立于状态参数。
飞行器规划问题中还存在一系列约束,如:①禁飞区约束,用Nf表示;②热流Q̇、动压q、过载n过程约束;③控制系统性能约束;④初末值约束等常见过程约束形式。可以记为

式中:rn、θn、ϕn为禁飞区的半径、中心点经纬度;ρ为大气密度;Q̇max、qmax、nmax分别为热流、动压、过载的约束极值;umax为控制的约束极值;xf为末状态。
基于上述分析,轨迹优化问题可以表述为:确定容许控制u(t)∈R2以及容许状态x(t)∈R8,使得由一个微分方程组(式(3))确定的系统,从给定的初始状态过渡到给定的终端状态,在满足规定约束(式(4))的同时,使性能指标函数J达到最小。轨迹优化问题P1的数学形式可表达为
Problem 1:
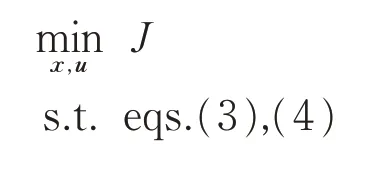
2 参数化方法
轨迹优化问题P1具有连续非线性非凸的形式,本文采用分段高斯伪谱法,将上述非凸问题离散。将原问题时域均分为N个区间,每段区间上选择N1个高斯点。原动力学方程在每段区间上可以离散为式(5)所示形式,其推导参见文献[11]。
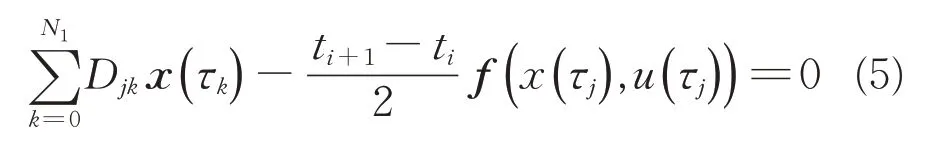
式中:τ为[-1,1]区间上的时间变量;ti为第i段区间的时间起点;由Djk构成的系数矩阵称为微分近似阵,j=1,…,N1,k=0,…,N1,可用D来表示 ,D∈RN1×(N1+1)。Djk的形式为
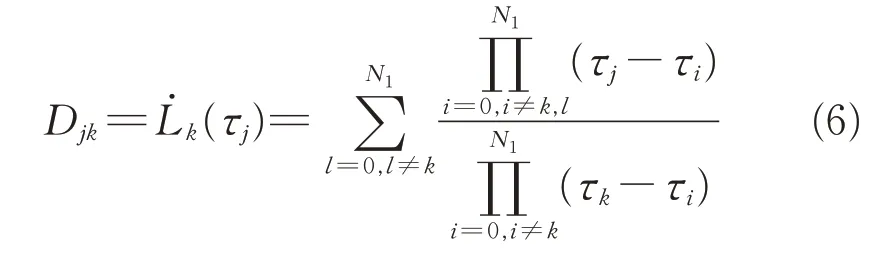
式(5)对应的是一个区间段上的微分等式约束,而该问题在全区间段[t0,tf]上共分为了N段,因此在整个规划问题中需要同时考虑这N个微分等式约束。为简化表达,以式(7)代表这一系列的等式约束。
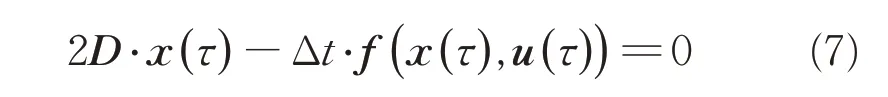
高斯伪谱法下系统微分方程只在高斯点处进行了离散近似,对于区间端点还需利用高斯求积公式约束,用x(τN1+1)、x(τ0)表示[ti,ti+1]区间端点状态
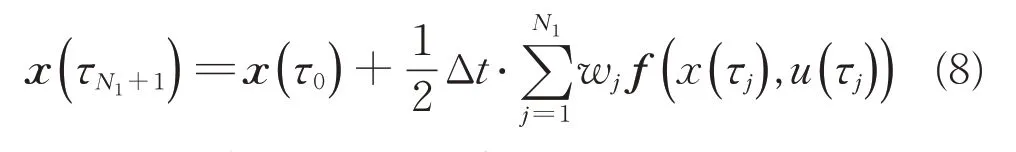
式中:wj为每一节点处的高斯权重,可表达为
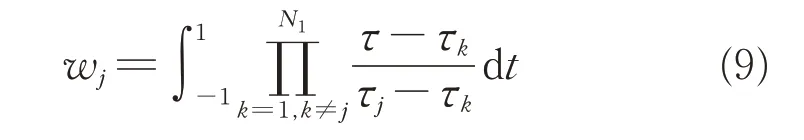
同样,在全区间上需考虑N次端点约束,采用相同方式,式(8)简记为
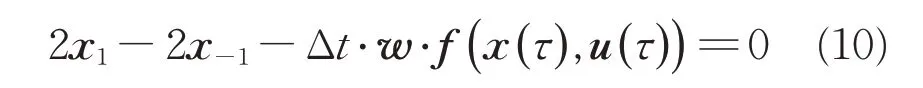
新的非线性规划问题P2形式为
Problem 2:

3 约束转化
对于扩维动力学方程(式(3)),以x*表示上一步子问题解,一阶线性展开后新的动力学方程可表达为

式中:A(x*)为动力学项fp(x)的偏导系数阵。
动力学方程中未展开地球自转项,原因在于该项在动力学方程中量级较小,近似处理不会产生较大误差。
采用相似的方式处理式(4)中的禁飞区约束、热流约束、动压约束、过载约束,形式为
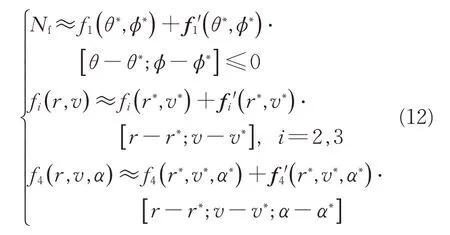
线性化只有在基准值附近才能保证近似精度,因此需要在原问题中附加一个置信域约束

式中:δx表示各归一化后状态量的极限偏差取值范围。
该问题中还存在以下约束:①对无动力滑翔飞行器而言,飞行过程伴随着能量耗散,因而速度曲线呈现出递减的趋势,满足Δv≤0;②飞行器作平衡滑翔飞行,满足δγ≤γ≤0;③飞行器高度会一直下降,满足Δr≤0。
至此,已完成了对问题P2中所有非线性约束的转化,非线性规划问题已经转化为有限维的线性规划问题P3。

4 带罚函数的序列凸优化算法
在一般性初值下,直接迭代求解问题P3是不可行的[12]。为了使算法具有初值不敏感性,并能以较快速度收敛到可行解。本文给出一种带罚函数的序列凸优化算法。设计如下:
1)第一步,在原问题P3 中对所有转化后的非线性约束项引入松弛变量ξ与ζ,并放弃置信域约束,该部分目标函数设置为式(14)所述形式,式中c1、c2、p为各项的常系数。
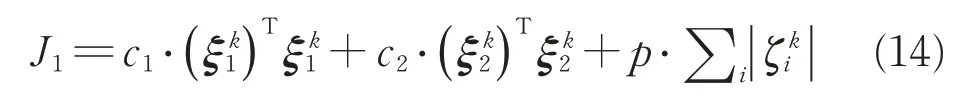
以第(k-1)次迭代值为基准,第k次迭代求解子问题SP1。子问题中用(·)k-1的形式代替前文(·)*,作为展开基值。(·)k元素为第k次迭代时待规划量。
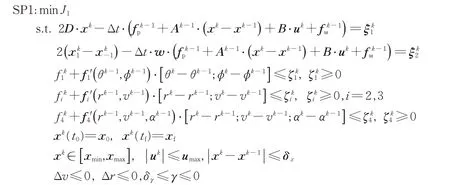
式中:ξk1、ξk2为微分等式约束对应的松弛变量;ζ ki为不等式约束下的松弛变量。所有松弛变量趋于0 时,第一步规划子问题SP1 与问题P3 在约束上是相同的。该步目的在于,在一个较差的初值下能寻找到合适可行域以初步满足约束条件。
由于子问题SP1 中不等式约束比微分约束更容易满足,令e0=不等式约束判断条件为:若e0<10-5,认为当前解在不等式约束上已经足够完备,转入下一步规划。
2)第二步,舍弃不等式约束相应的松弛因子,求解新的过渡子问题SP2,该部分目标函数设置为
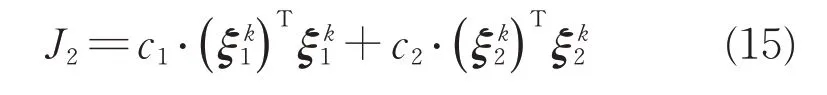

该步规划采用严格不等式约束,保留松弛微分约束,加速寻找初值过程。
从第二步规划过渡到第三步规划时,需考虑微分误差的求解情况。令,微分约束判别条件为:当eˉ≤10-8时,认为当前解对应的子问题SP2与问题P3在约束意义上足够接近,过渡到下一步。
3)第三步,回归问题P3,子问题SP3 目标函数重设为最小化置信域误差

式中:q为置信域系数;Δxkp由k次迭代时原控制变量Δαk与Δσk构成。
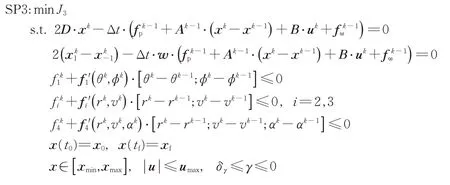
求解子问题SP3 时,若某一次计算结果使|Δxk|≤ε成立,则认为当前规划结果是满足原非线性规划问题P1的一组可行解。
带罚函数的序列凸优化算法流程如图1所示。

图1 带罚函数的序列凸优化算法流程Fig.1 The flow of sequential convex optimization with penalty function
5 仿真实验
对于求解单个凸优化问题的过程,本文采用的是SDTP3工具包。在应用时,要求输入的所有等式约束是仿射的,所有的不等式约束是凸的,即只解决数学意义上满足凸性的问题。因此,在配合本文所设计算法的情况下,可以应用于非线性规划问题求解。
该部分设计了一个仿真算例来验证上述序列凸优化算法的可行性。某型飞行器启滑段状态参数固定,根据飞行任务,要求在1 500s 后抵达西南方向1 500 km外的固定目标点,飞行中途存在一个禁飞区。控制约束与路径约束见表1。
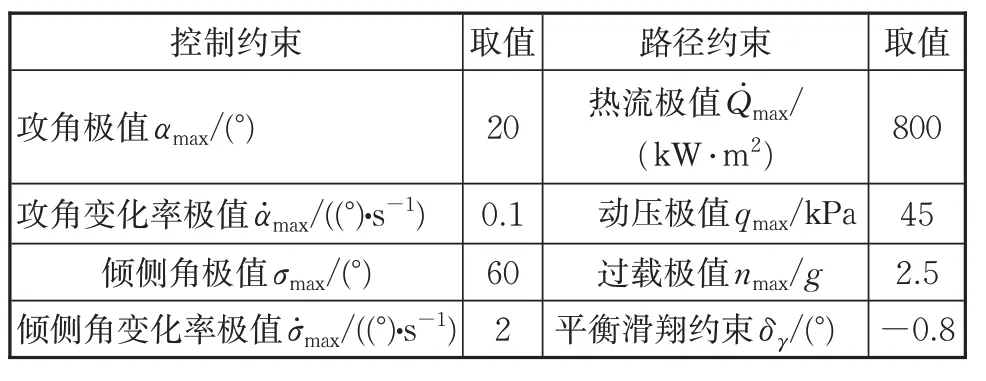
表1 控制约束与路径约束Tab.1 Control constraint and path constraint
算法中置信域约束与收敛条件取值为

松弛因子与置信域误差的常系数分别取c1=100、c2=200、p=10、q=0.2。
为了更好展现本节算法的性能,将其与非线性规划领域已广泛应用的求解工具包GPOPS-2 进行对比。在数值仿真阶段,GPOPS 软件与序列凸优化方法输入的原问题相同,为P1的形式。并且求解动力学模型均采用式(3)所述的扩维模型。伪谱法参数如表2所示。

表2 伪谱法参数Tab.2 The parameters in the pseudo-spectral method
仿真结果如图2~11 所示。为体现算法的初值不敏感性,迭代的初值弹道直接按常值攻角、常值倾侧角的控制规律提供,不满足绝大部分约束条件。
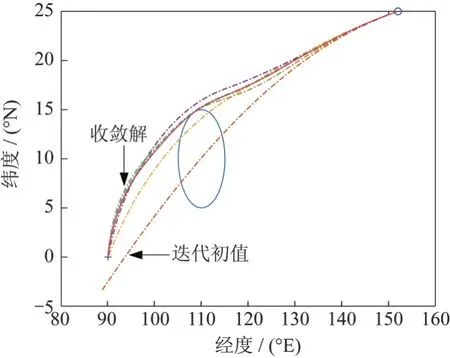
图2 迭代中水平面轨迹变化Fig.2 The trajectories during iteration
在该初值下,序列凸优化算法经过7 次迭代运算解收敛,耗时142.2 s。迭代中每次运算的轨迹变化如图2所示,其中红色加粗实线段代表最后收敛的轨迹,初值轨迹则是图中最下方穿过禁飞区的那一条曲线。可以明显看出,求解过程中,解对应的轨迹不断向禁飞区左侧挪动,最后收敛。运算中目标函数变化如图3 所示,随迭代进行趋于0,因此最后得到的解是可信的。
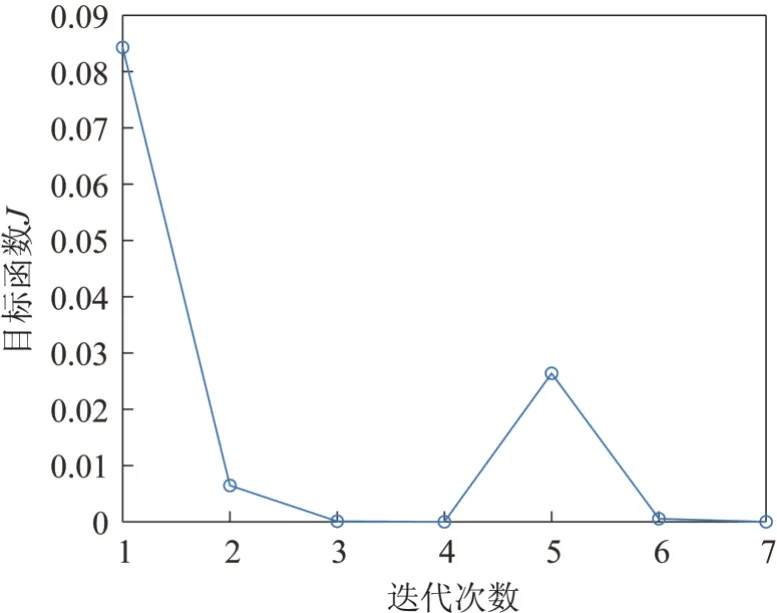
图3 迭代中目标函数值变化Fig.3 Objective function values during iteration

图4 两种规划水平面轨迹Fig.4 The horizontal trajectory using two methods

图5 两种规划空间轨迹Fig.5 The space trajectory using two methods

图6 两种规划攻角规律Fig.6 The profile of attack angle using two methods
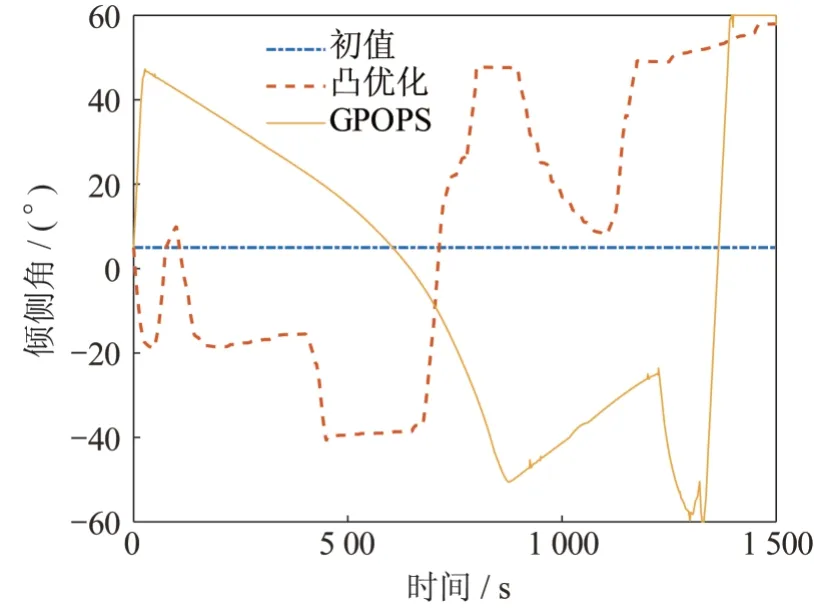
图7 两种规划倾侧角规律Fig.7 The profile of bank angle using two methods
两种优化方法下的可行解结果对比见图4~11,其中红色虚线代表凸优化仿真结果,蓝色点划线代表凸优化初值,黄色实线代表GPOPS 方法仿真结果。
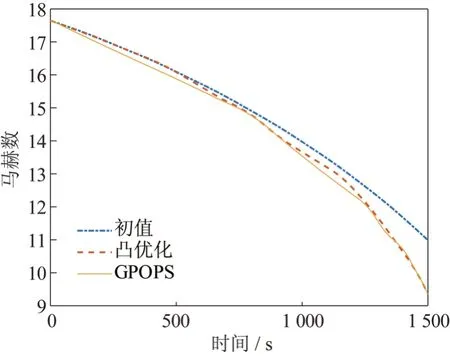
图8 两种规划速度变化Fig.8 The profile of velocity using two methods
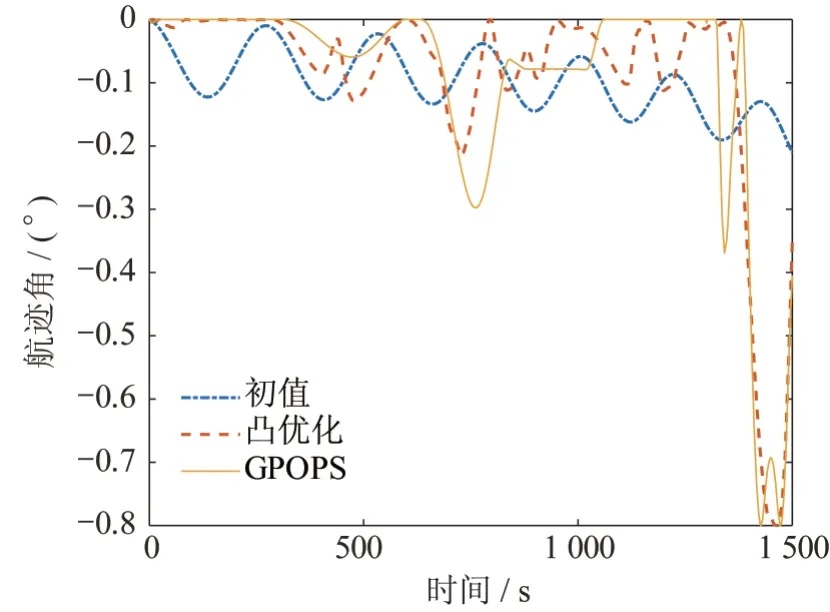
图9 两种规划航迹角变化Fig.9 The profile of flight path angel using two methods

图10 两种规划热流密度变化Fig.10 The density of heat flow using two methods
由于未额外约束可行解过程参数,因此从结果上看二者有差异,但均满足了所有约束要求。凸优化方法找到的可行解是从禁飞区左侧绕飞后抵达目标,而GPOPS 方法的解是从禁飞区右侧绕飞后抵达目标,因此控制量规律也会产生相应变化。
总体而言,序列凸优化方法与GPOPS 软件均找到了合适可行解,结果对比如表3 所示。在相同仿真环境下,GPOPS方法经过了6次迭代,耗时465.5 s,慢于本文设计的序列凸优化算法的速度;求解精度为10-3,也不及本文设计的算法。
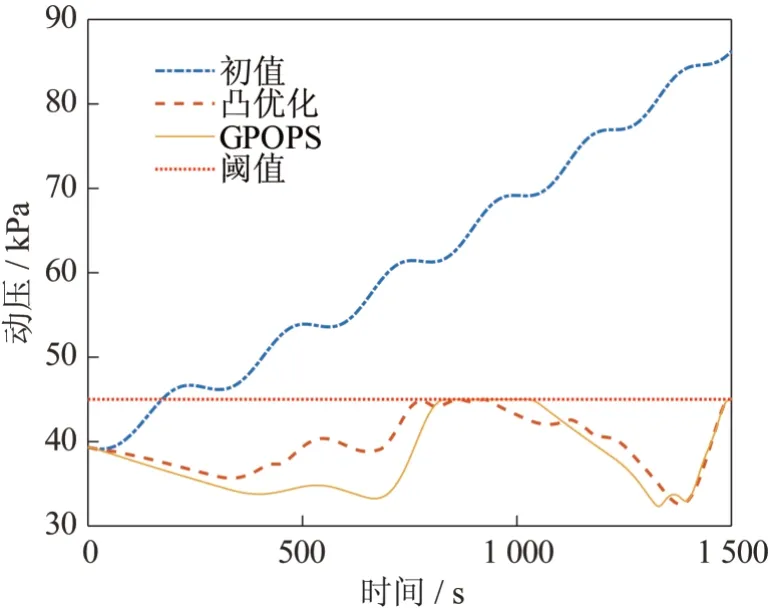
图11 两种规划动压变化Fig.11 The dynamic pressure using two methods
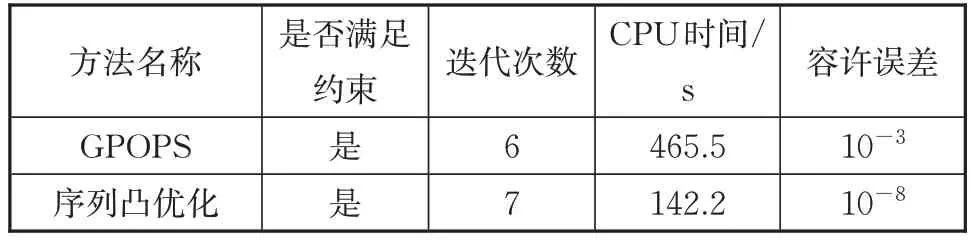
表3 方法结果对比Tab.3 Comparison of Results
6 结束语
本文以助推滑翔式飞行器在多约束条件下轨迹规划为应用背景,设计了针对一般非线性规划问题寻找可行解的序列凸优化算法。通过算例仿真,验证了设计算法可行性,能克服初值敏感并以较快速度收敛,满足多约束要求。

