单位球上含梯度项的椭圆边值问题的正径向解
唐 颖, 李永祥
(西北师范大学数学与统计学院, 兰州 730070)
非线性项中含有梯度项的一般椭圆边值问题出现在应用数学与物理的许多领域, 其可解性的研究有重要价值. 本文考虑如下单位球上含梯度项的椭圆边值问题(BVP)
(1)
正径向解的存在性, 其中Ω={x∈RN: |x|<1},N≥2,I=[0,1],R+=[0,+∞),f:I×R+×R+→R+为非线性连续函数.
对于非线性项中不含梯度项的特殊情形, 即简单椭圆边值问题
其径向解的存在性已有较深入的研究, 见文献[1-5]. 对于非线性项含梯度项的情形, 当Ω为环形区域或球外部区域时, 部分文献[6-8]讨论了其正径向解的存在性.其中,文献[6-7]在非线性函数f(r,ξ,η)非负且允许f关于ξ,η超线性或次线性增长的条件下利用不动点指数理论获得了BVP(1)正径向解的存在性. 对于f关于ξ,η超线性增长的情形, 文献[6-7]还假设f满足Nagumo型增长条件, 该条件限制了f关于η至多二次增长. 然而, 对球域而言此结果不成立. 事实上, 文献[6]给出了一个例子:
(2)

(3)
没有正径向解. 此时 BVP(3)为BVP(2)中a=1,b=0的特例,从而BVP(2)在球域上无正径向解. 这说明文献[6]中的结论对球域上的BVP(1)不成立.
一般来说, 研究球域上的椭圆边值问题径向解的存在性比环域及球外部区域上的情形更复杂. 目前关于球域上BVP(1)径向解的存在性结果还很少. 最近, 文献[9]应用上下解方法研究了单位球上BVP(1)正径向解的存在性,在非线性项f满足适当的不等式条件下获得了BVP(1)正径向解的存在性, 该不等式条件允许f(r,ξ,η)关于ξ与η负向超线性增长,在f(r,ξ,η)关于η超线性增长情形下要求f(r,ξ,η)关于η满足 Nagumo 型增长条件.
本文继续研究单位球上BVP(1)正径向解的存在性. 在与文献[9]不同的不等式条件下, 我们给出BVP(1)正径向解的存在性结果,其中的不等式条件允许f(r,ξ,η)关于η可超线性增长.
2 预备知识
对问题(1)的径向对称解u=u(|x|), 我们令r=|x|, 将其转化为区间I上的常微分边值问题(BVP)
(4)

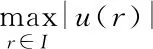
构成的 Banach 空间.
为了讨论BVP(4), 我们先考虑相应的二阶线性边值问题(LBVP)
(5)

引理2.2对∀h∈C+(I), LBVP(5)的解u=Sh满足下列条件
(ii)u≥0,u′≤0.
证明 (i) 由Hölder不等式有
(ii) ∀h∈C+(I), 方程(5)两边同乘rN-1得
-(rN-1u′(r))′=rN-1h(r),r∈I
(6)
对方程(6)两边积分, 应用(5)中的边界条件得
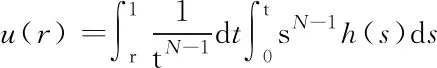
因此,
u(r)≥0,u′(r)≤0,r∈I.
证毕.
记P={u∈C1(I)|u(r)≥0,r∈I},则P为C1(I)中的闭凸锥. 由引理2.1及引理2.2,ii), LBVP(5)的解算子S:C+(I)→P为全连续算子.
3 主要结果
定理3.1设f:I×R+×R+→R+连续. 若f满足
(H1) 存在常数a,b≥0, 满足a/2+b<1及C0>0, 使得
f(r,ξ,η)ξ≤aξ2+bη2+C0,
(r,ξ,η)∈I×R+×R+;
(H2) ∀M>0, 存在单调递增的连续函数gM:R+→(0,+∞), 满足
(7)
使得
f(r,ξ,η)≤gM(η), (r,ξ,η)∈I×[0,M]×R+
(8)
则BVP(1)至少有一个正径向解.
证明 ∀u∈P,令

则F:P→C+(I)连续且把有界集映为有界集. 定义映射A=S∘F.由S:C+(I)→P为线性全连续算子知算子A:P→P为线性全连续算子. 再由S的定义, BVP(4)的正解等价于算子A的正不动点.
考虑同伦簇方程
u=λAu, 0<λ<1
(9)
下面我们证明方程簇(9)的解集在P中有界. 设u∈C2(I)∩C+(I)为方程簇(9)中某个λ∈(0,1)对应的方程的解, 则u=S(λF(u)). 令h=λF(u),按S的定义,u为h=λF(u)相应的LBVP(5)的解. 因此,u∈C2(I)∩C+(I)满足方程
(10)
方程(10)两边同乘u(r), 由条件(H1)及引理2.2(ii)有
-u″(r)u(r)≤
λf(r,u(r),|u′(r)|)u(r)≤
f(r,u(r),|u′(r)|)u(r)≤
au2(r)+b|u′(r)|2+C0,r∈I
(11)
式(11)两端同时在I上积分, 由引理2.2(i)可得

从而
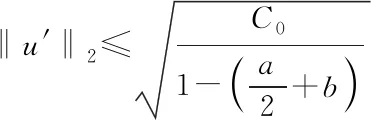
因
故有估计
(12)
对此M>0, 由Nagumo型增长条件(H2)可知, 存在连续函数gM:R+→(0,+∞)满足式(7), 使得f满足式(8). 由式(7)可知, 存在常数M1=M1(M)>0, 使得
(13)

则0≤r1
λf(r,u(r),|u′(r)|)≤
f(r,u(r),|u′(r)|)≤
gM(-u′(r)).
所以
上式两边从r1到s1积分得
u(r1)-u(s1)≤u(r1)≤‖u‖C≤M
(14)
对式(14)左端做变量代换ρ=-u′(r), 有
(15)

即方程簇的解集在C1(I)中有界. 由锥上的Leray-Schauder不动点定理[10]知A在P中有不动点, 该不动点为BVP(4)的正解,从而BVP(1)有正径向解.证毕.
在定理3.1中,f(r,ξ,η)关于η可超线性增长, 见例3.3. 特别地, 当f(r,ξ,η)关于ξ,η均一次增长时, 我们有下述推论.
推论3.2设f:I×R+×R+→R+连续. 若f满足
(H3) 存在常数a,b≥0, 满足a/2+b<1及C0>0, 使得
f(r,ξ,η)≤aξ+bη+C0,
(r,ξ,η)∈I×R+×R+,
则BVP(1)至少有一个正径向解.
证明 (H3)⟹(H2)显然,下证(H3)⟹(H1). 任取(r,ξ,η)∈I×R+×R+,令
利用不等式2pq≤p2+q2,p,q∈R并由条件(H3)有
f(r,ξ,η)ξ≤aξ2+bξη+C0ξ=
aξ2+2p1q1+2p2q2≤
aξ2+p12+p22+q12+q22
(16)
令
由常数a,b≥0,满足a/2+b<1知
所以a1/2+b1<1.由式(16)有
f(r,ξ,η)ξ≤a1ξ2+b1η2+C,
(r,ξ,η)∈I×R+×R+.
因此条件(H1)成立. 由定理3.1, BVP(1)有正径向解.
例3.3设N≥2.考虑单位球Ω={x∈RN: |x|<1}上含梯度项的椭圆边值问题
对应于BVP(1), 相应的非线性项为
(r,ξ,η)∈I×R+×R+
(18)
当‖u‖C≤M时,
C1(M)+C2η2.
令gM(η)=C1(M)+C2η2,则f(r,ξ,η)满足条件(H2).
下面验证f(r,ξ,η)满足条件(H1).取
则
由式(18)有
0≤f(r,ξ,η)ξ=
aξ2+bη2+C0,(r,ξ,η)∈I×R+×R+,
即f(r,ξ,η)满足条件(H1). 从而由定理3.1知BVP(17)有正径向解.

