基于相变材料GST的红外隐身多层膜设计与光谱性能研究

黎思睿, 李 佳, 刘 科, 2, 黄奕嘉, 李 玲, 周晓林

(1. 四川师范大学物理与电子工程学院, 成都610101；2.西南交通大学材料科学与工程学院, 成都611756)

1 引 言

传统的红外隐身材料多是在红外大气窗口具有低发射率的材料[1-6]. 此类伪装材料的发射率固定且不可控. 当背景温度发生变化时, 背景的辐射温度和材料的辐射温度往往不匹配, 因而失去伪装能力[7]. 所以传统的低发射率材料难以适应背景温度变化情况下红外隐身的需求. 为了实现在不同背景温度条件下的红外隐身, 我们需要研究具有可调发射率的红外隐身材料. 根据基尔霍夫定律, 物体的发射率等于热平衡状态下的吸收率[8]. 所以要实现发射率可调, 就要实现吸收率可调. 此前, 已有研究者利用外加偏压来改变石墨烯的电导率, 进而改变共振频率, 实现电压调频吸收的可调谐吸收器[9]. 众所周知, 石墨烯是一种由单层碳原子构成的二维材料, 具有不同费米能级的石墨烯的表面电导率不同[10]. 所以, 利用静电掺杂等技术在一定范围内调节石墨烯的费米能级, 即可实现可调谐超材料吸收器[10-13].

基于石墨烯的可调谐超材料吸收器需要持续地消耗能量来维持它的某一状态. 相变材料是一种能在激光、温度和外加电场等外部条件的刺激下实现从一个状态到另一个状态转换的特殊材料[14-18]. Ge2Sb2Te5(GST)是一种常用于超材料设计的相变材料，且数据存储领域GST已经被应用了多年[14]. GST是一种可以在晶态和非晶态之间转换的材料[19]. 为了表述简单, 我们将GST为非晶态时的结构称为a-GST结构, 将GST为晶态时的结构称为c-GST结构, 而将中间态GST构成的结构简称为 i-GST结构. 在红外波段, 不同状态的GST拥有不同的电磁性质, 晶态的GST (c-GST)在红外大气窗口为损耗材料, 而非晶态的GST(a-GST)在此波段为电磁透明材料[7, 20]. 更重要地是, 除非再次满足相变条件, 否则在室温下某一状态的GST将维持多年, 即不需要额外的能量去维持GST的状态稳定[20]. 本文正是利用该材料的特殊性质, 提出了一种基于GST的具有可调吸收率的红外吸收器, 使之具有热红外隐身的潜在应用价值.

随着科技的进步, 单一波段的隐身技术很难适应不断发展的多波段探测技术, 因此多波段兼容隐身技术愈发显得重要[21]. 已经有许多研究者开展了关于红外-可见、红外-雷达和红外-激光兼容隐身的研究[1, 4, 6, 22]. 为了让设计的结构能进一步实现可见光隐身, 我们利用结构生色原理获得不同的表面颜色. 结构色主要是利用光和微纳结构之间的相互作用产生颜色, 是基于干涉、衍射和散射的基本光学现象[23]. 本文利用薄膜干涉原理, 通过改变结构的薄膜厚度来改变结构的表面颜色, 同时维持结构的红外吸收性能.

我们设计了一种利用单一多层膜结构实现吸收率可调谐, 且具备可调结构色功能的超材料吸收器. 该吸收器可同时实现在红外及可见光两个波段对电磁波的独立调控功能, 使其具有与背景颜色融合的表面颜色且兼具红外隐身能力. 在背景热辐射和颜色不同的情况下，它可以伪装自己, 实现红外-可见光兼容隐身.

2 设计原理与结构

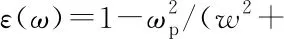
本文利用传输矩阵法计算整个结构的红外吸收光谱. 传输矩阵法是一种常用于计算多层膜结构的计算方法. 它具有速度快、矩阵元素少、易于编码的特点[27-28]. 这些特点使之很容易便能和各种优化算法结合, 用于不同功能的多层膜结构的优化设计[29]. 具体的设计和计算方法见我们之前的工作[30]. 底层Au的厚度固定为足以抑制透射的150 nm, 所以结构的透射近似等于0. 因此, 吸收性能可利用A=1-R来计算, 其中A代表吸收率,R代表透射率. 在使用遗传算法优化设计过程中, 我们使用适应度函数objfun=R(λ), 其中λ=10.5 μm, 而R是利用传输矩阵法计算的波长为λ时结构的反射率. 优化变量为薄膜厚度, 即H1、H2和H3. 利用遗传算法我们可以得到适应度函数最小时对应的薄膜厚度. 由于遗传算法的随机性, 经过多次优化后, 最佳的厚度为H1=180 nm,H2=100 nm和H3=345 nm.

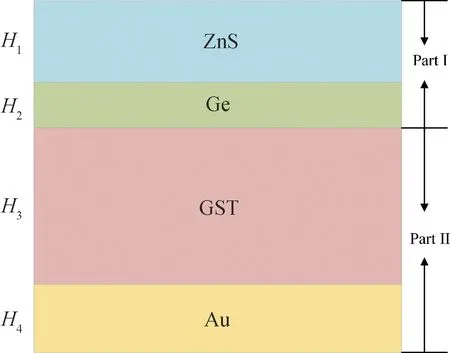
图1 吸波器的示意图, 每层的厚度从顶部到底部分别记为H1,H2,H3和H4

表面颜色的调控是利用薄膜干涉条件实现的. 薄膜干涉生色是非常常见且简单的结构色的来源[31]. 一般来说, 发生相消干涉的波长对应着反射谷的波长, 同理相长干涉对应着反射峰[32].

我们以最典型的单层薄膜干涉为例. 由于光从光疏介质射向光密介质时, 反射光会有半波损失, 所以薄膜是否附着在折射率较高的衬底上会影响薄膜干涉条件[23]. 对于附着在具有较高折射率的衬底上的薄膜, 干涉条件为：

2nfdcosθb=(m-1/2)λ1

(1)

2nfdcosθb=mλ1

(2)

其中,λ1为发生相消干涉的波长；λ2为发生相消干涉的波长；m为整数；θb为入射角；d和nf分别代表薄膜的厚度和折射率. 从干涉条件可知, 我们可以通过改变薄膜的厚度来改变发生干涉的波长. 同时, 薄膜的反射光谱也会发生变化, 由此可以得到不同颜色的薄膜.

在正入射时, c-GST结构的红外吸收情况如图2(a)中的红实线所示. 吸收器在10.5 μm处有94.93%的最大吸收率. 且结构在8～13 μm的平均吸收率为65.59%. 而a-GST结构的红外吸收情况如图2(a)中的黑虚线所示, a-GST结构在8～13 μm的最大吸收率仅为9.19%, 且在该波段平均吸收率低达4.9%. 这说明此吸收器可在单一结构中通过改变GST的状态实现最大吸收率从94.93%到9.19%的调控.

通过控制退火时间或温度等外部条件使GST部分结晶, 可以得到中间态GST(i-GST)[7, 20]. 为了进一步说明所提出结构的吸收率的连续可调性, 我们还设计并模拟计算了不同的中间态GST构成的i-GST结构. i-GST的介电常数可由Lorentz-Lorenz关系获得[7, 33]：

(3)

其中m代表GST的结晶率, 取值范围为0～1；εc和εa分别代表晶态GST和非晶态GST的介电常数；εi代表中间态GST的介电常数. 由图2(b)可得, 当中间态GST的结晶率逐渐上升时, 结构的吸收性能也有提升, 当结晶率为0.25、 0.5和0.75时, 结构的最大吸收率分别为23.15%、43.80%和70.51%, 而结构在8～13 μm的平均吸收分别为12.33%、25.37%和45.34%. 也就是说, 可以通过控制GST的相变来连续控制结构的吸收率. 具有这样特点的吸收器可以应用于具有不同背景温度的热红外隐身.

物体的表面颜色与其在可见光波段的反射光谱有关, 而结构色的产生主要与顶部的两层薄膜反射有关. 计算过程中使用的ZnS和Ge的光学常数来自参考文献[34-35]. 如图2(c)所示, 该结构的反射光谱在462 nm处存在反射率约50.72%的反射峰, 也就是说, 在8～13 μm波段具有可调吸收率的同时, 还兼具特定的颜色.

此外, 因结构色的产生主要与顶部的两层薄膜有关. 如图1所示, 我们将顶部两层定义为Part I, 剩下的底部两层定义为Part II. 如图2(c)所示, 首先, 我们分别模拟计算了只含Part I结构的可见光反射光谱(红虚线), 以及包含Part I和Part II两部分整体结构的反射光谱(黑实线). 研究表明, 在波长小于600 nm时, 两种结构的可见光反射光谱的差别并不大, 两条曲线基本重合. 其次, 如图2(d)所示, 仅存在Part I结构的可见光透射光谱(蓝虚线)中, 当波长小于600 nm时, 透射率非常小；而当波长大于600 nm时, 透射率开始增大, 但不高于10%. 这一现象与Ge在可见光波段的光学性质有关. Ge在可见光波段有着相对较高的消光系数, 是损耗材料[35]. 因此Part I中厚度为100 nm的Ge薄膜吸收耗损了大部分ZnS薄膜透射的光, 即入射的可见光大部分无法穿透Part I中的Ge薄膜. 由此, 结构色主要由顶层Part I 产生, 且实现了对可见光的独立调控. 为了进一步说明顶层薄膜厚度对结构色颜色的调控功能, 顶层ZnS的厚度分别设计为150、180、210和240 nm, 反射光谱如图3(a)所示, 由图3(a)可知, 不同顶层厚度结构的可见光反射光谱对应的反射峰波长明显不同. 如图3(b)和3(c)所示, 计算了顶层厚度H1在130和260 nm之间变化时, 结构的CIE坐标值及其对应颜色, 并将其在CIE 1931色度图中用黑点标出. 由图3可知, 我们可以通过改变顶层ZnS的厚度改变结构的表面颜色, 进而使结构与环境融合, 实现伪装. 同时考虑到结构的红外吸收性能, 此结构可以分别通过控制顶层厚度和GST的相变过程, 调控相应波段的光谱, 实现可见和红外的兼容隐身.

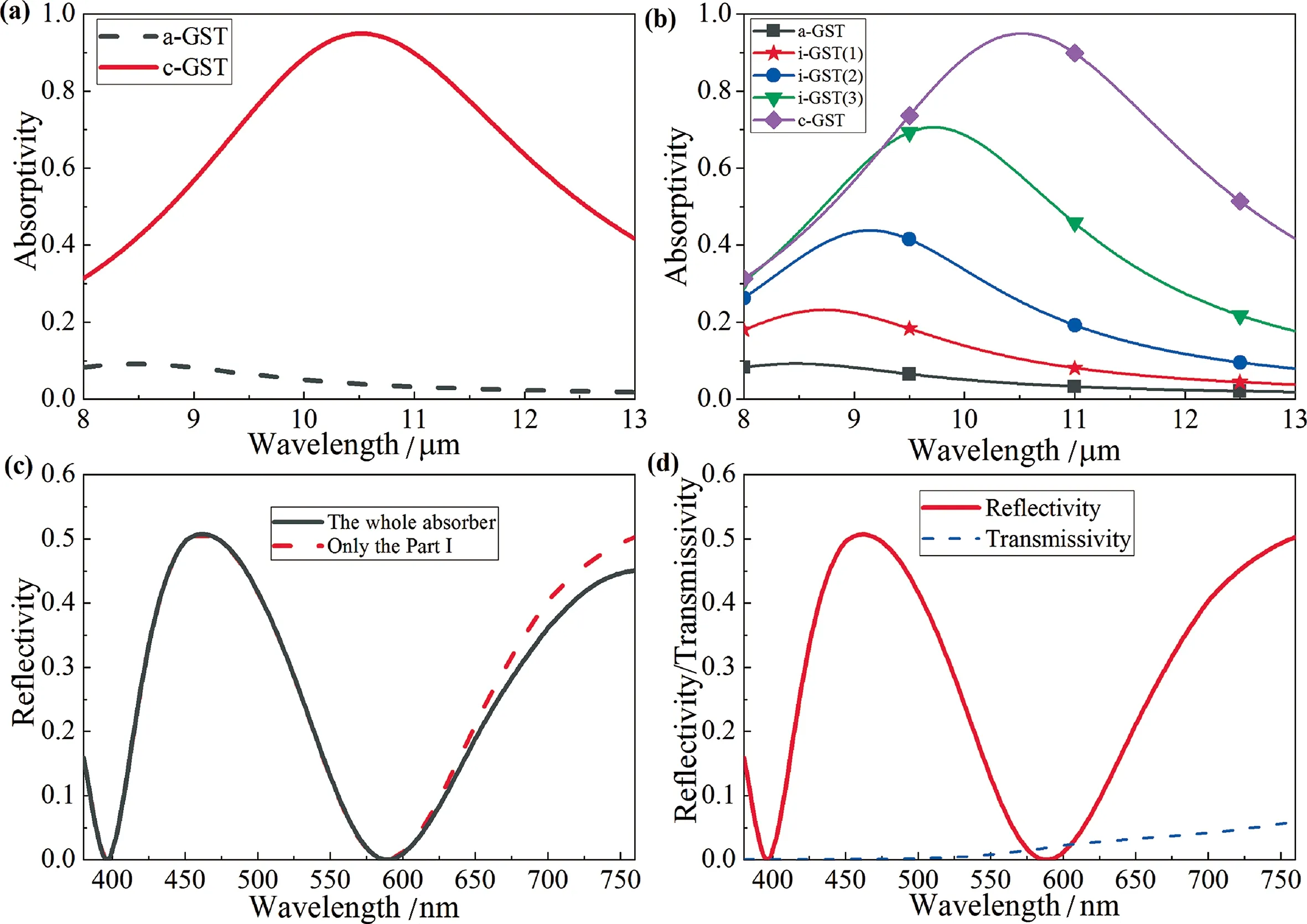
图2 (a) a-GST结构(虚线)及c-GST结构(实线)的吸收光谱; (b) GST的结晶率不同时结构的红外吸收光谱, 其中i-GST的结晶率分别为0.75(i-GST(3))、0.5(i-GST(2))和0.25(i-GST(1))；(c) 整个结构(实线)和仅存在Part I(虚线)的情况的可见光反射光谱; (d) 仅存在Part I结构的可见光反射(实线)和透射(虚线)光谱

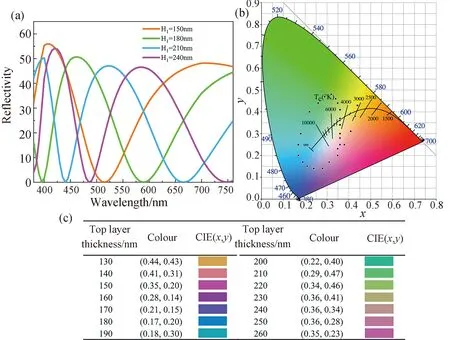
图3 顶层厚度对可见光反射光谱和表面颜色的影响: (a)模拟计算的吸波器在顶层厚度H1不同的情况下的可见光反射光谱; (b)在CIE1931色度图中用黑点标记的H1以5 nm为步长从130 nm变化到260 nm的CIE(x,y)色度坐标; (c)结构的顶层厚度从130 nm变化到260 nm 的颜色及其对应色度图坐标CIE(x, y)(线上彩色)

本文结构的红外吸收主要归功于GST本身的损耗特性以及干涉效应. 如前文所述, 在红外波段c-GST是损耗材料, 而a-GST是无损材料，这与不同状态GST结构的吸收率是对应的. 为了进一步说明结构和材料对吸收性能的影响, 我们计算了不同波长时不同状态的GST结构的功率损耗密度分布. 如图4(a)所示, c-GST结构中, 吸收大多发生在具有固有损耗的c-GST层中, 同时底部的Au层中只发生较少部分的吸收. 而如图4(b)所示, 在a-GST结构中, a-GST层中并不存在吸收损耗, 只有底层Au中存在吸收, 这对应着a-GST结构小于10%的吸收. 这说明了c-GST的固有损耗对结构实现红外吸收的贡献.

为了实现a-GST结构的低吸收, 底层金属我们选择了低固有损耗的贵金属Au. 作为对比, 我们模拟计算了底层金属材料为高损耗的镍铬合金的结构的吸收率(结构参数分别为H1=180 nm,H2=100 nm,H3=270 nm和H4=150 nm). 如图4(c)所示, 当GST为晶态时, 底层材料Au和镍铬合金的结构都有大于90%的最大吸收率. 而且底部金属为镍铬合金的c-GST结构的吸收带宽更宽, 这是因为镍铬合金本身具有高固有损耗. 如图4(d)所示, 当结构中的GST为非晶态, 底部材料为镍铬合金的结构的最大吸收率仍高达94.52%, 而平均吸收高达69.41%. 即底部材料为镍铬合金的结构不能通过调节GST的状态调节结构的红外吸收率. 因此, 镍铬合金之类的高损耗金属材料不适合作为吸收率可调的超材料吸收器的底层金属.

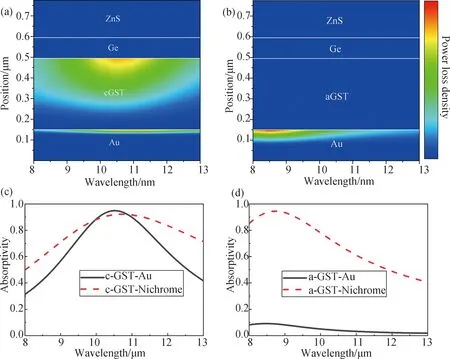
图4 功率损耗密度随波长和位置变化的分布和不同底部材料的结构的吸收光谱: 在8～13 μm范围内, (a) c-GST结构及 (b) a-GST结构功率损耗密度随波长和位置变化的分布; 底层材料分别为Au和镍铬合金时, (c) c-GST结构和(d) a-GST结构的吸收光谱(线上彩色)

由前面的分析可知, 设计的结构可以通过改变顶层薄膜厚度改变结构的表面颜色, 实现对可见光的独立调控. 因此有必要探究顶层薄膜厚度的变化是否对结构的红外吸收性能有较大影响. 图5(a)计算了顶层ZnS厚度在130～260 nm范围内变化时, 结构在8～13 μm的吸收光谱. 可以看出, 当顶层厚度变化时, 结构仍保持着出色的吸收表现, 其最大吸收率始终大于94%. 这意味着顶层厚度的变化对吸波器的吸收性能影响较小, 不会造成结构的吸收性能明显下降.

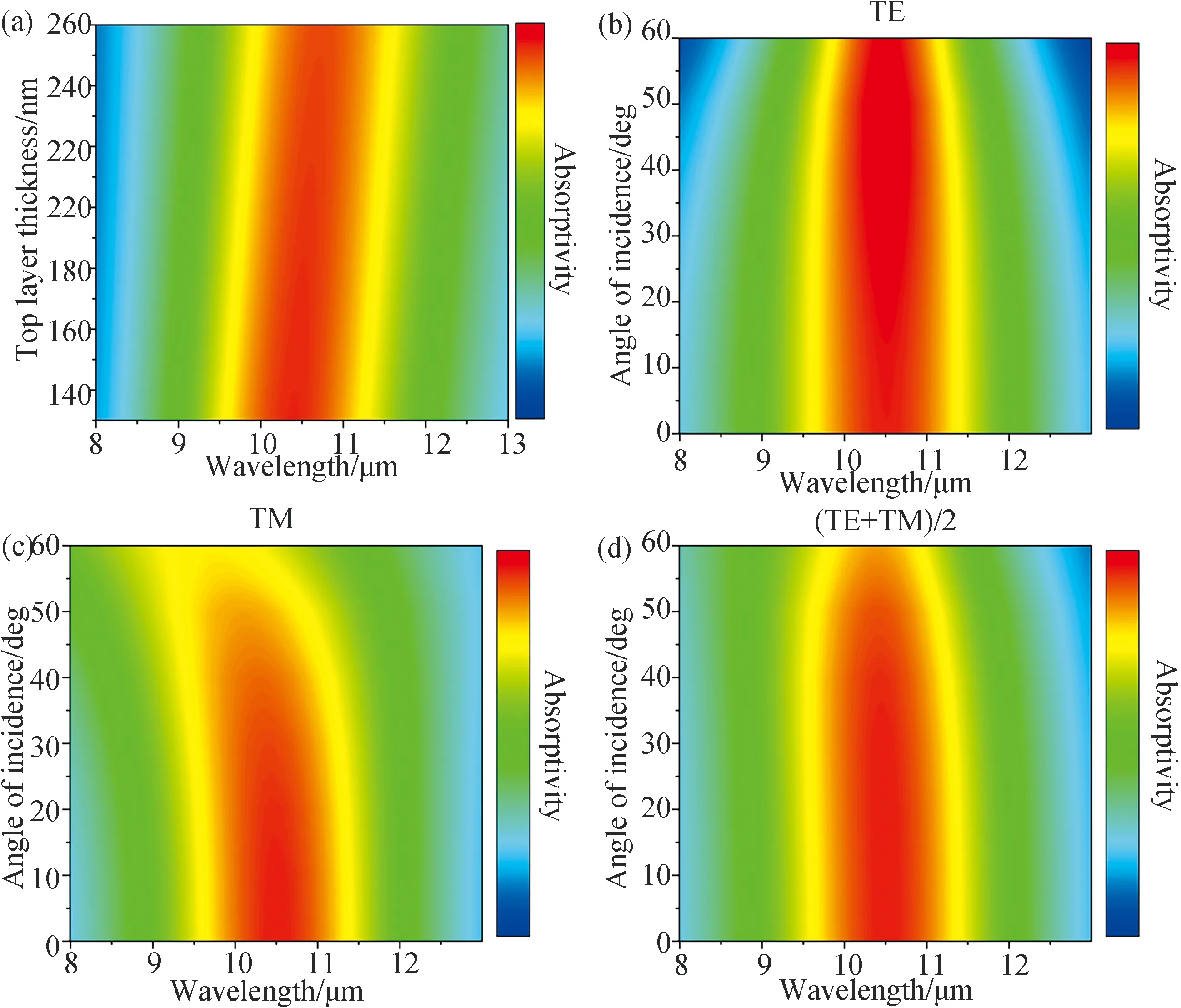
图5 顶层厚度和入射角对结构吸收性能的影响: (a)模拟计算的吸波器在顶层厚度H1不同的情况下的红外吸收率; (b)TE模式和(c)TM模式下入射角为0°到60°时的吸收图谱; (d)入射角不同时结构对TE和TM极化的平均吸收率(ATE+ATM)/2

在实际应用中, 入射角对结构吸收性能的影响同样值得探究. 如图5(b)～5(d)展示了入射角在0°到60°变化时, 结构在8～13 μm的吸收光谱. 无论是TE极化波(图5(b))还是TM极化波(图5(c)), 结构的吸收率都受到入射角的影响，但是受影响的情况不同. 对TE波而言, 结构的红外吸收率的最大值随着入射角增大的而变化, 当入射角为50°时, 结构的最大吸收率可达99.97%, 大于正入射时的94.93%. 吸收峰的位置并未发生明显移动, 仍约为10.5 μm. 而且随着入射角的增大吸收峰的带宽略有降低, 吸收大于70%的带宽由正入射时的2.46 μm下降为入射角为60°时的1.77 μm. 对TM波而言, 吸收性能随着入射角的增加而逐渐降低, 当入射角为60°, 结构的最大吸收率下降为81.95%, 且吸收峰的位置移动至9.57 μm. 因为红外摄像机同时接受TE和TM两种极化的辐射, 所以我们还计算了吸收器的TE和TM极化的平均吸收率((ATE+ATM)/2). 由图5(d)可知, 吸收器对TE和TM极化波的吸收率的平均值不敏感. 也就是说, 我们设计的结构的红外隐身性能对观测角度不敏感.

4 总 结

本文设计了一种利用简单的多层膜结构同时实现可调表面结构色颜色和可调红外吸收率的超材料吸收器. 通过将传输矩阵法和遗传算法结合, 完成了多层膜结构的优化设计. 设计的结构表面颜色可以通过改变顶层薄膜的厚度进行变化. 同时, 我们利用晶态和非晶态的GST在8～13 μm相差较大的介电常数性能, 通过改变GST的结晶状态，在单一结构中设计实现了吸收率从94.93%到9.19%的变化. 该结构能在红外及可见光两个波段独立地实现对电磁波的调控, 使其具有红外-可见兼容隐身的潜在应用. 对电磁隐身超材料的设计和实验制备具有指导和借鉴意义.