关于高斯最小值猜测的一个注记

钟扬帆， 马 婷， 胡泽春

(四川大学数学学院， 成都 610064)

Letn≥2 and (Xi,1≤i≤n) be a centered Gaussian random vector. The well-knownidk’s Inequality[1-2]says that

E(max1≤i≤n|Xi|)≤E(max1≤i≤n|Yi|)

(1)

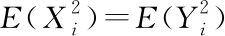
If we replace “max” by “min” inidák’s inequality, Gordonetal[3-4]. proved among other things that

(2)

E(min1≤i≤n|Xi|)≥E(min1≤i≤n|Yi|)

(3)

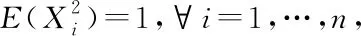
Now we state the main result of this paper.

Theorem1.1The Gaussian minimum conjecture holds if and only ifn=2.

The rest of this paper is organized as follows. In Section 2 and Section 3, we give the necessity proof and the sufficiency proof of Theorem 1.1, respectively. In the final section, we give some remarks.

2 Necessity proof of Theorem 1.1

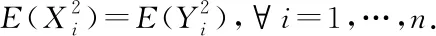
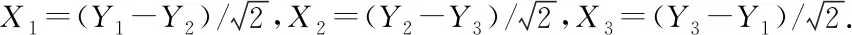
At first, we calculateE(min1≤i≤3|Yi|). The density functionp1(x,y,z) of (Y1,Y2,Y3) can be expressed by

By the symmetry, we have

(4)

Define a function

and a set

Define a transformation

Denote byDTthe original image ofDunderT.Then we have

DT={(u,v)∈R2:T(u,v)∈D}={(u,v)∈

Now, we have

(5)

By (4) and (5), we get

(6)

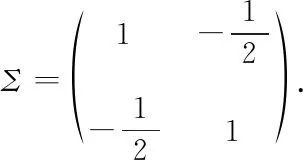
Then the density functionp2(x,y) of (X1,X2) can be expressed by

By the symmetry, we have

(7)

where

We have

It follows that

(8)

We have

It follows that

(9)

We have

It follows that

(10)

We have

(11)

By (7)～(11), we obtain

E(min1≤i≤3|Xi|)=

(12)

Hence we get

E(min1≤i≤3|Yi|)-E(min1≤i≤3|Xi|)=

(ii)n≥4. Without loss of generality, we only consider the case thatn=4. We use proof by contradiction. Suppose that (3) holds forn=4. LetYi,Xi,i=1,2,3 be the same as in the above example. LetY4be a standard Gaussian random variable independent of (Y1,Y2,Y3). Then, by the assumption, for anya>0, we have

E((min1≤i≤3|Xi|)∧|aY4|)≥

E((min1≤i≤3|Yi|)∧|aY4|).

Lettinga→∞, by the monotone convergence theorem, we obtain that

E(min1≤i≤3|Xi|)≥E(min1≤i≤3|Yi|).

It is a contradiction. Hence for anyM>0, there existsa0>Msuch that

E((min1≤i≤3|Xi|)∧|a0Y4|)<

E((min1≤i≤3|Yi|)∧|a0Y4|).

3 Sufficiency proof of Theorem 1.1

In this part, we will show that the inequality(3) holds ifn=2.WriteX1=x1f1,X2=x2f2, where bothf1andf2have the standard normal distributionN(0,1).Without loss of generality, we can assume thatx1,x2>0. Further we can assume thatx1=1,x2=a∈(0,1].

and thus the density function of (f1,af2) is

p(x,y)=

At first, we assume thatρ∈[0,1). By the symmetry, we have

E(|f1|∧|af2|)=

Define

Then

We have

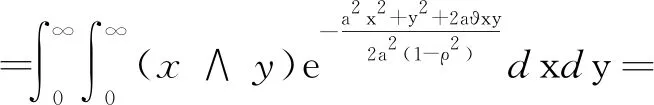
Define

whereα>0,β>0,αβ-γ2>0. Then we have

I(ϑ)=J(a2,1,aϑ)+J(1,a2,aϑ),

thus

[J(a2,1,aρ)+J(1,a2,aρ)+J(a2,1,-aρ)+

J(1,a2,-aρ)]

(13)

In the following, we come to calculate the functionJ(α,β,γ). We have

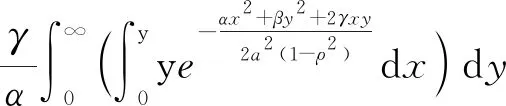
J1(α,β,γ)-J2(α,β,γ)

(14)

where

We have

J1(α,β,γ)=

(15)

J2(α,β,γ)=

(16)

By (14)～(16), we get

which together with (13) implies that

[J(a2,1,aρ)+J(1,a2,aρ)+J(a2,1,-aρ)+

(17)

Ifρ=1, thenf2=f1a.s.. Note thata∈(0,1]. Then we have

E(|f1|∧|af2|)=aE(|f1|)=

In addition, ifρ=1, we have

Hence (17) holds for anyρ∈[0,1].

For anya∈(0,1] and anyρ∈(0,1), we have

Hence for anya∈(0,1],

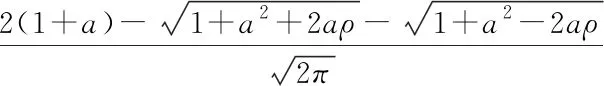
is a strictly increasing function inρ∈[0,1]. Hence it reaches its minimum value atρ=0,i.e. the inequality (3) holds.

4 Remarks

Remark1(i) Prof. Shao Qi-Man[9]told us that the Gaussian minimum conjecture forn=2 can be proved based on the following fact:

P(min(|X1|,|X2|)>x)=1-P(|X1|≤x)-

P(|X2|≤x)+P(|X1|≤x,|X2|≤x)≥

1-P(|X1|≤x)-P(|X2|≤x)+

P(|X1|≤x)P(|X2|≤x)=

1-P(|Y1|≤x)-P(|Y2|≤x)+

P(|Y1|≤x)P(|Y2|≤x)=

1-P(|Y1|≤x)-P(|Y2|≤x)+

P(|Y1|≤x,|Y2|≤x)=

P(min(|Y1|,|Y2|)>x)

(18)

where the Gaussian correlation inequality was used.

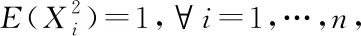
Remark2Forn≥3, we can’t obtain the corresponding inequality similar to (18) by using the Gaussian correlation inequality. In fact, these inequalities do not hold by the necessity result of Theorem 1.1.