考虑预应力孔道影响的连续刚构剪力滞效应研究

邬晓光,时元绪,鄢稳定,殷 悦

(长安大学 公路学院，陕西 西安 710064)

由于大跨连续刚构桥具有线形优美、刚度大、跨越能力强等特点，在国内应用极为广泛，而大跨连续刚构桥主要采用截面尺寸较大的箱形截面，具有较为明显的空间受力特点，在连续刚构悬臂浇注阶段和成桥阶段均会存在剪力滞效应，如果考虑不到位将会引起箱梁顶底板开裂，影响结构的使用寿命。

近几年，国内外学者对剪力滞效应的研究成果主要有：REISSNER[1]第一次采用能量变分法分析箱梁的剪力滞效应，并得到了翼缘板应力和挠度的解析解。随后诸多学者均采用该方法研究箱梁的剪力滞效应[2-4]；大量学者又提出了基于剪切变形规律的有限梁段法对剪力滞效应进行分析[5]。柳兴成[6]等利用受弯梁的截面不受轴力的静力平衡条件，推导出波形钢腹板箱梁在余弦剪滞翘曲位移函数下的附加轴力计算公式。时元绪[7]等基于阶梯型刚度模型推导了考虑损伤的刚度折减系数，提出了考虑主梁损伤的简支箱梁剪力滞计算方法。安平和[8]等采用有限元模型分析了配筋对装配式T梁剪力滞效应的影响。马庆华[9]等对箱梁悬臂施工中的预应力作用及剪力滞效应进行了研究。时元绪[10]等建立了实体有限元模型分析了装配式箱梁考虑配筋后的剪力滞效应。

对于大跨PC箱梁桥的分析中：孙志伟[11]等采用比拟杆法并结合肢解法研究了连续刚构宽箱梁的剪力滞效应，并求解了翼缘板的有效分布宽度。谭仕强[12]以一座大跨径叠合梁斜拉桥为研究对象，提出了一种基于三分析模型的有限元计算方法。文献[13-16]采用有限元软件分析了大跨径PC连续刚构桥的剪力滞效应。

虽然对连续刚构桥的研究较多，但是在连续刚构桥的悬臂浇筑过程中很少考虑预应力孔道对于剪力滞效应的影响，并且预应力孔道对于剪力滞效应的影响规律分析较少，因此本文采用实体有限元软件，重点分析了不同施工梁段中预应力孔道对于剪力滞效应的影响，并得到了预应力孔道的影响规律。

1 依托桥型概况

1.1 工程概况

本文以某座特大桥连续刚构作为本次计算分析的依托桥型。该桥梁的基本概况：桥梁跨径布置为(65+3×120+65)m变截面预应力混凝土连续刚构，桥梁总长为490 m，宽为：24.5 m[2×(0.5 m+净11.25 m+0.4 m)+2×0.1 m(中央分隔带)]。上部结构采用变截面预应力混凝土箱梁，下部结构采用空心薄壁墩和钻孔灌注桩基础。主梁整体布置如图1所示。

图1 连续刚构整体布置图(单位：cm)Figure 1 Overall layout of continuous rigid frame(Unit: cm)

1.2 设计概况

a.主要材料。

① 混凝土。

上部结构采用C55混凝土；桥墩采用C40混凝土；桥面铺装采用10 cm厚沥青混凝土+8 cm厚C50混凝土调平层。

② 钢材。

预应力钢绞线：低松弛高强度预应力钢绞线公称直径为ΦS为15.2 mm，公称截面面积A为140 mm2，钢绞线标准强度fpk为1 860 MPa，弹性模量EP为1.95×105MPa。

普通钢筋：纵向普通钢筋采用HRB400级钢筋，弹性模量Es为2.0×105MPa

b.上部结构设计。

该PC连续刚构桥，边中跨比为0.54，箱梁根部梁高为7.2 m，跨中及端部梁高为3.0 m，底板按1.8次抛物线变化；横截面采用单箱单室直腹板箱梁，箱梁顶板宽12.15 m，底板宽6.5 m，悬臂长度2.825 m。悬臂板根部厚度和端部厚度分别为75、20 cm，顶板厚度30～50 cm，底板厚度32～110 cm，腹板厚度为50～100 cm。

主墩支点和跨中典型截面尺寸如图2、图3所示。

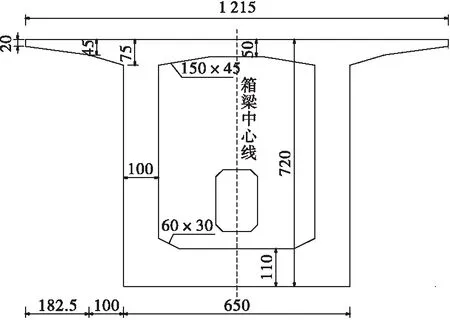
图2 主墩支点处典型横断面(单位：cm)Figure 2 Typical cross section at the fulcrum of main pier(Unit: cm)

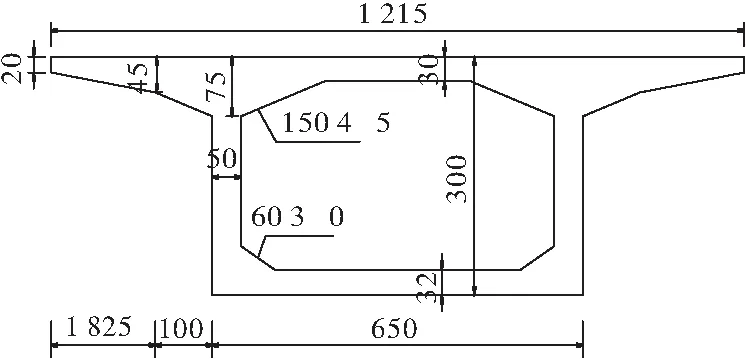
图3 跨中处典型横断面(单位：cm)Figure 3 Typical cross section at midspan(Unit: cm)

2 有限元分析悬臂浇注阶段剪力滞效应

由于每个“T构”均相同，在悬臂浇注施工阶段分析中仅分析1号墩所形成的“T构”，1号墩“T构”梁段编号和尺寸如图4所示，由于0、1、1′号块在托架上进行施工，分析时从2号块进行分析。

图4 1号墩T构示意图(单位：cm)Figure 4 Schematic diagram of T-structure of 1 Pier(Unit: cm)

本文分析悬臂浇筑过程中的最不利截面位置：悬臂梁根部附近(1号块、2号块)，分析截面如图5所示。

图5 应力值提取截面位置图Figure 5 Drawing of stress value extraction section location

由于在施工过程中“T构”为对称浇注，本文仅提取“T构”的一侧顶板应力值进行分析。选取1号墩边跨，每个梁段施工完成后均需要提取悬臂梁1号块中间截面A1、2号块中间截面A2。由于箱梁受力具有对称性，因此选取箱形截面一侧提取应力，具体应力点布置如图6所示。

图6 关键截面应力提取点位置图Figure 6 Key section stress extraction point location

2.1 Midas/Civil模型

为得到连续刚构桥内力分布和初等梁理论计算的应力值，采用Midas/Civil软件建立连续刚构桥有限元模型；由于剪力滞效应影响桥梁的纵向应力，因此该模型中主要考虑纵向普通钢筋、纵向预应力钢束，而忽略竖向预应力钢束、横向预应力钢束、构造钢筋及箍筋。悬臂浇筑阶段的荷载主要有自重、预应力荷载、挂篮荷载和湿重，其中挂篮重850 kN，采用节点荷载的形式作用于梁体上，通过节点荷载的钝化和激活来模拟挂篮前移。

1号墩T构最大悬臂浇筑阶段连续刚构桥有限元模型如图7所示，该模型一共有69个节点，66个单元，梁单元的长度根据施工梁段的长度来确定。在两个墩节点处采用固结，在墩与梁连接处采用弹性连接中的刚性。

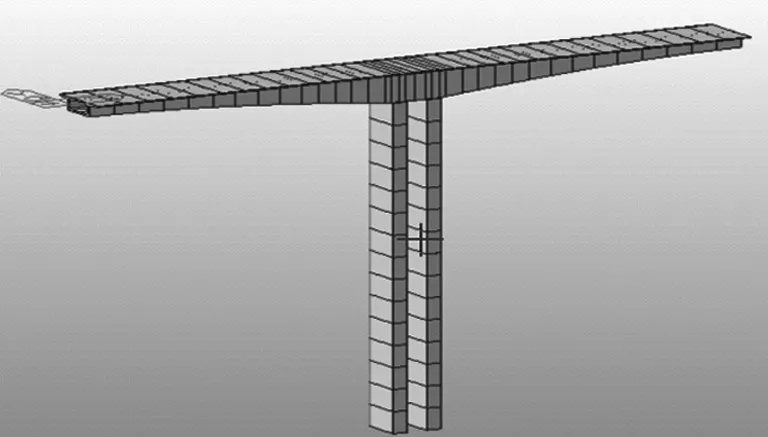
图7 1号墩T构有限元模型Figure 7 Finite element model of T-structure of 1 pier

2.2 Midas/Fea模型

为得到连续刚构桥的真实应力分布，本文采用实体有限元软件Midas/Fea建立连续刚构桥模型， 由于本次依托桥型共有14个施工梁段，由于该连续刚构桥的施工梁段较多，本文仅展示2号块施工工况的实体有限元部分模型如图8～图11所示。模型中将预应力钢束和普通钢筋划分为网格尺寸30 cm的线单元，将上部结构混凝土实体划分为网格尺寸为1倍内顶板厚度30 cm的六面体单元，无孔道模型一共划分81 657个节点，79 679个单元，有孔道模型一共划分128 645个节点，211 555个单元。墩底部采用固结，梁与墩连接处也采用固结。

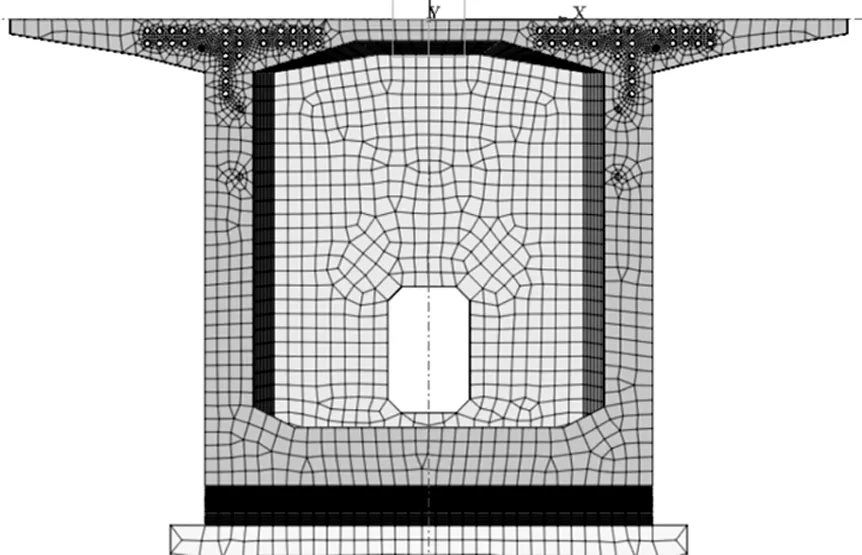
图8 0～1号块带孔道实体模型Figure 8 Solid model of 0 ～1 block with channel

图9 0～1号块预应力钢束网格图Figure 9 Grid diagram of block 0 ～1 prestressed steel tendon

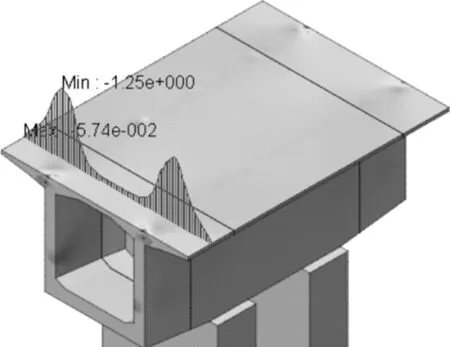
图10 A1截面无孔道顶板应力分布图(单位：MPa)Figure 10 Stress distribution map of A1 section roof without channel(Unit: MPa)

图11 A1截面有孔道顶板应力分布图(单位：MPa)Figure 11 Stress distribution map of A1 section roof with channel (Unit: MPa)

2.3 结果分析

根据上述应力提取截面和提取点，将得到的2号块施工工况的数据汇总如表1所示，并做成折线图如图12、图13所示。表格中的实体模型为Midas/Fea模型，梁格模型为Midas/Civil模型。

表1 2号块施工工况顶板正应力Table 1 Normal stress of roof under construction condition of 2 blockMPa位置孔道时间实体模型不同应力测点的正应力1234567梁格模型应力测点的正应力无孔道浇注后-0.057-0.401-0.726-1.22-0.702-0.469-0.098-0.815A1截面张拉后-1.019-1.419-1.986-2.654-2.483-2.338-2.338-2.179有孔道浇注后-0.065-0.421-0.86-1.568-0.855-0.481-0.108—张拉后-1.055-1.512-2.105-2.98-2.666-2.534-2.422—A2截面无孔道张拉后-0.048-0.153-1.21-1.245-1.793-1.101-0.792-1.036有孔道张拉后-0.063-0.172-1.35-1.585-1.899-1.118-0.825—

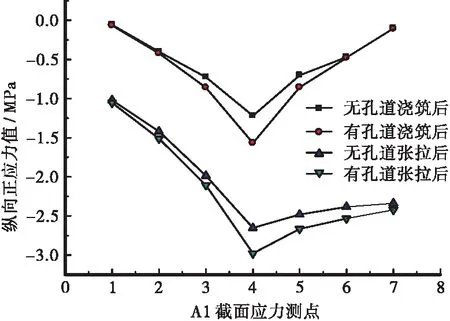
图12 2号块A1截面顶板正应力Figure 12 Normal stress of 2 block A1 section roof

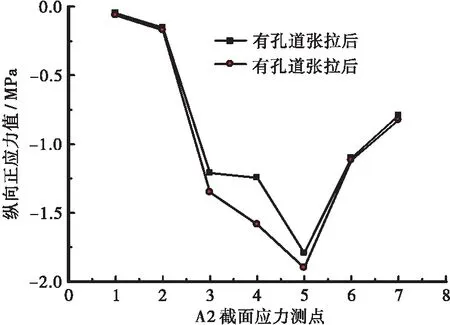
图13 2号块A2截面顶板正应力Figure 13 Normal stress of 2 block A2 section roof

根据表1中数据计算出剪力滞系数，本次提取的剪力滞系数为顶板正应力测点的最大值与梁格模型的正应力计算值之比，并分析有孔道与无孔道应力值，汇总成表2、表3。

表2 2号块顶板最大剪力滞系数Table 2 Maximum shear lag coefficient of 2 block roof位置时间孔道剪力滞系数增幅/%浇注后无孔道1.49728.417A1截面有孔道1.922张拉后无孔道1.21812.315有孔道1.368A2截面张拉后无孔道1.7315.893有孔道1.833

表3 2号块有孔道与无孔道顶板正应力对比Table 3 Comparison of normal stress between perforated and non perforated 2 block roof应力测点A1截面浇注后正应力A1截面张拉后正应力A2截面张拉后正应力差值/MPa增幅/%差值/MPa增幅/%差值/MPa增幅/%10.00814.040.0363.530.01531.2520.024.990.0936.550.01912.4230.13413.060.1195.990.1411.5740.34828.520.32612.280.3427.3150.15313.880.1837.380.1065.9160.0122.360.1968.380.0171.5470.0110.20.0843.590.0334.17

从表1～表3和图12、图13可知：

a.对于A1截面，无论浇注工况还是张拉工况，箱形截面中腹板处应力值远大于悬臂板端部应力值，为正剪力滞效应。

b.对于A2截面，箱形截面中应力最大值并不在腹板处，而在腹板右侧大约100 cm处，距离为内顶板的六分之一。

c.对于A1截面，无孔道模型中浇注工况和张拉工况最大剪力滞系数分别为1.497和1.218。

d.对于A2截面，无孔道模型中张拉工况最大剪力滞系数为1.731。

e.有孔道模型与无孔道模型计算结果有较大差异，有孔道模型由于截面被孔道削弱，应力值大于无孔道模型，差值在0.008～0.348 MPa范围内，在远离腹板处差值较小，而在腹板附近位置差值较大，在A1截面浇注工况下差值达到0.348 MPa，剪力滞系数从1.497增大到1.922，增幅为28.417%，其他截面剪力滞系数均增大，因此截面中孔道的存在将会加剧剪力滞效应。

根据上述分析思路，可依次分析剩下梁段，由于数据量较大，以下仅展示9号梁段的数据，应力分布如图14、图15所示。

图14 9号块A1截面顶板正应力Figure 14 Normal stress of 9 block A1 section roof

图15 9号块A2截面顶板正应力Figure 15 Normal stress of 9 block A2 section roof

为分析预应力孔道对于剪力滞效应的影响，计算出A1截面、A2截面的剪力滞系数，将计算结果汇总如表4所示。

表4 9号块顶板最大剪力滞系数Table 4 Maximum shear lag coefficient of 9 block roof位置时间孔道剪力滞系数增幅/%浇注后无孔道1.0920.49A1截面有孔道1.097张拉后无孔道1.1120.56有孔道1.118浇注后无孔道1.1231.706A2截面有孔道1.142张拉后无孔道1.091.277有孔道1.104

为分析预应力孔道对于翼缘板应力的影响，计算出A1截面、A2截面的无孔道与有孔道模型中的应力增加幅值，将计算结果汇总如表5所示。

表5 9号块有孔道与无孔道模型顶板纵向正应力对比Table 5 Comparison of longitudinal normal stress between perforated and non perforated 9 block roof应力测点A1截面浇注后正应力A1截面张拉后正应力差值/MPa增幅/%差值/MPa增幅/%1-0.0240.34-0.0350.432-0.0570.76-0.0780.893-0.1321.61-0.1071.134-0.1711.93-0.161.565-0.1341.48-0.121.146-0.0630.69-0.070.667-0.0450.49-0.060.56应力测点A2截面浇注后正应力A2截面张拉后正应力差值/MPa增幅/%差值/MPa增幅/%1-0.0320.45-0.0360.422-0.0670.93-0.5366.563-0.121.66-0.121.394-0.1732.19-0.1631.755-0.1411.71-0.1241.286-0.0690.84-0.0810.847-0.0350.43-0.0470.49

从表4、表5和图14、图15可知：

a.对于A1截面，从悬臂板端部向腹板位置处增长速度较快，然后从腹板到顶板中心处应力值增长速度减缓，在顶板中心处取得最大值。

b.对于A2截面，箱形截面中应力最大值并不在腹板处，而在腹板右侧大约100 cm处，距离为内顶板的六分之一。

c.对于A1截面，无孔道模型中浇注工况和张拉工况最大剪力滞系数分别为1.092和1.112。

d.对于A2截面，应力值均小于A1截面，说明越靠近悬臂梁根部受力越大，无孔道模型中浇注工况和张拉工况最大剪力滞系数分别为1.123、1.09。

e.有孔道模型与无孔道模型计算结果差异较小，有孔道模型由于截面被孔道削弱，应力值大于无孔道模型，差值在0.024～0.173 MPa范围内，在远离腹板处差值较小，而在腹板附近位置差值较大，在A1截面浇注工况下差值达到0.171 MPa，剪力滞系数从1.092增大到1.097，增幅为0.49%，其他截面剪力滞系数均稍有增大，但幅度相比于前面的梁段更小，截面孔道对于剪力滞效应的影响基本上很小。

将所有施工阶段的A1截面的剪力滞数据进行汇总，并根据箱梁截面的对称性，将应力测点扩展到全截面，将剪力滞系数与顶板纵向应力汇总如图16、图17。

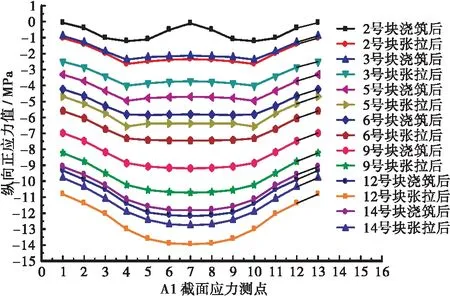
图16 不同施工梁段A1截面应力测点Figure 16 Stress measuring points of A1 section of different construction beam sections

图17 不同施工梁段A1截面最大剪力滞系数Figure 17 Maximum shear lag coefficient of A1 section of different construction beam sections

3 结语

a.对于A1截面，从2号块到5号块，应力值从悬臂板端部向腹板处逐渐增大，增幅较大，从腹板到顶板中心处逐渐减小，增幅较小，表现为正剪力滞效应；从5号块以后，顶板中心处的应力值开始大于腹板处，并逐渐增大。总体来说，随着梁段施工的不断进行，顶板纵向应力值的峰值从腹板处逐渐向中心处转移。对于A2截面，随着梁段施工的不断进行，顶板应力最大值均出现在距腹板处大约b/3处，其中b为内顶板的一半。

b.有孔道模型的顶板应力值均大于无孔道的应力值。随着施工过程的进行，预应力孔道对于应力的影响越来越小，在前7号块施工时差值均大于0.2 MPa，尤其2号块浇注后达到了0.348 MPa，预应力孔道的存在会加剧剪力滞效应，最大增幅达到了28.4%，而8号～14号块施工时，预应力孔道对于顶板应力的影响基本上可以忽略。

c.通过有限元分析得到了悬臂浇注阶段不同施工阶段最不利截面应力分布特点和剪力滞系数变化规律，随着梁段不断浇注，剪力滞系数逐渐减小，在施工到6号块时趋于稳定，基本上在1.1左右。