冰雪环境双车道公路弯道车速特征及预测模型

吕 惠， 管星宇， 陈彦旭， 袁 方

(1.上海市城市建设设计研究总院(集团)有限公司， 上海 200125; 2.上海市政工程设计研究总院(集团)有限公司， 上海 200092； 3.同济大学 道路与交通工程教育部重点实验室， 上海 201804)

1 概述

我国三、四级公路与等外公路占公路总里程的85%以上[1]，与高等级公路相比，低等级公路技术指标相对较低，平面线型复杂，特别是调研表明山区低等级公路频繁设置小半径平曲线，行车安全受较大影响[2]。车辆在通过此类弯道路段时，往往会产生较大的离心力，在冰雪天气下，道路表面的附着系数急剧降低，路面与轮胎无法提供车辆在正常天气下行驶的摩擦力，驾驶人对车辆的操控水平下降，驾驶负荷上升，在极端情况下可能发生横向滑移，进而导致车辆失控，引发事故。WANG[3]等对国外事故的统计分析发现，弯道事故率是直线路段的3倍以上。美国国家公路交通安全管理局[4](NHTSA)公布的事故报告指出，潮湿路面发生车辆冲出路外事故的概率比干燥时增加1.8倍，冰雪路面则增加7倍。因此冰雪天气弯道路段发生事故的风险较高。

由于在冰雪天气弯道路段进行自然驾驶实验难以确保实验安全，因此国内外对于此类场景下车速预测模型的研究仍然较少，现有研究主要以正常天气为背景。较多研究结果表明平曲线的行驶车速主要与圆曲线半径有较强相关性，进而对平曲线运行车速进行建模，并以此作为道路线型连续性与一致性评价的参考依据[3,5-6]，我国《公路项目安全性评价规范》[7]中通过预测运行车速对行驶安全进行评价也是基于此类研究。ZHANG[8]等考虑了不同驾驶人的驾驶风格差异性，使用带遗忘因子的递推最小二乘法构建弯道车速模型。LI[9]等提出了一种平曲线路段超速警告系统，平曲线安全车速的计算与道路曲率、道路表面摩阻系数等因素有关。FITZSIMMONS[10]等基于线性混合效应模型构建了城市、农村道路的弯道车速及轨迹预测模型，结论表明入弯时的车速及车辆横向位置对弯道内车速、轨迹有显著影响。随人工智能的发展，也有研究使用BP神经网络对弯道车速进行预测[11-12]，取得了一定成果。

为重点研究冰雪天气下弯道路段车速特征并构建相应预测模型，本研究借助同济大学8自由度驾驶模拟器进行单车驾驶模拟实验，仿真场景对真实驾驶环境的还原程度高，在解决驾驶实验安全性问题的同时，保证了实验数据的有效性，研究结果对于冰雪天气危险驾驶行为研究及制定限速等管理策略均有指导意义。

2 实验设计

2.1 研究变量

为研究冰雪天气下平曲线路段的车速变化规律并构建预测模型，文本选取的主要研究变量分为两类。第一类为驾驶环境变量，包括天气环境、圆曲线半径、转向；第二类为行驶车速。

环境变量主要针对冰雪天气，同时考虑正常天气环境作为对比，因此共设置晴天、雨天、雪天、结冰4种场景，冰雪对弯道行驶安全的影响主要为路面附着系数f的降低，参考现有研究成果[13]，不同天气对应的f取值如表1所示。

表1 路面附着系数Table 1 Coefficient of road adhesion天气环境f经验值f取值晴天0.65～0.850.8雨天0.46～0.640.5雪天0.26～0.450.3结冰0.10～0.250.2

双车道公路通常为低等级公路，考虑到冰雪环境，最大超高取6%，圆曲线半径设置参考《公路路线设计规范》[14]中20～60 km/h设计车速范围内各级车速对应的圆曲线最小半径极限值，确定为15、35、60、135、270 m。

车速变量选用平曲线5个要素点位置的车速，如图1所示，以及圆曲行驶过程中的平均车速。

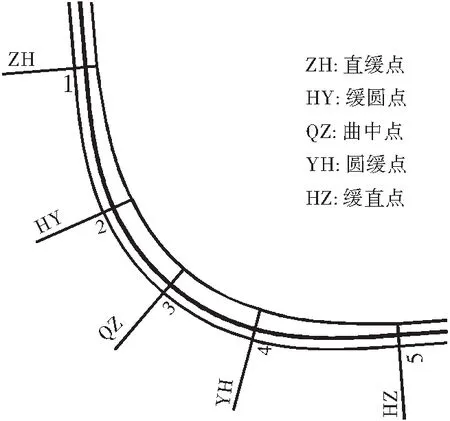
图1 车速采集点Figure 1 Collection points of vehicle speed

本文研究过程中使用的全部变量与对应描述见表2。

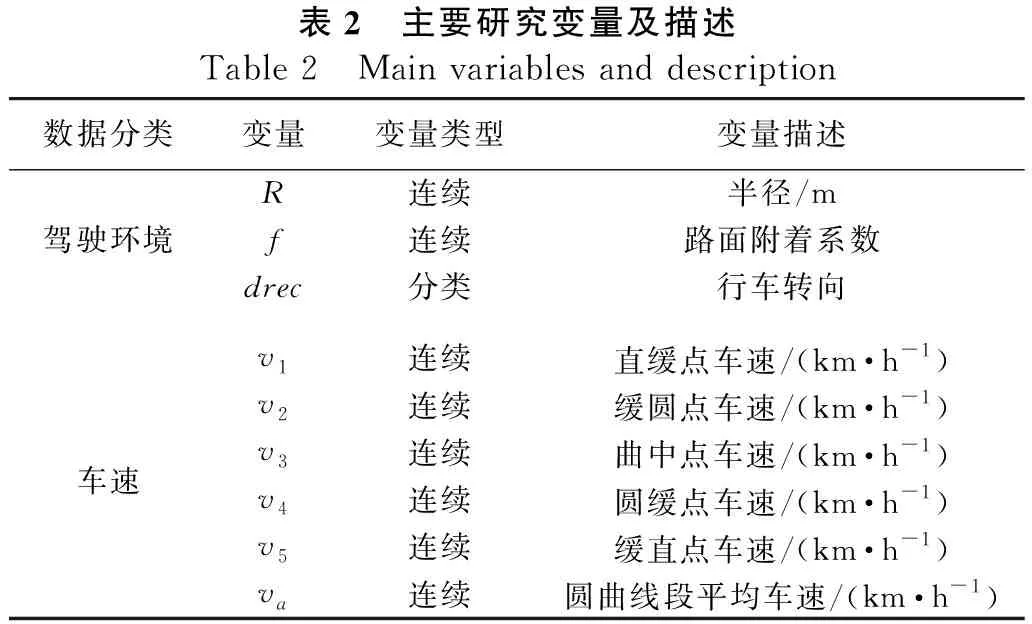
表2 主要研究变量及描述Table 2 Main variables and description数据分类变量变量类型变量描述R连续半径/m驾驶环境f连续路面附着系数drec分类行车转向v1连续直缓点车速/(km·h-1)v2连续缓圆点车速/(km·h-1)车速v3连续曲中点车速/(km·h-1)v4连续圆缓点车速/(km·h-1)v5连续缓直点车速/(km·h-1)va连续圆曲线段平均车速/(km·h-1)

2.2 实验设备

本研究采用同济大学8自由度驾驶模拟器完成实验，驾驶模拟器由驾驶舱、液压系统与底部运动系统组成，如图2所示，驾驶舱受液压系统推力在空间中有6个自由度，底部平动系统有2个自由度。驾驶舱内部配有一辆无引擎的1∶1实车，顶部安装有5台投影仪，并与环形幕布构成成像系统，如图3所示。

图2 8自由度驾驶模拟器Figure 2 8 Degrees of freedom driving simulator

图3 驾驶模拟器内部Figure 3 Interior of driving simulator

实验过程中设备可采集车速、路面附着系数、横向位置、道路半径、转向等数据，采样率设定为10 Hz。

2.3 实验场景设计

道路仿真场景按天气环境共分4个子路段，天气及相应的附着系数为无序布置，每个子路段线形指标相同，均包含前文所述的5组不同半径构成的平曲线，如图4所示，实验道路全长约7.6 km。

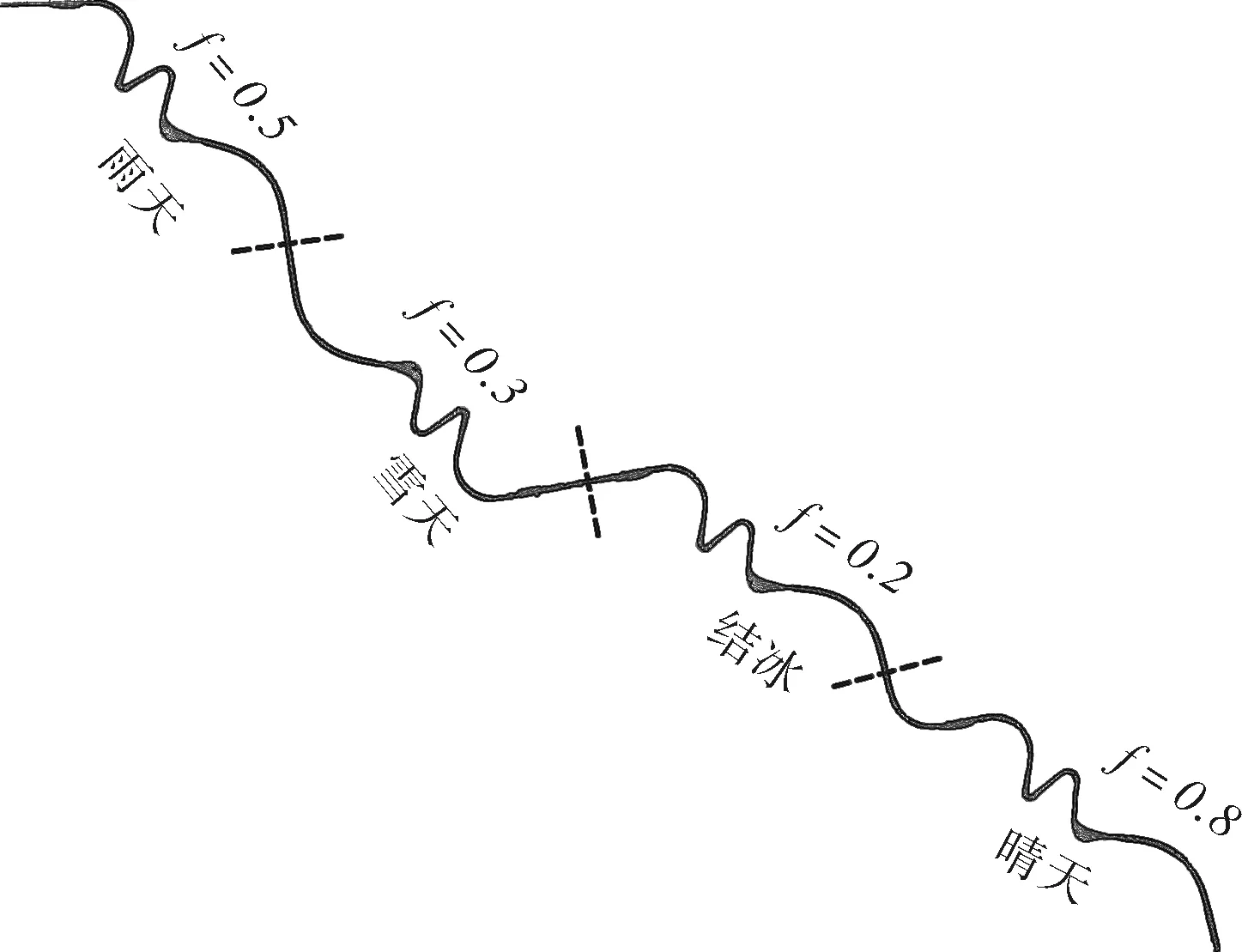
图4 驾驶模拟实验道路平面设计Figure 4 Road plane dsign for simulated scenario

道路横断面为标准7.5 m宽双车道，圆曲线超高、加宽均参照规范值设置，本研究主要针对弯道路段，为减小道路纵坡对实验的影响，纵坡设置为0。图5为使用道路设计软件及模拟驾驶软件构建的仿真场景。

晴天

2.4 实验人员

被试者共32名，均持有C1驾驶证，驾龄在3～12 a之间，平均驾龄为5.4 a；年龄在25～47岁之间，平均年龄为31.6岁。

2.5 实验过程

由于驾驶模拟器对冰雪天气的仿真与真实环境仍存在一定差别，在进行正式实验前，首先让被试者在试验路段行驶以获得湿滑路面的模拟驾驶体验，最大程度保证实验可靠性。考虑到驾驶人过弯时车速为自主选择行为，且因部分低等级公路缺乏限速设施，因此实验过程仅提示驾驶人山区公路注意控制车速，不宜超过60 km/h，保证驾驶安全。排除部分无效数据后，实验过程中共获取了589组弯道行驶的有效数据。

3 弯道车速特征

3.1 不同驾驶场景下弯道车速的分布规律

为分析车速在不同驾驶环境下的变化特征，在驾驶模拟实验获得的所有数据中，以各圆曲线路段的平均车速va作为代表车速，将va关于R、f的变化情况绘制于图6等高线图中(已平滑处理)。

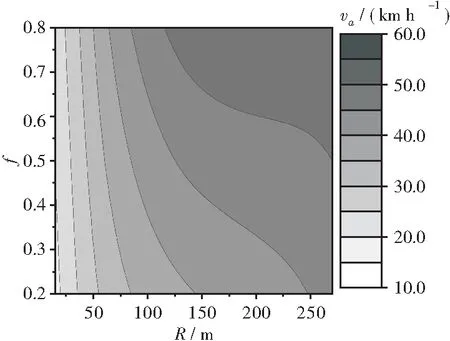
图6 平均车速在不同驾驶场景下的分布Figure 6 Distribution of average speed in different driving scenarios

观察车速分布的整体趋势可以发现，圆曲线路段的行驶车速随附着系数升高、半径增加而逐步增大，在R=270 m、f=0.8时，过弯的平均车速达到50 km/h，而在R=15 m、f=0.2的极端条件下，平均车速会降低至20 km/h以下。此外，随半径减小，摩擦系数对车速的影响逐渐下降，说明圆曲线半径对过弯车速的影响相对更大。

3.2 弯道内的车速变化规律

通过分析平曲线要素点对应的车速，在R≤60 m时，车速存在明显的减速段与加速段，整体呈现U型的变化规律，车速极小值一般出现在曲中点至圆缓点间；当R≥135 m时，车速的减速段与加速段不再明显。冰雪天气下弯道内的行驶车速明显低于晴雨天气，且普遍低于极限最小半径对应的设计车速，如图7所示。

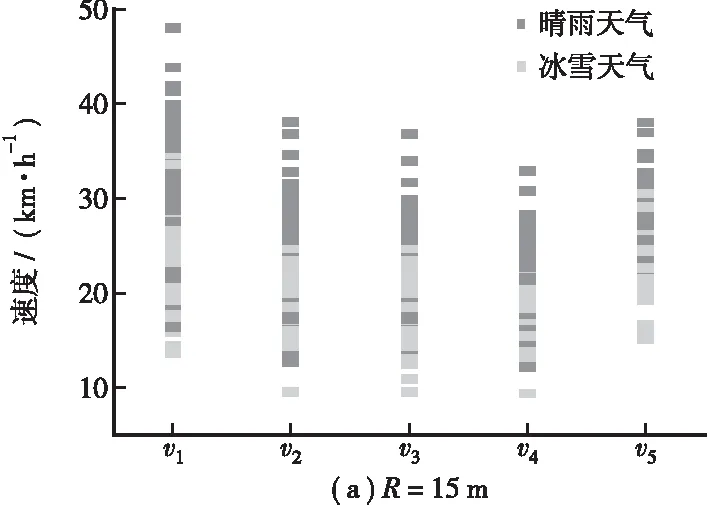
图7 平曲线上各要素点车速的变化规律

4 主要变量分析

4.1 偏相关性分析

对可能影响车速的主要变量进行Pearson偏相关性分析，表3为各圆曲线va与R、f、drec的偏相关性分析，结果表明圆曲线路段的平均车速与圆曲线半径相关性最高，其次为路面附着系数，与转向相关性较低。

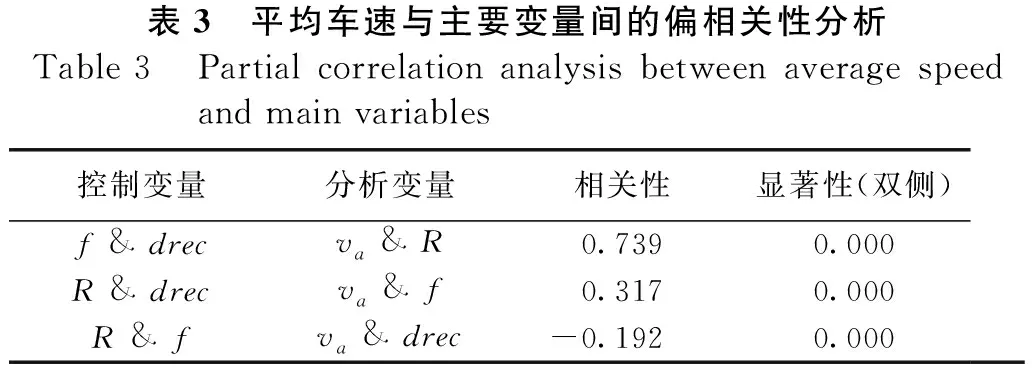
表3 平均车速与主要变量间的偏相关性分析Table 3 Partial correlation analysis between average speed and main variables控制变量分析变量相关性显著性(双侧)f & drecva & R0.7390.000R & drecva & f0.3170.000R & fva & drec-0.1920.000

4.2 车速与半径的曲线关系

通过SPSS曲线估计分析va与R的数学关系如下:F统计量显著性为0.000,小于0.05;拟合优度R2=0.621；F为1 011.416；确定va与R呈对数增长的关系，与以往研究结果基本一致[7,15]。

以va为纵坐标，R为横坐标，绘制所有车速样本的散点图与对数拟合曲线，结果如图8所示。

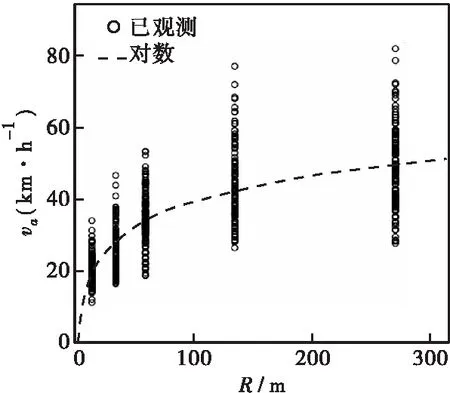
图8 散点图与对数曲线拟合Figure 8 Scatter and logarithmic curve fitting

分别对晴雨、冰雪天气下va、v1～v5与半径的关系进行相同分析，结果表明不同场景下平曲线上各点车速都与半径呈对数增长的关系，且相互间存在较强的线性相关性。

4.3 车速在不同附着系数下的分布差异

以va代表圆曲线路段行驶车速，不同附着系数下样本的正态性检验与方差检验表示各组样本均不满足正态分布与方差齐性，因此使用Kruskal-Wallis秩和检验对各组样本的差异性进行判断，结果表明va在不同附着系数下的分布有显著差异，如表4所示。

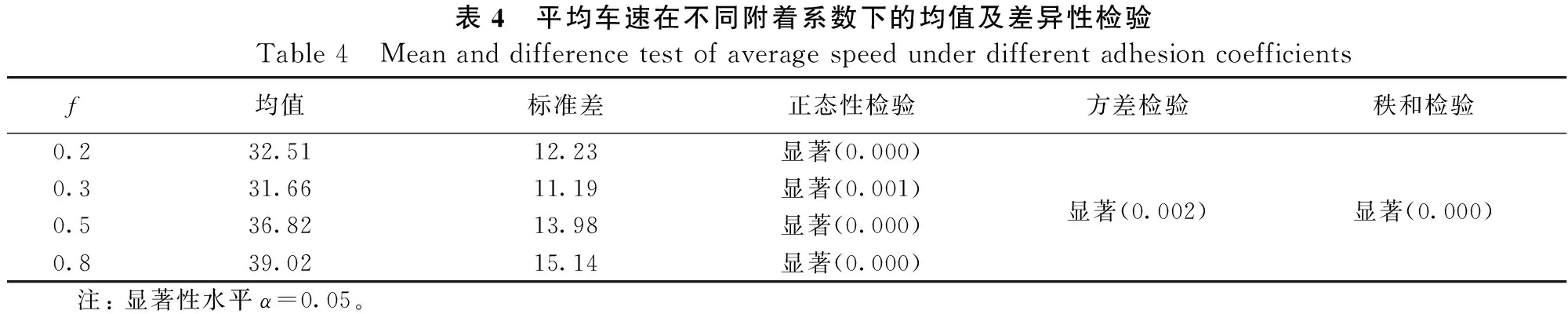
表4 平均车速在不同附着系数下的均值及差异性检验Table 4 Mean and difference test of average speed under different adhesion coefficientsf均值标准差正态性检验方差检验秩和检验0.232.5112.23显著(0.000)0.331.6611.19显著(0.001)显著(0.002)显著(0.000)0.536.8213.98显著(0.000)0.839.0215.14显著(0.000) 注: 显著性水平α=0.05。

进一步分析平均车速在4类附着系数下的组间差异，对平均车速进行平均秩检验，结果如表5所示，在4类附着系数下共有2个子集，分别为冰雪与晴雨场景，2个子集间存在较大统计学差异，而子集内部平均秩检验显著性大于0.1，表示子集内差异性小。因此，车速分别在冰雪、晴雨2个组合场景之间表现出较大差异，应分别在冰雪、晴雨2个组合场景中构建车速预测模型。

表5 平均车速的齐性子集Table 5 Homogeneous subsets of average speed子集不同附着系数样本0.20.30.50.8检验统计量调整后的显著性(双侧)1260.115266.5590.1010.9382318.800341.0201.2060.470

4.4 车速在不同转向下的分布差异

使用Kruskal-Wallis秩和检验对平均车速在不同转向下的差异性进行分析，结果表明车速在不同转向下无显著差异，如表6所示，同时结合表3分析结果，可知车速与曲线转向的相关性较低，因此预测模型不考虑将转向作为预测变量。

表6 平均车速在在不同转向下的均值及差异性检验Table 6 Mean and difference test of average speed under different driving directionsdrec均值标准差正态性检验方差检验秩和检验右转33.212.53显著(0.002)显著(0.029)不显著(0.151)左转30.9710.75显著(0.000)注: 显著性水平α=0.05。

5 平曲线车速预测模型

5.1 模型构建

(1)

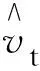
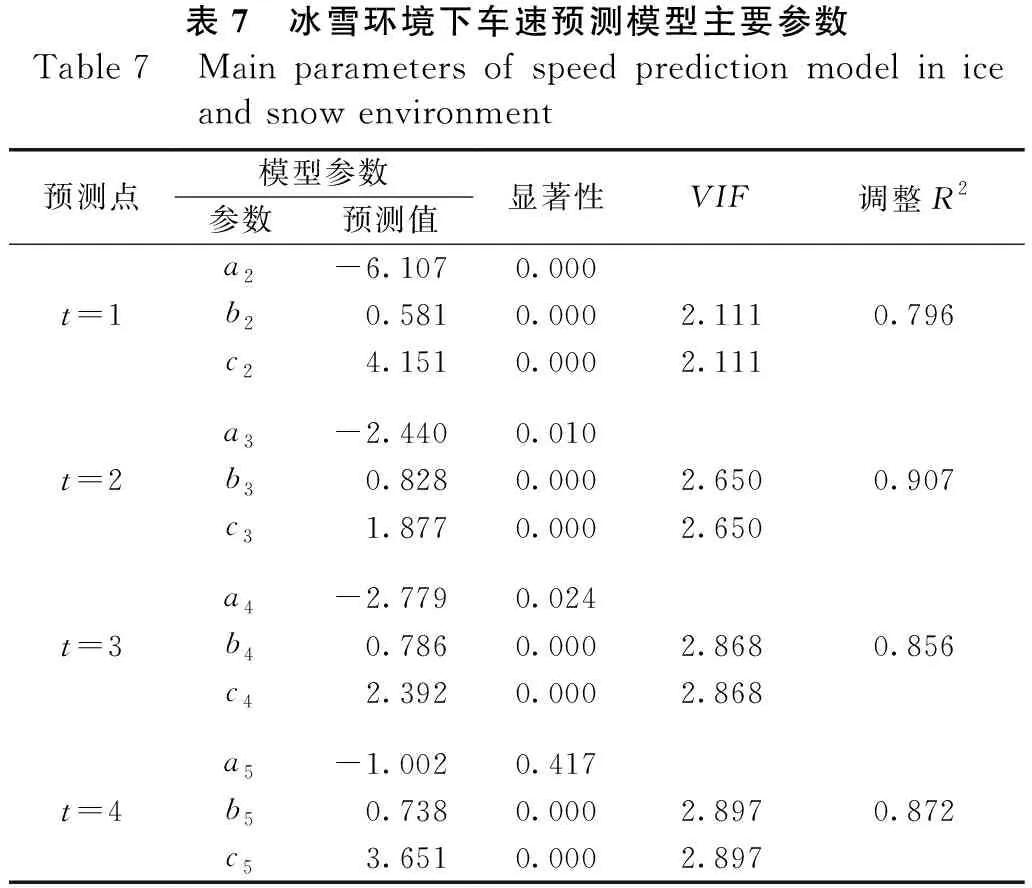
表7 冰雪环境下车速预测模型主要参数Table 7 Main parameters of speed prediction model in ice and snow environment预测点模型参数参数预测值显著性VIF调整R2a2-6.1070.000t=1b20.5810.0002.1110.796c24.1510.0002.111a3-2.4400.010t=2b30.8280.0002.6500.907c31.8770.0002.650a4-2.7790.024t=3b40.7860.0002.8680.856c42.3920.0002.868a5-1.0020.417t=4b50.7380.0002.8970.872c53.6510.0002.897

对模型的自变量显著性进行独立样本T检验，表中结果均小于0.05，说明自变量对预测车速具有显著影响，使用方差膨胀因子VIF检验自变量共线性，表中VIF<5，表示自变量间不存在共线问题，结合调整后的R2对模型拟合优度进行评价，由R2>0.7可知各点车速回归精度较好。

在获得平曲线上各要素点车速预测结果后，本文假设车速为连续均匀变化，各要素点间的车速以三次方样条插值确定。

5.2 模型检验

设实验中任一平曲线共有n个行驶车速采样点，以平曲线路段的平均误差率CMER(Curve Mean Error Rate)对平曲线车速预测模型的精度进行评价，如式(2)所示：

(2)

当车辆以较高速度行驶时，单独使用CMER无法完全体现预测精度，因此还需结合预测值与实际值的曲线相关系数对模型进行综合评价，通过matlab对模型与实际值的相关系数进行计算，得到本模型的总体相关系数为0.618。综合分析表明，模型具有一定适用性。

6 结语

a.车辆在曲线路段的行驶车速随半径增加、路面附着系数增大而增大，在平曲线行驶过程中，存在明显的减速段与加速段，车速极小值通常位于曲中点至圆缓点之间。

b.冰雪环境下，驾驶人趋于保守，车辆在弯道内的行驶车速明显低于晴雨天气，且普遍低于极限最小半径对应的设计车速。

c.圆曲线行驶车速与半径呈对数增长关系，与转向无明显相关性，各要素点的车速之间存在较强线性相关性。