基于CFD的离心式水泵流场分析及性能预测

程 鑫,张卫超

(1.武汉理工大学 机电工程学院，湖北 武汉 430070;2.湖北省磁悬浮工程技术研究中心，湖北 武汉 430070)

离心式水泵在工业生产生活中有着广泛的应用，性能预测是水泵设计中的重要环节，通过多次性能预测和分析以检验设计的优劣，再有针对性地进行设计优化，不断提高水泵性能，最终达到设计要求。水泵的性能预测方法主要有3种：损失模型法、神经网络法和流场分析法[1-2]。

损失模型法是针对水泵内不同的损失建立不同的数学模型，最后根据基本方程预测离心泵设计工况下的性能特性。姬亚亚[3]针对单级单吸离心泵，综合叶轮水力损失、容积损失和机械损失建立水力损失模型，预测的扬程与试验扬程之间的误差在5%之内，但是对于效率和轴功率的预测还存在一定误差。损失模型法能全面考虑水泵内部不同结构引起的能量损失，在水泵的设计工况范围内能较准确预测性能，偏离设计工况的预测值偏差较大[4]。

神经网络法在泵的性能预测方面的应用技术研究较多。传统的神经网络算法泛化能力差、收敛性差，导致预测结果准确度不高。李君等[5]提出小波神经网络方法，针对轴流泵建立其数学模型，并通过试验对比证明了性能预测结果的准确性和稳定性。孔琳[6]提出了一种基于改进BP神经网络算法，提高了计算的收敛性，应用在离心泵的性能预测中有较高的准确度和预测效率。神经网络的建立需要选取大量优秀的模型作为训练样本，足够多的样本训练后才能得到误差范围内的预测结果。

流场分析法是利用计算流体力学(computational fluid dynamics, CFD)对流体流动进行数值模拟，得到流场各个位置上的物理量的分布，从而建立泵内部流场特征和泵外特性之间的关系，分析影响泵性能的因素。随着计算机技术的发展和大量CFD商业软件涌现，流场分析法的应用日益广泛，对于离心泵这样的复杂流动计算也有较高的求解精度和效率[7]。王业芳等[8]采用流场分析法对低比转速离心泵进行数值计算，分析了在小流量工况下的压力脉动特性。聂小林[9]利用Fluent软件对多级离心泵内部的湍流流场进行了数值模拟，预测的性能曲线与实验的性能曲线较为一致。

笔者以离心式电子水泵为例，基于Solidworks构建其流道的三维模型，采用Fluent软件设计内流场模型并划分了非结构化网格，模拟分析水泵内部三维流场不同转速下、不同流量下的流体特征，以预测水泵在不同工况下的性能。

1 基础流场模型

冷却液在电子水泵中的流动是不可压缩的、粘性的湍流流动，其流动规律符合计算流体力学的基本控制方程，即连续性方程、动量方程和能量守恒方程。连续性方程也称为质量守恒方程，描述的是质量守恒定律；动量守恒方程在流体力学中，可以描述为流体微元中的动量等于其受到的各种力之和与作用时间的乘积[10-11]。

离心泵的流场模拟一般选用k-ε湍流模型。k-ε湍流模型适用范围广，在旋转流体域、漩涡及局部过渡流的计算中优势明显，能较好地反映离心泵内液体的流动情况[12]。

2 三维模型建立和网格划分

2.1 水泵的三维模型

电子水泵一般采用无刷直流电机驱动，其电机输出轴与叶轮直接连接，减少传动力矩损失。电子水泵的结构如图1所示，电机控制器为无刷直流电机的核心部分，连接定子绕组，产生不同大小不同方向的磁场控制定子转动，连接在转子末端的叶轮随之转动，叶轮达到一定转速后将水体从蜗壳的入水口吸入，从蜗壳出水口甩出。

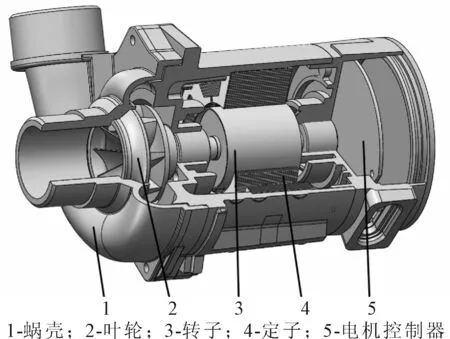
图1 电子水泵三维模型

2.2 计算流体域的选取

基于ICEM-CFD软件，选取水泵内部的流体域，为了方便仿真计算，将水泵内部流体域做必要的简化处理。根据水泵过流部件的结构特点,可以将水泵内部流场分为3个流体域：入口流体域、叶轮流体域和蜗壳流体域，其三维模型如图2所示。

图2 水泵内流体域的三维模型

2.3 网格划分

2.3.1 网格类型的选择

网格主要分为结构化网格和非结构化网格两个大类。结构化网格数据结构简单，网格生成质量好、速度快，但是不适用于求解复杂性较高的模型；非结构化网格内分布不均匀，但是适应性强，在复杂性较高的模型中，依然能够求解。

水泵的蜗壳流体域为三维曲面非对称造型，不利于结构化网格的生成，而叶轮流体域较多叶片的夹角更适用非结构化的网格。

2.3.2 网格划分

在ICEM-CFD软件中，单独对水泵的每一个流体域进行非结构网格划分。为提高网格生成质量，考虑到蜗壳夹角部位和叶轮的叶片处可能生成尖角、小面，网格质量较低，不利于后期的计算，需要在这些部分进行适当的网格加密，可以通过生成线网格和面网格来改善网格质量。

2.3.3 网格无关性验证

CFD方程的求解过程是将连续的物理量离散为有限个网格节点，离散过程必然存在一定的离散误差，网格的数量和质量都会直接影响求解的误差。在一定范围内，网格的数量越多，计算仿真结果的精度越高，但是求解时间也会越长[13]。网格数量过少，必然导致计算结果误差大，甚至无法收敛。网格的无关性验证，即验证用于计算的网格数量能满足精度条件。为了提高计算的工作效率，应在满足精度条件下，适当减少网格数量。

为了验证网格无关性，设计了5个网格划分方案，分别在Fluent求解器中计算。在相同的工况下，各个网格方案的预测水泵扬程结果如图3所示。当网格数量大于500万后，计算数值的变化均低于0.3%。为兼顾计算效率，选择网格方案3作为本次CFD计算的网格，各流体域的网格数分别为：入口流体域434 732，叶轮流体域1 263 688，蜗壳流体域2 497 695，总网格数量为41 963 089。

图3 不同网格方案的扬程预测结果

3 基于Fluent水泵计算模型

3.1 湍流模型的选择

车用电子水泵的作用是输送发动机冷却液，冷却液在水泵内的流动可认为是不可压缩的粘性湍流流动。常用的k-ε湍流模型适用范围广，在旋转流体域、漩涡及局部过渡流的计算中优势明显[14-15]，选择Standardk-ε湍流模型，能较好地反映泵内冷却液的流动情况。

3.2 边界条件设置

叶轮流体域为旋转区域，转速为4 200 r/min，入口流体域和蜗壳流体域均为静止区域。一共有2个交界面，入口流体域出口面和叶轮流体域的入口面为交界面，叶轮流体域的入口面和蜗壳的入口面为交界面。

3.3 压力速度耦合算法

Coupled算法对于求解可压缩流动问题以及在求解设计浮力或旋转运动的不可压缩流动上具有优势。亚松弛因子用于控制求解稳定性及收敛过程，该参数越大，迭代中物理量的变化越大。文中亚松弛因子设置取默认值。

3.4 收敛条件设置

由于该水泵的设计工况流量较小，计算残差值很难全部达到残差标准，因此还需要检测泵内流体域的其他物理量以判断收敛性。添加对水泵入口压力值变化、出口压力值变化和进出口水体质量之和3个物理量进行监控，当水泵出入口的压力值都达到稳定时，进出口的质量之和趋于零时，即可认为该计算达到收敛条件，出入口压力值、出入口水体质量之和监控曲线如图4和图5所示。

图4 出入口压力值监控曲线

图5 出入口水体质量之和监控曲线

从图4和图5可知，迭代计算在400次以后逐渐趋于平稳，虽然残差值还没有全部达到残差标准，但是出入口的水体质量之和趋近于零，入口压力一直稳定在101 kPa，出口压力逐渐稳定在137 kPa，计算结果已经收敛。

4 流场分析及性能预测

4.1 压力场分析

叶轮的高速转动使水泵入口处形成负压区，液体进入水泵后被叶片甩在蜗壳压水室内，液体在此过程中获得动能和压力能，进而沿着扩散管流出。从图6可知，水泵内流场的压力由入口到压水室，逐渐增加，从压水室到出口由于流动损失，压力缓慢较小，整体压力分布较为均匀。蜗壳的隔舌处为明显的高压区，当流量较小时，该区域较小，随着流量增大，高压区逐渐扩散到整个压水室，且蜗壳内壁的压力明显高于靠近叶轮区域。

图6 水泵在不同流量下静压分布

当流量增加到120 L/min后，将图6(c)与图6(b)比较可知，压力整体分布无太大差异，但在水泵出口扩散管靠近隔舌附近出现较大面积低压区。这是由于在水泵转速一定时，流量增加，液体从叶轮和压水室获得的能量减少，液体流经扩散管靠近隔舌附近时压力较小，这也是水泵扬程随着流量增加而减少的原因。

4.2 速度场分析

从图7可知，泵内流场的速度从入口到叶轮逐渐增大，离开叶轮时速度最大，可以明显观察到叶轮周围一圈的速度较大，而靠近蜗壳壁面的速度由于摩擦损失较小。液体离开叶轮后，绕着压水室流出水泵，受到阻力作用，速度有些损失。当水泵转速不变，增加流量时，在蜗壳的隔舌附近出现小面积的涡流，这是由于高压区与低压区之间的作用使得该区域流动紊乱。当流量达到140 L/min时，由于涡流的作用，有少部分液体本该顺着扩散管流出水泵，却从隔舌处流回压水室,在压水室也有两处明显的涡流现象。综上，该水泵在流量为90 L/min的设计工况，流速分布较为合理，没有出现明显的涡流、回流现象。

图7 水泵在不同流量下速度矢量分布

4.3 性能分析

4.3.1 扬程

扬程是水泵输送单位质量液体从入口处到出口处能量的增值，即水泵出口总水头H2与水泵入口总水头H1的代数差。

H=H2-H1

(1)

式中：H1为水泵入口截面处的总水头，又称吸入扬程；H2为水泵出口截面处的总水头，又称排出扬程。

(2)

(3)

式中：Pin、Pout为水泵入口、出口截面处液体的静压；P1、P2为水泵入口、出口截面处液体的总压；v1、v2为水泵入口、出口截面处液体的平均速度；Z1、Z2为水泵入口、出口截面中心到基准面的距离；ρ为流体密度；g为重力加速度。

水泵扬程的计算公式为：

(4)

该水泵为微型离心泵，可忽略水泵出入口之间的距离差值。由数值仿真结果可以得到，在转速为4 200 r/min、流量为90 L/min的工况下，P1=101 325 Pa，P2=137 525 Pa，H=3.698 m。

4.3.2 功率

水泵的功率分为轴功率和输出功率。

轴功率指原动机传输到泵轴上的功率，用Pa表示，轴功率包括机械摩擦功率ΔPm和水力功率Ph，而机械摩擦功率又包括圆盘摩擦损失功率ΔPy和轴承摩擦损失功率ΔPz。

Pa=Ph+ΔPm=Ph+ΔPy+ΔPz

(5)

水力功率Ph即作用在叶轮上的功率，可直接由数值仿真计算获得Ph=87.694 W。

圆盘摩擦损失功率ΔPy计算公式为：

(6)

式中：CD为摩擦阻力系数；R2为圆盘(叶轮)外半径；ω为圆盘旋转角速度；tB为圆盘外半径的总厚度。

计算可得ΔPy=2.1 W。

轴承摩擦损失功率ΔPz与轴承的结构形式、填料种类及加工工艺等有关，一般为轴功率的1%～3%，该水泵的设计工况为4 200 r/min，转速较高，取1%比较合适。由以上分析计算，可得轴功率Pa=90.69 W。

输出功率指传递给流经泵的液体的机械功率，即有效功率，用Pu表示，其计算公式为：

Pu=ρgQvH

(7)

其中，Qv为水体的流量。计算水泵在设计工况下的有效功率Pu=54.30 W。

4.3.3 效率

水泵效率即输出功率与轴功率之比：

(8)

计算水泵在设计工况下的效率η=59.87%。

4.3.4 基本性能曲线

按照以上方法，计算了该水泵在4 200 r/min下，不同流量大小下的特性参数，性能预测结果如表1所示，特性曲线如图8所示。

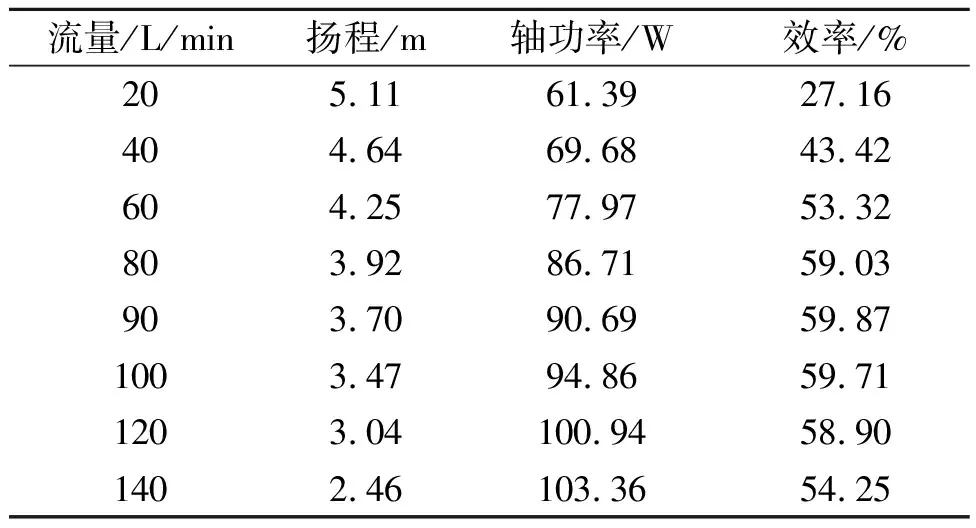
表1 水泵性能预测结果

图8 水泵在4 200 r/min下的特性曲线

从图8可知，该水泵转速为4 200 r/min时，扬程随着流量的增大而减小，轴功率随着流量的增大而增大。水泵的效率曲线呈现先增后减的趋势，根据拟合的趋势线，效率最高点出现在流量为104 L/min附近，计算可得效率最高点对应的效率为62%，扬程为3.35 m。

5 结论

(1)基于CFD方法能准确地反映离心式水泵的内部流场特性，通过水泵中间截面的压力分布云图和速度分布云图，能直观地表现水泵内部流场的压力和速度分布规律，观察到压力波动和涡流分布等不稳定流动情况，对水泵的性能预测和结构优化设计具有重要意义。

(2)所研究的模型在设计工况下的压力分布较为合理，没有逆压梯度较大的区域；流速分布也较为合理，没有出现大面积的涡流、回流现象。

(3)隔舌对泵内流动的影响较大，靠近隔舌附近有不同程度的涡流，并且随着流量的增大，涡流的面积逐渐增大。

(4)所研究的模型，在水泵转速为4 200 r/min时，其工作点应该选用在104 L/min处，对应的效率为62%，扬程为3.35 m。