速冻叉烧小笼包物流过程中中心温度变化研究
胡罗松,唐玉兰,吴春梅,白卫东,刘晓艳,白永亮
(1.广州酒家集团利口福食品有限公司,广东番禺511442;2.佛山科学技术学院食品科学与工程学院,广东佛山528000;3.仲恺农业工程学院,广东 广州510225)
0 引言
叉烧小笼包以可口、快捷、价廉而深受欢迎,但由于叉烧小笼包不能长时间贮藏,很难满足现代人的生活需求[1]。速冻叉烧小笼包的诞生为解决这一问题,提供了简洁高效的方法和途径,继承了叉烧小笼包的传统风味,食用时只需要复热,具有方便、快捷、性价比高等优点,是中国传统食品工业化的最佳切入点之一[2],然而在实际生产、冷藏、运输和销售过程中可能由于某些因素不可避免地存在温度波动,使速冻叉烧小笼包的中心温度发生变动,从而使小笼包常出现冻融循环现象,导致包点内水分的散失,严重影响其品质[3]。在此过程中发现包点产生冻纹、破裂、掉粉,透光性变差,水分不断散失,蛋白质含量降低,硬度和弹性呈下降趋势,黏性增大等现象[4-5]。综上,速冻包点的品质易受生产、冷藏、运输和销售过程中不利因素的影响,且影响极大[6]。在此,针对物流过程在不同条件下对速冻叉烧小笼包进行中心温度的测定,中心温度的变化会影响着速冻叉烧小笼包的品质,影响食用口感。不同的中心温度,其外观、口感不一。
1 材料与方法
1.1 材料与仪器
小麦粉、叉烧馅、燕子酵母等。
食品搅拌机、压面机、整形分割机、出馅机、阳政多功能包馅成型机、推车、气蒸柜、螺旋速冻机、包装机、温度记录器、冷链车、纸箱等。
1.2 试验方法
1.2.1 速冻叉烧小笼包的生产工艺
原料→和面→静置→压延→成型→醒发(37℃)→气蒸(390 s)→冷却(常温1 h)→速冻(-36℃,1 h)→包装(常温包装)→冷冻保藏(-18℃)→物流运输。
1.2.2 具体实施方法
在运输前将5根温度探针分别平行插入5个叉烧小笼包的中心位置,分别内包装,再将3根温度探针放入装有速冻叉烧小笼包的空隙位置,用来测定内包装环境温度,再各自内包装。将装有8根探针的叉烧小笼包分别装入5个纸箱里,随后第一时间随机装入小型冷冻货车进行物流运输,每隔1 h测一次中心温度,每到一个卸货点开一次门。以整个车箱(一批次)为研究整体,采用随机堆放的形式,考查物流运输对叉烧小笼包中心温度及箱子内包装环境的温度变化情况,旨在得出物流运输时间与叉烧小笼包到达门店的普适性温度范围之间的关系,指导速冻包点物流配送。
2 结果与分析
2.1 不同运输时间和开门次数下的中心温度
试验包括2个因素(A,B因素),每个因素设5个水平,并考虑因素之间的的交互作用,每个处理设置3个重复。
不同运输时间和开门次数下的中心温度见表1。

表1 不同运输时间和开门次数下的中心温度
2.2 物流过程中的中心温度对速冻叉烧小笼包品质的影响
不同速冻叉烧小笼包中心温度的交互作用对品质影响显著,中心温度越低,速冻叉烧小笼包的品质就越好,并且温度越低,对速冻叉烧小笼包的影响就越显著[7]。通过感官评价表明,在相同运输时间里,开门次数越多,速冻叉烧小笼包的中心温度越高,复蒸后的叉烧小笼包的口感较差[8]。在相同开门次数条件下,运输时间越长,速冻叉烧小笼包的中心温度越高,复蒸后的叉烧小笼包的口感较差[9]。
不同的速冻叉烧小笼包的中心温度间风味差异显著。中心温度为-15.04℃的速冻叉烧小笼包的风味优于-12.04℃和-10.82℃,差异不大。速冻叉烧小笼包中心温度对品质影响较大[10],且物流运输是温度波动较大阶段,所以研究不同运输时间和开门次数对速冻叉烧小笼包中心温度的影响十分重要[11]。
2.3 回归方程的建立
2.3.1 中心温度与运输时间之间的图像关系
中心温度与运输时间之间的图像关系见图1。
由图1可知,中心温度与运输时间呈正比,即中心温度随运输时间的增长而缓缓升高,并且在不同运输时间下,二者构成的图像斜率相近。

图1 中心温度与运输时间之间的图像关系
2.3.2 中心温度与运输时间之间的回归方程
在开门次数为1次时,中心温度Y与运输时间A之间的回归方程:Y=0.42A-15.46。
回归方程方差分析见表2。

表2 回归方程方差分析
由表2可知,在开门次数为1次时,中心温度与运输时间之间的回归方程Y=0.42A-15.46的效果极显著(p<0.01)。
在开门次数分别为2,3,4,5次时,中心温度与运输时间的回归方程如下:在开门次数为2次时,中心温度与运输时间之间的回归方程:Y=0.394A-14.828,效果显著(p<0.05);在开门次数为3次时,中心温度与运输时间之间的回归方程:Y=0.449A-13.983,效果极显著(p<0.01);在开门次数为4次时,中心温度与运输时间之间的回归方程:Y=0.445A-14.407,效果极显著(p<0.01);在开门次数为5次时,中心温度与运输时间之间的回归方程:Y=0.441A-13.665,效果极显著(p<0.01)。
2.3.3 中心温度与开门次数之间的图像关系
中心温度与开门次数之间的图像关系见图2。
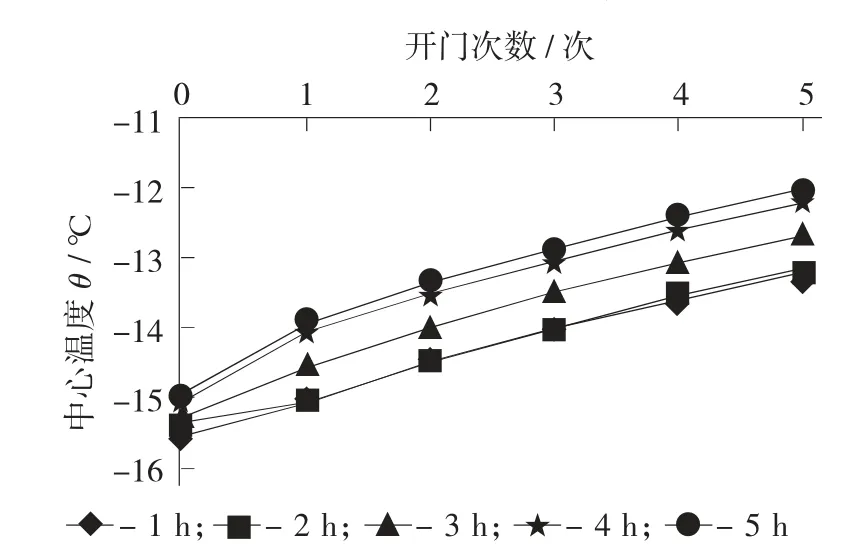
图2 中心温度与开门次数之间的图像关系
由图2可知,中心温度与运输时间呈正比,即中心温度随运输时间的增长而缓缓升高,并且在不同运输时间下,二者构成的图像斜率相近。
2.3.4 中心温度与开门次数之间的回归方程
在运输时间为1 h时,中心温度Y与开门次数B之间的回归方程:Y=0.478B-15.493。
回归方程方差分析见表3。

表3 回归方程方差分析
由表6可知,在开门次数为1次时,中心温度与开门次数之间的回归方程Y=0.478B-15.493,效果极显著(p<0.01)。
在运输时间分别为2,3,4,5 h时,中心温度与开门次数的回归方程如下:在运输时间为2 h时,中心温度与开门次数之间的回归方程:Y=0.456 0B-15.383,效果极显著(p<0.01);在运输时间为3 h时,中心温度与开门次数之间的回归方程:Y=0.510 9B-15.100,效果极显著(p<0.01);在运输时间为4 h时,中心温度与开门次数之间的回归方程:Y=0.543 7B-14.758,效果极显著(p<0.01);在运输时间为5 h时,中心温度与开门次数之间的回归方程:Y=0.558 9B-14.654,效果极显著(p<0.01)。
2.4 中心温度与运输时间、开门次数之间的关系
2.4.1 中心温度与运输时间、开门次数之间的图像关系
中心温度与运输时间、开门次数之间的图像关系见图3。

图3 中心温度与运输时间、开门次数之间的图像关系
由图3可知,中心温度随着运输时间、开门次数的增多而增大。
2.4.2 中心温度与运输时间、开门次数两因素之间的回归方程
回归方程为:Y=0.447A+0.398B-15.887。回归方程的显著性检验见表4。
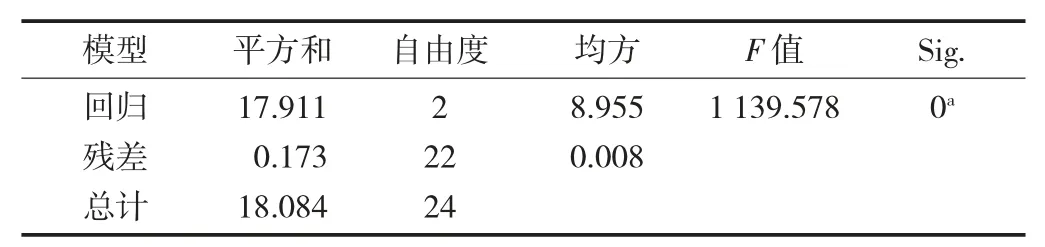
表4 回归方程方差分析
由表4可知,中心温度与运输时间、开门次数两因素之间的回归方程Y=0.447A+0.398B-15.887,效果极显著(p<0.01)。
3 结论
中心温度影响着速冻叉烧小笼包的品质,而运输时间、开门次数又对速冻叉烧小笼包的中心温度产生一定的影响。结果表明,运输时间各水平间,开门次数各水平间差异极显著(p<0.01)。在开门次数分别为1,2,3,4,5次时,建立的中心温度与运输时间之间的回归方程效果极显著(p<0.01)。在运输时间分别为1,2,3,4,5 h时,建立的中心温度与开门次数之间的回归方程效果极显著(p<0.01)。
在速冻包点冷链过程中,大多数采用感官评价和各指标检测法,没有明确的成熟加工工艺模式,并且国内将包点冷链的条件精确到回归方程的研究并不多见。而试验最终确定了中心温度与运输时间、开门次数的回归方程,从而为建立速冻叉烧小笼包冷链模型提供很好的理论依据,可以使速冻叉烧小笼包的冷链实现简单化和数字化,更好地保持原有的口感和品质,从而促进速冻包点产业的发展。因此,在速冻叉烧小笼包冷链物流过程中,生产商可以减少运输时间和开门次数,使消费者品尝到原汁原味的速度叉烧小笼包。

