基于蚁群遗传混合算法改进的连接查询研究*

张逸风，佟国香，刘 军，屈亚宁

(1.上海理工大学光电信息与计算机工程学院，上海 200093；2.山东山大华天软件有限公司，山东 济南 250000)

1 引言

产品生命周期管理PLM(Product Lifecycle Management)是支持产品信息创建、管理、分发和应用的一系列方案。PLM的核心技术之一是面向产品全生命周期的数据建模技术。目前PLM系统主要以文档管理为主，很难解决异构平台、跨单位、跨阶段和跨领域开发时的数据交互问题，因此，研发基于模型数据库的复杂产品全生命周期模型管理原型系统PLMM(Product Lifecycle Management of Model)成为工业4.0时代大趋势。而产品生命周期中的概念产生、产品设计、采购、生产制造、销售和服务等各个阶段的数据不仅数据量大，且相互关联错综复杂，目前主流的关系型数据库和数据仓库都可以作为PLM系统的数据服务支持平台。由于PLM系统的数据库结构的复杂度高，数据信息具有多样性，将数据抽象为模型后，模型之间的关联关系越来越复杂，耦合性越来越高等诸多因素降低了数据检索的效率，因此，选择合适的连接查询算法[1]尤为重要。

在传统联机事务处理OLTP(On-Line Transaction Processing)[2]的多表连接查询方式中，Hash Join[3]是近些年研究人员改进得最多的连接查询算法。因为其稳定性和有效性，自诞生以来研究人员就尝试从各方面对其进行改进。文献[4]介绍了一种散列合并连接算法HMJ(Hash-Merge Join)。它通过不可预测的、缓慢的或突发的网络流量处理来自远程数据源的数据项。算法综合运用了非阻塞连接算法X-Join和渐进式合并连接算法的优点，得到了更优的结果。文献[5]提出了一种新的基于NOWs(Network Of Workstations)的散列连接处理的负载共享算法,结合了分块方法和散列连接来管理当前环境中发生的动态变化，可以用于当前的单连接处理。文献[6]提出了一种基于列库的分布式环境中散列连接算法，面向数据的分布式计算模型的设计，引入分区聚合和启发式优化策略，实现了改进的哈希连接算法。

对于联机分析处理OLAP(On-Line Analytical Processing)[7]多表连接查询，由于数据量过于巨大，牵扯的关联表数量也大幅增加。Ripple Join[8]是主流的估算聚合值方法，轮流在每个表中随机采样，将采样的结果放入内存,对新放入内存的结果和所有现存的结果进行连接查询。这种方法要求采样的数据分布具有随机性，而现代数据库数据被聚类存放，因此不具有随机分布的特性。文献[9]对Ripple Join算法进行了并行性和采样方面的改进，该方法的局限性是，一旦内存无法再加载数据时，估计结果将不具有统计意义。Chris 等人[10]将sort-merge思想应用到Ripple Join算法中，对内存转出到外存的数据进行随机化处理，从而保证估计结果的统计意义，并在引擎DBO(Date Base Owner)上实现了该方法，提升了Ripple Join的部分效率。文献[11]介绍了Invisible Join，其思想是将表的相关列映射成位图，对维表主键属性相应的外键列建立一个事实表位图，根据所需要选择的位图和属性获得相应连接结果。文献[12]提出的Flash/Five Join是一种基于索引的多路等值的列式数据库连接算法，对连接列属性值进行排序，同时索引号随之变动，再将连接列属性值物化得到物化后的值，最后对索引号排序得到连接结果。Wander Join[13,14]是一种通过采样计算聚合值[15]的方法，设计了一个步行计划选择器代替随机采样，使得采样更有目的性，效率更高。通过合理应用Wander Join连接查询，用户将获得更高的聚合值返回效率，数据库系统可以支持更多元的运算。它的问题在于复杂性和适用性，以及对分组查询的查询速度不尽如人意。

本文将蚁群遗传混合算法[16]与Wander Join相结合，提出了优化连接顺序的连接查询算法。该算法通过一个连接选择器计算出连接表之间的代价，用于连接图建模时的顺序选择。执行连接图对应的连接计划后，使用剪枝策略对样本多余的节点进行剪枝操作，保留高选择性的节点，以减少节点的数量，避免重复搜索。最后将提出的混合连接算法在TPC-H(Transaction process Performance Council-H)数据集和TPC-DS(Transaction process Performance Council-DS)数据集[17,18]上分别进行了仿真验证。

2 Wander Join查询算法

Wander Join查询算法使采样过程更加集中，避免了盲目地从每个表中抽取样本进行连接操作，只从其中一个表中随机抽取一个元组，从该元组开始进行随机遍历，在随机遍历的每一步中，只考虑当前已采样元组及其相邻元组。与Ripple Join连接算法的“盲目搜索”相比，它是一种引导探索。

具体方法是将表之间的连接建模为连接图，然后在该连接图中执行随机遍历。由于可以用不同的顺序对相同的连接执行随机遍历，所以Wander Join查询算法设计了一个优化器来选择最优的遍历计划。由于每一条路径被选择的概率不相同，易导致采样不均匀，为了判断遍历计划的优劣，Wander Join引入HT(Horvitz-Thompson)估计量，用式(1)来估算样本总体的期望值[19]：

(1)

其中,n表示采样数目，XIi表示采样这个Ii得到的值，πIi表示出现采样的概率。而选择概率如式(2)所示：

(2)

其中,γ表示不同时刻，Rλ(1)表示第1个表里总记录的条数，dλ(i)(tp(i))表示从第i-1个表的某条记录连接到第i个表的边的数目。

在给定的时间内，最终估计量的方差与Var[X1]E[T]/T成正比，如式(3)所示：

(3)

其中,W表示游走总步数，Xi表示第i个随机游走的估计值，E[T]表示随机游走中查找的索引条目的平均值，T表示总运行时间，最终估计量的方差越小，越接近最优的游走方案。

3 改进的连接查询算法

本文引入蚁群遗传混合算法和裁剪搜索空间对Wander Join算法进行优化，算法流程如算法1和图1所示。

算法1改进的连接查询算法

Step1表节点建模：将N个表上的连接建模为连接图;

Step2连接顺序确定：引入蚁群遗传混合算法确定表连接顺序;

Step3执行选择计划：根据新的连接顺序执行计划;

Step4样本选择：采用剪枝策略缩小选择范围;

Step5完成连接查询。

Figure 1 Flow chart of improved algorithm 图1 改进算法流程图

3.1 表节点建模

数据库连接查询优化问题与传统的旅行商问题类似，目标是寻求一条代价最小的路径。本文提出的改进算法将需要进行连接查询的数据表建模成连接图，以最小代价提供连接查询路径，流程如下所示：

Step1初始化节点:每个表被建模为一个节点ci，i=1,2,…,N;

Step2节点连接:若2表之间存在连接条件，则2表之间形成一条边;

Step3形成连接图:整合节点和边形成连接图G(V,E)，其中V={ci|i=1,2,…,N},E为所有边组成的集合。

3.2 连接顺序确定

实体和群体的能力描述代表了它们执行任务的能力，是进行任务规划的根本依据。能力描述还将组织任务的可完成性判断转化成了描述任务逻辑的定理证明。另外，群体中成员的变更可能导致组织能力的变化，能力描述也能自然地将这种变化表现出来。

由于模拟生物或自然界的不确定算法易陷入局部最优，而基于启发式的确定算法存在收敛速度慢等问题，本文算法将蚁群算法与遗传算法相结合，将蚁群算法每次迭代的结果作为遗传算法的初始种群，用遗传算法产生的结果更新蚁群算法的信息素。同时，引入2种新的交叉算子，后期使用两元素优化(2-opt)算法，避免了算法过早陷入局部最优解，加快了算法的收敛速度，流程如下所示：

Step1生成初始种群。

(1)定义启发式信息素因子α，启发式期望值因子β，表节点连接代价d，信息素τ，启发式信息η，信息素强度q，交叉概率pe，变异概率pm，信息素挥发系数ρ等。

(2)禁忌表初始化为空。

(3)将蚂蚁释放在N个表节点上。

(4)状态及转移方向初始化，如式(4)所示：

(4)

(5)将表节点按照被遍历的顺序组成编码，把蚁群算法中所有蚂蚁遍历一次后的完整路径作为遗传算法的初始种群。

Step2执行选择。

按照1∶1的比例，采用轮盘赌方法和最优个体保存法对种群中的个体进行选择。第k个个体适应度被选择的概率pk和前k个个体被选择的累计概率qk如式(5)和式(6)所示：

(5)

(6)

其中，f(k)为适应度函数。

计算个体适应度在整个种群适应度中被选择概率和累计概率，最后通过0～1的随机数r与累计概率qk来决定被保留的个体。

适应度的计算采用目标函数和适应度函数，目标函数如式(7)所示：

(7)

其中，d(ci,cj)表示表节点ci到表节点cj的距离,Lk则代表蚂蚁k在一次迭代中走过的路径长度。

适应度函数选取目标函数f(Lk)的倒数，如式(8)所示：

(8)

可知，路径长度影响适应度，路径越长适应度越小。

Step3执行交叉。

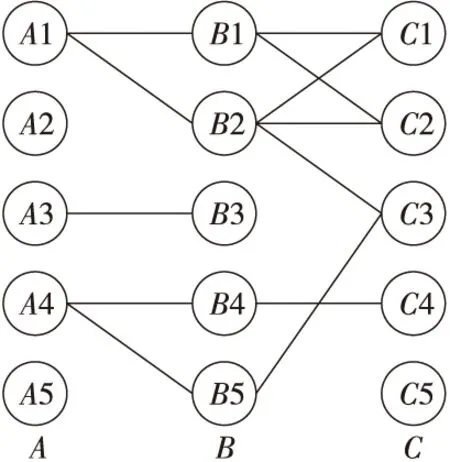
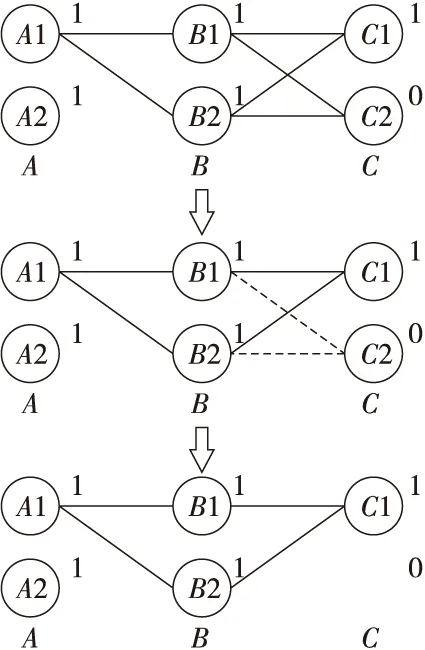
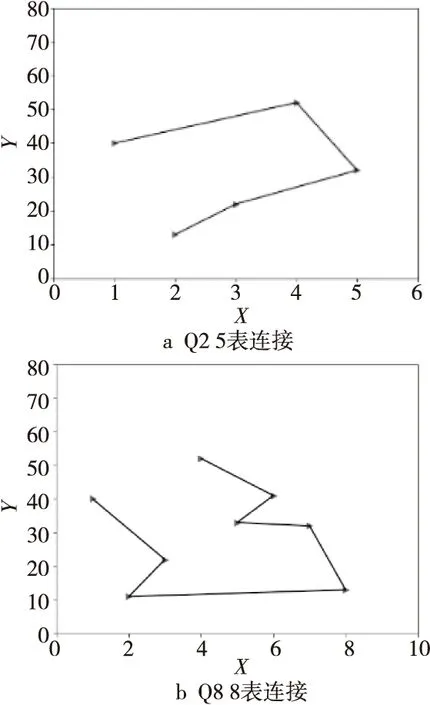
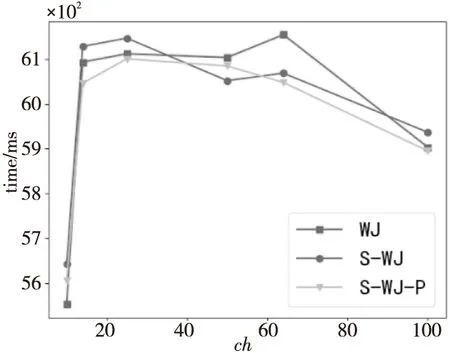
按照交叉概率进行交叉操作。从种群中随机确定个体a和个体b作为子代路径的父个体，随机确定一个交叉节点rc作为子代路径的起始节点。计算父个体a和b路径中节点rc与其下一个节点ca1和cb1之间的距离da1和db1，计算节点rc与ca2和cb2之间的距离da2和db2，如果da1+db2*r≤da2+db2*r,0

Step4执行变异。

对交叉后得到的结果采用对换变异，将随机选取的若干基因按照变异概率pm互换，初始概率选择较大的值，以便在更大范围内搜索，尽可能减小丢失最优解的概率。根据进化代数令变异概率pm递减，最终锁定最优解。

Step52元素优化(2-opt)。

从当前解中任意选择2条路径，拆成2个部分。在不构成环路的前提下，将第1部分的路径反接回另一条路径，比较产生的路径与原路径的长度，并保留路径相对较短的解。针对不同的路径重复进行2-opt，最终得到局部优化后的解。

Step6用式(9)更新信息素：

(9)

(10)

Step7若迭代次数大于最大循环次数或遗传算法的结果满足当前要求的最优解，输出最优连接路径结果P(x1,x2,…,xn)。

3.3 执行选择计划

根据3.2节中得到的新的查询连接顺序P(x1,x2,…,xn)，执行新的选择计划。

以图2为例，如果按照原始的查询顺序A→B→C，连接一次成功率为3/5，但是在优化连接顺序后，新的选择计划的查询顺序为C→B→A，则连接的一次成功率为4/5，达到了优化效果。

Figure 2 Data connection diagram图2 数据连接示意图

3.4 样本选择优化

删除未通过筛选的节点可以对高选择性查询样本进行优化，防止查询节点失败，使用更少的节点进行查询，以加快查询速度。优化过程如下所示：

Step1初始化权重。

在实践中，当发出过滤查询时，统一设置每个节点的权重。

Step2更新权重。

在进行抽样时，如果遇到一个节点未能通过筛选，将该节点的权值设置为0，并将此节点视为查询失败。通过将权值设置为0，保证不再对这个失败的节点采样。

Step3裁剪。

如图3所示，对于3张表A、B、C，可以看到2条可能的采样路径是A1→B1→C2和A1→B2→C2。如果连接选择了A1，B1，而节点C2没有通过筛选，则将C2的权重置为0，并裁剪。这样不仅消除了A1→B1→C2这条可能的路径，也消除了A1→B2→C2路径。删除没有通过筛选的节点，防止了任何路径对该节点进行再次采样。

Figure 3 Node clipping diagram图3 节点裁剪示意图

Step4输出裁剪后结果。如果再次执行同一查询计划，查询正确率将有所提升。

4 实验及结果讨论

本文实验环境为Python 3.6.5，实验数据集为TPC-H与TPC-DS。

实验参数设置：蚁群遗传混和算法种群规模M(k)=25,启发式信息素因子α=2,启发式期望值因子β=3,信息素挥发系数ρ=0.7,释放的信息素总量q=100,交叉概率pe=0.75,变异概率pm=0.05,遗传算法进化代数设为20，混合算法的总迭代次数达到100代时输出结果。

基于相对错误率、置信区间宽度、平均权重和执行时间对算法性能进行评估，并将蚁群遗传混合算法+剪枝策略+Wander Join改进的算法(本文算法，记作S-WJ-P)分别与蚁群遗传混合算法+Wander Join改进的算法(记作S-WJ)以及Wander Join算法(记作WJ)进行了对比实验。

相对错误率如式(11)所示：

(11)

其中,v表示方差，Ns表示抽样个数。

置信区间的左右值分别用L-int和R-int表示，半宽度(ε-width)公式为：

(12)

平均权重如式(13)所示：

(13)

其中,n为样本数量，wi为权重。

4.1 模拟多表连接顺序优化

把每个表节点映射为一个二维数组后，基于TPC-H数据集和本文算法获得的优化表连接路径如图4所示。

Figure 4 Minimum cost path of table join图4 表连接最小代价路径

为了验证在更大数量表连接时算法的可行性，模拟实验了20和50个表连接的情况，本文算法获得的优化表连接路径如图5所示。

Figure 5 Minimal cost path for a large number of table join图5 大量表连接最小代价路径

由图4和图5可见，表节点数量越多，路径选择就越多，本文算法容易找到相对最优解进行连接，从而减少连接的相对错误率。

4.2 实验结果分析

将置信度设置为95%，分别在样本数量为10 000和100 000的条件下，测试了3种算法在6个档次选择率情况下的相对错误率、执行时间、平均权重和置信区间宽度,结果如表1和表2所示。

对比表1和表2，在不同选择概率ch下，WJ的相对错误率波动较大，这是因为3.2节中提到的WJ的随机游走会导致路径不同，从而影响选择成功率，而S-WJ和S-WJ-P的相对错误率波动较小，说明改进的算法具有良好的鲁棒性。S-WJ-P和S-WJ的置信区间宽度与平均权重也均小于WJ的。以上实验结果表明，本文算法达到95%置信区间的收敛速度比WJ快，换言之，达到相同置信区间所需的样本数量比WJ的少。此外，由于剪枝策略的加入，裁剪了大量没有遍历的节点，因此在低选择率条件下获得了更好的优化效果，从而本文算法的估算结果更精确。

图6～图9给出了不同样本数量时的算法对比情况。从图6和图7给出的相对错误率的对比情况来看，在2种不同样本数量条件下，S-WJ-P在大部分选择率区间内的相对错误率均低于WJ和S-WJ的，只有在低选择率区间内S-WJ的相对错误率略低。3种算法的执行效率如图8和图9所示，S-WJ-P和S-WJ的执行时间均高于WJ的。这是因为引入的蚁群遗传混合算法和剪枝策略增加了算法的计算时间，但在样本数量大幅度增加后,由于剪枝策略有效减少了表节点数量，3种算法时间趋于一致，因此牺牲部分时间减少20%～70%的相对错误率是值得的。样本数量较少时的效率问题仍是后续改进算法的方向。

Table 1 Comparison of partial experimental results of 10 000 samples表1 10 000个样本部分实验结果对比

Table 2 Comparison of partial experimental results of 100 000 samples表2 100 000个样本部分实验结果对比

Figure 6 Comparison of relative error rate of 10 000 samples图6 10 000个样本相对错误率对比

Figure 7 Comparison of relative error rate of 100 000 samples图7 100 000个样本相对错误率对比

Figure 8 Execution time of 10 000 samples图8 10 000个样本执行时间

Figure 9 Execution time of 100 000 samples图9 100 000个样本执行时间

为了验证改进算法的普适性，基于TPC-DS数据集再次验证，从图10、图11与图6、图7中相对错误率的对比情况来看，在相同样本数量条件下，S-WJ-P在大部分选择率区间内的相对错误率均低于WJ和S-WJ的。实验结果表明，改进算法具有更高的正确率和更好的鲁棒性。

Figure 10 Comparison of relative error rates of 10 000 samples on TPC-DS图10 TPC-DS上10 000个样本相对错误率对比图

Figure 11 Comparison of relative error rates of 100 000 samples on TPC-DS图11 TPC-DS上100 000个样本相对错误率对比

5 结束语

本文提出了一种基于Wander Join改进的数据库连接查询算法，利用蚁群遗传混合算法优化表连接的路径选择，结合Wander Join算法，使连接查询得到部分优化。按照新的连接顺序进行连接后，引入剪枝策略，减少连接节点数量。实验表明，算法在控制相对错误率和控制样本数量方面取得了较好的效果。选择率为10%左右时，改进算法表现最佳，相对错误率只有Wander Join算法的1/5。改进算法在数据库更新操作时会破环剪枝的效果，加上蚁群算法的处理时间，导致执行时间增加。今后的研究可以尝试连接算法的并行化，或与其它启发式算法结合，引入强化学习算法全面提升其性能。