光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体的非线性能谱特性*

张爱霞 姜艳芳 薛具奎

(西北师范大学物理与电子工程学院, 兰州 730070)

(2021 年4 月14 日收到; 2021 年5 月26 日收到修改稿)

1 引 言

光晶格中的超冷原子物理在理论上和实验上受到了人们的重点关注. 因为光晶格不存在任何杂质和缺陷, 且光晶格中的超冷原子系统可以在广泛的参数范围内调节, 为量子计算和强关联多体系统的量子模拟创造了理想的条件, 例如量子纠缠以及拓扑相变的研究等[1-4]. 此外在光晶格系统中还发现了许多有趣的动力学现象, 例如Bloch 振荡[5-10]、Landau-Zener 隧穿[11-14]、局域化[15,16]、超流相到莫特绝缘相的相变[17,18]等. 更重要的是, 原子间相互作用的非线性还可以极大地改变布洛赫带的结构, 使能带在第一布里渊区的边界处呈现出燕尾形状的环状结构(loop 结构)[19-23]. 这主要是由光晶格势和非线性相互作用之间的竞争导致的, 当相互作用较大时, 能带中会出现loop 结构. 可以通过观察Bloch 振荡的破坏以及非线性Landau-Zener隧穿现象的发生, 间接地证明能带中loop 结构的存在[9]. 因此光晶格周期势为研究玻色-爱因斯坦凝聚体的相关物理特性提供了很好的平台[24-32].

近年来, 利用光与原子间的相互作用, NIST小组在87Rb 玻色-爱因斯坦凝聚体中实现了一维人工自旋轨道耦合, 为超冷原子气体的研究开辟了新的思路[33]. 随后, 山西大学和中国科学技术大学分别在40K 费米气体和87Rb 冷原子中实现了二维自旋轨道耦合[34,35]. 最近, 中国科学技术大学与北京大学等合作, 通过将普通光晶格和拉曼光晶格相对转角的方法, 在国际上首次实现了三维人工自旋轨道耦合[36], 且构造出有且只有一对外尔点的理想外尔半金属拓扑能带结构, 超越了传统凝聚态物理的外尔型拓扑物理的量子模拟, 为研究拓扑输运性质以及量子模拟新奇现象打开了新的方向. 此外, 实验上也成功实现了运动光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体, 证明了自旋轨道耦合会破坏该系统的伽利略对称性[37]. 光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体的实现激发了人们对其基态特性的研究[38-40], 发现系统中存在4 种基态相, 即具有单一波矢的非极化和极化Bloch 相以及由两个具有相反波矢Bloch 波叠加的条纹相. 同时初步研究发现, 对于静止的光晶格, 一定参数范围内的最低Bloch 带还可以产生平带, 且系统能量最小值可以出现在第一布里渊区内的任何位置[41].而移动的光晶格则会使Bloch 谱变得复杂, 这主要是由自旋轨道耦合系统中缺乏伽利略不变性导致的, 因此自旋轨道耦合成为导致系统能谱特性复杂化的又一重要因素. 事实上在自由空间, 自旋轨道耦合和原子间相互作用的耦合也会导致系统能带中出现loop 结构, 并且伴随着Landau-Zener 隧穿和自旋交换动力学[42]. 可以设想, 自旋轨道耦合与光晶格的耦合必然会使系统的能谱特性更加复杂化. 但是目前对光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体的非线性能谱特性的研究还很初步.

本文主要研究了光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体的非线性能谱结构和流密度. 先简单地介绍了系统模型, 然后通过两模近似和变分法得到了系统的能量, 接着展示了不同系统参数对布里渊区边界附近能带结构的影响, 讨论了系统能带在布里渊区边界出现loop 结构的临界情况, 最后研究了不同自旋态流密度的变化规律.

2 模型和变分法

2.1 理论模型

考虑一维浅光晶格中赝自旋1/2 的自旋轨道耦合玻色-爱因斯坦凝聚体, 自旋轨道耦合是由Rashba 和Dresselhaus 型自旋轨道耦合等权叠加形成的. 在平均场近似下, 该系统可以通过如下无量纲平均场能量泛函描述[37-40]:

研究发现, 光晶格对第一布里渊区附近自旋轨道耦合玻色-爱因斯坦凝聚体的基态能带结构有显著的影响[38-40]. 而且对于浅晶格或者中间深度的光晶格, 两模近似不仅可以给出G-P 方程在最低能带第一布里渊区边界处的精确解, 还可以给出在布里渊区附近的近似解[5,6,11,19], 因此为了深入地研究布里渊区边界附近最低能带的变化特性, 使用如下形式的两模近似试探波函数:

式中, 假定自旋对称相互作用, 即g11=g22=g和δ=0. 为了获得系统的能带结构, 使用变分法, 对(5)式中的变分参数s和θ变分. 即令∂E/∂s=0 ,∂E/∂θ=0, 可得变分方程如下:

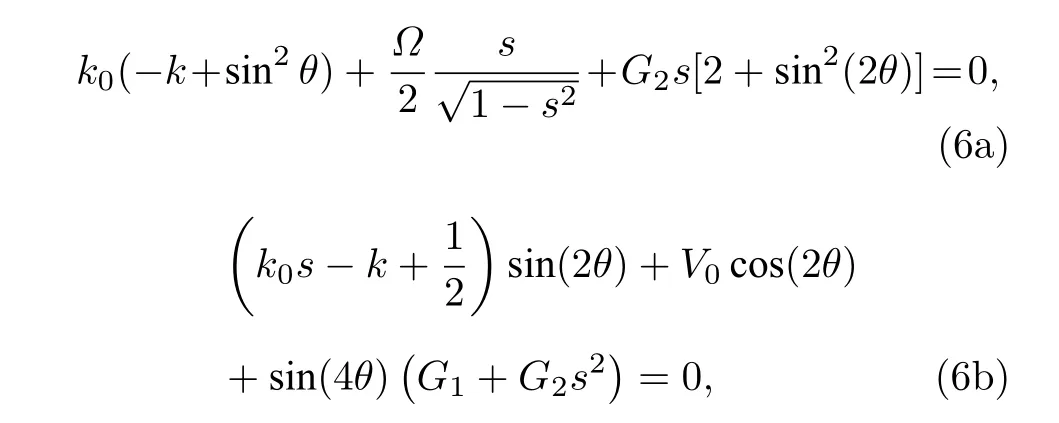
其中G1=(g+g12)/4 ,G2=(g −g12)/4 . 通过数值求解变分方程中的θ和s, 并代入系统能量(5)式中, 便可以研究不 同参数下的能谱结构图. 可以清楚地看到, 系统的能量是由拉曼耦合强度Ω, 自旋轨道耦合强度k0, 光晶格强度V0和原子间相互作用共同决定. 下面展示不同系统参数对能谱结构的影响.

2.2 非线性能谱结构

图1 是在不同系统参数下的最低能带. 可以看出, 在最低能带的布里渊区的边界处, 即k=0.5 处出现了特殊的loop 结构. 而且在每一行中(请看第2 行—第4 行中V0=0.2 情况), 随着拉曼耦合Ω的增大, loop 宽度先变小, 然后在布里渊区边界处出现尖点, 最后loop 消失. 每一列中, 随着自旋轨道耦合强度k0的增大, 能带先在边界附近出现尖点, 继续增大k0, 布里渊区的边界处出现了loop 结构, 最后loop 的宽度变大的同时能带结构变得更加复杂(如每一列中V0=0.2 情况). 在每一副子图中不同颜色对应着不同的光晶格强度, 对于较小的光晶格强度V0, 能带结构在布里渊区的边界处先出现了较大的loop 结构, 继续增大V0, 能带在边界处出现尖点, 最后loop 消失(如k0=0.3,Ω=1.5 情况). 总之, 我们发现拉曼耦合和光晶格强度抑制了最低能带在边界处loop 结构的出现, 自旋轨道耦合促进了loop 结构的产生, 使loop 结构变得更加复杂. 能带结构中不同能量最小值处(图1 中用小球表示)的凝聚体处于不同的基态相, 为了进一步研究能量最小值处凝聚体所处的基态相, 图2 给出了不同拉曼耦合下的极化图. 可以看出, 当自旋轨道耦合强度k0较小时(k0=0.2 ), 能量最小值处的凝聚体处于非极化的Bloch 相 (图2 中的所有黑球).随着k0的增大, 当s ̸=0 时凝聚体处于极化Bloch 相,相反, 当s=0 时凝聚体处于非极化Bloch 相.

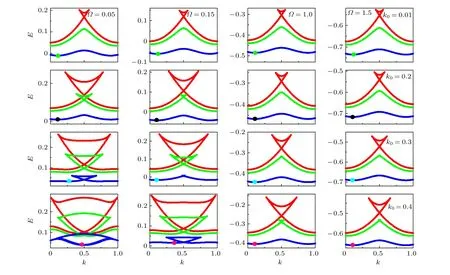
图1 不同系统参数下的非线性能谱结构. 每副子图中不同的颜色代表不同的光晶格强度, V0 =0.05 (红色), 0.2 (绿色),0.4(蓝色). 能量最小值处用不同颜色的小球表示. 其他参数:g =0.2, g12 =0.1Fig. 1. Nonlinear energy band structure for different system parameter. Different colored curves in every subplots correspond to different optical lattice strength, V0 =0.05 (red), 0.2 (green), 0.4 (blue). The energy minima is indicated by different colored ball. The other parameters are g =0.2 and g12 =0.1 .

图2 不同拉曼耦合 Ω 下的极化图. 其他参数:g =0.2,g12 =0.1,V0 =0.4Fig. 2. Spin polarization s as a function of Raman coupling Ω for different k0 . The other parameters are g =0.2 ,g12 =0.1and V0 =0.4 .

能带布里渊区边界处loop 结构的出现, 还与原子间相互作用有关. 为了进一步研究原子间相互作用对能带结构的影响, 图3 中绘制了不同种间原子间相互作用g12下的能带. 可以发现: 最低能带中不仅在布里渊区的边界处(k=0.5 )出现loop 结构, 在远离边界的两端也有loop 的存在(图中在k=0,1附近). 同时在高能带的布里渊区边界处也出现了loop 结构, 而且随着g12的增大, 不同位置的loop 结构宽度都变大, 能带中还会出现高低能带loop 交叉等更加复杂的现象. 由此可知, 原子间相互作用的非线性效应会使能带中loop 结构更加复杂.

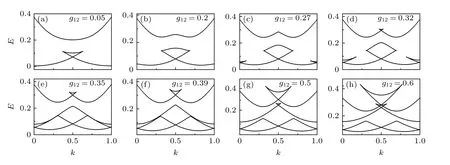
图3 不同种间原子间相互作用 g12 下的非线性能谱结构. 其他参数: Ω =0.1 , k0 =0.2 , V0 =0.1 ,g =0.1Fig. 3. Nonlinear energy band structure for different interspecies interaction g12 . The other parameters are Ω =1.0 , k0 =0.4 ,g =0.2and g12 =0.1 .

2.3 能带出现loop 结构的临界条件

当最低能带在布里渊区边界处出现尖点时, 便是达到了出现loop 的临界条件. 为了直观地观测不同参数对最低能带布里渊区边界处出现loop 结构的影响, 绘制了不同自旋轨道耦合k0下, loop 结构出现的临界Ω图(图4). 从图4 可以发现, 在k0-Ω平面, 较强的光晶格使loop 的区域向大自旋轨道耦合区域扩展. 当k0一定时, 弱拉曼耦合Ω有利于loop 结构的出现, 随着k0的增大, 较强的拉曼耦合Ω才会使能带中不出现loop. 此外, 增大种间原子间相互作用g12(图4(b)和图4(c)), 当k0较小时, 光晶格强度V0对能带在布里渊区边界处出现loop 结构的临界Ω的影响减弱. 随着k0的增大,较强的光晶格强度则需要更大的拉曼耦合值才能使最低能带的边界处不出现loop 结构.

图4 g =0.2 时最低能带出现loop 的临界 Ω , (b) 中不同形状的符号表示相应光晶格强度下(9)式给出的理论值Fig. 4. Critical condition for appearing the loop structure in the lowest energy band at g =0.2 . The different symbols in panel (b)represent the theoretical values given by Eq. (9) under the corresponding optical lattice strength.

为了进一步理解自旋轨道耦合、拉曼耦合、光晶格和原子间相互作用对形成loop 的竞争机理,针对g=g12的情况进行了理论分析. loop 结构最先在布里渊区边界出现, 在变分方程(6a)和(6b)中令k=1/2且G2=0 , 即g=g12, 消去s可得

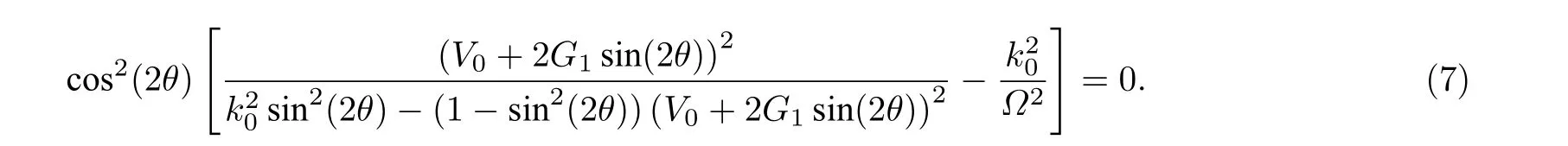
要想在布里渊区边界出现loop 结构, 则方程(7)中的θ应有两个解, 即满足 cos(2θ)=0 和

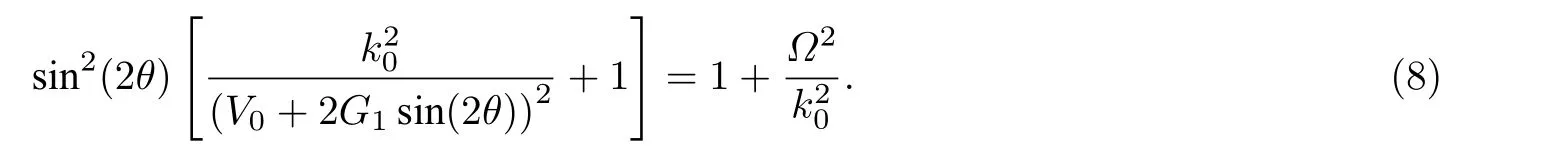
当sin(2θ)有根且满足−1 ≤sin(2θ)≤1 时, 则有1+(Ω/k0)2≤/(V0−2G1)2+1,即

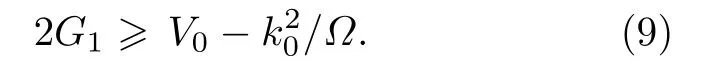
(9)式给出了g=g12时系统在布里渊区边界处出现loop 结构的临界条件. 图4(b)中进一步展示了理论和数值结果的对比, 可以看出, 数值与理论符合得很好. (9)式充分揭示了自旋轨道耦合、拉曼耦合、光晶格和原子间相互作用对形成loop 的竞争机理, 即自旋轨道耦合k0的增大(拉曼耦合Ω的减小)等效于改变了系统的光晶格势能, 亦即降低了在布里渊区边界处出现loop 所需的非线性原子间相互作用能阈值. 当不存在自旋轨道耦合, 即k0=0时, (9)式退化为普通光晶格系统中出现loop 的临界条件, 即相互作用能大于光晶格势能.总之, 自旋轨道耦合和原子间相互作用促进了系统最低能带loop 结构的出现, 拉曼耦合和光晶格抑制了loop 结构的产生.

3 凝聚体流密度

在布里渊区的边界附近, 非线性能谱结构的变化与凝聚体的流密度密切相关, 不同自旋态的流密度定义如下:

将两模近似波函数(4)代入(10)式可得不同自旋态的流密度

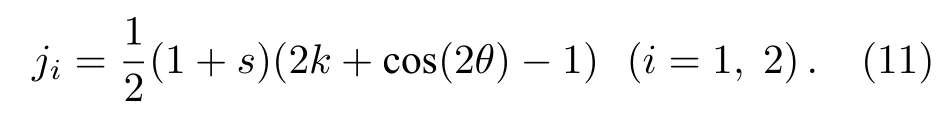
数值求解变分方程组(6a)和(6b)中的s和θ,代入(11)式可得到在布里渊区边界附近非线性Bloch 波的流密度. 图5 是与能带图图1 第二列对应的不同自旋态的流密度图. 从图5 可以发现, 当自旋轨道耦合强度k0较小时, 不同自旋态的流密度基本重合. 若能带在布里渊区边界处无loop 结构,则在k=0.5 处的凝聚体流密度为零, 即ji=0 , 凝聚体将维持Bloch 振荡, 同时将伴随着弱的自旋交换(例如k0=0.01,V0=0.2 ). 随着k0的增大, 虽然布里渊区边界处的凝聚体流密度ji仍然为0, 但是流密度呈现出一定的不对称性(例如k0=0.1,V0=0.2), 且在动量空间中不同自旋态流密度的分布发生分离, 凝聚体在进行Bloch 振荡的同时, 自旋交换加强. 继续增大k0, 在布里渊区边界附近相同凝聚体动量所对应的流密度ji出现多值, 相应的能量值出现多根, 所以能带结构在布里渊区边界处出现了loop 结构(例如k0=0.2,V0=0.2 ), 破坏了系统的Bloch 振荡, 使原子在不同Bloch 带之间发生了非线性Landau-Zener 隧穿, 由于两自旋态的流密度在动量空间的分布明显分离, 因此自旋交换也加强. 另外, 从图5 还发现, 光晶格强度的增大不仅减小了能带结构布里渊区边界处的loop宽度,同时使不同自旋态的流密度在动量空间中重合, 减弱了流密度的不对称性和自旋交换.

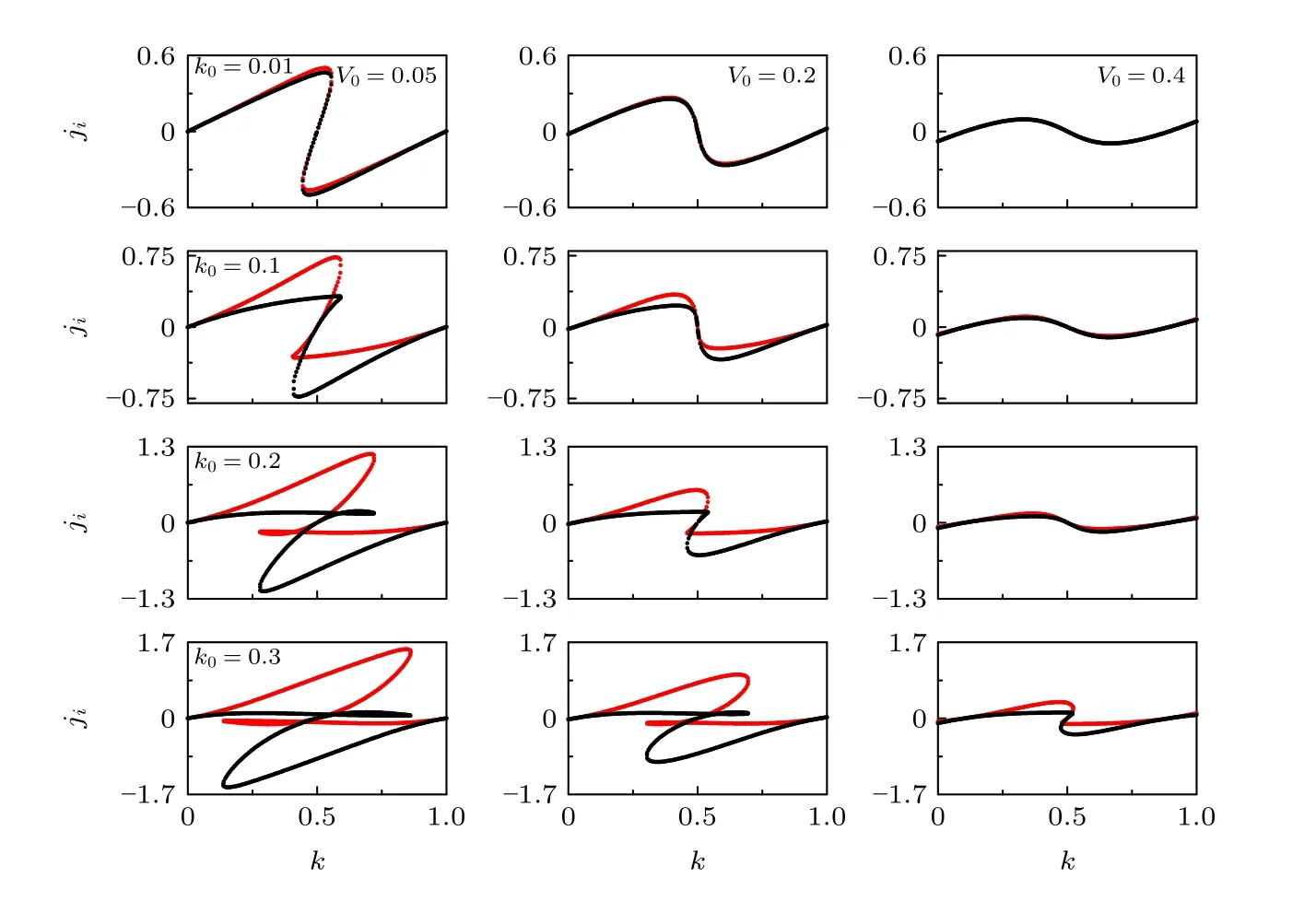
图5 不同自旋轨道耦合 k0 和光晶格强度 V0 下的凝聚体流密度. 其他参数: Ω =0.15 , g =0.2 , g12 =0.1 . 图中红色和黑色的线表示不同自旋态的凝聚体流密度Fig. 5. Current density for different spin-orbit coupling k0 and optical lattice strength V0 . The other parameters are Ω =0.15 ,g =0.2and g12 =0.1 . The red and black lines represent the current density of different spin states.

图6 进一步研究了自旋轨道耦合与拉曼耦合对不同自旋态流密度的耦合影响. 从图6 可以直观地发现, 随着Ω的增大, 能带结构中loop 宽度减小的同时, 凝聚体流密度的不对称性减弱. 当自旋轨道耦合强度k0较小时(图6 第一、二行k0=0.1 ),不同自旋态的流密度基本重合且自旋交换较小, 但是随着k0的增大(图8 第三、四行k0=0.2 ), 不同自旋态的流密度呈现出明显的不对称性. 而Ω的增大会强烈地减弱这种不对称性, 使不同自旋态的流密度的变化规律与无自旋轨道耦合的情况相似. 同时还发现, 在动量空间loop 宽度所对应的凝聚体动量, 正好与凝聚体流密度中出现多值所对应的动量区间一致(图中用粉色垂线表示), 所以可以通过直接地观测凝聚体流密度出现多值的区域来研究loop 结构的大小.

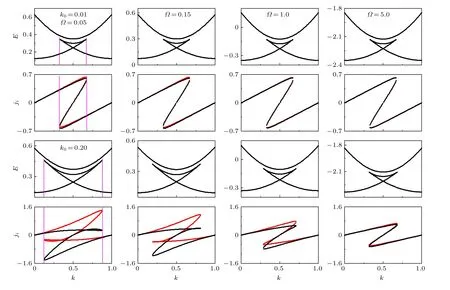
图6 不同拉曼耦合 Ω 下的能带和相应的凝聚体流密度. 其他参数: V0 =0.05 , g =0.2 , g12 =0.1 . 图中红色和黑色的线表示不同自旋态的流密度Fig. 6. Energy band and current density for different Raman coupling Ω . The other parameters are V0 =0.05 , g =0.2 and g12 =0.1. The red and black lines represent the current density of different spin states.

4 结 论

本文研究了光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体的非线性能谱结构和流密度, 揭示了自旋轨道耦合、拉曼耦合、光晶格以及原子间相互作用对系统能带特性的影响, 发现系统能谱结构在布里渊区的边界处会出现loop 结构. 拉曼耦合和光晶格强度会抑制loop 结构的出现, 而自旋轨道耦合和原子间相互作用促进loop 结构的产生. 自旋轨道耦合会使能带结构变得更加复杂, 而原子间相互作用的非线性还会使高能带的布里渊区边界处出现loop 结构. 非线性能谱结构的变化与凝聚体的流密度有密切的关系, 当能谱结构在布里渊区边界处不存在loop 结构时, 边界处的不同自旋态流密度为零. 出现loop 结构时, 边界处的凝聚体流密度出现多值. 此外, 自旋轨道耦合还会使布里渊区边界附近的流密度呈现出强烈的不对称性, 使不同自旋态流密度在动量空间的分布分离, 而光晶格强度和拉曼耦合强度则会减弱这种不对称性, 使不同自旋态流密度重合. 布里渊区边界处loop 结构的出现破坏了系统的Bloch 振荡, 使系统发生Landau-Zener 隧穿, 而不同自旋态流密度在动量空间分布的分离意味着自旋交换动力学的出现.