楔形铜基底-单层石墨烯覆层表面液滴自驱动研究*

张福建 陈悦 高翔 刘珍 张忠强3)‡

1) (江苏大学智能柔性机械电子研究院, 镇江 212013)

2) (江苏科技大学船舶与海洋工程学院, 镇江 212003)

3) (常州大学, 江苏省光伏科学与工程协同创新中心, 常州 213164)

(2021 年5 月13 日收到; 2021 年5 月28 日收到修改稿)

1 引 言

液滴定向自驱动在自然界中广泛存在, 例如沙漠甲虫利用背部的凸起结构收集液滴[1], 猪笼草吻部特殊的沟槽结构实现水的单向运输[2]等. 明确液滴自驱动的特性和机理对于实现水收集[3,4]、固体表面自清洁、微流控芯片[5]等应用具有重要价值.目前, 液滴驱动主要分为液滴自驱动和外场作用下的驱动. 外场作用下的驱动具有需要外场输入、控制复杂等特点[6-8], 在宏观尺度存在能量消耗, 在微纳尺度难以精确添加外场. 而液滴自驱动则是依靠基底的形貌梯度[9,10]、表面润湿梯度[11]、刚度梯度[12]等来驱动液滴, 由基底自身的润湿梯度决定液滴自驱动的方向, 无需外场输入, 实现了简单高效的液滴驱动. 例如, 梯度密度排列的柱状结构实现水滴从柱稀疏端向密集端移动[13], 锥形曲率结构实现水滴从圆锥尖端向尾端的自主运输[14,15]. 然而, 基底表面缺陷产生的液滴移动接触线钉扎通常会影响液滴的运动[16-18]. 基于猪笼草吻部和U 型岛阵列的非对称结构可以利用钉扎现象防止液体回流[19,20], 从而实现连续液体的定向铺展, 但是无法驱动单个液滴, 而基于莱顿弗罗斯特效应克服液滴接触线钉扎以驱动液滴的方法又表现出控制困难的特点[21,22], 且莱顿弗罗斯特效应需要高温, 无法适用于生物微流控芯片、水收集等领域. 因此,在常温状态下克服钉扎阻力实现液滴快速自驱动显得尤为重要.

单层石墨烯作为一种二维热点材料, 近年来已受到广泛关注. 已有研究表明, 基于单层石墨烯的润湿透明性和低流-固界面摩擦[23,24], 单层石墨烯覆层在缺陷基底上可有效降低液滴进入和脱离缺陷时的钉扎阻力[25]. 此外, 水滴在单层石墨烯上的快速扩散已被报道[26], 进一步地, 液滴在单层石墨烯覆层的柱状和凹槽铜基底上实现单向快速自驱动[27,28],表明单层石墨烯在液滴自驱动领域的巨大潜力.

本文提出了一种楔形铜基底-单层石墨烯覆层结构(monolayer graphene-covered wedge-shaped copper substrate, GWCS), 用以实现液滴的单向超快速自驱动. 采用分子动力学方法研究了液滴在GWCS 上的自驱动行为, 探索了基底表面润湿梯度和Young-Laplace 压力梯度驱动液滴的机理,明确了液滴最大位移与基底润湿性、基底角度和液滴表面张力之间的关系. 进一步分析了楔形基底宽度非连续线性增加对液滴自驱动的作用机制, 并确定了基底角度和液滴尺寸对液滴自驱动的影响规律. 最后, 研究了楔形基底两侧凹槽深度对液滴自驱动机理和液滴输运效率的影响机制. 研究结果对实现液滴自驱动的单层石墨烯覆层的功能织构表面设计具有理论指导意义.

2 模型和方法

分子动力学模型由带有楔形结构的铜基底、单层石墨烯和纳米水液滴组成, 铜原子尺度σCu-Cu=0.2314 nm[29], 碳原子尺度σC-C= 0.340 nm[30],单个水分子直径约为0.385 nm, 模拟盒子大小为60 nm × 33 nm × 16 nm. 铜基底楔形结构的楔角为α, 长度为34 nm, 楔形铜基底左侧延伸出长约4 nm、宽约1.3 nm 的长方体结构, 用于在放置液滴时起到支撑作用, 为了使楔形铜基底两侧的石墨烯不被吸附进楔形基底两侧的凹槽, 将凹槽深度设置为2 nm，如图1 所示. 将单层石墨烯覆盖在带有楔形结构的铜基底上0.2857 nm (C-Cu 原子间的平衡距离)处. 将铜基底楔角底部的底板、楔角左侧的长方体结构和x方向上的单层石墨烯两端各1 nm 设为刚性, 弛豫0.5 ns, 使得单层石墨烯吸附在铜基底上. 水纳米液滴的直径为d, 水分子采用TIP4P-EW模型[31], 将水纳米液滴弛豫0.5 ns, 使其达到能量最小化的平衡状态, 然后将液滴的质心放置在铜基底楔角结构最左侧的正上方, 液滴底部距离单层石墨烯0.328 nm (C-O 原子间的平衡距离)[27].

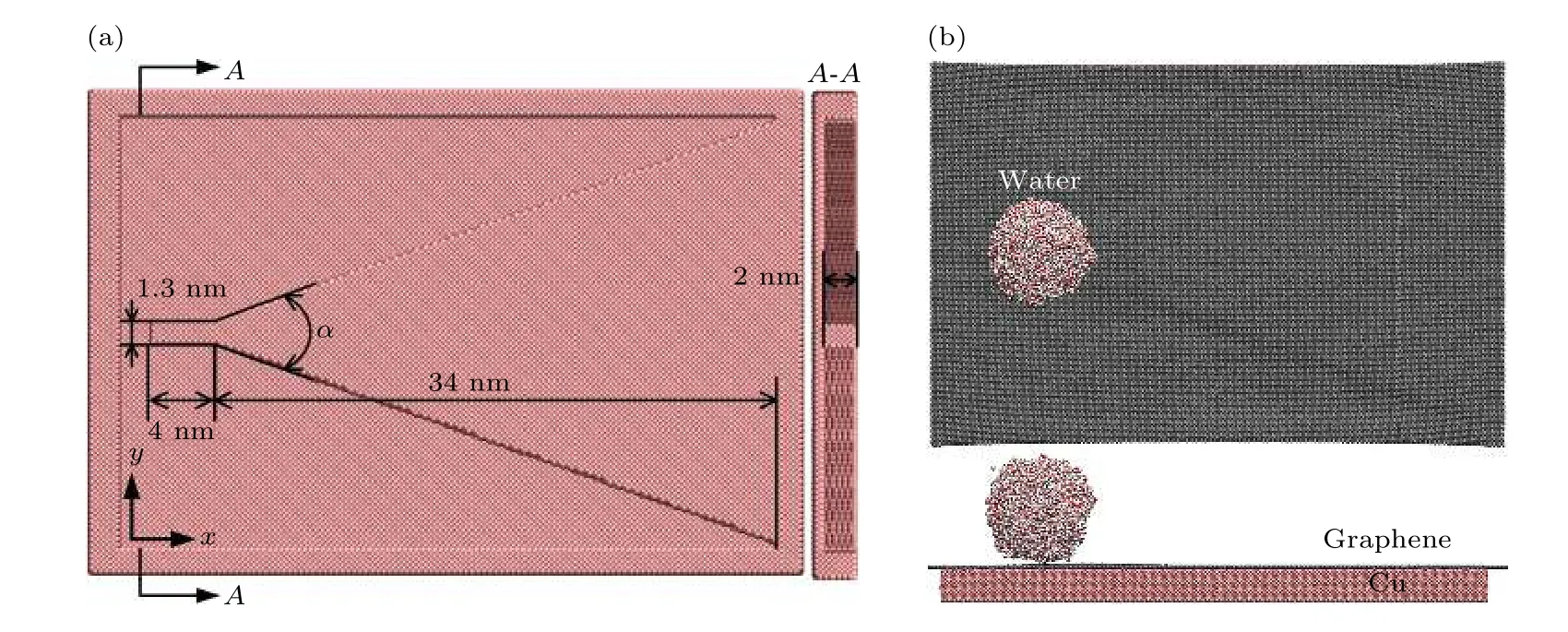
图1 水纳米液滴在GWCS 上定向运输模型 (a)楔形铜基底模型的俯视图和A-A 方向剖视图, 楔形铜基底包括中间的楔形基底、楔形基底两侧的凹槽和凹槽底部底板; (b)水纳米液滴在GWCS 上的俯视图和正视图. 粉色是铜基底, 黑色是单层石墨烯, 红白相间的球是水纳米液滴Fig. 1. Uni-directional self-driving model of a water nanodroplet on GWCS: (a) Top view and A-A sectional view of wedge-shaped copper substrate, the wedge-shaped copper substrate includes wedge-shaped substrate in the middle, grooves on both sides of the wedge-shaped substrate and a copper plate at the bottom of the grooves; (b) top view and front view of water nanodroplet on GWCS. The pink is Cu substrate, the black is monolayer graphene, and the red and white sphere is water nanodroplet.

模拟采用开源软件LAMMPS, 使用正则系宗将模拟温度控制在298 K, 时间步长为LAMMPS模拟的最小时间步长1 fs. 碳原子之间的相互作用由第二代REBO 势函数来描述, 铜原子之间的相互作用采用EAM 来描述. 水分子、铜、石墨烯之间的相互作用由Lennard-Jones (LJ)势函数来描述, 不同原子间相互作用势函数参数由Lorentz-Berthelot混合准则得到, 势函数参数如表1 所列[29,30,32]. LJ相互作用和库仑相互作用的截断半径均设置为12 Å,长程静电相互作用采用Particle-Particle Particle-Mesh 算法计算. 氢原子和其他原子之间的平衡距离和势阱深度设置为0[31].

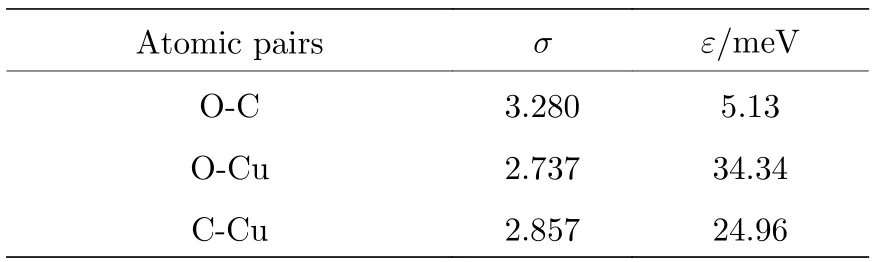
表1 不同原子之间的LJ 势能参数Table 1. Parameters of LJ potential between different atoms.

3 结果和讨论

首先研究了直径为8 nm 的水纳米液滴(8960 个水分子)在楔角α= 40°的GWCS 上的自驱动行为. 液滴的速度、位移随时间的变化关系如图2 所示. 在无任何外场的作用下, 液滴沿着楔角宽度增加的方向运动, 液滴的运动速度先随着时间的增加而增大, 在t= 0.358 ns 时, 速度达到最大值56.2 m/s (202.32 km/h). 而后液滴速度快速减小, 并在t≈ 0.68 ns 时减小到0, 此时液滴的最大位移为21.1 nm, 液滴质心所在位置的楔形基底宽度为16.2 nm. 最后, 当液滴位移达到最大值时, 液滴完全处于楔形基底上面, 由于液滴在前进方向上的弹性形变, 液滴发生原地振荡, 位移略有回落.以上结果表明GWCS 可以实现液滴从楔形基底尖端向宽端的定向自驱动.

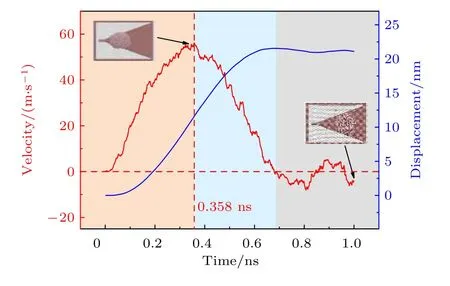
图2 液滴自驱动的速度、位移与时间的关系, 液滴直径为8 nm, 楔形基底角度为40°, 插图分别为液滴在0.35 和1.00 ns 时的运动状态, 单层石墨烯模型设置为线条结构且未显示铜基底底板Fig. 2. Velocity and displacement of the water droplet selfdriving on GWCS. The diameter of the water nanodroplet is 8 nm, and the wedge angle of GWCS is 40°, the illustrations show the motion of the droplet at 0.35 and 1.00 ns, respectively. The monolayer graphene model is set to linear structure and the bottom plate of copper substrate does not show.

为了揭示水纳米液滴在GWCS 上的自驱动行为, 计算了水纳米液滴在前进方向上的受力F和液滴与GWCS 之间的相互作用能随时间的变化关系, 如图3 所示. 液滴在前进方向上的受力F决定了液滴的速度变化, 力F从正数开始, 先增大后减小, 当F减小到0 时, 液滴速度达到最大(图3(a)).然后, 力F继续减小, 导致液滴速度快速下降. 最后, 随着液滴速度的减小, 力F逐渐增加至0 附近,液滴速度最终减小到0. 为了进一步探索液滴的受力来源, 计算了液滴与GWCS 之间的相互作用能随时间的变化关系, 如图3(b)所示. 在液滴从楔形基底的尖端向宽端运动的过程中, 液滴与铜基底之间的相互作用能Ew-Cu逐渐减小, 表明液滴可以透过单层石墨烯与铜基底发生相互作用, 印证了单层石墨烯的润湿透明性. 然而, 液滴与铜基底之间的相互作用能Ew-Cu的变化量远小于液滴与单层石墨烯之间的相互作用能变化量, 表明单层石墨烯在液滴自驱动过程中占主导作用. 同时, 随着液滴位移的增大, 液滴所在位置的楔形基底宽度逐渐增大, 导致液滴与GWCS 之间的相互作用能Ew-GCu逐渐减小, 减小的流-固界面相互作用能为液滴的自驱动提供能量. 当液滴达到最大位移后, 液滴完全处于楔形基底上, 液滴与基底之间的相互作用能基本不再变化. 此外, 由于液体的表面张力, 液滴表面积的变化会改变液滴的势能. 在液滴自驱动过程中, 液滴的势能呈现出增加的趋势, 当液滴达到最大位移后, 液滴原地振荡, 势能在一定范围内波动, 趋势上不再增加. 考虑到液滴总是往能量降低的方向运动, 而在液滴达到最大位移之前, 流-固界面相互作用能的减小和液滴势能的增加表明流-固界面相互作用能和液滴的势能之间存在竞争关系,即减小的流-固界面能有部分转化为液滴的势能,并非完全作用于液滴驱动.

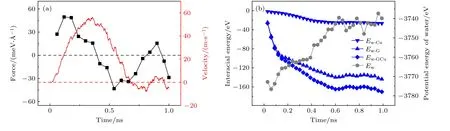
图3 (a) 液滴前进方向所受的合力F 和速度随时间的变化关系; (b) 液滴的势能、液滴与GWCS 之间的相互作用能随时间的变化关系. Ew-Cu, Ew-G 和Ew-GCu 分别为液滴与铜基底、石墨烯、GWCS 之间的相互作用能, Ew 为液滴的势能Fig. 3. (a) Resultant force F and velocity of the droplet in +x direction as a function of time; (b) potential energy of water droplet and the interfacial interaction energy between water droplet and GWCS versus time. Ew-Cu is the interaction energy between water droplet and copper substrate, Ew-G is the interaction energy between water droplet and graphene, Ew-GCu is the interaction energy between water droplet and GWCS, Ew is the droplet potential energy.

从理论上分析, 液滴自驱动过程中受到的驱动力可以分为两个阶段: 表面润湿梯度驱动和Young-Laplace 压力差驱动. 当液滴在GWCS 上的接触面包括楔形基底和沟槽正上方的单层石墨烯时(图4(a)), 水纳米液滴在单层石墨烯、单层石墨烯覆层的铜基底上的接触角分别为57°和29°, 所以单层石墨烯的亲水性小于单层石墨烯覆层的铜基底, 表面润湿梯度占主导作用, 将液滴从沟槽正上方的单层石墨烯表面推到单层石墨烯覆层的楔形基底上, 推力F0垂直于楔形基底的边线, 液滴从楔形基底的尖端向宽端运动. 此时, 液滴前进方向上受到的驱动力Fdri可以表示为

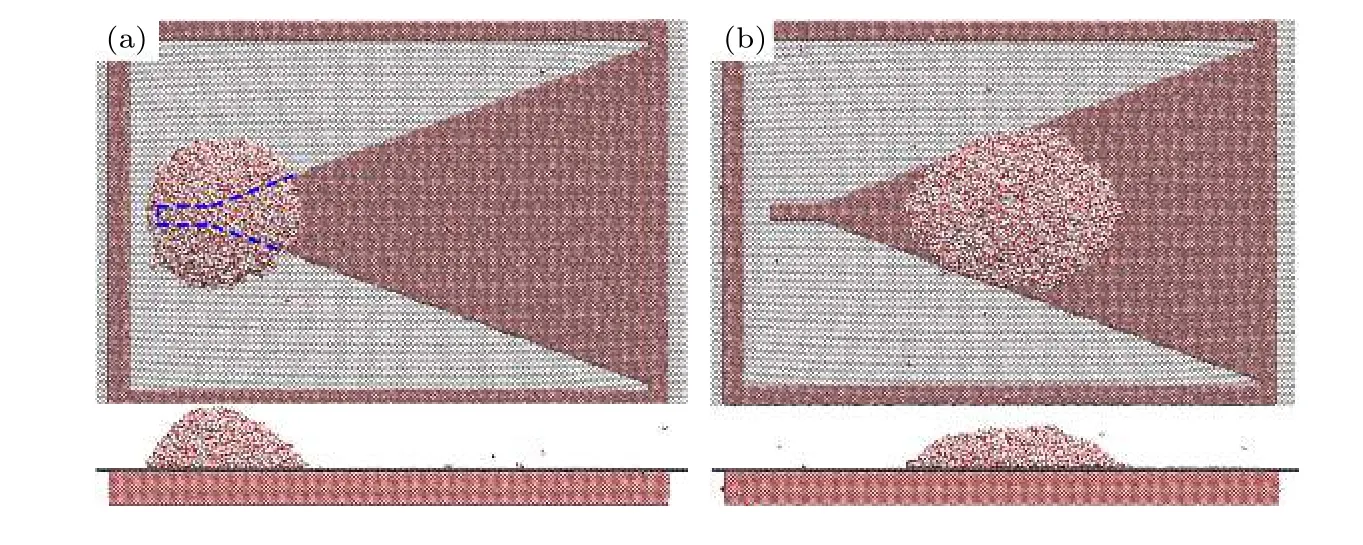
图4 液滴自驱动过程中在GWCS 上的两种接触状态的俯视图和正视图(未显示铜基底底板, 且俯视图中的单层石墨烯为线条结构) (a) 液滴在GWCS 上的接触面包括楔形基底和沟槽正上方的单层石墨烯; (b) 液滴完全处于楔形基底上Fig. 4. Top and front view of two contact states of the water droplet on GWCS in the self-driving process (the bottom plate of copper substrate is not shown, and the monolayer graphene in the top view is linear structure): (a) Contact area of the droplet on the substrate includes the wedge-shaped substrate and the graphene right above the groove; (b) droplet is completely on the wedgeshaped substrate.

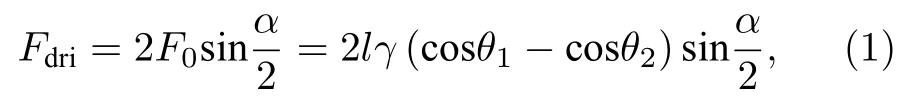
式中,l为液滴与楔形基底边线的接触线长度,θ1和θ2分别是液滴在单层石墨烯覆层的铜基底和单层石墨烯上的接触角,γ为水的表面张力, 如图5(a)所示. 液滴与楔形基底边线的接触线长度l可以进一步表示为

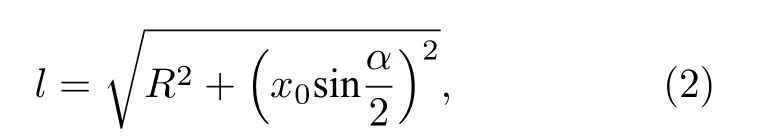
式中R为液滴在GWCS 上接触线的轮廓半径,x0为液滴所在位置到楔形基底虚拟尖端的距离.

随着液滴位移的增加, 当液滴开始完全处于楔形基底上时, 液滴在基底上的润湿形态如图4(b)所示, 液滴内部的Young-Laplace 压力差驱动占主导作用. 液滴在楔形基底上运动时的Young-Laplace驱动力Fdri可以表示为[5]

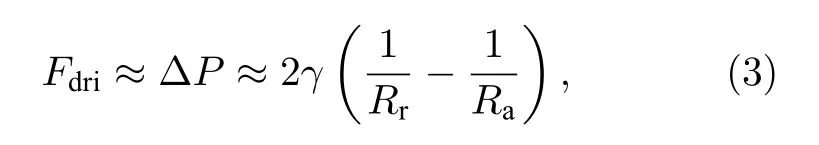
式中, ΔP为液滴内部的Young-Laplace 压力差,Ra和Rr分别为液滴在楔形基底上的前、后接触线的轮廓半径.

当液滴完全处于楔形基底上, 且液滴完成自驱动时, 液滴在基底上的位置如图5(b)所示, 液滴在基底上的最大位移xmax可以表示为

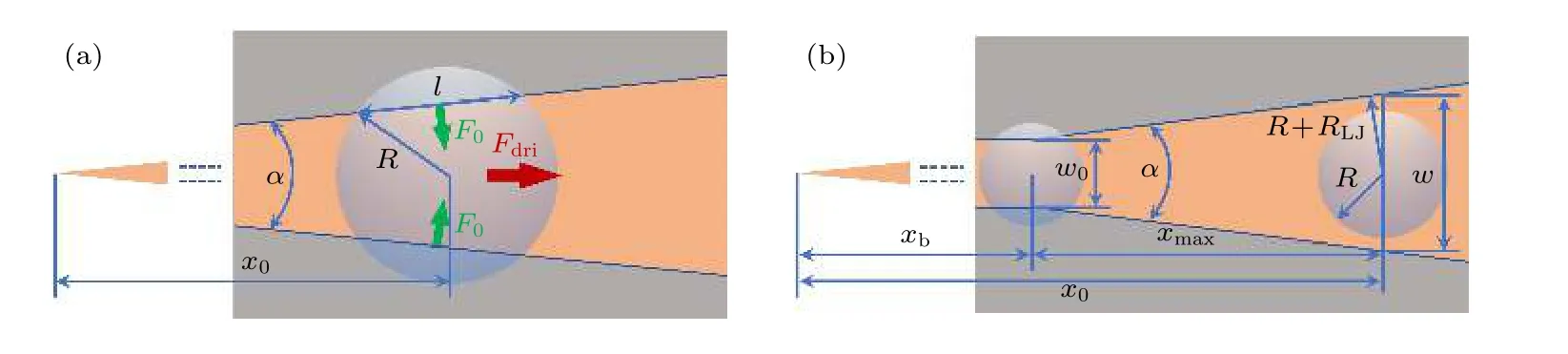
图5 (a) 液滴在楔形基底上的驱动力示意图; (b) 液滴达到最大位移时所在基底上的位置Fig. 5. (a) Driving force diagram of the droplet on GWCS; (b) position of the droplet on the substrate when the droplet reaches the maximum displacement.

根据(1)式—(4)式可以得出在本模型中影响液滴自驱动行为的参数有楔角和液滴直径. 为研究铜基底楔角对液滴驱动的影响, 楔角α选取40°,30°, 24°和20°, 分别计算了8 nm 液滴在不同楔角的GWCS 上的自驱动速度、位移随时间的变化关系, 结果如图6 所示. 可以看出, 在加速阶段, 液滴在GWCS 上的加速度随着楔角α的增大而增大,且液滴达到最大速度所用的时间随着楔角角度的增大而减小(图6(a)). 这是因为表面润湿梯度的方向垂直于楔形基底的边线, 楔形基底角度越大, 表面润湿梯度产生的液滴推动力F0在液滴前进方向上的分力越大, 即液滴在较大角度的楔形基底上拥有更大的驱动力Fdri. 然而, 液滴的最大位移随着基底楔角的减小而增大, 但楔角越大, 液滴越快达到最大位移(图6(b)). 同时, 随着楔角的减小, 液滴的速度产生了较大的波动, 这是因为液滴在小角度楔形基底上受到的驱动力更小, 导致自驱动行为更易受到原子热振荡的影响. 此外, 楔形铜基底的宽度是每隔一段距离k增加两层铜原子(图7), 而不是连续的线性增加, 使得GWCS 的润湿梯度并非连续, 造成液滴在单层石墨烯覆层的楔形铜基底上的前进方向驱动力会随着楔形基底宽度的增加而产生跨越式改变. 受液滴尺寸的影响, 间隔距离k越大, 液滴前进方向上受到的驱动力波动越大,这是造成液滴在小角度楔形基底上速度具有较大波动的另一重要原因. 对于本文, 当楔形基底的楔角α为20°时, 间隔距离k为 1.1 nm, 相对于液滴直径8 nm 来说已经是一个不可忽略的重要因素,表现在数据上则是由于液滴前进方向驱动力不稳定导致液滴在20°楔角的基底上的速度相比于40°楔角的基底具有较大的速度波动, 在液滴自驱动的末端尤为明显(图6(a)).

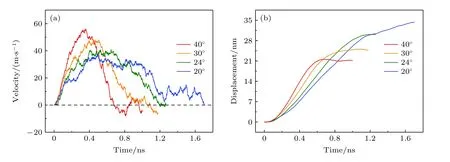
图6 楔形基底角度对液滴自驱动的影响 (a) 液滴运动速度; (b) 液滴的位移随时间的变化关系Fig. 6. Influence of the wedge angle of GWCS on the droplet self-driving behaviors: (a) Velocity and (b) displacement of the droplet on GWCS with different wedge angles versus time.

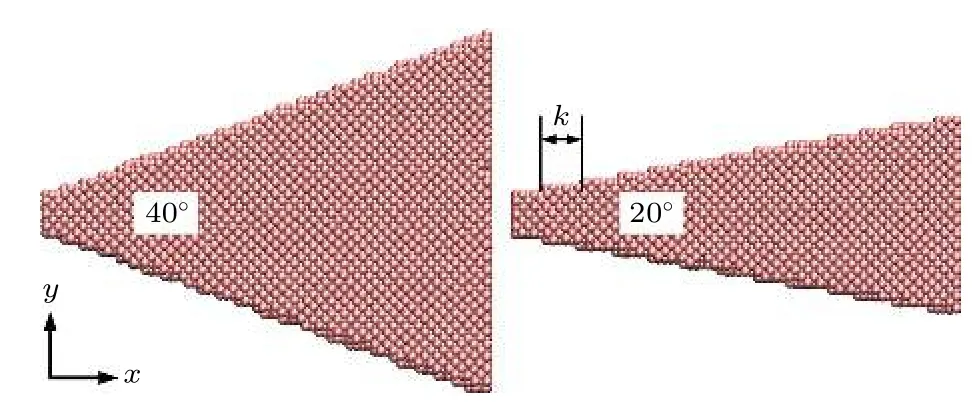
图7 不同角度的楔形铜基底, x 方向每间隔距离k, y 方向增加两层铜原子宽度Fig. 7. For the GWCS with different wedge angles, when the interval distance is k in x direction, the width of the wedge-shaped copper substrate increases two layers of copper atoms in y direction.

为了进一步明确楔形基底角度对液滴自驱动的影响, 绘制了液滴自驱动的最终位移与所在位置楔形基底宽度的理论值与模拟值对比图, 如图8 所示. 理论值分别由(4)式和(5)式计算得到. 受间隔距离k的影响, 液滴需要跨过间隔距离k才能达到下一个润湿梯度, 导致液滴在小角度楔形基底上的最终位移和所在位置基底宽度的模拟值小于理论值. 随着楔形基底角度的增大, 间隔距离k逐渐减小, 模拟值与理论值的差距逐渐缩小, 当楔形基底角度α为40°时, 位移的理论值和模拟值相近.同时, 考虑到液滴运动速度较大, 在无润湿梯度的基底上仍能减速运动一段距离, 导致液滴在40°楔形基底上的最终位移和所在位置的基底宽度的模拟值略大于理论值.

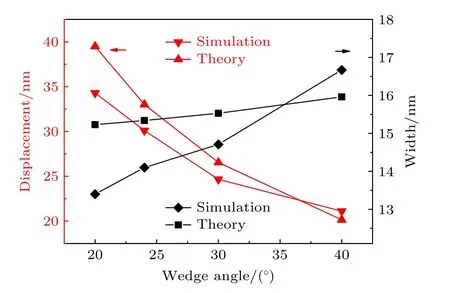
图8 液滴在不同楔角GWCS 上的自驱动最终位移、所在位置楔形基底宽度的模拟值与理论值对比Fig. 8. Comparison of the simulation and theoretical results of the final self-driving displacement and the width of wedge-shaped substrate with different wedge angles respectively.

此外, 研究了液滴尺寸对液滴在GWCS 上自驱动行为的影响, 计算了不同直径的纳米水液滴(6, 7, 8 和9 nm, 水分子数分别为3780, 6000, 8960和12750)在楔角α为40°的GWCS 上的速度、位移随时间的变化关系, 如图9 所示. 结果表明, 较小的液滴在加速阶段拥有较大的加速度, 其中6 nm 液滴的最大速度可以达到73.8 nm/s, 但是较大液滴的运动速度更为平稳(图9(a)). 然而,6 和7 nm 直径的液滴尺寸较小, 易受到原子热振荡的影响, 且两者体积差别小于7, 8 和9 nm 直径液滴之间的差距, 导致6 nm 直径液滴的速度与7 nm 液滴的速度和最终位移相近. 随着液滴直径增加到8 和9 nm, 液滴的最终位移表现出随液滴直径的增加而增加的明显趋势(图9(b)). 为了研究高速运动的液滴在无织构基底(驱动力消失后液滴所在位置的基底)上的减速运动对液滴最终位移的影响, 绘制了液滴最终位移的模拟值与理论值((4)式)随液滴直径的变化关系和模拟值与理论值的差值相对于液滴直径的比率图, 如图9(c)所示.直径在6—9 nm 范围内的液滴, 最终位移的模拟值与理论值的差值随着液滴直径的增大而减小, 表明6 nm 直径的液滴在无织构基底上减速运动的距离要大于7 nm 液滴, 这也是造成6 nm 液滴和7 nm 液滴最终位移相近的原因之一. 此外, 液滴最终位移的模拟值xsim与理论值xmax的差值相对于液滴直径d的比率 ratio=(xsim−xmax)/d随液滴直径的增大而减小, 表明高速运动的小液滴在无织构基底上更易产生滑动, 而大液滴能够抑制这种滑动使得液滴最终位移的模拟值与理论值更加契合.

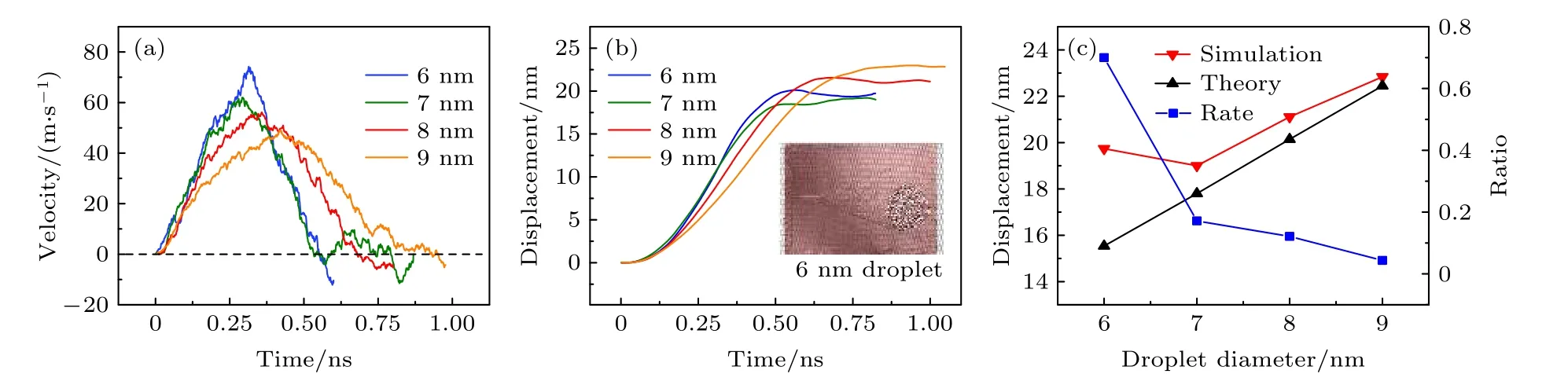
图9 液滴直径在6-9 nm 范围内时液滴尺寸对液滴自驱动的影响 (a) 液滴的速度和(b)液滴的位移随时间的变化关系, 插图为6 nm 液滴的最终位置; (c) 液滴最大位移的模拟值与理论值随液滴直径的变化关系和模拟值与理论值的差值相对于液滴直径的比率Fig. 9. Influence of water droplet size on the droplet self-driving behaviors when the droplet diameter in the range of 6-9 nm:(a) Velocity and (b) displacement versus time, the illustration is the final position of the 6 nm droplet; (c) simulated and theoretical values of the droplet displacement versus droplet diameter, and the ratio of the difference between the simulated value and the theoretical value to the droplet diameter.

最后, 讨论楔形铜结构两侧的凹槽深度对液滴自驱动行为的影响. 分别计算了凹槽深度为0.542 nm(3 层铜原子)和0.904 nm(5 层铜原子)情况下的8 nm 直径液滴自驱动效果. 液滴的速度、位移随时间的变化关系如图10 所示. 结果表明, 在凹槽深度为0.542 和0.904 nm 情况下, 液滴整体速度小于凹槽为2 nm 时的液滴速度(图10(a)), 且在凹槽深度为0.542 和0.904 nm 情况下液滴的最大位移约为8 nm, 远小于凹槽深度为2 nm 时21.1 nm的最大位移(图10(b)). 这是因为, 当凹槽深度为0.504 和0.904 nm 时, 单层石墨烯被吸附进凹槽内(图10(c)), 造成基底的表面润湿梯度消失, 不会产生凹槽深度为2 nm 时凹槽正上方的单层石墨烯将液滴推到楔形基底上的行为. 此外, 当单层石墨烯被吸附进凹槽时, 液滴两侧会铺展到凹槽内, 液滴仅依靠楔形基底左侧的结构梯度和楔形基底左端的长方体结构两侧与石墨烯之间的吸附间隙产生的微小润湿梯度驱动液滴. 因此, 凹槽深度决定了单层石墨烯是否会被吸附进凹槽内, 进而决定了液滴的驱动力来源和自驱动效率. 在单层石墨烯不被吸附进凹槽时, 液滴拥有最大的自驱动速度和最远的输运距离.

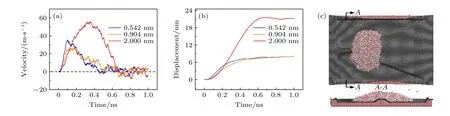
图10 楔形铜结构两侧凹槽深度对液滴自驱动的影响 (a) 液滴的速度和(b)液滴的位移随时间的变化关系; (c) 8 nm 直径液滴在凹槽深度为0.904 nm 的GWCS 上最终运动状态Fig. 10. Influence of groove depth on both sides of wedge-shaped copper structure on the droplet self-driving: (a) Velocity and (b) displacement of droplet versus time; (c) final motion state of 8 nm diameter droplet on GWCS with 0.904 nm groove depth.

4 结 论

本文采用分子动力学方法研究了液滴在GWCS上的自驱动行为, 计算了楔形基底角度和液滴尺寸对液滴自驱动的影响. 结果表明, 液滴受基底表面润湿梯度和Young-Laplace 压力梯度驱动, 实现了从楔形基底尖端向宽端的超快速定向自驱动, 最大速度可达73.8 m/s, 并给出了液滴在楔形基底上的最大位移与基底润湿性、基底角度和液滴表面张力之间的理论关系; 能量变化规律表明, 液滴的势能与流-固界面相互作用能存在竞争关系, 即液滴与基底之间的相互作用能有部分转化为液滴的势能,并非完全作用于液滴驱动; 在微纳尺度下, 楔形基底宽度为非连续线性增加, 宽度增加的轴向间隔距离随基底角度的减小而增大, 导致小角度基底的润湿梯度连续性较差, 小角度基底上的液滴速度波动相对较大, 且液滴在小角度基底上的位移小于理论值; 在大角度基底上, 小液滴更易获得较大的驱动速度, 同时由于液滴与基底之间接触面积较小, 小液滴在无润湿梯度阶段会产生较长距离的减速运动, 导致其实际位移要大于理论值; 当楔形铜结构两侧凹槽深度较大, 无法将单层石墨烯吸附进凹槽时, 液滴拥有最大的自驱动速度和最远的输运距离.