二维耦合谐振子的非对易能谱

苟立丹

(长春理工大学物理学院, 长春 130022)

(2021 年1 月14 日收到; 2021 年6 月9 日收到修改稿)

1 引 言

非对易空间的概念很早就被提出了[1], 但最初并没有引起人们的重视. 后来由于弦理论的发展[2],非对易研究重新受到了人们的关注. 研究人员开始探索一些领域中的非对易效应, 例如量子引力[3,4]、凝聚态物理[5]等. 很多问题被纳入到了非对易空间中进行研究[6-8], 例如谐振子[9]、氢原子[10]、朗道能级[9,11]等. 通常研究非对易空间量子系统的方法是将非对易算符通过映射的方法投影到对易空间, 使得算符满足标准的海森伯代数, 从而解决非对易问题. 2008 年范洪义等[12]把不变本征算符方法(invariant eigen-operator method, IEO)引入到非对易范畴, 用于求解非对易空间谐振子哈密顿量的能谱. 该方法是在海森伯思想和薛定谔算符的基础上提出的一种求解量子系统能谱的方法[13,14], 已经在物理学的很多领域有着广泛的应用, 如固体物理[15,16]、介观物理[17,18]、二次型哈密顿量[19]等. 研究表明IEO 方法对于处理非对易空间谐振子的能谱问题是比较有效的. 目前已有学者用IEO 方法研究过非对易相空间中任意维谐振子[20]、双模耦合谐振子[21]、三模耦合谐振子能谱[22].

耦合谐振子模型是量子理论、固体物理、原子分子物理等领域中的基础模型, 对于研究多体问题和关联系统的相互作用具有重要的理论意义和实际价值. 例如: 晶体中原子排列成有序的结构, 原子与原子之间的相互作用可以用耦合谐振子模型进行模拟, 耦合参数可以描述相互作用强度. 此外,还有很多的物理问题都可以简化到耦合谐振子模型, 因此研究非对易空间中的耦合谐振子能谱特性是很有意义的[23-25]. 文献[26]利用坐标变换将非对易问题变为对易问题, 然后用通常的量子力学方法求解. 文献[27]介绍了变形量子化方法, 即通过引入时间演化函数和魏格纳函数进行求解.

目前的研究结果普遍存在两方面的问题, 一是对于非对易空间, 只考虑了坐标和坐标不对易的情形, 而忽视了动量和动量的不对易, 以及两者同时存在不对易的情形[26]; 二是耦合谐振子模型的哈密顿量只含有某一类耦合项, 并没有讨论同时包含多种耦合项的哈密量的本征问题[21,22,26,27].

在非对易的理论框架下出现了很多新的问题,由于坐标算符之间的不对易和动量算符之间的不对易, 所以求解耦合谐振子的能谱并非易事. 而IEO方法源于海森伯方程, 无须涉及系统的具体量子态, 只关注能级间隙, 避免了哈密顿量的对角化,可以比较容易地解决一些问题. 因此本文尝试用IEO 方法研究坐标和动量同时存在不对易的非对易相空间中二维耦合谐振子的量子特性. 用该方法可以较方便地得出同时包含坐标坐标耦合、动量动量耦合及坐标动量交叉耦合项的哈密顿量的能级差, 进而得到体系的非对易能谱. 然后详细分析了非对易参数和耦合参数对于非对易能级的具体影响, 得到了一些有意义的结果.

2 不变本征算符方法

量子力学中海森伯运动方程为(采用自然单位制 ℏ=1 )

引入不变本征算符O, 使其满足方程

由(3)式可知λ=Eb−Ea, 因此,λ就是系统的能级差 ΔE.

3 二维耦合谐振子的非对易能谱

在一般的对易空间中, 坐标算符xi和动量算符pi满足海森伯代数关系:

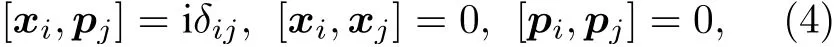
其中i,j=1,2 .在非对易相空间中, 坐标算符Xi和动量算符Pi满足以下关系:

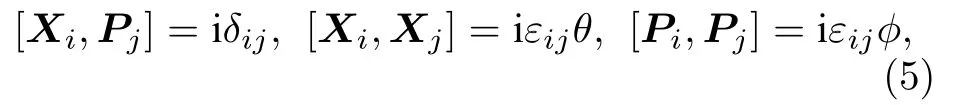
其中,εij是反对称张量,θ和ϕ是非对易参数. 非对易相空间中的坐标和动量是缺乏对称性的.

文献[26, 27]研究的二维耦合谐振子模型的哈密顿量仅含有坐标耦合项, 为了使讨论更具有一般性, 本文设二维耦合谐振子的哈密顿量是

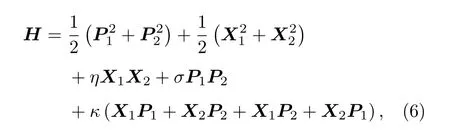
其中,η是坐标坐标耦合参数,σ是动量动量耦合参数,κ是坐标动量交叉耦合参数, 这些耦合参数可以表示相互作用的强度. 哈密顿量H包含了所有的可能的耦合项, 可以作为二维耦合谐振子的一般模型. 通过(5)式得到

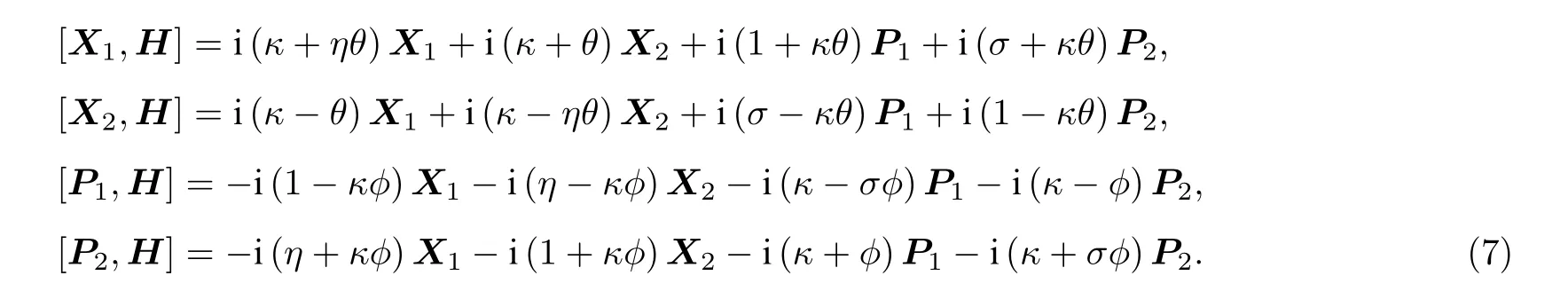
可以看出算符集合{X1,X2,P1,P2}在与H对易关系的运算中是封闭的, 因此设不变本征算符为

其中,α,β,γ,ε是待定的系数. 算符O满足如下方程

将(6)式和(8)式代入(9)式解得

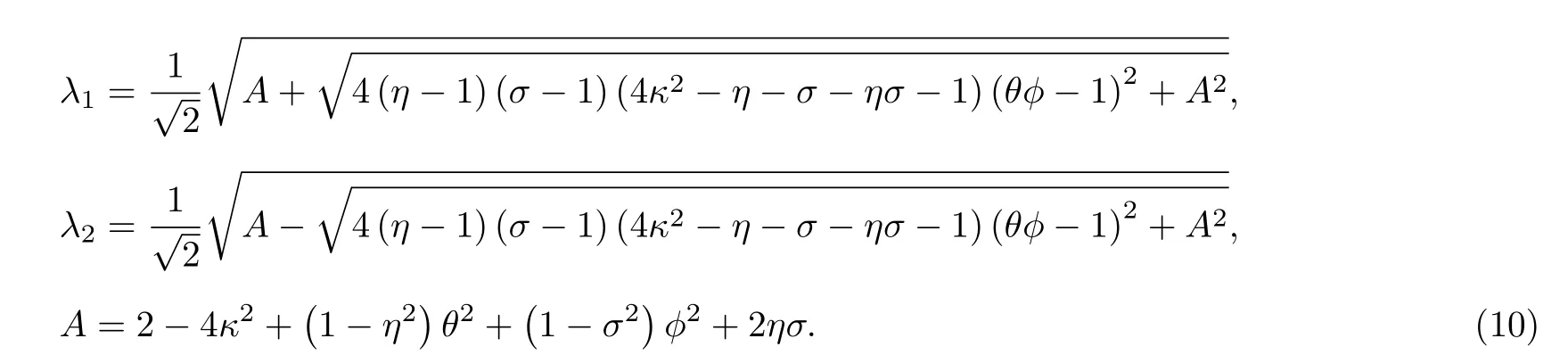
根据IEO 方法,λ1和λ2为系统的能级差 ΔE. 由此可以得到二维耦合谐振子的非对易能级为

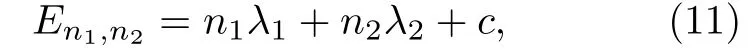
其中,n1,n2是量子数, 且是非负整数;c是常数.我们所熟知的通常对易空间中二维谐振子的能级是En1,n2=n1+n2+1 , 且能级除基态外都是简并的. 考虑对(11)式取极限θ →0 ,ϕ →0 , 并且忽略耦合项可以得到通常二维谐振子的能级, 所以取c= 1.

4 讨 论

假设所有耦合参数都为0, 则二维非耦合谐振子的非对易能级可以写为

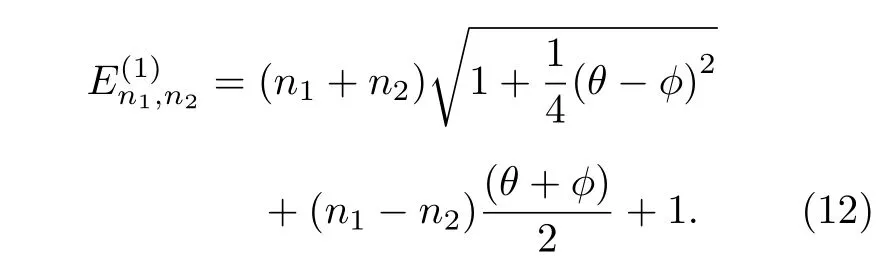
由(12)式可以看出二维非耦合谐振子的非对易能级是非简并的. 为了展示非对易性对该能级的影响, 我们举一个具体的例子, 即当n1+n2=2 时,各个能级的值如表1 所示.

表1 能级 的值(n1+n2 = 2, η= σ = κ = 0)Table 1. Values of E (n1+n2 = 2, η = σ = κ = 0).

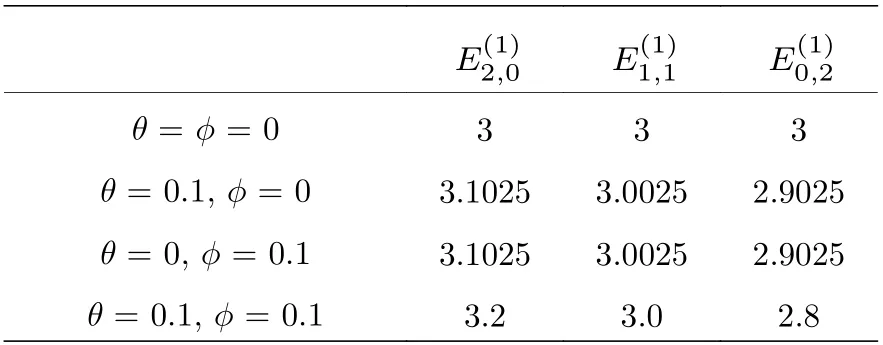
表1 能级 的值(n1+n2 = 2, η= σ = κ = 0)Table 1. Values of E (n1+n2 = 2, η = σ = κ = 0).

E(1)2,0E(1)1,1E(1)0,2 θ = φ = 0333 θ = 0.1, φ = 03.10253.00252.9025 θ = 0, φ = 0.13.10253.00252.9025 θ = 0.1, φ = 0.13.23.02.8

从表1 可以看到, 第2 行当非对易参数θ和ϕ都为0 时, 能级是简并的, 这与通常对易空间中二维谐振子的能级情况是一致的. 而表中第3 至5 行当参数θ和ϕ不为0 时, 能级会出现劈裂. 第3 行参数θ对能级的影响程度和第4 行参数ϕ的影响程度是一样的, 即以相同的数值破坏能级的简并. 第5 行中参数θ和ϕ的同时作用会加大能级劈裂的程度. 这些结果表明虽然对易空间二维谐振子存在对称性, 具体表现为能级的简并, 但是非对易性能够破坏这种对称性, 并产生了能级劈裂.

当非对易参数θ和ϕ都为0 时, 二维耦合谐振子的能级可以写为

为了展示耦合谐振子能级的变化, 仍以n1+n2=2时的能级为例, 具体能级值如表2 所示.

表2 说明即使非对易参数θ和ϕ为0, 但耦合参数η,σ和κ不为0, 能级也会出现劈裂, 即耦合项的加入同样会破坏能级的对称性, 使得能级变成非简并的. 表2 第2 至4 行表示系统只包含一类耦合项时能级的变化, 可以看出坐标耦合参数η和动量耦合参数σ对能级的影响程度是一样的, 但是坐标动量交叉耦合参数κ对能级的影响小于η和σ.表2 第5 至7 行表示系统包含两类耦合项时能级的变化. 其中第5 行是系统同时包含坐标耦合和动量耦合时的能级, 与第2 至4 行比较可以发现当系统同时包含两个耦合项时能级劈裂的程度变大了.第6 行是系统同时包含坐标耦合和坐标动量交叉耦合时的能级, 与第5 行比较可以发现坐标动量交叉耦合项的出现使能级劈裂的程度变小了. 第7 行是系统同时包含动量耦合和坐标动量交叉耦合时的能级, 与第6 行的结果是一样的. 表2 第8 行是系统同时包含坐标耦合、动量耦合和坐标动量交叉耦合时的能级, 与第5 至7 行比较可以发现当系统同时包含三类耦合项时能级劈裂的程度进一步增大了.

表2 能级 的值(n1+n2 = 2, θ = φ = 0)Table 2. Values of E(n1+n2 = 2, θ = φ = 0).

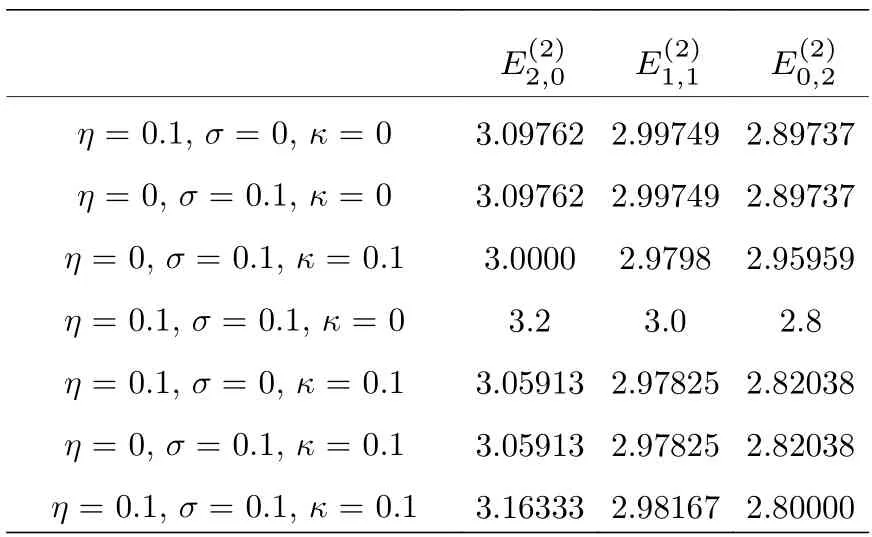
表2 能级 的值(n1+n2 = 2, θ = φ = 0)Table 2. Values of E(n1+n2 = 2, θ = φ = 0).

E(2)2,0E(2)1,1E(2)0,2 η = 0.1, σ = 0, κ = 03.09762 2.99749 2.89737 η = 0, σ = 0.1, κ = 03.09762 2.99749 2.89737 η = 0, σ = 0.1, κ = 0.13.0000 2.9798 2.95959 η = 0.1, σ = 0.1, κ = 03.23.02.8 η = 0.1, σ = 0, κ = 0.13.05913 2.97825 2.82038 η = 0, σ = 0.1, κ = 0.13.05913 2.97825 2.82038 η = 0.1, σ = 0.1, κ = 0.13.16333 2.98167 2.80000

能级En1,n2(n1+n2=2) 随参数θ的变化情况如图1 所示. 从图1 可以看到,E2,0随着θ的增加而增加.E1,1随着θ的变化比较平缓, 总体趋势是逐渐增加的.E0,2是随着θ的增加先减小后增加.而且图1中θ=1 的点是能级的最小值. 这是因为当θϕ=1 时(11)式中的第2 项等于0. 另外, 当θ取较大值时, 能级E1,1和E2,0呈现出线性变化的趋势.能级En1,n2随参数ϕ的变化情况与图1 相同, 这里不再赘述.

图1 En1,n2 随θ 的变化曲线(n1 + n2 = 2, φ = 1, η =0.5, σ = 0.5, κ = 0.5)Fig. 1. En1,n2 versus θ (n1 + n2 = 2, φ = 1, η = 0.5, σ =0.5, κ = 0.5).

5 结 论

本文构造了同时包含坐标坐标、动量动量及坐标动量交叉的所有耦合项的二维耦合谐振子的模型, 并在非对易相空间中研究其能谱的特性. 首先,用IEO 方法计算得到了二维耦合谐振子非对易能谱的解析解. 从(10)式和(11)式可以看出, 系统能谱是与耦合参数和非对易参数有关的. 其次, 由于该解析解形式比较复杂, 所以对其进行了分类讨论. 以图表的形式详细分析了耦合参数和非对易参数对能谱的影响, 得到以下结果. 1)受到非对易参数的影响能级会出现劈裂. 一般对易空间中二维谐振子具有较高的对称性, 表现在其能级除基态外是简并的. 然而, 非对易性的出现破坏了这种对称性,使得能级出现了劈裂. 由于非对易相空间中坐标和动量算符的形变导致了二维耦合谐振子的非对易能级出现非简并的情况. 这是很重要的性质, 为我们检验空间的非对易性提供了可能的途径. 2)非对易参数θ可以使n1̸=0 的能级值增加, 而且随着θ值的不断增加, 能级会随其线性变化. 但是对于n1=0的能级,θ使其值先减少后增加. 参数ϕ也有同样的效果. 3)如果对非对易能谱取极限值, 即θ →0,ϕ →0 , 结果会与通常对易空间中的二维谐振子的能谱一致. 4)受到耦合参数的影响, 能级会出现劈裂. 耦合项表示谐振子两个维度之间的相互作用, 这种相互作用引起了能级的移动, 导致能级出现非简并的情况. 而且当系统包含的耦合种类增多时, 能级劈裂的程度也会增大. 同时发现坐标耦合参数η和动量耦合参数σ对能级的影响程度是一样的, 但是坐标动量交叉耦合参数κ对能级的影响小于η和σ.