基于时域法的经编机电子横移系统动态性能

王博浩， 郗欣甫， 孙以泽

(东华大学 机械工程学院， 上海 201620)

近年来，由于电子横移经编机能够满足经编布料产品周期短、品种多、批量小的市场竞争要求[1]，国内电子横移经编机得到飞速发展，但与国外仍存在较大差距，主要表现在国内高速经编机转速和稳定性不如国外同类产品[2-3]。目前电子横移经编机的生产转速远远不如花盘凸轮式横移经编机，因此电子横移系统的性能成为制约经编机生产效率的主要因素之一[4-5]。

经编机电子横移系统综合了电力电子、计算机控制、机械工程等多领域的交叉技术[6]，其电气部分与机械部分存在一定程度的耦合，导致经编机电子横移系统的理论研究与参数整定存在一定的难度，因此有必要建立精确的电子横移系统控制模型，以期为该系统的理论研究与性能优化提供一定的理论依据。

国内学者对经编机电子横移系统展开了一系列理论研究。翟云[4]建立经编机电子横移系统的数学模型，并利用该数学模型推导出系统的闭环传递函数。张琦[5]建立经编机电子横移系统整体结构的动力学模型，并使用MATLAB/Simulink软件进行仿真分析。郑静等[6]对电子横移系统的伺服驱动部分和机械部分进行数学建模，并使用MATLAB/Simulink软件进行仿真研究。然而，这些研究在对经编机电子横移系统进行建模时，大多数未考虑逆变器环节、反电动势环节、电流滤波环节、速度滤波环节以及电气部分与机械部分之间的耦合，导致理论数学模型无法展现实际系统的动态性能。

建立经编机电子横移系统的电流环、速度环、位置环，以及机械传动部分的数学模型，采用时域法对系统进行降阶处理，分析电子横移系统参数对其动态性能的影响以及电子横移系统高速运行时出现振荡现象的原因，并在MATLAB/Simulink软件中进行仿真研究，通过试验检验了理论分析的可靠性，研究结果有望为电子横移系统的动态性能研究以及系统设计提供理论基础。

1 经编机电子横移系统简介

经编机电子横移系统一般采用交流伺服旋转电机作为驱动装置，通过滚珠丝杆将电机的旋转运动转化成直线运动，从而驱动导纱梳栉实现往复横移运动[7]，如图1所示。由于位置监测装置不易安装在横移梳栉上，并且梳栉横移时产生的振动会影响位置监测装置信号的稳定性和精度，因此一般电子横移系统采集电机轴端的输出转角作为系统的位置检测信号。经编机电子横移系统中常采用电流环、速度环、位置环三闭环控制策略，属于典型的交流伺服控制系统。

图1 经编机电子横移系统结构Fig.1 Electronic shogging system structure of warp knitting machine

2 经编机电子横移系统的数学模型

经编机电子横移系统主要由伺服系统和机械系统组成，其中伺服电机直接驱动丝杆，进而驱动梳栉进行横移。采集电机轴的输出转角作为系统的位置反馈。

2.1 电子横移系统电气数学模型

电子横移系统采用永磁同步电机(permanent magnet synchronous motor, PMSM)作为驱动装置，电气部分一般采用电流环、速度环、位置环三闭环控制策略[8-10]，其数学模型结构框图如图2所示。图2中：Kp为位置调节器增益；Kfp为位置检测增益；Tv为速度滤波时间常数；Kfv为速度检测增益；Kv为速度调节器增益；τv为速度调节器积分时间常数；Ti为电流滤波时间常数；Kfi为电流检测增益；Ki为电流调节器增益；τi为电流调节器积分时间常数；Tpwm为逆变器时间常数；Kpwm逆变器增益；R为电枢绕组等效电阻；Ts为电枢绕组电气时间常数；Kt为力矩系数；Ke为反电动势系数；Jm为电机的等效转动惯量。

图2 永磁同步电机三环控制结构框图Fig.2 Block diagram of three-loop control on PMSM

(1)电流环。从稳态要求来看，希望电流环稳态时无静差；从动态特性来看，希望电流环跟随性好，超调量小。因此采用PI控制器作为电流环调节器，将电流环校正成典型的I型环节。忽略电机轴上负载力矩TL和反电动势对电流环的影响。由于电机的电气时间常数较大，为提高电流环响应速度，根据零极点对消方法，一般取电流控制器积分时间常数等于电气时间常数[11]，即Ti=Ts，于是可以将电流环等效为二阶环节，其闭环传递函数为

(1)

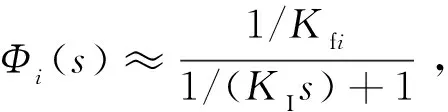
(2)

(3)

(3)位置环。位置环以速度环为内环，一般采用比例控制器作为位置环调节器，此时系统为I型系统，当系统的输入信号为阶跃信号时，系统的稳态误差为0。在电流环和速度环参数确定的情况下，可以通过参数调试法或根轨迹法来确定位置调节器的增益。

2.2 电子横移系统机械传动数学模型

电子横移系统的结构如图3所示。经编机电子横移系统的机械系统由联轴器、滚珠丝杆、钢丝绳、球铰、导纱梳栉等部件组成[13]。经编机电子横移机构通过滚珠丝杆将伺服电机的旋转运动转换为导纱梳栉机构的往复横移运动。

图3 电子横移系统结构简图Fig.3 Structural diagram of electronic shogging system

依据动力学等效变换原理，可以将整个机械传动机构的惯量、刚度、阻尼和负载干扰转矩都折算到丝杆上，简化得到如图4所示的二惯量系统[14-15]。

由图4所示的二惯量系统，建立如式(4)所示的方程组。

(4)

图4 二惯量系统动力学模型Fig.4 Dynamic model of two-mass system

式中：θm为电机轴输出的角度；Te为电机输出的电磁转矩；Jm为电机的转动惯量；Tw为传动轴转矩；Kl为各机械传动部件折算到丝杠上的扭转刚度；Jl为各机械传动部件折算到丝杠上的转动惯量；Bl各机械传动部件折算到丝杠上的黏滞阻尼系数；θl为丝杆输出的转角；Tl为折算到丝杠上的干扰转矩，Xl为梳栉的直线位移输出；Pb为丝杆导程。

综上，最终得到机械传动部分的结构图，如图5所示。

图5 机械传动部分的结构框图Fig.5 Block diagram of mechanical transmission

2.3 电子横移系统整体模型

将PMSM三环伺服控制的结构框图和机械传动部分的结构框图整合到一起，即可得到经编机电子横移系统整体的结构框图，如图6所示。由此可见，经编机电子横移系统属于典型的半闭环伺服进给系统。

图6 电子横移系统结构框图Fig.6 Block diagram of electronic shogging system

3 经编机电子横移系统仿真

基于MATLAB/Simulink软件以仿真的方式验证图6所示模型的准确性，并对电子横移系统中各参数对系统性能的影响进行分析。由于丝杆的输出转角θl与梳栉的直线位移输出Xl存在倍数关系，为了便于观测系统的阶跃响应，仿真中采用θl作为系统的输出。

3.1 仿真参数

根据实际工程应用情况，伺服电机选用台达ECMA-C1-09-10-ES型，并按照第2.1节的方法确定伺服驱动器的参数。设置经编机电子横移系统仿真参数如表1所示。

表1 电子横移系统仿真参数Table 1 Simulation parameters of electronic shogging system

3.2 位置环动态性能分析

位置环主导零极点分布如图7所示，位置环系统与其降阶系统的单位阶跃响应曲线如图8所示。位置环上升时间tr=1.83 ms，峰值时间tp=4.04 ms，调整时间ts=3.32 ms，最大超调量σ=0.11%。

图7 位置环主导零极点分布Fig.7 Distribution of domain poles and zeros of position loop

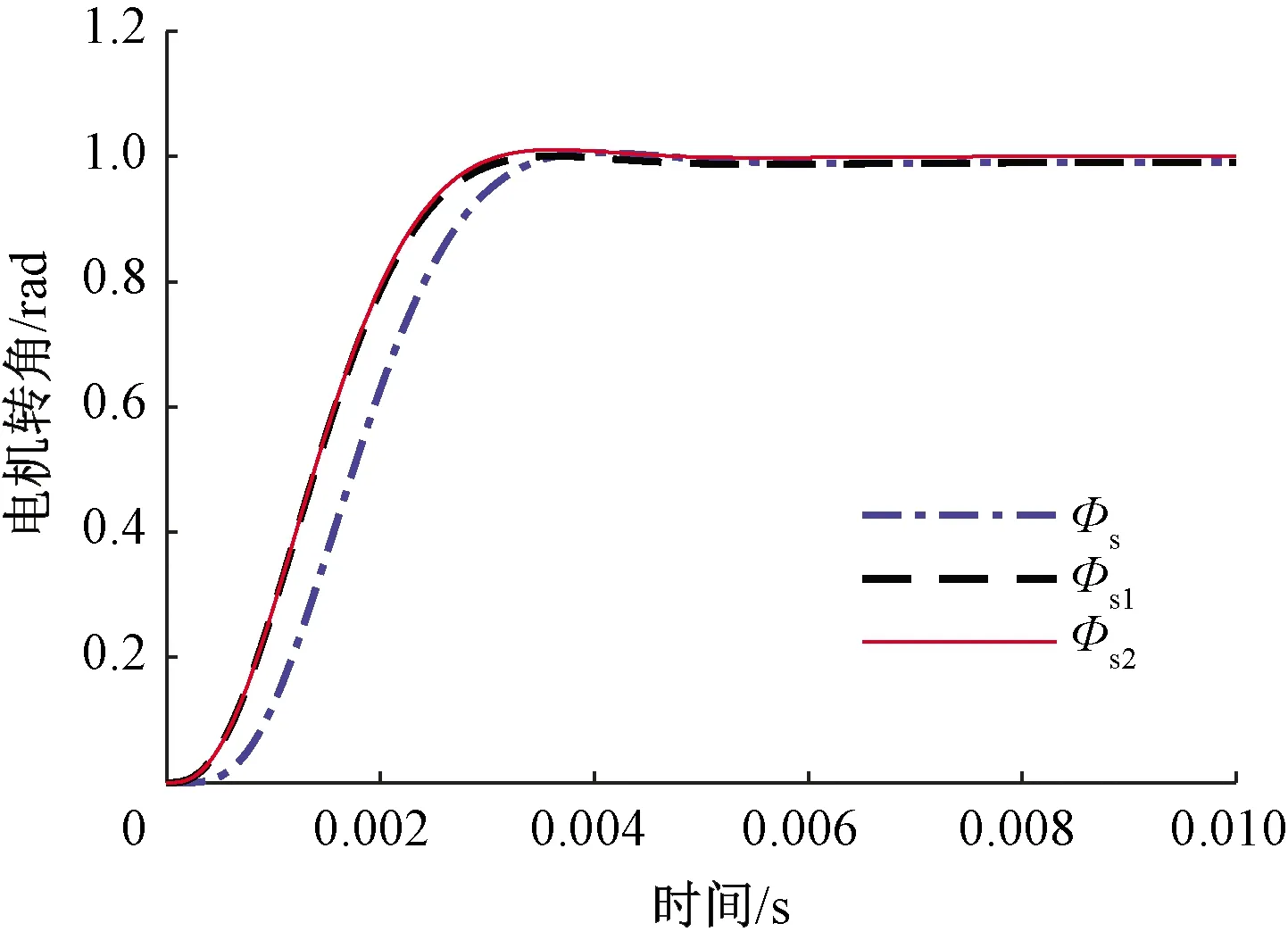
图8 位置环及其降阶系统的单位阶跃响应曲线Fig.8 Step responses of position loop and its reduced order systems

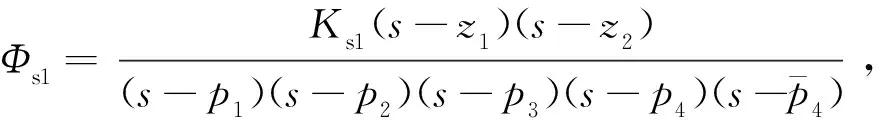
3.3 机械传动部分的加入对系统的影响

电子横移系统主导零极点分布如图9所示，电子横移系统与其降阶系统的单位阶跃响应曲线如图10所示。加入机械传动装置之后，系统上升时间tr=3.36 ms，峰值时间tp=8.58 ms，最大超调量σ=11%。根据经验，横移单次移针误差超过5%以上便会出现擦针，因此误差范围取±5%，系统调整时间ts=14.2 ms。

图9 电子横移系统的主导零极点分布Fig.9 Distribution of domain poles and zeros of electronic shogging system

图10 电子横移系统及其降阶系统的单位阶跃响应曲线Fig.10 Step responses of electronic shogging system and its reduced order systems

3.4 位置调节器增益对系统的影响

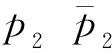
图11 随Kp值变化的系统主导极点轨迹Fig.11 Locus of system domain pole varying with Kp

当位置调节器增益Kp取不同值时，电子横移系统的单位阶跃响应曲线如图12所示。结合上述分析可知，当Kp=100时，系统的主导极点为靠近虚轴、阻尼比小的极点，因此此时系统响应慢，超调量小；随着Kp的增加，系统的主导极点逐渐远离虚轴，且阻尼比增加，因此当Kp=600时，系统响应速度变快，超调量增加；但随着Kp的继续增大，机械系统引入的共轭极点将逐渐靠近虚轴，因此当Kp=1 000时，系统会发生剧烈的机械谐振现象。

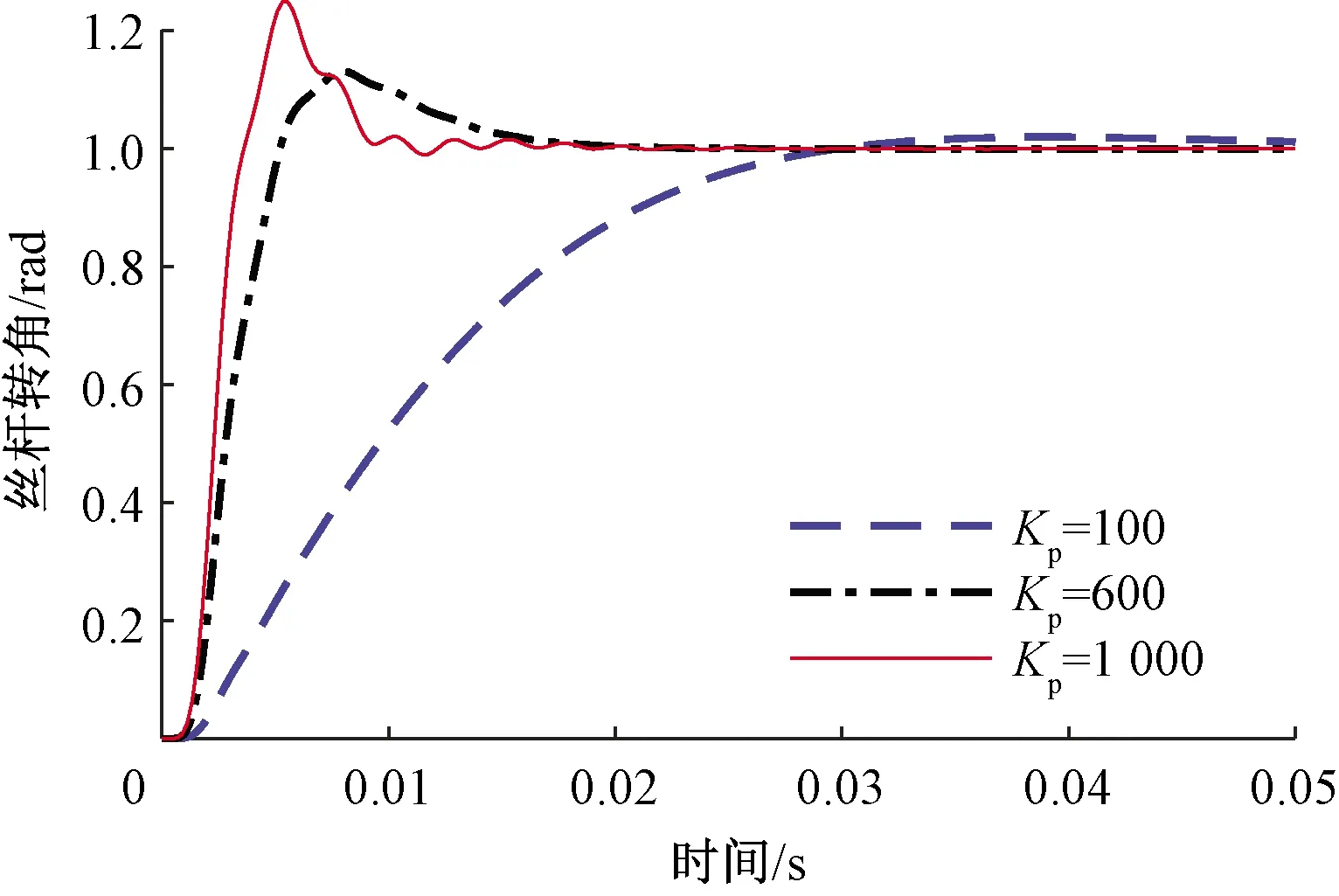
图12 不同Kp值下的系统单位阶跃响应曲线Fig.12 System step responses under different Kp values

3.5 速度环增益对系统的影响

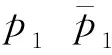
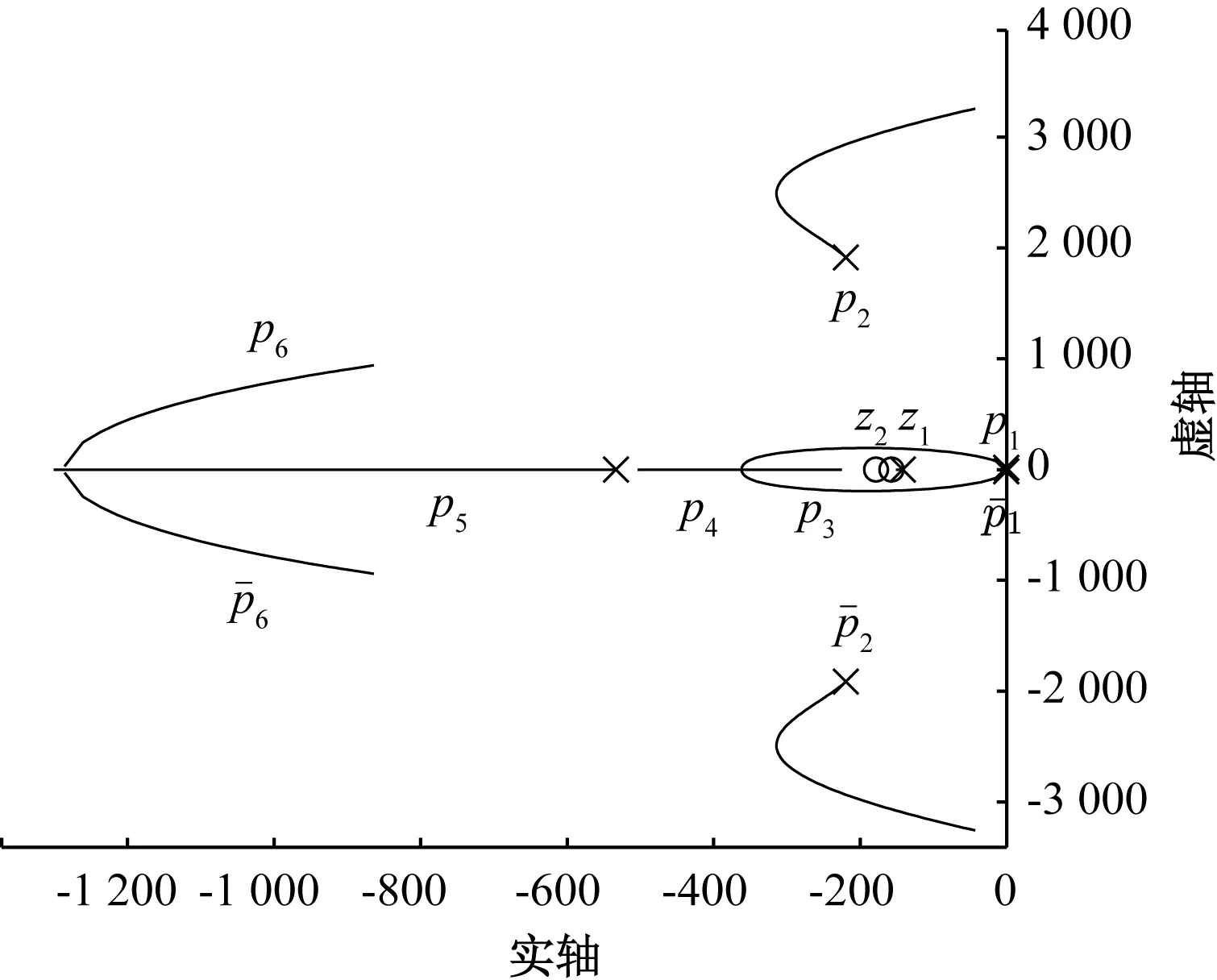
图13 随Kv值变化的系统主导极点轨迹Fig.13 Locus of system domain pole varying with Kv

当速度调节器增益Kv取不同值时，电子横移系统的单位阶跃响应曲线如图14所示。结合上述分析可知，当Kv=0.1时，系统的主导极点为靠近虚轴、阻尼比较大的极点，因此此时系统响应慢，超调量大；随着Kv的增大，系统的主导极点逐渐远离虚轴，阻尼比减小，因此当Kv=0.5时，系统响应速度变快，超调量减小；但随着Kv的继续增大，机械系统引入的共轭极点将逐渐靠近虚轴，因此当Kv=0.9时，系统会发生剧烈的机械谐振现象。

图14 不同Kv值下的系统单位阶跃响应曲线Fig.14 System step responses under different Kv values

4 试验验证

以7梳RD7-EL型拉舍尔双针床经编机为例进行试验验证。在双针床经编机中，主轴每转一圈，横移完成2个横列的编织。由于机械结构的缘故，经编机的最高机速一般取决于横移梳栉针前所允许的横移角度，GB1后针床针前所允许的横移角度最小，为36°。在GB1梳栉上执行横移工艺1-0/1-2//，通过在伺服驱动器中设置不同的位置调节器增益和速度调节器增益，并使用Trio控制器自带的示波器监测横移工艺的响应曲线。

不同Kp值下GB1横移工艺的响应曲线如图15所示。其中：图15(a)中，横坐标每格代表20 ms，当Kp=400时，系统的响应速度慢，超调量较小，针前横移时间约为24 ms；图15(b)中，横坐标每格代表10 ms，当Kp=800时，系统的响应速度变快，针前横移时间约为10 ms，但此时系统运行过程中伴随着强烈的振荡，容易发生擦针现象。

图15 不同Kp值下GB1横移工艺的响应曲线Fig.15 GB1 shog craft responses under different Kp values

不同Kv值下GB1横移工艺的响应曲线如图16所示。其中：图16(a)中，横坐标每格代表20 ms，当Kv=0.3时，系统的响应速度慢，超调量较大，针前横移时间约为20 ms；图16(b)中，横坐标每格代表10 ms，当Kv=0.8时，系统的响应速度变快，针前横移时间约为12 ms，但此时系统运行过程中伴随着强烈的振荡，容易发生擦针现象。

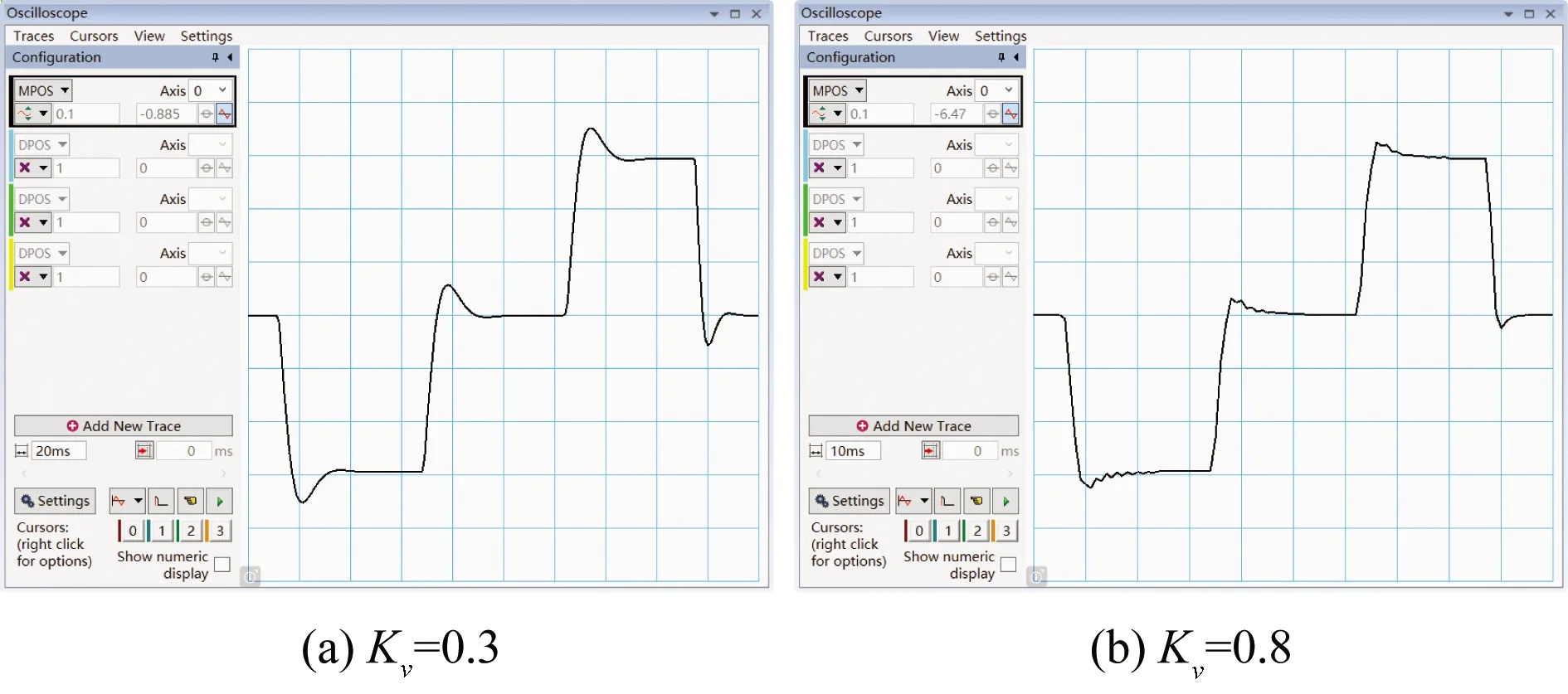
图16 不同Kv值下GB1横移工艺的响应曲线Fig.16 GB1 shog craft responses under different Kv values

5 结 论

(1)建立经编机电子横移系统的数学模型，采用 MATLAB/Simulink软件验证模型的准确性和系统的稳定性，仿真结果能够很好地满足经编机电子横移系统的动态性能要求。

(2)采用时域主导零极点方法分析得出，加入机械传动部分将使得电子横移系统响应变慢，超调量增大，并且引入一对靠近虚轴、阻尼比极小的共轭复根，使得系统有产生高频振荡的趋势。

(3)时域法仿真分析结果表明，适当增大位置调节器增益和速度调节器增益有利于提高电子横移系统的响应速度，增大系统的带宽，但过大的位置调节器增益和速度调节器增益将引发机械谐振现象，使得系统发生振荡，不利于系统的稳定性。