贵州省气象干旱特征时空演变规律及联合发生概率分析

李宝玉,朱晓萌,冯凯,张泽中,崔振华

(1.河南水利与环境职业学院,河南 郑州450045;2.贵州省水利工程建设质量与安全中心,贵州 贵阳550002;3.华北水利水电大学 水利学院,河南 郑州450046;4.黄河勘测规划设计研究院有限公司,河南 郑州 450003)

旱灾是由于水分收支不平衡导致的一种自然灾害,具有持续时间长、破坏力强等特点,广泛发生于世界各地[1]。旱灾的影响因素众多,其发生演变过程较为复杂,一旦发生就会对当地的生态环境、粮食安全、经济社会可持续发展等构成严峻威胁[2]。据统计,全球范围内气象灾害占所有自然灾害的70%左右,而旱灾占到气象灾害的一半以上[3]。自20世纪以来,全球70%以上的国家受到不同程度的旱灾威胁,20亿以上的人口遭受旱灾影响,由旱灾造成的年均直接经济损失高达80亿美元,占所有气象灾害损失的50%[4]。近年来,随着全球气候问题日趋严重,我国干旱的发生频率及强度显著增加[5-6],亟需开展干旱时空演变特征及风险分析,为区域防旱抗旱及水资源管理提供科学依据。

干旱诱发因素众多,其发展过程循序渐进,发生和结束时间难以监测,造成研究结果比较抽象。鉴于数据的易获得性和可操作性,学者们通常采用干旱指标来监测干旱的严重程度,以定量描述干旱的发展过程,提高干旱的定量化监测能力。根据国际上普遍认可的干旱分类,干旱指数包括气象干旱指标、水文干旱指标、农业干旱指标和社会经济干旱指标4种[7-8]。气象干旱常用的干旱指标有标准化降水指数(Standardized Precipitation Index,SPI)、帕默尔干旱指数(Palmer Drought Severity Index,PDSI)、标准化降水蒸散指数(SPEI)等。其中,SPEI不仅考虑了干旱对温度的敏感性，而且具有空间可比性和多时间尺度的特征,弥补了SPI和PDSI在干旱监测中的不足[9]。SPEI在区域干旱研究中应用广泛,赵平伟等[10]对SPEI和SPI在滇西南地区干旱监测中的应用效果进行了对比,结果表明SPEI对气候变化背景下的区域干旱监测结果较为准确;王林等[11]基于拟合优度检验、SPEI与SPI和PDSI之间的关系以及与历史干旱事件对比结果等,全面分析了SPEI对中国干旱状况评估的准确性,结果表明SPEI比SPI能够更精确地刻画干旱特征;TAN C P等[12]基于SPEI和SPI分析了宁夏回族自治区的干旱时空演变特征,结果发现SPEI能够更加精确地反映研究区的干旱状况。

西南地区是我国受干旱灾害影响最严重的地区之一,几乎每年都会发生不同严重程度的干旱事件[13]。2009—2012年,西南五省(云南省、四川省、重庆市、贵州省和广西省)遭受了严重干旱,造成约1.2×108亩的耕地受影响,导致作物大幅减产及2 500万人和1 800万头牲畜饮水困难,直接经济损失超过400亿人民币,这是自有气象观测记录以来西南地区发生的最严重干旱事件[14-15]。贵州省地处我国西南腹地,地形地貌极其复杂,土层厚度较小,蓄水能力较差,降水、气温等气象要素时空分布不均,致使旱灾成为该地区主要的自然灾害之一[16]。

本文以贵州省为研究区,以SPEI来表征气象干旱,基于改进的Mann-Kendall检验法、优化的游程理论、Copula函数等方法分析贵州省干旱时空演变及风险特征,研究结果可为贵州省干旱监测评估及旱灾风险决策提供理论依据。

1 研究区概况及数据来源

本文选取贵州省为研究对象,其位于我国西南内陆地区,24°37′～29°13′N,103°36′～109°35′E。贵州境内地势西高东低,自中部向北、东、南三面倾斜,平均海拔1 100 m,素有“八山一水一分田”之说。全省地形地貌复杂多变,包括高原、山地、丘陵和盆地4种基本类型,总面积17.62万km2,其中92.5%的面积为山地和丘陵[17]。贵州省属亚热带季风气候,冬季平均气温集中在3～6 ℃,夏季平均气温集中在22～25 ℃,多年平均气温15 ℃左右,年平均降雨量1 179 mm[18]。大气环流及地形对贵州省气候环境的影响较大,导致气候不稳定,干旱事件频发,对农业生产造成了严重危害。

本研究选取1960—2017年贵州省境内17个气象观测站点的逐月平均气温、最高气温、最低气温、降水、风速、太阳辐射、日照时数、实际水汽压、相对湿度及地表大气压等气象资料,数据来自中国气象局国家气候中心(http://data.186 cma.cn/)以及贵州省水利科学研究院。所选站点具有较高的代表性,能够反映贵州实际,数据整体质量较好,其中个别缺失的气象数据采用多重线性回归模型插补。研究区概况及站点分布如图1所示。

图1 研究区范围及站点分布图

2 研究方法

2.1 标准化降水蒸散指数(SPEI)

当前，气象干旱研究中较为常用的干旱指标包括标准化降水指数(SPI)、帕尔默干旱指数(PDSI)以及标准化降水蒸散指数(SPEI),但SPI仅以降水为基础,忽略了气温和蒸发量对干旱的影响,PDSI存在时间尺度单一、不具有空间可比性等缺点[19-20],而SPEI不仅考虑了干旱对温度的敏感性，还具有空间可比性和多时间尺度的特征[21]。因此,本文选取SPEI来表征气象干旱情况,其原理是基于降水与潜在蒸散发之间的差异程度来表征干旱状况。计算步骤如下:首先,计算降水量和潜在蒸发量之间的差额；然后，对差值序列进行拟合，求得累积概率密度函数；最后，将其转化为标准正态分布，求得SPEI值。SPEI的干旱等级划分情况见表1[22]。

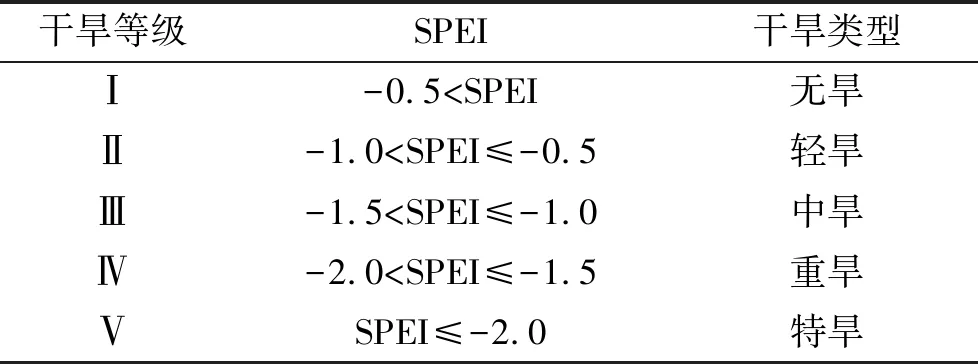
表1 标准化降水蒸散指数的干旱等级划分

2.2 改进的Mann-Kendall(MMK)检验

传统的Mann-Kendall(MK)趋势检验法是基于时间序列保持随机性和独立性的假设条件。实际上，由于计算使用的气象要素时间序列往往存在自相关性,会对检验结果的可靠性造成一定影响[23]。基于此,一种更合理的时间序列变化趋势非参数检验方法,即改进的Mann-Kendall(Modified Mann-Kendall,MMK)趋势检验方法应运而生,该方法可以消除时间序列中的自相关成分,使趋势检验结果的可靠性显著提高,其计算步骤可参考文献[24-25]。对于趋势统计量Z值,当Z值大于零时，表示时间序列呈上升趋势；当Z值小于零时，表示时间序列呈下降趋势；当|Z|分别大于1.64、1.96和2.58时,表示时间序列的变化趋势分别通过p=0.1、p=0.05和p=0.01的显著性检验。

2.3 优化的游程理论

游程理论在干旱特征识别中应用较为广泛。传统的游程理论通常设置1个干旱阈值水平来识别干旱特征变量,但在实际应用中，存在一场较为严重的干旱事件可能被极少数短历时非干旱事件分割为多场一般干旱事件的状况,导致实际的干旱强度降低,造成识别结果精度不高[26]。因此,本文采用优化的游程理论方法,即将干旱特征识别的阈值水平增加到3个,以提高干旱识别结果的可靠性,进而基于优化的游程理论从干旱指数序列中识别干旱事件，并提取干旱历时和干旱烈度2个特征变量。干旱历时表示一次干旱事件从开始到结束所持续的时间,干旱烈度反应该场干旱事件中的总缺水量。设置3个干旱发生阈值X0、X1和X2(X代表SPEI值),干旱事件的识别过程如下:

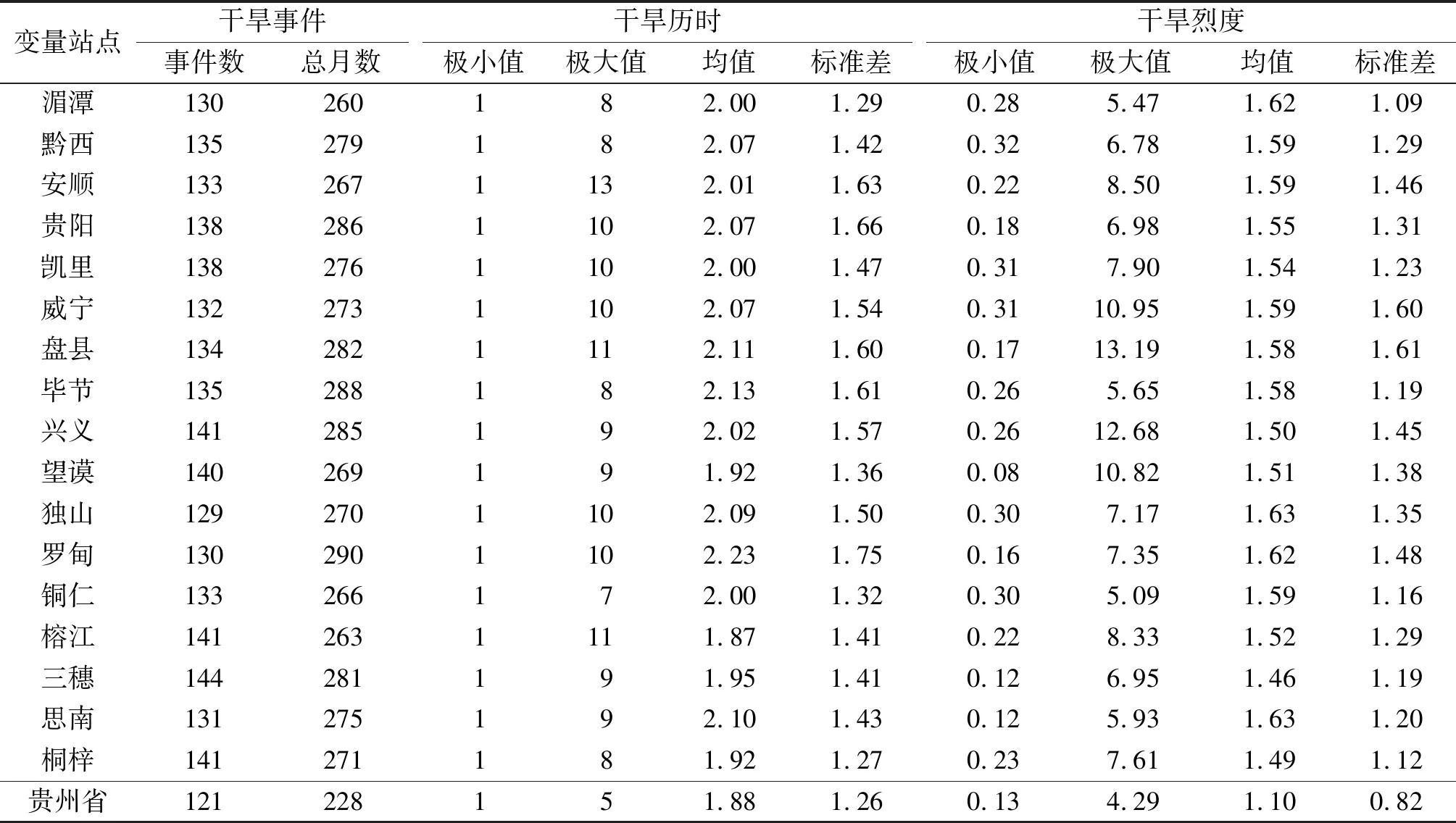
1)根据干旱发生阈值X1，初步判断是否发生干旱事件,若SPEI值

2)对于干旱历时等于1个月，且严重程度未达到干旱阈值X2的干旱事件,则认为该月没有发生干旱,将其剔除;

3)若相邻2次干旱事件时间间隔等于1个月，且该月的SPEI值小于X0,则将这2次干旱事件合并,干旱历时等于2次干旱历时之和加1,干旱烈度等于2次干旱事件烈度之和,否则认为是2次单独的干旱事件。

本研究中,首先计算SPEI值以监测评估干旱状况,然后利用优化的游程理论提取1960—2017年贵州省的干旱事件特征信息,基于提取结果采用MMK、Copula等方法分析研究区干旱特征的演变规律及发生概率。

3 结果与分析

3.1 贵州省气象干旱严重程度的演变特征

基于月尺度SPEI,利用优化的游程理论对各站点及贵州全省1960—2017年干旱事件进行识别，并提取干旱特征变量,统计结果见表2。

表2 贵州省1960—2017年各站点气象干旱事件及特征变量统计分析

从表2中可以很直观地看出：三穗站的干旱事件数最多，为144场,贵州全省的干旱事件数最少，为121场；所有站点干旱事件的持续时间总月数集中在228～290个月；单场干旱事件持续时间最长为13个月,发生在安顺站;干旱烈度最大值为13.19,发生在盘县站,这与WANG Y等[27]的研究结果具有较高的一致性。

基于干旱事件识别结果,利用干旱历时和干旱烈度定量表征和评价干旱严重程度的时空演变特征,结果如图2所示。由图2可知,贵州省发生的气象干旱平均持续时间集中在1.8～2.3个月,贵州省遵义市北部、黔东南及黔西南部分区域的干旱持续时间较短,表明这些区域的干旱发生频率较高;贵州省三穗县附近区域干旱事件持续时间呈现显著增加的趋势(p=0.1);贵州省1960—2017年干旱烈度的整体空间分布特征与干旱历时比较类似,干旱烈度值集中在1.4～1.7,干旱烈度相对较低的区域分布在贵州省遵义市西北部、黔西南及黔东南地区,除了上述区域外其他地区的干旱严重程度相对较高;与干旱历时相比,干旱烈度变化趋势的空间特征有明显差异,贵州省东北及西南地区有轻微增加的趋势,三穗县和靖远县附近区域呈现显著上升趋势(p=0.05),而贵州省的黔南及毕节市干旱烈度呈现下降趋势。上述研究结果与WANG Y等[27]关于贵州省干旱时空分布特征的分析结果保持一致。综上所述,贵州省近58年来干旱事件频繁发生,且经历了长期的较为严重的气象干旱事件。贵州省东部、黔西南及遵义市西北地区的气象干旱事件具有发生频繁、持续时间短、强度弱的特点,并存在干旱持续时间延长和严重程度增加的趋势。在全球气候变暖的影响下,这些干旱事件多发地区的干旱灾害可能会越来越严重。

图2 贵州省1960—2017年干旱历时、烈度及其变化趋势空间分布特征

3.2 干旱特征变量边缘分布选择

基于Copula函数进行干旱频率分析之前,需要分析各组变量间的相关性,其相关性程度是选择Copula函数以及参数估计的基础。贵州省1960—2017年121场气象干旱历时和烈度之间的相关显著性检验结果见表3。从表3中可以看出,干旱历时和烈度之间具有较强的相关性，且通过了p=0.01的显著性检验,表明干旱历时和烈度之间的相互依赖性很大,采用Copula函数进行联合分布建模的频率分析是合理的。

表3 干旱历时和烈度间的Pearson、Kendall和Spearman相关系数

基于Kolmogorov-Smirnov(K-S)和Anderson-Darling(A-D)拟合优度检验方法,从伽马分布(Gam)、对数正态分布(LogN)、韦伯分布(Wb)、指数分布(Exp)、广义极值分布(GEV)和广义帕累托分布(GP)6种备选分布函数中确定干旱历时和烈度的最优边缘分布类型,采用极大似然法进行参数估计。在p=0.05的显著性水平下,如果拟合结果通过K-S检验,则选择A-D统计量最小的分布作为干旱特征变量的最优分布,如果未通过K-S检验,则直接舍弃。

气象干旱历时和烈度的最优边缘分布函数及参数见表4。从表4可知,在通过K-S检验的基础上,干旱历时和烈度对应的GP分布和LogN分布的A-D检验统计量值最小,则干旱历时和烈度的最优边缘分布函数分别为GP分布和LogN分布。

表4 气象干旱历时和烈度的最优边缘分布函数及参数

干旱历时和烈度最优边缘分布的经验频率与理论频率的拟合效果如图3所示。由图3可知,数据点均集中在1∶1直线附近,表明干旱特征变量最佳拟合分布的理论与经验概率具有良好的对应关系。

图3 气象干旱历时和烈度的边缘概率分布拟合优度检验PP图

3.3 最优联合分布函数选择

确定干旱特征变量最优边缘分布之后,需根据拟合优度检验结果从备选的4种Copula函数(包括Gumbel、Clayton、Frank、Joe)中为干旱历时-烈度组合确定最优的Copula函数用于构造联合分布。Copula函数的拟合优度检验及参数见表5。其中AIC、BIC、RMSE分别为Akaike信息准则、贝叶斯信息准则、均方根误差,指标值越小表明拟合优度检验结果越优。由表5可知,历时-烈度组合中Frank Copula的AIC、BIC和RMSE值均最小,则Frank Copula为该组合的最优联合模型。

表5 历时-烈度组合中Copula函数的拟合优度检验及参数

3.4 气象干旱联合发生概率

据干旱频率分析计算公式可知,气象干旱联合发生概率存在两种情况：一种是干旱历时或烈度中的一个变量大于等于某一特定值,简称“或”情况,例如P(D≥3∪S≥2);另一种情况是干旱历时和烈度同时大于等于某一特定值,简称“和”情况,例如P(D≥3∩S≥2)。其中，P为概率，D为干旱历时，S为干旱烈度。气象干旱特征变量的二维联合发生概率如图4所示。

图4 干旱历时和烈度的双变量干旱联合发生概率

由图4可以看出：①“或”情况下联合发生概率较高的范围比“和”情况要大的多,相同干旱特征变量组合的联合发生概率在“或”情况下比“和”情况要高,如干旱历时和烈度分别大于等于2.01个月和0.90,“或”情况下联合发生概率等于66.98%,“和”情况下联合发生概率等于29.98%。②两种情况下,联合发生概率均随着干旱特征变量的减小呈增加趋势,如“或”情况下,干旱历时和烈度分别大于等于2.31个月和0.98,联合发生概率为61.62%,干旱历时和烈度分别大于等于2.31个月和1.66,联合发生概率为39.26%;“和”情况下,干旱历时和烈度分别大于等于1.71个月和0.64,联合发生概率为39.22%,干旱历时和烈度分别大于等于2.11个月和0.64,联合发生概率为29.61%。

综上所述,联合发生概率可以定量捕捉到干旱特征变量变化条件下气象干旱的发生概率,能够为抗旱减灾及水资源管理提供重要信息。值得注意的是,如果只考虑“或”情况下的干旱联合发生概率,气象干旱风险可能会被高估,而只考虑“和”情况下的干旱联合发生概率则可能低估气象干旱风险。因此,需要对两种情况进行综合分析,以准确评估气象干旱发生概率。

4 结论

本文以贵州省为研究区,基于1960—2017年的降水、温度、风速、日照时数等气象要素计算得到该地区的SPEI来表征气象干旱情况,利用优化的游程理论识别干旱事件,采用MMK、Copula函数等方法分析贵州省气象干旱特征的时空分布规律及联合发生概率,得出以下结论:

1)贵州省近58年来长历时的严重干旱事件频繁发生,平均历时和烈度分别集中在1.8～2.3个月和4.2～13.2。贵州省东部、西南部及遵义市西北区域气象干旱具有发生频繁、持续时间短、强度弱的特点,并有干旱持续时间延长和严重程度增加的趋势。

2)贵州省近58年发生的气象干旱事件持续时间和严重程度之间具有显著的相关性,且最优边缘分布函数分别为GP分布和LogN分布;干旱历时和烈度间的最优联合模型为组Frank Copula函数。

3)相同干旱特征变量组合,在“或”情况下的联合发生概率要高于“和”情况下的,联合发生概率随着干旱特征变量的减小呈现增加趋势。

4)只考虑“或”情况，气象干旱风险会被高估,而只考虑“和”情况会低估气象干旱风险,准确合理的干旱频率分析需要对两种情况进行综合分析。