白河上游流域洪水模拟及参数敏感性分析

胡昊,李磊,王文川

(1.黄河水利职业技术学院,河南 开封 475004;2.华北水利水电大学 水资源学院,河南 郑州 450046;3.中水珠江规划勘测设计有限公司,广州 510610)

近年来,受气候变化及人类活动的影响,山洪灾害等自然灾害频发[1]。这不仅对人民的生命财产安全带来威胁,还影响社会和谐发展进程。如何准确预报山洪灾害,是水文专家及学者迫切要解决的难题。应用水文模型模拟洪水,是一种切实有效的非工程防灾手段。水文模型是通过数学物理公式来描述水文过程的高维复杂耦合函数,因此，在水文模型的构建中会存在很大的不确定性,而这种不确定性会影响模型的模拟精度和结果的准确度[2-3]。这种不确定性有一部分源自模型参数的不确定性,由于水文模型的参数较多,而不同的水文模型的参数不同,并且不是所有参数都具有实际物理含义。因此,很难做到同时提高所有参数的精度,且模型中一般也只有少数参数会对结果起到决定性作用。对于某一个特定的流域,对模型输出有重要影响以及有率定需要的参数是有限的[4]。所以要对参数的影响进行定量评估,并对参数进行敏感性分析,这样才能为模型实现更加高效的优化与率定提供支撑。

为了更好地应对山洪灾害,中国水科院提出了时空变源混合产流模型[5]。该模型本质上是一种能够在超渗、蓄满两种产流机制之间发生时空转变的水文模型。本文以白河上游流域为研究对象,利用时空变源混合产流模型对流域进行洪水模拟,运用GLUE法和Sobol法对参数敏感性进行分析,并判断流域的产流方式。此研究对于类似白河上游山丘区等中小流域开展时空变源混合产流模型参数的敏感性分析及参数选取具有一定参考价值。

1 方法介绍

1.1 时空变源混合产流模型

时空变源混合产流模型是由刘昌军等[6]提出的一种可为山洪灾害预报和预警工作提供便利的水文模型,适用于短历时、强降雨的中小流域。该模型主要包括两个方面：时空变源和混合产流。在外因(降雨入渗和蒸发)和内因(重力和基质吸力)共同作用下土壤含水量的时空变化过程称为时空变源;在土壤含水量时空变化下流域产流呈现出超渗/蓄满时空动态的组合过程称为混合产流。时空变源混合产流模型根据每一个计算时段内的水文响应单元的含水量以及累积下渗量,计算出超渗产流以及蓄满产流的面积变化,同时判别出雨强和下垫面渗流能力之间的关系,实现超渗/蓄满产流在每一个地貌水文响应单元上的时空转化。以子流域为计算单元的时空变源混合产流模型,其混合产流理论包含的产流过程有:流域蒸发、土壤蒸发、截流填洼、下渗、超渗、蓄满、优先流、壤中流、地下径流。其中，优先流是水在土壤中的某一部分的运动要快于其他部分的产流，产生这部分径流的区域称为优先流区域。混合产流成分由超渗地表产流、蓄满产流、优先流、壤中流和地下径流组成。蓄满产流由上层土壤优先蓄满得到的蓄满产流和深层土壤蓄满后向上层土壤补给产生的蓄满径流两部分组成;超渗地表产流包括不透水面积的直接超渗地表产流和透水面积在雨强大于下渗能力时的超渗产流;优先流为上层土壤出流;壤中流为下层土壤出流;地下径流为地下水出流。时空变源混合产流模型产流过程如图1所示[7]。

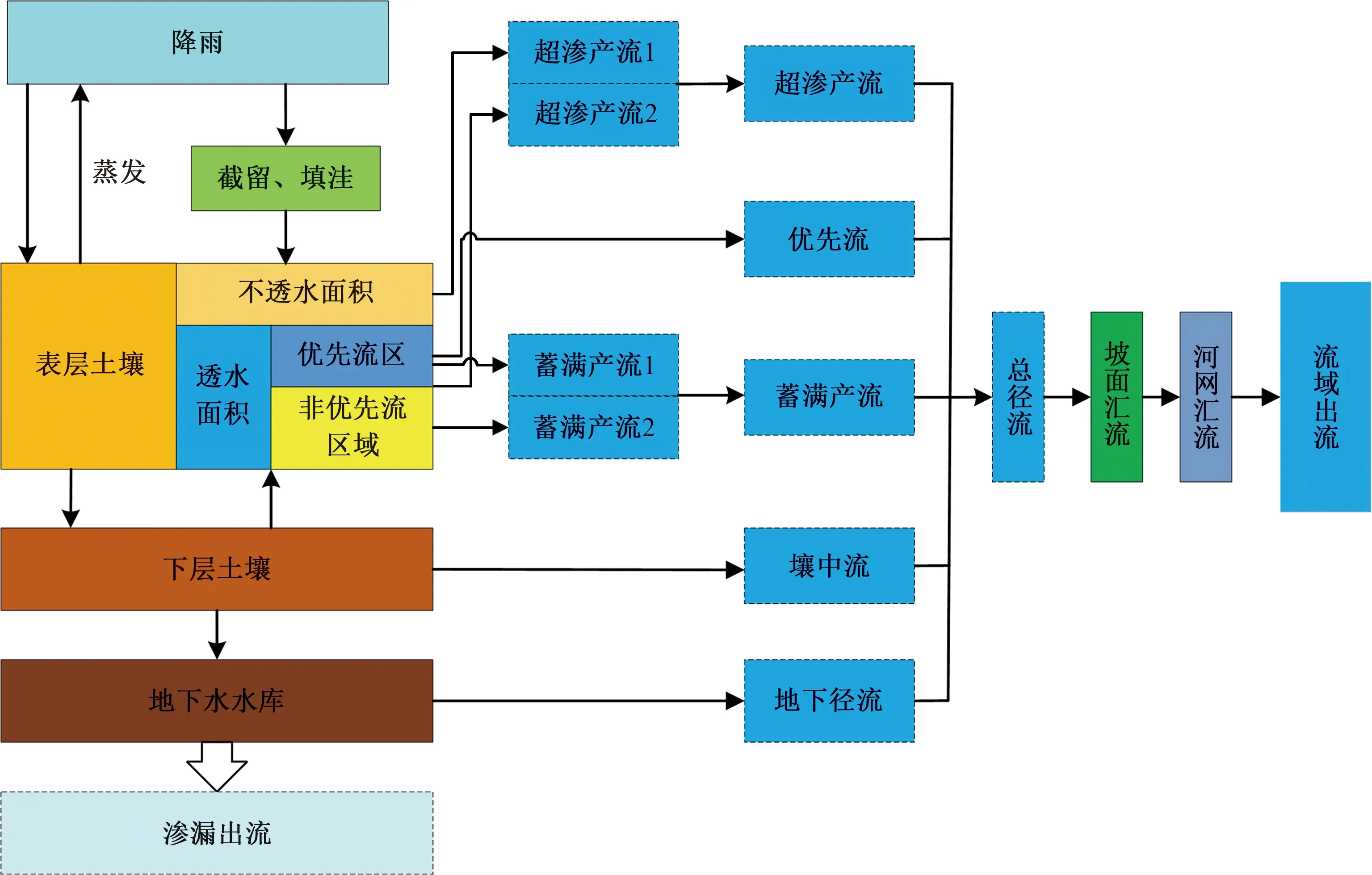
图1 时空变源混合产流过程概化示意图

时空变源混合产流模型是一种基于物理机制建立的水文模型,可分为两种计算模型:日模型与次洪模型。模型是以水文循环模块化为基础搭建的,主要有降雨以及径流两种时间序列值。模型及其相关计算的主要参数及其取值范围见表1[8]。

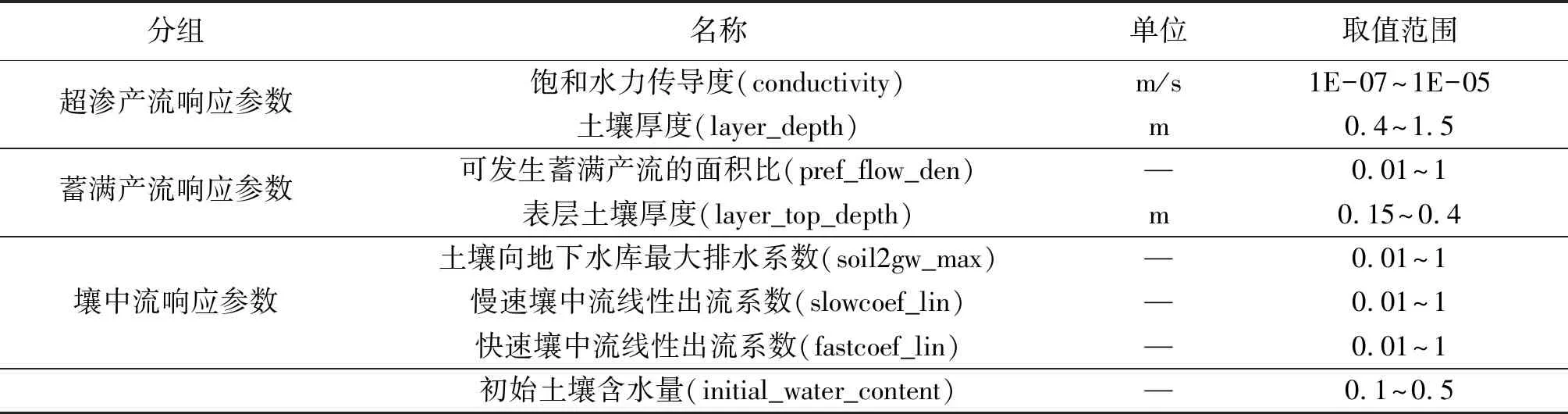
表1 时空变源混合产流模型主要产流参数及取值范围

1.2 GLUE法

普适似然函数不确定性评估(Generalized Likelihood Uncertainty Estimation,GLUE)方法[9-10],起源于区域敏感性分析(Regionalized Sensitivity Analysis,RSA)方法。水文模型的模拟性能通过多个参数的互相作用来体现,单个参数并不能完全反映水文模型的预报情况。通常,根据水文模型参数的物理意义或依据经验设定参数的取值范围,然后使用蒙特卡洛随机抽取参数组合样本,并将随机模拟参数组代入模型进行运算,根据模型模拟的洪水过程与实际洪水过程之间的似然函数值,来推求出各参数组合样本的似然值。参数敏感性是根据参数与似然值之间的分布确定的,具体步骤如下:

步骤1确定GLUE似然判据。选择反映实测洪水过程与模拟洪水过程拟合程度的确定性系数作为似然依据,计算公式为:

(1)

步骤2确定模型参数的先验分布,若不确定是哪种分布,以均匀分布表示。

步骤3根据在参数取值范围内生成的随机参数组,利用式(1)计算似然值,并绘制参数与似然值点的函数分布图。

1.3 Sobol法

Sobol法[11-12]作为一种基于方差的全局敏感性定量分析方法,能够非常有效地分析高维非线性水文模型多个变量之间相互作用的敏感性,可根据Sobol法的分析结果决定每个模型输入参数及其互相作用对整个模型输出方差的贡献度。

若用y=f(X)=f(x1,x2,…,xm)表示模型结构,x1、x2、…、xm表示模型参数(m为模型参数个数),则方差分解公式可表示为:

(2)

式中:V(y)为模型输出y的总方差;Vi为第i个参数作用下的方差项;Vij为第i个和第j个参数共同作用下的方差项;V1,2,…,m为所有参数作用下的方差项。

定义一阶敏感度Si、二阶敏感度Sij与总敏感度STi指标分别为:

(3)

(4)

(5)

式中V-i为不含第i个参数作用的方差项。一阶敏感度Si表征单一模型参数组合对模型输出的影响,二阶敏感度Sij表征两个模型参数组合对模型输出的影响,总敏感度STi刻画的是包括第i个模型参数在内的所有参数组合对于模型输出的影响。

2 实例分析

2.1 研究区概况

本次研究区域为白土岗水文站以上的白河上游流域,流域位于河南省境内,大部分面积在南阳市境内和洛阳市栾川县以及嵩县的部分地区,地理坐标为东经111°48′～112°25′、北纬33°19′～33°45′。白河上游流域地理位置如图2所示。

图2 白河上游流域地理位置图

研究区地处北亚热带北部,是南北方气候过渡地带,冬季主要受亚洲大陆强冷高压控制,寒冷高压干燥少雨,夏季主要受西太平洋副热带高压控制,西南季风活动较为频繁,温度高,雨量充沛,为河南省3个典型的暴雨中心之一,极易形成暴雨灾害。研究区年降雨量为700～1 500 mm,多年平均降雨量为891.5 mm,降雨分布不均,主要集中在汛期,其降雨量约占全年降雨量的一半以上,且暴雨频繁,经常出现洪涝,无霜期长;年平均蒸发量为892～1 244 mm,平均值为1 000 mm,蒸发的年变化与温度的年变化大致相同,通常12月至次年1月的蒸发量最小,而6—9月的蒸发量最大;河流径流和降水的变化大体相似,具有明显的季节性和区域性,同时在区域和时间上分布极不均匀。

2.2 数据来源

本文收集到的白河上游流域雨量站、水文站的数据情况见表2,雨量站与水文站的分布情况如图2所示。

表2 研究区域雨量站、水文站资料情况表

2.3 流域洪水模拟

本次收集的降雨径流资料相对齐全的年份为2012—2018年,因此截取此段时间内白河上游流域22场洪水资料,将白土岗水文站的实测径流资料以及周边雨量站的降水资料利用线性插值程序插值为逐小时流量,再运用时空变源混合产流模型进行洪水模拟,模拟误差见表3,部分洪水的模拟结果如图3所示。

表3 白河上游流域洪水模拟结果指标统计表

图3 白河上游流域部分洪水模拟结果

对挑选的22场洪水的模拟结果进行评判,将评判结果分为较好、可接受、较差3个等级。其中,较好等级的纳什系数在0.8以上,且洪峰的相对误差在10%以下;可接受等级的纳什系数为0.6～0.8,洪峰相对误差为10%～20%;较差等级的纳什系数小于0.6,洪峰相对误差大于20%。

经统计:22场洪水中,8场洪水的模拟结果为较好,10场洪水的模拟结果为可接受,4场洪水的模拟结果为较差;平均纳什系数为0.711,洪峰平均相对误差为6.80%,可接受以上等级的洪水场次占所有洪水场次的81.8%。这说明模拟的场次洪水过程与实测洪水过程具有较好的一致性,可以认为时空变源混合产流模型在由白土岗水文站控制的白河上游流域具有较好的适用性。

3 参数敏感性分析

3.1 GLUE法分析结果

在时空变源混合产流模型参数的取值范围内,运用Matlab平台编程,采用蒙特卡洛随机取样法生成2 000组随机参数组,并将其输入至时空变源混合产流模型中进行模拟,确定以反映实测洪水与模拟洪水过程重合程度的确定性系数为似然值,并绘制参数与似然值点的分布图,如图4所示。图4中,横坐标为各项参数的取值范围,纵坐标为各参数对应的似然值(纳什系数NS)。

图4 GLUE法参数敏感度示意图

从图4中可以看出,可发生蓄满产流的面积比pref_flow_den在(0,0.5)区间、表层土壤厚度layer_top_depth在(0,0.2)区间、快速壤中流线性出流系数fastcoef_lin在(0,0.3)区间、初始土壤含水量initial_water_content在整个区间都有明显的变化,说明这4个参数在各自划定的取值范围内非常敏感;而饱和水力传导度conductivity、土壤厚度layer_depth、土壤向地下水库最大排水系数soil2gw_max、慢速壤中流线性出流系数slowcoef_lin变化不明显,说明取值范围内的参数组对洪水模拟影响并不大。由此,可以判断出本次研究的敏感参数有pref_flow_den、layer_top_depth、fastcoef_lin、initial_water_content;非敏感参数有conductivity、layer_depth、soil2gw_max、slowcoef_lin。

3.2 Sobol法分析结果

同GLUE法,在时空变源混合产流模型的参数取值范围内,使用蒙特卡洛随机抽样法,生成2 000组随机参数组合,将其分别输入至时空变源混合产流模型中,根据确定性系数来计算总敏感度STi(式(3)),选取敏感度大于0.01的参数为主要敏感参数,计算结果如图5所示。由图5可知:fastcoef_lin、pref_flow_den、layer_top_depth、slowcoef_lin、initial_water_content、soil2gw_max为敏感参数,其总敏感度分别为0.565、0.524、0.493、0.080、0.044、0.011,敏感度占比分别是33%、30%、29%、5%、2%、1%;非敏感参数为conductivity、layer_depth。

图5 Sobol法参数敏感性分析图

3.3 参数敏感性结果分析

根据GLUE法和Sobol法对应的参数敏感性分析结果,可以判断在白河上游流域,模型参数fastcoef_lin、pref_flow_den、layer_top_depth、initial_water_content为主要敏感参数,其数值变动对结果有较大影响。由此说明:由白土岗水文站控制的白河上游流域的产流方式符合蓄满产流机制,可划归为湿润地区,其主要径流成分是蓄满产流和壤中流,其次是地下径流,超渗产流的比例最小,土壤特征对洪水过程影响显著。

4 结论

本文以白河上游流域作为研究区域,运用时空变源混合产流模型模拟了研究区2012—2018年间的22场洪水,并采用GLUE法和Sobol法对模型参数的敏感性进行了分析。得到如下结论:

1)22场洪水的平均纳什系数为0.711,洪峰平均相对误差为6.80%,可接受以上标准的洪水场次占所有洪水场次的81.8%,模拟场次洪水过程与实测洪水过程吻合较好,说明用时空变源混合产流模型分析白河上游流域时具有较好的适用性。

2)使用GLUE法得出的敏感参数有pref_flow_den、layer_top_depth、fastcoef_lin、initial_water_content;使用Sobol法得出的敏感参数为astcoef_lin、pref_flow_den、layer_top_depth、slowcoef_lin、initial_water_content、soil2gw_max。结合实际计算过程和两种参数敏感性方法分析结果认为，白河上游流域的敏感参数为fastcoef_lin、pref_flow_den、layer_top_depth、initial_water_content。

3)白河上游流域以蓄满产流方式为主。