基于TSA-DRNN模型的年径流预测研究

崔东文，杨琼波

(1.云南省文山州水务局，云南 文山 663000；2.云南省水文水资源局 红河分局，云南 红河 661100)

由于受气候、气温、人类活动等大量不确定性和复杂性因素的影响，径流序列表现出高度非线性、时变、不确定等特性，常规回归分析、数理统计等方法很难获得理想的预测效果。目前，探索具有更高径流预测精度的模型及方法仍是水文预测预报研究中一项具有挑战性的工作。近年来，人工神经网络[1-4]、支持向量机[5-7]、随机森林[8-9]、极限学习机[10]、自适应神经模糊系统[11]、耦合模型[12]等智能化模型及方法被广泛应用于径流预测，并获得了较好的预测效果。Elman神经网络为典型的局部递归网络，具有较强的动态信息处理能力[13]，在径流预测中有着广泛的应用[14-15]。然而，在实际应用中，Elman神经网络存在以下不足：①Elman网络学习过程与BP等前馈神经网络相类似，存在收敛速度慢和易陷入局部极值等问题。目前，遗传算法[14]、粒子群优化算法[16]、人工鱼群算法[17]、果蝇优化算法[18]等常用于Elman初始权值和阈值的优化，使Elman预测效果得以改善。②Elman神经网络只有一个隐含层，结构单一，对于复杂问题预测精度不高，效果不理想。深度递归神经网络(Deep Recurrent Neural Network，DRNN)类似于多隐层(两个及以上隐含层)Elman神经网络，具有多隐层结构，不但能够刻画和描述复杂的高维、非线性系统，而且具备动态反馈机制，能全面刻画与表征动态序列的内在规律，具有较好的应用前景[19]。不足之处在于DRNN初始权值和阈值难以确定，这在很大程度上影响和制约着DRNN模型预测性能的提高。

为了有效提高DRNN模型预测精度和解决DRNN权值和阈值优化问题，本文提出一种基于被囊群算法(Tunicate Swarm Algorithm，TSA)与DRNN相融合的径流预测方法。首先，简要介绍TSA算法，并通过4个标准测试函数对TSA进行仿真验证；其次，采用主成分分析(PCA)对径流序列进行降维处理，并通过降维数据构建DRNN2(双隐层DRNN)、DRNN3(三隐层DRNN)、DRNN4(四隐层DRNN)，利用TSA优化DRNN2、DRNN3、DRNN4的权值和阈值，建立TSA-DRNN2、TSA-DRNN3、TSA-DRNN4径流预测模型，并构建TSA-Elman、Elman、DRNN2、DRNN3、DRNN4、TSA-SVM模型作对比；最后，将所建立的TSA-DRNN2、TSA-DRNN3、TSA-DRNN4、TSA-Elman、Elman、DRNN2、DRNN3、DRNN4、TSA-SVM模型应用于云南省姑老河站年径流预测实例中，旨在验证TSA-DRNN模型用于径流预测的可行性，并为DRNN权值和阈值的优化研究提供参考。

1 TSA-DRNN预测模型的建立

1.1 被囊群算法(TSA)

1.1.1 TSA描述

被囊动物是网状小型生物，遍布于海中。因覆盖在身体上坚韧纤维状皮膜而得名，它们过着独居或寄居的生活，有能力在海洋中找到食物来源位置。被囊群算法(TSA)是Satnam Kaur等[20]于2020年提出的一种新型生物启发式优化算法，其灵感就来源于海洋中被囊射流推进迁移和群体智能觅食行为。参考文献[20]，TSA简述如下：

(1)

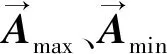
(2)

(3)

(4)

3)向最好被囊方向移动。在避免了被囊间的冲突后，被囊向着最佳邻居(被囊)方向移动，数学描述如下：

(5)

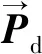
4)趋近最佳邻居(被囊)。被囊向最佳邻居(被囊)位置移动的数学描述如下：

(6)

5)被囊群行为。为了在数学上模拟被囊的群体行为，TSA通过保存前两个最优解，并根据最佳被囊位置更新其他被囊位置来实现。被囊群体行为数学描述如下：

(7)

1.1.2 TSA仿真验证

选取Sphere、Schwefel 2.22、Griewank、Ackley 4个典型测试函数在不同维度条件下对TSA进行仿真验证，并与PSO(粒子群优化)算法的仿真结果进行比较。其中，单峰函数用于评测TSA的寻优精度，多峰函数用于评测TSA的全局搜索能力，并通过TSA 20次寻优平均值进行性能评估，结果见表1。试验参数设置为：TSA、PSO算法最大迭代次数T=1 000，种群规模N=100。其中，TSA社交互动初始速度和辅助速度Pmin、Pmax分别设置为1和2。PSO算法自我学习因子c1、社会学习因子c2均取值2.0，惯性权重wmax、wmin分别取值0.9和0.6。

表1 函数优化对比结果

从表1中可以看出，无论是单峰函数还是多峰函数，TSA在不同维度条件下寻优精度均远优于PSO算法，具有较好的寻优精度和全局搜索能力。

1.2 深度递归神经网络(DRNN)

递归神经网络(Elman神经网络)按结构可分为单隐层Elman神经网络和深度递归神经网络(DRNN)。理论上，单隐层Elman神经网络已能映射或逼近任何有理函数，但对于复杂问题，单隐层Elman神经网络存在预测精度低和泛化能力弱等问题。同单隐层Elman神经网络相比，DRNN通过承接层存储前一时刻隐含层神经元的输出值并将其返回给第1隐含层的输入，使网络最终的输出不仅与当前时刻信息有关，而且与每一时刻的历史信息也密切相关，具有较强的动态信息处理能力，不但预测精度高、泛化能力强，而且易避免网络训练陷入局部最优[19]。

设DRNN输入向量为X=[x1，x2，…，xm]，有n个隐含层，每层节点数分别用l1、l2、…、ln表示，输出层节点个数为1，则DRNN数学描述如下[19]。

DRNN第1隐含层在t时刻的输出向量可表示为：

R1(t)=f{W1[X(t),z(t)]+B1}。

(8)

式中：R1(t)为第1隐含层输出；W1、B1分别为输入层与第1隐含层之间的权、阈值矩阵；f为DRNN隐含层传递函数；z(t)为反馈状态向量。

DRNN在t时刻除第1层外的其他隐含层的各层输出可描述为：

RL(t)=f{WLRL-1(t)+BL}。

(9)

式中：RL(t)为第L隐含层的输出向量；WL、BL分别为第L-1隐含层与第L隐含层之间的权、阈值矩阵。

DRNN在t时刻输出层的输出y(t)可描述为：

y(t)=g[Wn+1Rn(t)+Bn+1]。

(10)

式中：Wn+1、Bn+1分别为第n+1隐含层与输出层之间的权、阈值矩阵；g为DRNN输出层传递函数。

1.3 预测模型的建立及实现步骤

TSA优化DRNN权值阈值的基本思想为：将DRNN权值和阈值映射为TSA中各被囊个体空间位置矩阵，设计TSA-DRNN模型适应度函数，将TSA-DRNN模型最优问题转化为求解适应度函数全局最小时对应的被囊个体，该被囊个体位置即为全局最优解，根据被囊个体空间位置与DRNN权值、阈值映射关系，即可得到DRNN最优权值、阈值[21]。具体实现步骤如下：

步骤1采用PCA对实例数据进行降维，划分训练、预测样本。确定DRNN结构，并构建DRNN2、DRNN3、DRNN4模型，利用TSA优化DRNN2、DRNN3、DRNN4权值和阈值，建立TSA-DRNN2、TSA-DRNN3、TSA-DRNN4径流预测模型，利用训练样本数据对TSA-DRNN2、TSA-DRNN3、TSA-DRNN4模型进行训练。

PCA降维基本思想是用一组维数较少且不相关的综合变量F1、F2、…、Fm来代替原来维数较多且有一定相关性的变量X1、X2、…、Xn(m≤n)[22-23]，见下式：

(11)

步骤2选用训练样本均方误差作为优化目标函数，描述如下：

(12)

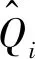
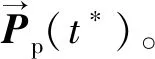
步骤5利用公式(7)更新被囊位置。

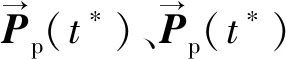
2 实例分析

2.1 数据来源及分析

姑老河站位于南汀河干流下游，系南汀河干流控制站，控制径流面积4 186 km2，为国家重要水文站。南汀河发源于临沧市临翔区博尚镇永泉村，国境内径流面积8 097 km2，河长264 km，落差2 090 m，平均比降4‰，流域内河网水系发育较差，河网密度0.4，流域形状系数0.16，主要支流有南捧河、西河、盘河、河底岗河等。本文以云南省姑老河站年径流为预测对象，采用SPSS数据分析软件计算姑老河站1月至10月的月径流与相应年份年径流的相关系数。经计算，相关系数为0.266～0.780，二者相关性并不十分显著。

依据式(11)对1月至10月的月径流进行降维，经降维，发现前6个特征值累计贡献率达89.409%，大于85%，可认为此6个特征变量代表了原月径流大部分信息，故选取前6个变量代替原10个变量进行年径流预测。分别选取1960—2003年、2004—2013年实测数据作为训练样本和预测样本。降维后的数据统计结果见表2(表中Q为实测径流量)，原始数据限于篇幅从略。

表2 实例径流降维后数据统计结果

2.2 参数设置

为客观、公平地比较各模型的预测效果，TSA-DRNN2等模型的参数设置见表3。各模型均采用[-1,1]对数据序列进行归一化处理。

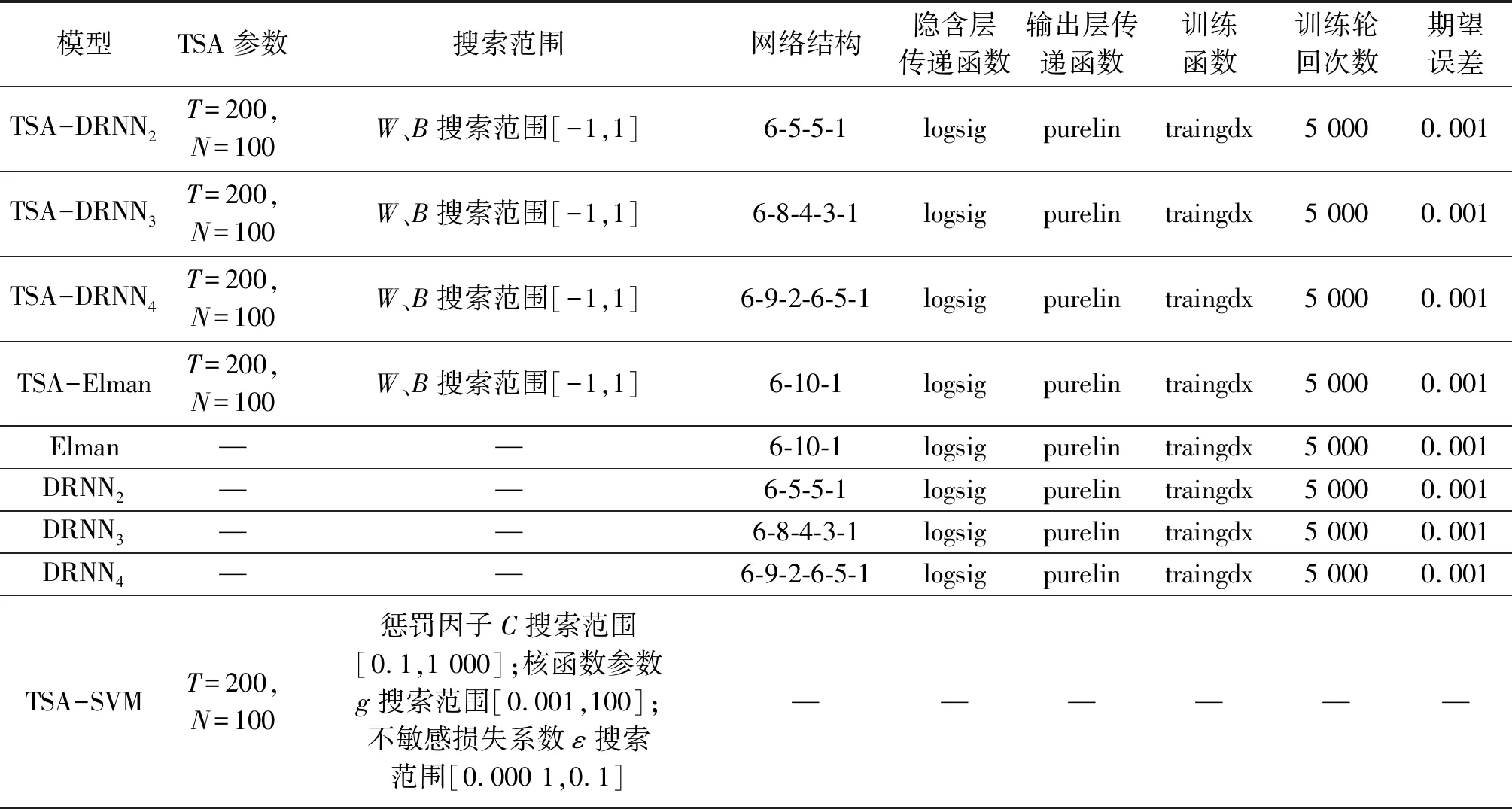
表3 各模型参数设置统计表

2.3 预测及对比分析

利用所构建的TSA-DRNN2、TSA-DRNN3、TSA-DRNN4、TSA-Elman、Elman、DRNN2、DRNN3、DRNN4、TSA-SVM模型对实例年径流进行训练及预测，利用平均相对误差MAPE(%)、平均绝对误差MAE(m3/s)对各模型预测性能进行评价。拟合、预测结果见表4,拟合-预测误差如图1、图2所示。

表4 不同模型年径流测结果及对比

(13)

依据表4及图1、图2可以得出：

1)TSA-DRNN2、TSA-DRNN3、TSA-DRNN4模型对实例年径流预测的MAPE分别为3.63%、2.81%、2.50%，MAE分别为2.57、2.52、2.18 m3/s，预测精度优于TSA-Elman、Elman、DRNN2、DRNN3、DRNN4、TSA-SVM模型的，表明TSA能有效优化DRNN权值和阈值，具有更高的预测精度和更强的泛化能力，尤以TSA-DRNN4模型的拟合、预测效果最好。因此，将TSA-DRNN模型用于径流预测是可行的。

2)从具有相同网络结构和参数设置的TSA-DRNN2与DRNN2模型、TSA-DRNN3与DRNN3模型、TSA-DRNN4与DRNN4模型的预测结果对比来看，TSA-DRNN2、TSA-DRNN3、TSA-DRNN4模型预测的相对误差较相对应的DRNN2、DRNN3、DRNN4模型的分别降低了47.8%、59.0%、43.7%，绝对误差较相对应的DRNN2、DRNN3、DRNN4模型的分别降低了57.0%、55.6%、39.8%。这表明TSA能有效优化DRNN权值和阈值，大大提高DRNN模型预测精度，而且随着隐含层数的增加，预测精度呈提高趋势。TSA-DRNN模型用于径流预测是可靠的。

3)从图1、图2可以明显看出，TSA-DRNN模型具有较好的拟合、预测效果，其预测的相对误差、绝对误差分别在-10.1%～7.75%、-6.84～7.33 m3/s范围内波动，与其余6种预测模型相比，其稳定性和预测精度均较高。

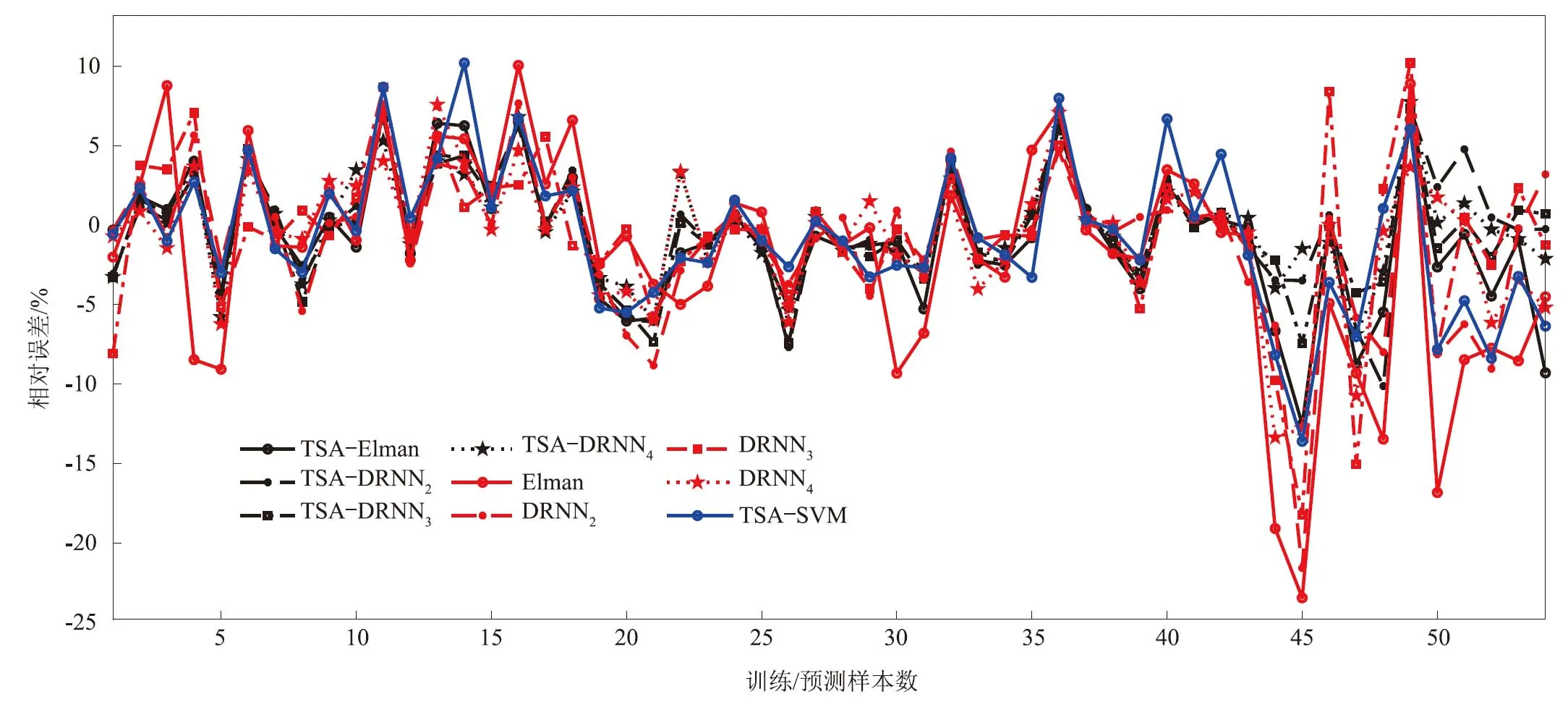
图1 拟合-预测相对误差图

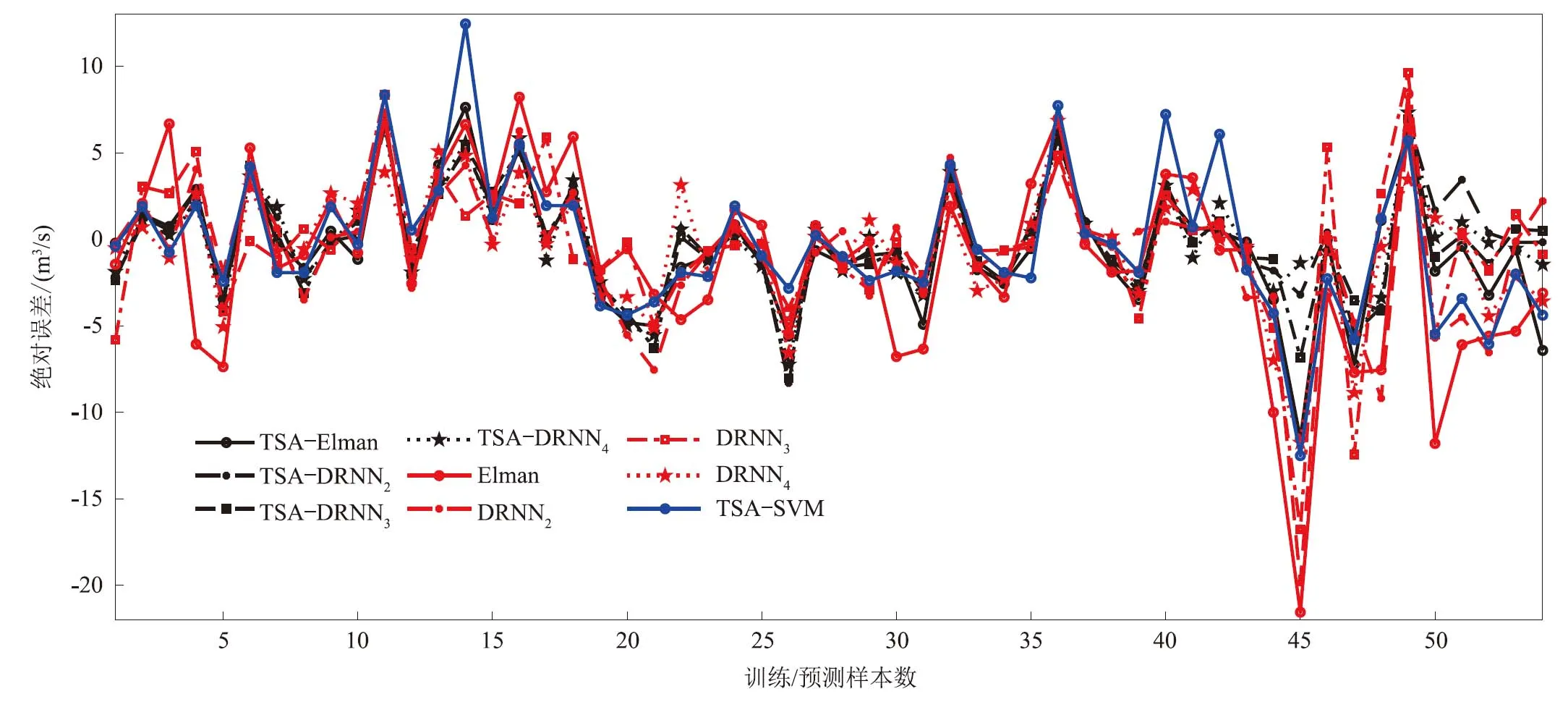
图2 拟合-预测绝对误差图

4)对于该实例，TSA-DRNN模型的预测效果优于TSA-Elman、DRNN4、DRNN2、DRNN3、TSA-SVM模型，远优于Elman模型。

3 结论

为解决DRNN权值和阈值优化问题，有效提高DRNN预测精度，本文提出了TSA与DRNN相融合的TSA-DRNN径流预测模型，利用云南省姑老河站年径流预测实例对TSA-DRNN2(双隐含层)、TSA-DRNN3(三隐含层)、TSA-DRNN4(四隐含层)模型进行检验，并构建TSA-Elman、Elman、DRNN2、DRNN3、DRNN4、TSA-SVM模型作对比，得出以下结论：

1)通过4个标准测试函数对被囊群算法(TSA)进行仿真验证，并与粒子群优化(PSO)算法的仿真结果进行比较，证明了TSA在不同维度条件下具有较好的寻优精度和全局搜索能力，将TSA用于DRNN权值、阈值寻优是可靠的。

2)TSA-DRNN2、TSA-DRNN3、TSA-DRNN4模型对实例年径流的预测精度优于TSA-Elman等其他6种模型，具有更好的预测精度和更强的泛化能力，表明TSA对DRNN权值和阈值具有较好的优化效果，将TSA-DRNN模型用于径流预测是可行的，尤以TSA-DRNN4模型的拟合、预测精度最高。

3)从具有相同结构和参数设置的TSA-DRNN2与DRNN2模型、TSA-DRNN3与DRNN3模型、TSA-DRNN4与DRNN4模型的预测结果对比来看，通过TSA优化DRNN权值和阈值，有效改善了DRNN模型的预测效果，随着隐含层数的增加，预测精度呈提高趋势。模型及优化方法可为相关预测研究和DRNN权、阈值优化提供借鉴。