三种重力场垂向分离方法对比试验研究

索奎，彭少飞，刘爱涛，赵贵章

(1.华北水利水电大学 地球科学与工程学院，河南 郑州 450046；2.北京华宇工程有限公司，北京 100120；3.河北省地质调查院，河北 石家庄 050081)

重力勘探是重要的地球物理勘探方法之一，重力异常是不同深度、不同尺度的地质体产生的重力异常叠加的结果。当研究某个地质体时，需要将目标地质体产生的重力异常从总场中分离出来，这是进行数据处理、三维反演及解释的前提。重力数据的分离问题一直没有彻底解决，尤其是垂向分离效果不佳，这是因为二维重力数据不包含垂向信息，影响了重力数据处理、解释的精度及可靠性，在一定程度上限制了重力勘探的应用范围。

有多种方法能够实现重力场垂向分离，常用的有趋势分析[1]、垂向导数、插值切割[2]、解析延拓[3]和匹配滤波[4]等方法，分别在不同的应用条件下取得了一定的效果。多数方法分离的结果受主观因素影响较大，这是因为各种参数对结果影响较大且没有客观标准。ALBORA A M等[5]和OSMAN A等[6]将神经网络算法引入到重力场和磁场的分离中；ALBORA A M和UCAN A[7]采用差分马尔可夫随机场方法进行重力场分离，获得了较好效果；陈召曦[8]利用曲波变换实现了局域场与区域场的分解，并指出曲波变换在一定程度上能够更好地反映地质细节；葛粲等[9]提出了动态改进型插值切割算子，得到了更好的分离效果。近年来，随着小波变换技术的快速发展，利用小波多尺度分析法进行位场垂向分离得到了广泛应用[10-13]，该方法利用了小波分解的低阶不变性，不会使原始数据失真，不同分解阶数反映了不同深度的位场信息；LI Y和OLDENBURG D W[14]利用三维反演方法实现了磁区域场和局部场的分离，该方法避免了数据网格化过程，获得了较好的应用效果。

以上方法针对不同的应用条件，选用不同的参数组合，均能基本实现重力场的垂向分离。但由于重力场体效应的原因，以及各个方法在应用中的局限性，通常很难将浅源场(局部场)和深源场(区域场)完全分离开来。本文通过模型试验和实际数据处理，对比匹配滤波、小波多尺度分析和反演分离3种方法的重力场垂向分离效果，为实际应用中的参数选择、效果评估提供参考。首先，建立一个中源和深源为层状构造、浅源为数个三度体的组合模型，以其正演重力场作为观测值，分别采用3种方法对观测值进行分离，并将3个深度上的分离重力场分别与组合模型的浅、中、深理论重力异常场进行定量比较，以研究3种分离方法的模型试验效果。其次，对实际地区数据进行处理，综合分析分离结果的实际应用效果，对比研究3种方法的优缺点。

1 重力场分离方法

重力场分离的方法有多种，匹配滤波法在频率域实现了重力场的分离，是经典的分离方法之一；小波多尺度分析法是近年来迅速发展起来的小波域重力场分离方法；反演分离法则利用三维反演在空间域实现了重力场的分离。这3种方法分别代表了不同的实现场分离的思想，因此本文选择这3种具有代表性的方法进行对比研究。

1.1 匹配滤波法

一般深部地质体的重力异常特征较为平缓，因此区域场在频率域中以低频成分为主，而浅部地质体的异常特征变化较为剧烈，局部场在频率域中以中高频成分为主，这是利用匹配滤波法对其进行分离的基础。SPECTOR A等[4]设计了匹配滤波器用来分离不同深度的异常，并且经过改善后，该法得到了进一步发展。匹配滤波器是一个计算输入信号自相关函数的相关线性滤波器，其输出信号瞬时功率与噪声平均功率的比值最大。当提取局部场时，匹配滤波器是一种高通滤波器；提取区域场时，其则是一种低通滤波器。

对于重力异常，先求取垂向一阶导数，再计算其径向平均对数功率谱，根据功率谱曲线求取参数，最后进行匹配滤波计算，达到场垂向分离的目的。当局部场和区域场的波数成分重叠较少，又能选择准确的滤波参数，则会取得较好效果，因此仔细分析功率谱曲线是获得良好分离效果的基础。与其他频率域分离方法不同的是，匹配滤波方法中进行场分离的截止频率并非人为给定，而是用直线分别拟合功率谱曲线的高频段和低频段，拟合误差影响了截止频率的确定，从而在一定程度上影响了分离结果的准确性。

1.2 小波多尺度分析法

小波多尺度分析是把空间分解为一系列不同尺度的子空间的过程，可以将原函数分别投影在不同尺度的子空间中，因而能够实现在不同尺度对原函数进行分析的目的。对总场进行小波多尺度分析后，可以将总场分解为不同尺度的异常，一般小尺度异常表示局部异常，大尺度异常反映的是区域异常，由此可以实现局部场和区域场的分离。

通常，实际测得的重力异常数据为二维信号，用函数f(x,y)表示，x、y分别表示横、纵坐标。设f(x,y)为L2(R2)二维实空间内的二维函数，二维小波尺度函数可以分解为：

φ(x,y)=φ(x)·φ(y)。

(1)

小波函数可以分解为：

(2)

(3)

式中j为分解尺度。

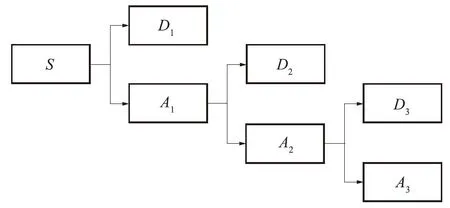
S—原始信号；D—高频细节部分；A—低频逼近部分图1 小波三层多分辨率分析示意图

因此，对于重力数据，也可以通过小波多尺度分析将总场分解为局部场和区域场，n阶分解的表达式为：

(4)

利用小波多尺度分析方法进行重力场分离同样存在问题。一是小波基函数多种多样，并非所有基函数都适合进行重力场分离。基于重力场的特性，分解后的局部场和区域场之和应等于总场，因此需要选择正交小波来进行重力场的分离，常用的正交小波族包括DB、SYM和COIF等。选择不同的基函数能够获得不同的结果，如何确定小波基函数依赖主观判断。二是利用该方法分离的局部场无法直接确定其场源深度，一般利用平均对数功率谱曲线计算场源埋深，受曲线划分、拟合误差等因素影响，结果不够精确。

1.3 反演分离法

前两种方法主要是利用局部场和区域场的不同异常特征来进行场分离，随着重力三维反演算法的不断进步，使得计算速度更快，反演结果更可靠，为重力场垂向分离提供了一种新思路[14]，基本原理如下。

假设有地下场源区域(称为“源区”)A和B，其引起的重力场分别为gA和gB，设二者之和为gC，有gC=gA+gB，C为A、B区域之和，如图2所示。重力场分离的目的是从gC中分离出gA和gB。首先利用实测重力场gC进行三维反演，获得C的地下密度分布，此时将A区域内的密度差设为0 g/cm3，等效于“抠除”了A区域“地质体”，仅剩B区域的“地质体”，然后对B区域进行正演计算，得到重力场为gB，此时有

图2 地下场源区域相对位置示意图

gA=gC-gB，

(5)

则gA即为源区A的重力场。

该方法的优势在于计算局部场准确，可以根据需求定义目标源区A的范围和深度，能够去除目标源区A周围异常体的影响，适合为精细的三维重力反演提供剩余重力场数据。缺点是：由于重力反演上漂现象的存在，选择目标源区的垂向范围需要多次试验对比确定；此外由于反演需要的数据范围较大，加上三维反演计算速度限制，耗时与普通方法相比较长，但仍不失为一种具有良好应用前景的重力场垂向分离方法。

2 理论模型试验

通过理论模型试验对比研究匹配滤波法、小波多尺度分析法与反演分离法的重力场分离效果。

建立一个包含6个块体的组合模型，各个模型块体位置及编号如图3所示，块体参数见表1。地下场源区域范围：东西向0～400 km、南北向0～300 km、垂向0～130 km。为了给反演分离法提供更大范围的数据，地表测网水平方向各向外扩展了24 km，正演计算得到了2 km×2 km网格的重力场作为观测场。地下模型主要分为3层：0～14 km为浅层，有4个形态不同、密度有正有负的异常体；28～70 km是中间层，上界面有一个高度为12 km的半椭球凸起，剩余密度为0.1 g/cm3；70～130 km是深层,上界面有一个深度为15 km的半椭球凹陷，剩余密度为-0.2 g/cm3。

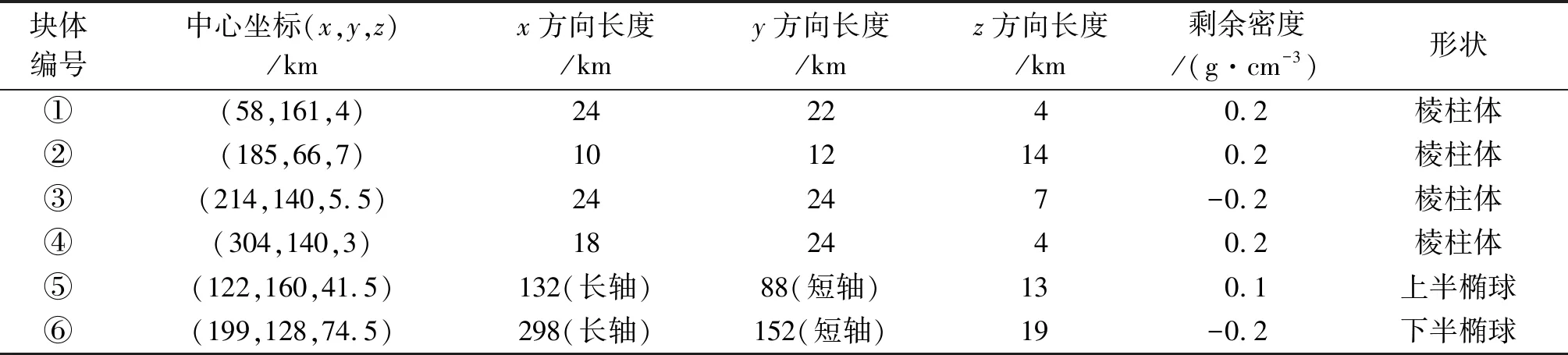
表1 组合模型块体参数表

对组合模型(图3(a)、图3(b))进行正演计算得到重力场(图3(c))，其中图3(c)为所有地质体正演计算得到的总场，它将作为模型试验的观测异常值。

从组合模型正演得到的总场(图3(c))可以看到，反映浅部模型的4个小异常与模型轮廓相符，反映中、深部模型密度异常的区域场为椭圆形。总体上看：浅源场较为明显，使得分离相对容易；中源场密度为正值，但幅值较小，在总场中基本被深源场密度负异常淹没，难以进行分离；深源场的密度负异常较明显，但仍难以与中源场分离开来。接下来分别利用3种方法对浅、中、深源场进行分离，并对比分离结果。为了便于比较，统一相同层位分离结果的色标。3种方法分离重力场的结果如图4所示，其中图4(a)、图4(b)和图4(c)分别是对浅、中、深3个深度上的地质体进行正演计算获得的浅源场、中源场和深源场，作为理论值与分离结果进行对比。

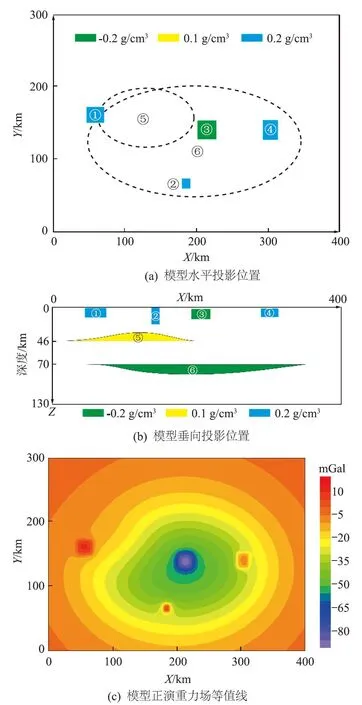
图3 组合模型正演结果

2.1 匹配滤波法分离结果

使用匹配滤波进行重力场分离，需要根据重力场一阶垂向导数的径向平均对数功率谱曲线求得滤波因子，其中绘制拟合直线受到人为主观因素影响，得到的参数存在误差。本次试验为了求得更准确的结果，直接利用已知参数进行匹配滤波计算，去除了人为因素的影响，确保了匹配滤波法的分离效果，浅、中、深源计算结果如图4(d)、图4(e)、图4(f)所示，均方根误差见表2。

图4 3种方法分离重力场结果

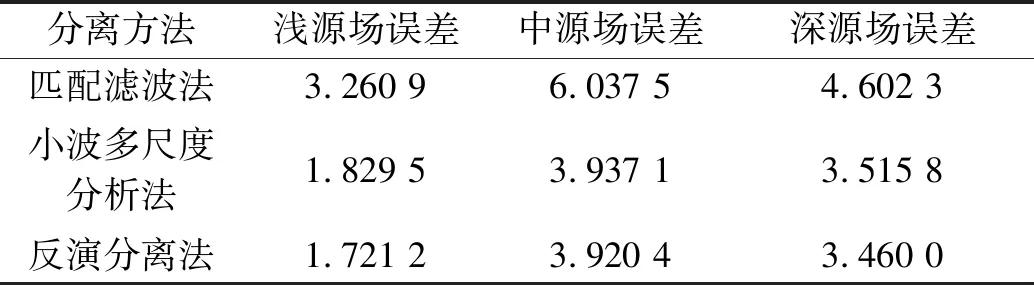
表2 3种方法分离重力场均方根误差 mGal

从图4(d)、图4(e)、图4(f)中可以看出：浅源场能够清晰地圈定①—④号模型块体的位置和形态，但由于受到了中、深源场的影响，浅源场误差较大，均方根误差达到了3.260 9 mGal，是3种方法计算结果中误差最大的，且显示理论值为负值的③号模型块体为正异常；中源场结果仍受到浅源场的影响，与理论值(图4(b))形态相比差别较大，无法辨别出中源场的形态，误差达到了6.037 5 mGal，且存在大量负值区域，与理论值不符；深源场形态与理论值(图4(c))类似，但仍受到了⑤号模型块体凸起引起的中源场的影响，误差达到了4.602 3 mGal。总体看来，匹配滤波对该组合模型的中、深源场分离结果不是很理想。

2.2 小波多尺度分析法分离结果

利用小波多尺度分析法进行重力场分离的流程是先选定合适的小波基，确定分解层数，将总场分解为多层信号，然后对每一层的信号进行重构，实现对总场的分离，其中选择合适的小波基十分关键，将直接影响到分离结果。根据李红雨等[15]的研究结论，本次试验分别选择了DB、SYM和COIF小波族进行了分解，根据分离结果最终确定COIF3作为小波基，利用6层分解分别得到了浅、中、深源场的分离结果，如图4(g)、图4(h)、图4(i)所示，均方根误差见表2。

从图4(g)、图4(h)、图4(i)中可以看出：分离得到的浅源场较为理想，①—④号模型块体的轮廓清晰，数值范围较准确，均方根误差为1.829 5 mGal，比匹配滤波结果的误差小很多；中源场形态与理论值相差很大，最高值区域与①号模型块体位置基本重叠，③号模型块体引起的负异常和深源场共同影响了中源场的形态，使得中部存在较大范围的负值区域，其误差为3.937 1 mGal，低于匹配滤波结果；深源场形态与理论值类似，误差小于匹配滤波结果，为3.515 8 mGal。总体来说，小波多尺度分析法分离结果优于匹配滤波结果。

2.3 反演分离法分离结果

利用反演分离法进行重力场分离，首先要对扩边后的区域进行三维反演，坐标范围为x(东西向)：-24～424 km；y(南北向)：-24～324 km；z(垂向)：0～130 km。地表观测数据的分辨率为2 km×2 km，为了减少反演耗时，在此次三维反演中地下网格剖分间隔大于地表观测数据间隔。设定研究区域反演剖分网格x方向长度为8 km，y方向长度为6 km，z方向长度为2 km。反演参数设定剩余密度区间为-0.5～0.5 g/cm3，没有参考模型。计算得到结果后，将浅源范围(x：0～400 km；y：0～300 km；z：0～15 km)内所有单元体密度值设为0 g/cm3，作为新的模型。正演该模型得到结果后，用观测场减去正演结果，得到浅源场。采用类似方法同样可以分别计算得到中源场和深源场，浅、中、深源场的计算结果如图4(j)、图4(k)、图4(l)所示，均方根误差见表2。

与前两种方法分离得到的浅、中、深源3种场的结果相比，从图4(d)、图4(g)和图4(j)中可以看出：反演分离法分离的浅源场效果较好，在4个模型块体周围有一个较大范围的低值正异常，其余位置与理论值基本无差别，异常数值准确，与理论值误差也最小，仅为1.721 2 mGal；中源场受到了浅源场和深源场的影响，尤其是中部存在部分负值区域，但与前两种方法分离得到的中源场相比，负值范围较小，数值区间与理论值最为接近，误差为3.920 4 mGal，优于前两种方法得到的结果；深源场形态与理论值略有差异，但形态基本一致，与前两种方法相比误差最小，为3.460 0 mGal。总体来看，反演分离法是3种方法中对该组合模型分离效果相对最好的。

3 实际数据处理

以某区域1∶20万实测布格重力异常数据(图5(a))为例，B区域东西长609 km，南北长390 km，布格重力异常范围为-473～-574 mGal，试图从中提取反映A(东西150～450 km，南北100～300 km)区域0～40 km深度范围内的浅源重力场，为进一步的数据处理做准备。分别采用了匹配滤波法、小波多尺度分析法和反演分离法对布格重力异常进行处理，其中小波分解采用了DB4小波5阶分解，得到的结果分别如图5(b)、图5(c)和图5(d)所示。

图5 某区域布格重力异常及用3种方法得到的浅源重力场分离结果

对比图5(b)、图5(c)和图5(d)可以发现，3种分离方法得到的浅源场结果基本形态类似，但场值变化范围分别是40、48、58 mGal，差异较大。其中，小波多尺度分析法和反演分离法得到的场值范围相近，而匹配滤波法结果的细节信息损失相对较多。由前述组合模型试验(与此次实际地区类似结构)可知：匹配滤波法分离结果的场值范围相较于其他两种方法的准确度较低，且此次得到的浅源场值均为负值，与实际情况不相符；小波多尺度分析结果与反演分离结果相比缺少了部分正异常细节信息，这从场源范围中可以看出，而且在区域边缘位置差异较大，以东北角、东南角差异最为明显。根据前文试验结果可知，该差异是由A区域周围密度异常体的影响引起的。经过进一步的三维反演证实(另文)，反演分离法的分离结果与目前已知的信息吻合较好。从实际地区数据处理结果来看，反演分离法较另两种方法得到的浅源场更准确。

4 结果与讨论

1)模型试验结果(图4、表2)和实际数据处理结果(图5)表明：反演分离法与匹配滤波法、小波多尺度分析法相比，从分离结果的形态、数据范围和误差来看，效果都更为理想。其主要原因是反演分离法能够计算出感兴趣的任意目标体异常场，同时排除周围区域的密度异常体影响，这是目前其他场分离方法无法做到的，这种仅反映目标区域的异常也是最适合进行三维反演的。在本次模型试验中，如果能添加部分先验信息，进一步加密反演网格，会取得更好的分离效果。

反演分离法存在部分问题：一是要求数据范围较大，对于没有大范围数据的情况，仅能保证中间位置场的分离效果；二是由于计算速度和数据分辨率的限制，反演网格剖分不能太密，这也是该方法仍存在误差的原因之一；三是随着深度的加深，反演结果的误差也越大，这是在实际数据处理中需要考虑的问题。

2)匹配滤波法进行重力场垂向分离的参数选取容易被主观因素影响，通常导致不同操作者的分离结果有较明显差异。本次模型试验是在已知匹配滤波参数的情况下得到的分离结果，与其他两种方法相比误差较大，可能是因为中、深部场源频谱重叠区域较大，如果利用能谱曲线求得的参数进行计算，误差可能会更大。对于较为明显的浅源异常，匹配滤波法能够清楚地圈定异常位置；对于分离得到的结果，其场值范围可信度有限。

3)小波多尺度分析法对于浅源异常分离效果较好，对于异常特征较为类似的中、深源场分离效果较差。该方法存在小波基选取和分解层数不确定的问题，但已有学者提出了小波分解尺度与深度的大致对应关系[16]，对于小波基的选取也进行了对比总结；同时也使实数尺度小波分析算法得到了发展应用[17]，使重力场分解更加精细，能够进行更准确的重力场分离。

4)重力场垂向分离仍是目前没有得到很好解决的问题之一，这也影响了重力数据处理、反演和解释结果的精度，限制了重力勘探的应用范围。在实践中，除了保证观测数据的准确性之外，应该多收集其他资料，形成先验信息，建立类似模型，利用多种分离方法进行试验，优选最佳分离方法，并使分离结果与先验信息最大限度地吻合，才能获得最佳结果。