输水压力管道钢衬-混凝土-围岩联合承载体分担率研究

茹松楠，李作舟，杨继红，赵亚文，王珏，秦鸿哲，刘杨，龙小刚，赵浩

(1.国网新源控股有限公司，北京 100761;2.陕西镇安抽水蓄能有限公司，陕西 西安 710061;3.华北水利水电大学，河南 郑州 450046)

抽水蓄能电站常采用地下式厂房及地下埋藏式压力管道的结构形式[1]。钢衬-混凝土-围岩组合结构是高HD值(H为管道内压，D为管道直径，HD为H与D的乘积)地下埋管常用的支护方式。一般认为，钢衬-混凝土-围岩组合结构主要由钢衬承受内压，混凝土传递部分压力至围岩，形成联合承载体。对组合结构联合承载机制的研究主要集中在围岩分担率和围岩抗力系数两方面。

在压力管道地下埋管结构设计中，围岩分担内水压力常作为安全储备。在实际工程中，围岩对内水压力的分担情况受围岩类别的影响较大，围岩情况较好时，实测的围岩分担率可达89%[2]。许多学者对围岩分担率进行了研究。王伟等[3]通过有限元数值计算对混凝土衬砌不同缝隙值的敏感性进行了研究，当不存在缝隙且围岩为Ⅱ～Ⅲ类时，围岩分担率最大可达 50.58%。柴建峰等[4]通过FLAC软件对不同缝隙值、混凝土强度、钢衬壁厚、围岩抗力系数的敏感性进行分析，当不存在缝隙时，“垫层 + 围岩”分担率最大可达61%，其对内水压力的分担作用是显著的。柴建峰等[5]还对不同钢衬壁厚、不同设计内水压力组合条件下的钢衬-混凝土垫层-围岩组合结构进行分析，认为钢衬厚度较小时，有利于组合结构联合承载，并计算了钢衬厚度为26 mm时，围岩分担率为71%。汪碧飞等[6]采用三维有限元模拟了岔管、回填混凝土与围岩的联合承载体，计算结果表明，混凝土衬砌对围岩分担率有一定的影响。目前，已有的成果主要通过数值模拟的方法研究钢衬厚度、混凝土衬砌、组合结构间隙等因素对围岩分担率的影响，但针对不同围岩类别，研究围岩分担率变化的成果较少。且在已有的研究方法中，围岩分担率定义为埋管状态下环向应力平均值与明管状态下环向应力平均值相比所减少的百分比[7]。这种定义方法认为混凝土衬砌仅起传递荷载的作用。然而，对钢衬-混凝土-围岩变形分析时发现，混凝土也在承载中产生一定变形[5]。这表明混凝土衬砌在组合结构中分担了荷载，仅仅考虑钢衬和围岩的承载与实际承载情况不符。

围岩抗力系数是隧洞支护结构中的重要参数。围岩抗力系数k为使洞壁围岩产生一个单位径向变形所需要的压力。单位抗力系数k0是指洞室半径为100 cm时的抗力系数值。方钱宝等[8]通过现场平板荷载试验，研究了隧洞平面不同位置处的围岩抗力系数的变化。唐爱松等[9]采用径向液压枕法测量洞室抗力系数，较好地反映了围岩的各项异性。涂洪亮等[10]采用3DEC离散元软件模拟了径向液压枕法测围岩抗力系数的过程，分析了在岩石弹性模量、泊松比、节理间距、节理倾角、节理法向刚度等影响因素作用下抗力系数的分布规律。此外，理论分析也是抗力系数研究的重要部分。许多学者在弹塑性理论分析的基础上，引入不同的强度准则，考虑围岩裂纹开展、蠕变、剪胀等效应，得到了较高精度的围岩抗力系数计算公式[11-16]。整体而言，围岩抗力系数计算的理论有一定进展，但分析过程中采用简化的计算模型，导致理论分析结果与实际测量结果不一致。

本文结合镇安抽水蓄能电站输水压力管道工程实际，应用FLAC3D有限差分软件，采用Hoek-Brown模型对不同类别围岩工况下的压力管道进行计算分析，模拟水压法试验过程，分析抗力系数的变化。在此基础上，分析围岩分担率的变化，提出一种考虑混凝土衬砌承载的分担率计算方法。

1 输水管线三维数值分析

1.1 工程概况

镇安抽水蓄能电站位于陕西省西南部，秦岭山脉腹地，东秦岭主峰——太白山东麓。输水管线围岩主要为花岗闪长岩，工程地质勘察结果表明，该工程区内分布有Ⅱ～Ⅴ类围岩，围岩物理力学参数见表1。

表1 围岩物理力学参数

输水管线剖面图如图1所示，该段采用60 mm厚、管径6.5 m的Q690D钢衬，钢衬材料密度为78.5 kN/m3、弹性模量为206 GPa、泊松比为0.3。钢衬圈外部间隔1 m加设高200 mm、厚26 mm的加劲环。洞室开挖直径为7.9 m，在顶拱范围内梅花型布置注浆锚杆，锚杆长度4.5 m、直径25 mm，间排距1.5 m。

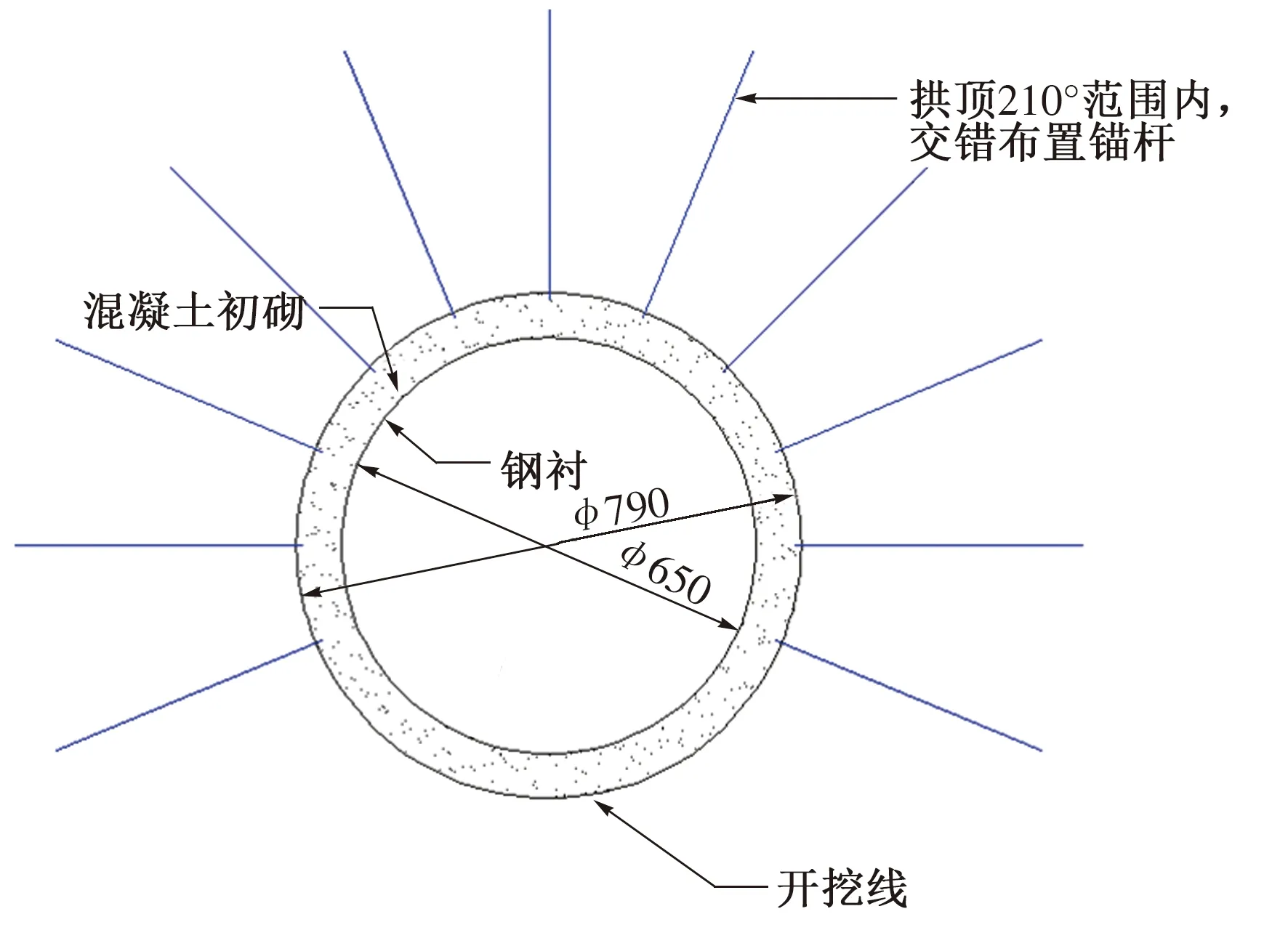
图1 中平段输水管线剖面图(单位：cm)

1.2 数值计算模型及参数

以(0，0，0)点为输水管道中心，向上、下、左、右各扩展100 m，建立中平段输水管线模型，如图2(a)所示,洞室附近的网格划分如图2(b)所示(图例中的“5”代表围岩，“6”代表混凝土衬砌，“7”代表洞室开挖部分)。由图2(a)可知，模型由围岩、混凝土衬砌和洞室开挖部分组成。钢衬部分采用shell单元模拟，采用各向同性，钢衬弹性模量206 GPa，泊松比0.3，厚度60 mm；钢衬外部加劲环采用beam单元模拟，如图2(c)所示。锚杆采用cable单元进行模拟，如图2(d)所示。结构单元参数见表2和表3。

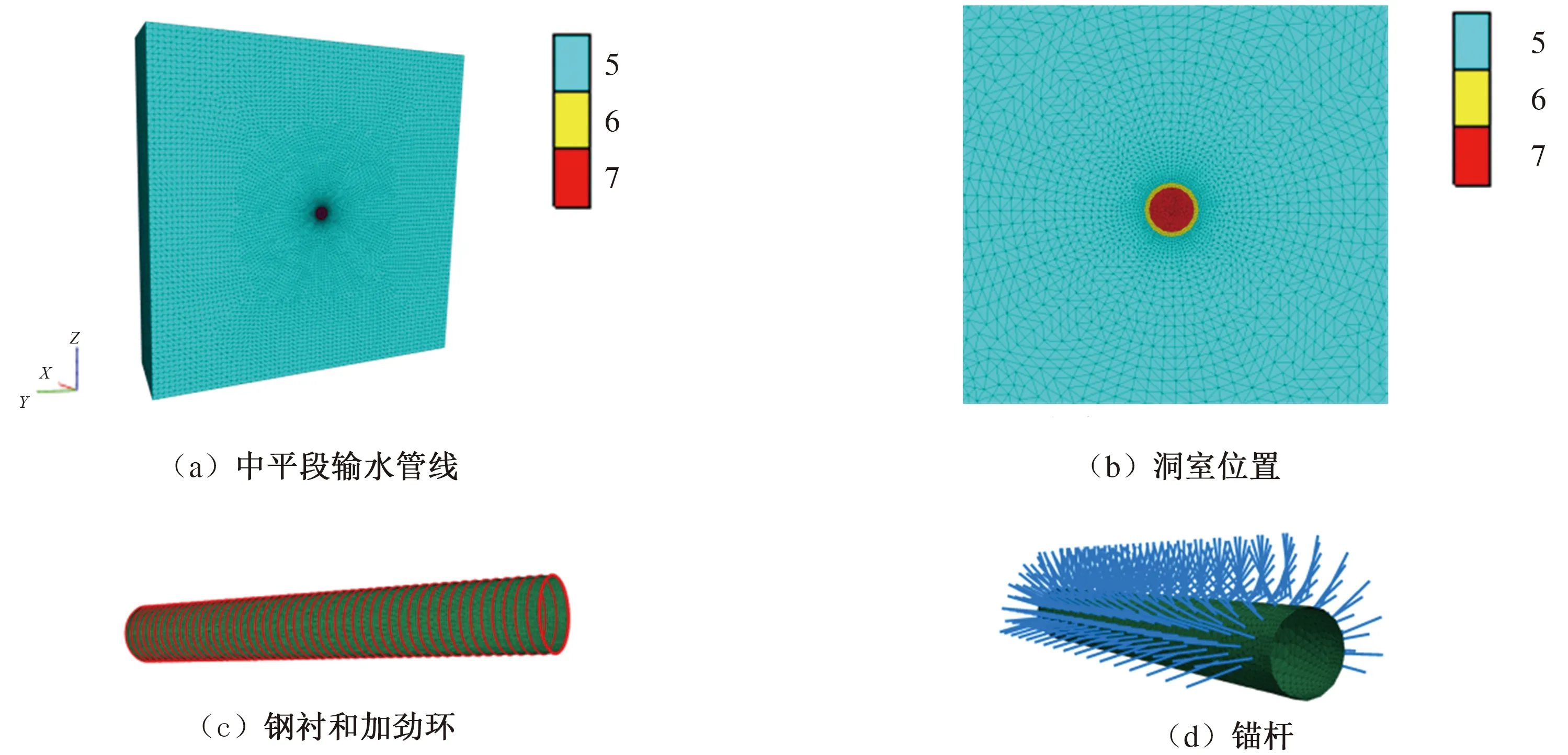
图2 计算模型

表2 beam结构单元参数

表3 cable结构单元参数

1.3 围岩强度准则选取

Hoek-Brown强度准则考虑了岩块强度、结构面组数、所处应力状态对岩体强度的影响等，是隧洞稳定性计算常用的一种强度准则。广义Hoek-Brown经验强度准则表达式为：

(1)

式中：σ1、σ3分别为岩体破坏时的最大、最小主应力，MPa；σci为岩块单轴抗压强度，MPa；mb为与岩性和风化程度有关的经验参数；a为与岩体特征有关的常数；s反映岩体破碎程度，其取值范围为0～1，破碎岩体取0，完整岩体取1。

根据地质调查结果，Heok-Brown模型取值见表4。

表4 Hoek-Brown模型参数

1.4 计算模型加载

在进行数值分析计算时，在模型顶部施加2.5 MPa法向应力，模拟模型顶部的岩土体重量，并采用自重生成初始应力。通过对部分模型开挖，形成围岩、围岩-混凝土衬砌组合结构和钢衬-混凝土-围岩组合结构3种模型。对3种模型进行加载，模型加载工况见表5。

表5 模型加载工况

2 抗力系数计算

2.1 围岩抗力系数分析

对工况1进行加载，模拟隧洞水压法试验过程，在隧洞内壁设置8个监测点，点位布置如图3所示。

图3 监测点位布置简图

规定洞壁径向位移以向外扩张为正，向内压缩为负，围岩加载后径向位移随径向压力变化的曲线如图4所示。由图4可知：随着内壁压力增大，监测点位移线性增大，径向压力-位移曲线斜率的倒数，即为抗力系数；Ⅱ类与Ⅲ类围岩的位移变化曲线相似，1、5点处径向位移为负值，且基本重合，3、7两点位移为正，也基本重合。这说明在地应力和内压作用下，1、5两点向内部压缩变形，3、7两点向外部扩张变形，洞室上下、左右变形量一致。由图4还可以看出：当围岩类别为Ⅳ类时，1、5两点径向位移不再重合，洞室下部向内部的压缩变形大于1点处向内的压缩变形；当围岩类别为V类时，1点处的位移仍为向内压缩，5点处的位移则为向外扩张。导致这一变化的原因是，当围岩的破碎程度上升，围岩的自稳能力明显下降。在工况1条件下，以1.6 MPa内压作用下的剖面位移图为例，如图5所示。由图5可知，在洞室内壁加载过程中，Ⅱ、Ⅲ、Ⅳ类围岩可以在顶拱位置形成一个位移较小的承载拱圈抵抗上部岩体自重，V类围岩由于过于破碎，难以在顶拱位置形成拱圈，岩体自重向下加载在洞室内壁处，所以导致1、5两点处的位移方向都是垂直向下的。

图4 不同围岩径向压力与位移的关系曲线

图5 1.6 MPa水压加载下不同围岩的位移云图

由位移-压力曲线得到的抗力系数k和单位抗力系数k0见表6。

表6 Hoek-Brown模型围岩抗力系数和单位抗力系数

由表6可知，Ⅱ类围岩的单位抗力系数为116～166 MPa/cm，Ⅲ类围岩的单位抗力系数为42～65 MPa/cm，Ⅳ类围岩的单位抗力系数为13～19 MPa/cm，V类围岩的单位抗力系数为4～7 MPa/cm。围岩的单位抗力系数取值范围与地质调查报告结果基本一致。

隧洞断面各监测点的单位抗力系数取值如图6所示。由图6可知，受地应力和围岩类别的影响，围岩的单位抗力系数在环向具有各项异性，Ⅱ类围岩在1、5两点处最大，Ⅲ～Ⅴ类围岩在3、7点处最大。

图6 Hoek-Brown模型围岩洞室内壁单位抗力系数分布图(单位：MPa/cm)

对工况1采用Mohr-Coulomb模型，加载模拟隧洞水压法试验过程。得到Mohr-Coulomb模型下，各监测点的抗力系数和单位抗力系数，见表7。对比表7、表6可知：Mohr-Coulomb模型计算得到的抗力系数略小于Hoek-Brown模型下的抗力系数，且随着围岩类别从Ⅱ类到V类，二者之间的差值逐渐减小；Hoek-Brown模型下的抗力系数更接近于地质勘察得到的抗力系数。这说明Hoek-Brown模型更适用于考虑围岩类别的计算。

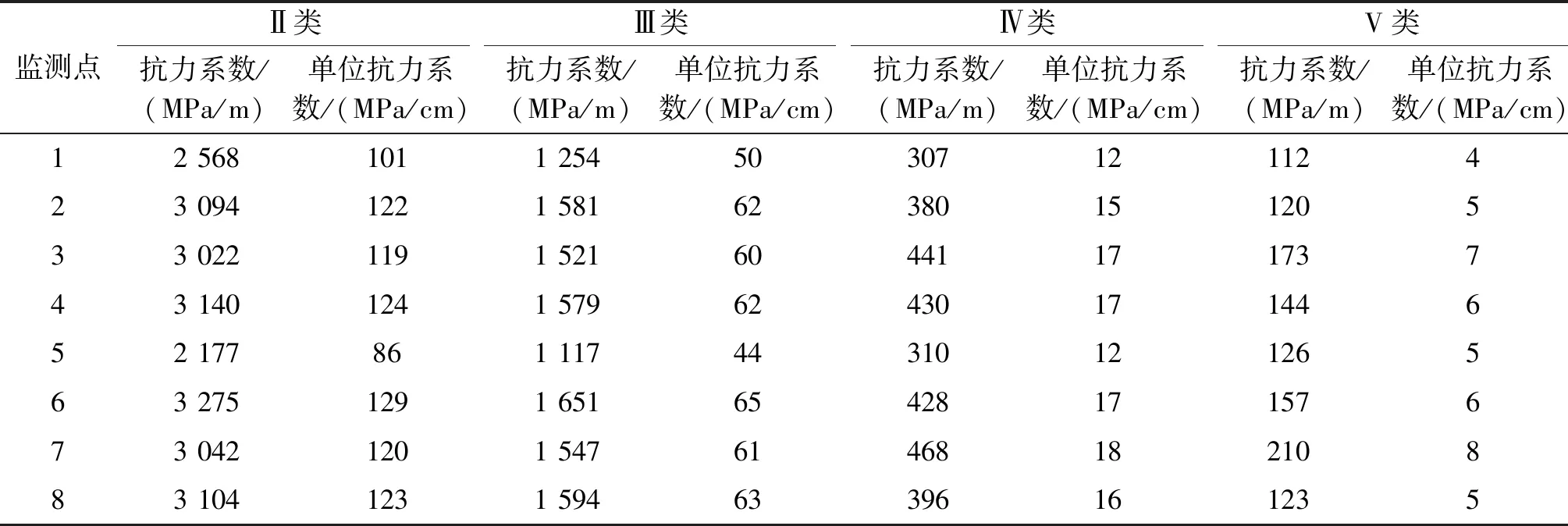
表7 Mohr-Coulomb模型围岩抗力系数和单位抗力系数

隧洞断面各监测点的单位抗力系数取值如图7所示。对比图7和图6可以看出：Ⅱ类围岩下，Hoek-Brown模型的单位抗力系数最大值在1、5点处，Mohr-Coulomb模型的单位抗力系数最大值则在3、7点处；其余围岩类别下，单位抗力系数在环向的分布规律一致。

图7 Mohr-Coulomb模型围岩洞室内壁单位抗力系数分布图(单位：MPa/cm)

2.2 围岩-混凝土衬砌组合结构抗力系数kc

对工况2进行加载，模拟隧洞水压法试验过程。对围岩-混凝土衬砌组合结构加载后，径向位移随径向压力的变化与围岩的基本一致。围岩-混凝土衬砌组合结构在内水压力作用下，位移呈线性增大。通过线性拟合分析，得到围岩-混凝土衬砌组合结构抗力系数kc,结果见表8。对比表8、表6可以看出，围岩-混凝土衬砌组合结构的单位抗力系数明显增大，且围岩类别越差，单位抗力系数增大越明显。

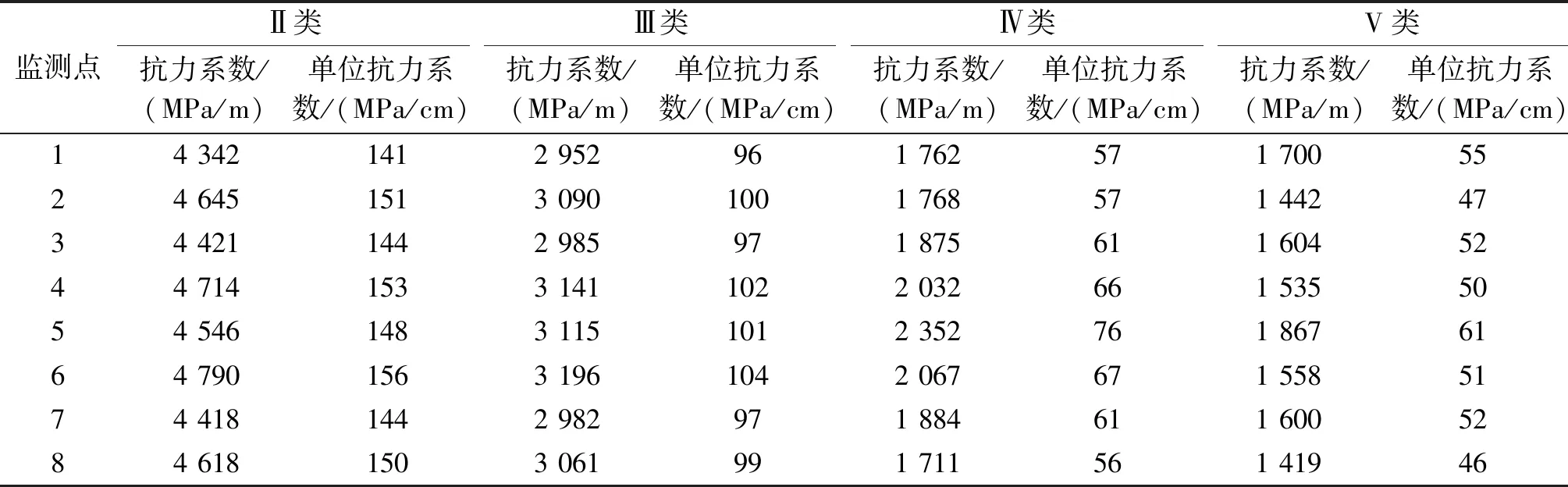
表8 围岩-混凝土衬砌组合结构抗力系数和单位抗力系数

围岩-混凝土衬砌断面各监测点的单位抗力系数取值如图8所示。对比图8和图6可知，围岩-混凝土衬砌组合结构的单位抗力分布在环形断面上更为均匀，这更有利于围岩-混凝土衬砌组合结构的承载。

图8 围岩-混凝土衬砌组合结构内壁单位抗力系数分布图(单位：MPa/cm)

3 围岩荷载分担率计算

3.1 围岩分担率理论计算

本文采用二维弹性体厚壁圆筒理论、平衡条件与围岩的变形相容条件计算围岩分担率λ[2]。该方法计算围岩分担率时，将混凝土和围岩的承载压力之和与总压力比较，实际得到的分担率为围岩-混凝土衬砌组合结构的分担率，具体计算公式如下：

(2)

式中：P为内水压力；r1为钢管内半径；Δ为缝隙宽度；t为管壁厚度；Es为钢衬弹性模量；Ec为混凝土弹性模量；Er为围岩的弹性模量；μr为围岩的泊松比；r3为混凝土衬砌外半径。

本文并未考虑缝隙的存在，缝隙宽度Δ为0。根据该公式计算得到不同围岩的分担率见表9。

表9 围岩分担率理论计算结果 %

3.2 围岩分担率线弹性计算

对工况3进行加载，模拟钢衬-混凝土-围岩组合结构承受内水压力的过程，并分别记录开挖洞室内壁上1—8各监测点的位移和混凝土衬砌内壁1—8各监测点的位移。在模拟内水压力时，分0.8、1.6、2.4、3.2 MPa四级加载，每级均比上一级增加0.8 MPa的内水压力。在四级加载下，洞室内壁上1—8各监测点的位移依次减去前一级位移，得到增加0.8 MPa内水压力所引起的围岩位移变形量Δr，同样处理混凝土衬砌内壁1—8各监测点的位移，得到增加0.8 MPa内水压力所引起的混凝土衬砌位移变形量Δc。在前文中，通过模拟隧洞水压法试验，得到了围岩变形的线弹性抗力系数k和围岩-混凝土衬砌的线弹性抗力系数kc。根据位移变形量和抗力系数，计算得到产生位移变形量所需要的内水压力值，即围岩或围岩-混凝土衬砌组合结构所承受的内水压力值。具体计算公式如下：

Pr=kΔr;

(3)

Pc+r=kcΔr;

(4)

Pc=Pc+r-Pr;

(5)

Ps=P0-Pc+r。

(6)

式中：Ps为钢衬承受的内水压力；Pc+r为围岩-混凝土衬砌组合结构承受的内水压力；Pc为混凝土衬砌承受的内水压力；Pr为围岩所承受的内水压力。

按此方法计算得到的各监测点钢衬-混凝土衬砌-围岩三者之间的分担率见表10。表10中V类围岩的荷载分担率仅为4%。这与之前的分析——V类围岩较为破碎，无法组成有效的承载拱形结构，围岩分担率应急剧减小的结果一致。说明了采用线弹性方法计算得到的围岩分担率符合实际结果。

表10 钢衬-混凝土-围岩荷载分担率 %

在钢衬-混凝土-围岩组合结构中，混凝土衬砌不仅起传递荷载作用，也具有明显的承载作用。将采用线弹性计算得到的围岩分担率与理论计算结果相比较，可以发现Ⅳ类、V类围岩下的钢衬分担率明显低于理论计算结果。降低部分的荷载主要由混凝土衬砌承担。

图9为钢衬、混凝土、围岩3部分在不同围岩类别下的分担率变化曲线。从图9可以看出：随着围岩类别从Ⅱ类到V类，围岩的承载能力逐渐下降，其中Ⅱ、Ⅲ、Ⅳ类围岩的荷载分担率下降明显，Ⅳ类到V类围岩的分担率下降趋势减弱；混凝土衬砌的荷载分担率在Ⅱ类到Ⅲ类围岩时明显增加，在Ⅲ类到V类围岩条件下，其增加趋势有所减缓；钢衬的荷载分担率随围岩类别的变化相对较小，在Ⅲ类到Ⅳ类围岩条件下，钢衬的荷载分担率有明显的增加。

图9 钢衬-混凝土-围岩荷载分担率变化曲线

4 结论

本文结合镇安抽水蓄能电站输水压力管道工程实际，采用Hoek-Brown模型，通过FLAC3D分析了不同类别围岩对钢衬-混凝土-围岩组合结构承载的影响，得出如下结论：

1)Hoek-Brown 强度准则计算的围岩抗力系数大于Mohr-Coulomb准则的计算结果。Hoek-Brown 强度准则计算的结果与工程地质勘察报告提出的抗力系数基本一致，更符合工程实际。

2)受地应力和围岩类别的影响，围岩的抗力系数在环向上具有各向异性。Ⅱ类围岩的单位抗力系数在隧洞拱顶和底部两点最大。Ⅲ、Ⅳ、V类围岩的单位抗力系数在隧洞侧壁位置处最大。

3)通过线弹性理论计算钢衬-混凝土-围岩荷载分担率，从钢衬、混凝土、围岩三者的分担率来看，在组合结构中，混凝土不仅起到传递荷载的作用，也具有明显的承载作用。

4)输水压力管道联合承载体荷载分担率计算结果表明，Ⅱ、Ⅲ、Ⅳ类围岩的荷载分担率下降明显，Ⅳ～Ⅴ类围岩的分担率下降趋势减弱。混凝土衬砌的荷载分担率在Ⅱ～Ⅲ类围岩条件下明显增加，在Ⅳ～Ⅴ类围岩条件下时，其增加趋势有所减缓。钢衬的荷载分担率随围岩类别变化相对较小，在Ⅲ～Ⅳ类围岩条件下，钢衬荷载分担率明显增加。