轨道车辆轮轨等效锥度管理措施研究

戴焕云，杨震寰，干 锋

（西南交通大学牵引动力国家重点实验室，四川成都 610031）

1 引言

轮轨等效锥度是影响轨道车辆系统动力学性能的重要因素。早在20世纪60年代，A.H.Wickens便建立了车辆系统的运动方程研究磨耗后踏面对车辆运行稳定性的影响，他指出，磨耗后踏面的锥度对车辆蛇行运动稳定性有着重要的影响。近年来，我国高速铁路网逐渐增加，车轮和钢轨磨耗的情况日趋复杂，高速动车组运营中曾出现因等效锥度异常造成动车组产生蛇行失稳的情况，主要表现为车体晃动、转向架失稳报警及车体抖动，极大地影响了车辆乘坐的平稳性和舒适度。O.Polach指出等效锥度与轮对蛇行运动分叉类型有密切关联，并提出一种基于等效锥度的非线性参数，该参数对蛇行运动的分叉类型有重要影响。

综上所述，等效锥度是轮轨关系的直接评价指标，但目前针对如何应用等效锥度对轮轨关系进行准确评价尚未出台具体的标准，所以对等效锥度的管理显得尤为重要。由于轮轨廓形对等效锥度有重要的影响，因此需通过检测轮轨廓形的变化监测等效锥度的动态变化，并建立轮轨管理系统，进而指导轮对镟修以及钢轨打磨。

2 等效锥度的计算及其影响因素

轮对和钢轨在实际应用过程中均表现出不同程度的磨耗特征，容易导致车辆出现晃车和抖车现象，严重降低乘坐舒适性并威胁行车安全。由此可见，轮轨接触关系会直接影响车辆的安全运行品质。等效锥度是评价轮轨接触关系的重要指标，可以真实有效地反应轮轨接触关系，对车辆在线路上运行时的动力学性能预测评估有重要的参考价值。

2.1 等效锥度的计算

2.1.1 简化法

理想的锥形踏面车轮在滚动圆附近是一段斜度为常数μ的直线段，在轨道车辆领域将常数μ称为车轮锥度。锥度μ可使用下式计算：

式（1）中，rL，rR分别为左右轮滚动圆半径；Δr为轮径差；y为轮对横移量。

对于实际的车轮踏面外形，μ会随着y的变化而变化，并不是一个定值，此时由左右轮滚动圆半径rL和rR简化计算出的锥度μ即为等效锥度。

2.1.2 等效线性化法

自由轮对在轨道上的运动可由运动学微分方程表示为：

式（2）中， 为轮对横移加速度；e为接触点跨距；r0为名义滚动圆半径；Δr为轮径差；v为轮对前进速度。

y的解为正弦波，设其波长为λ，若车轮踏面外形为理想的具有γ角的锥形，则有

习近平指出：改革开放以来党的全部理论和实践的主题是中国特色社会主义。“中国特色社会主义道路是实现社会主义现代化、创造人民美好生活的必由之路，中国特色社会主义理论体系是指导党和人民实现中华民族伟大复兴的正确理论，中国特色社会主义制度是当代中国发展进步的根本制度保障，中国特色社会主义文化是激励全党全国各族人民奋勇前进的强大精神力量。”[1]40年改革开放伟业的时代变换是从社会主义建设新时期到中国特色社会主义新时代，目前我们的党和国家正昂首阔步走在中华民族伟大复兴的宽阔大道上。

式（3）即为Klingel公式。

实际上，车轮踏面不是理想的锥形，而是存在磨耗的踏面。此时可采用线性化法，使用等效锥度tanγe代替tanγ；通过给轮对横移量y以初始幅值y0，再对式（2）进行求解，导出轮对以幅值2y和波长λ的周期运动；最后应用式（3）计算得到轮对横移量为y0时的等效锥度，即

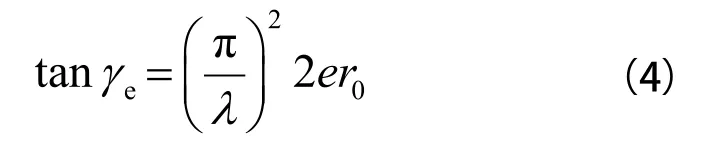
2.2 等效锥度的影响因素

由等效锥度的计算过程可以看出，轮对内侧距、轨距、轨底坡、车轮型面、钢轨型面均会对等效锥度产生较大影响。图1给出了新镟修踏面和磨耗后踏面的等效锥度计算结果。由图可知，车轮型面不同，等效锥度的计算结果差异较大。

图1 等效锥度计算结果

3 等效锥度与车辆系统稳定性的相关性分析

根据我国多年的铁路运营经验，轨道车辆系统的蛇行失稳主要有车体蛇行和转向架蛇行2种形式。车体蛇行也称为一次蛇行，其主要表现为车体的低频晃动；转向架蛇行也称为二次蛇行，其主要表现为转向架失稳报警或车体异常抖动。本文将从等效锥度的角度对上述2 种蛇行失稳形式进行阐述。

3.1 晃车机理及应对措施

某型动车组在车轮镟修后出现了晃车现象，图2展示了晃车时列车的平稳性指标和振动频率。由图可知，晃车时车辆的平稳性指标超过合格限值3.0，且振动主频为1.50 Hz。

图2 晃车区段平稳性及振动频率

对钢轨廓形和新镟修车轮踏面进行测试后，计算得到LMB_10型实测踏面和实测钢轨型面匹配后的等效锥度如图3所示。由图可知，轮轨实际等效锥度均小于0.10，等效锥度过小。如图4所示，通过实测武广高速铁路钢轨廓形可知，该线路钢轨内轨距角过度打磨，轮对接触点集中在轨顶，使得车辆实际轮轨等效锥度过低。

图3 实测轮轨匹配下的等效锥度

图4 实测钢轨廓形

取车轮踏面磨耗后的列车进行对比，测试结果如图5所示。由图可知，当车轮磨耗后，车体横向加速度幅值显著降低，且振动主频不再明显，车体已不存在晃车现象。

图5 实测车轮磨耗前后车体横向加速度

研究还发现，当抗蛇行减振器动态刚度过大时，也容易出现车体晃动问题。如图6所示，安装动态刚度较小的T60抗蛇行减振器后，车体横向加速度幅值会明显降低，且振动主频不再明显，可有效改善晃车问题。

图6 2种抗蛇行减振器对车体横向加速度的影响

综上所述，车体低频横向晃动是由车轮与钢轨匹配后等效锥度偏小，加之抗蛇行减振器动态刚度较大造成的。解决的措施为适当减小抗蛇行减振器的动态刚度，并保证轮轨之间合理的轮轨匹配关系。

3.2 转向架失稳报警及抖车的机理和分类

转向架失稳报警的机理是实际轮轨等效锥度过大，使转向架出现7～9 Hz的蛇行失稳。如果车体的结构弹性模态与转向架蛇行运动频率接近，则会激发车体的模态振动，使车体出现剧烈抖动，即出现“抖车”现象。如图7和图8所示，通过对实测线路打磨前后的钢轨廓形进行分析可知，由于钢轨内轨距角处凸起，使磨耗车轮与抖动区段钢轨匹配等效锥度突然增大，引起转向架蛇行运动频率陡升，从而造成车辆转向架失稳报警或抖车现象。在钢轨打磨后，其内轨距角处的高度下降，构架的横向振动频率也会显著降低。

图7 钢轨打磨前实际等效锥度

目前，我国高速动车组出现的转向架报警或抖车现象的分类如表1所示。由表可知，我国的动车组转向架报警或抖车现象根据失稳区段可分为局部区段失稳、跨线或换线运行造成的多区段失稳和单线路多区段失稳。对于局部区段抖车报警，最经济的解决方法是进行局部钢轨打磨。对于跨线或换线运行造成的多区段失稳，由于只能通过踏面镟修解决，但这会缩短镟修里程，是不经济的，因此应以车轮在不同线路上存在相同的等效锥度为目标，制定统一标准，打磨出统一的钢轨廓形。对于单线路多区段失稳，可采用钢轨打磨和车轮镟修的方法解决。

表1 转向架失稳报警或抖车现象的分类

3.3 名义等效锥度取值研究

国际铁路联盟标准UIC 519-2004 Method for Determining the Equivalent Conicity 定义的名义等效锥度是指轮对横移量为3 mm下的等效锥度。但是仅由3 mm下的等效锥度评价轮轨接触关系并预测车辆在实际运行中的蛇行运动稳定性是不全面的，特别是近年来从国内的转向架报警和抖车现象中发现，当等效锥度较大且出现“负斜率”增长时，车辆容易出现转向架报警或抖车问题。

需要指出的是，当等效锥度呈现“负斜率”增长特性时，3 mm下的等效锥度数值往往较小，如图9所示，该实际轮轨匹配下的3 mm等效锥度数值为0.38。如图10所示，以3 mm下的等效锥度数值仿真计算出的刚性转向架蛇行频率为6 Hz，该频率与图11中实测的转向架蛇行运动频率8 Hz有较大差异。

图9 实际轮轨匹配下的等效锥度

图10 仿真计算的转向架蛇行运动频率

图11 实测刚性转向架横向加速度

当轮对横移量为1.5 mm时，其等效锥度数值为0.65，使用该等效锥度数值进行仿真计算后，得到刚性转向架蛇行运动频率为8 Hz，与实测转向架横向加速度频率结果较为吻合。本文建议取实际轮轨廓形进行匹配，使用轮对横移量为1.5 mm处的等效锥度作为评价轮轨接触关系和预测车辆运行稳定性的重要参考。

4 等效锥度检测管理

4.1 车辆运行状态检测

采用如图12所示车辆运行状态便携式检测监测设备可准确方便地获取车体平稳性、舒适度及构架横向加速度等车辆运行评价指标。该测量设备具有精度高、可实时采集、方便现场使用等优点。

图12 车辆运行状态便携式检测监测设备

4.2 车轮踏面廓形检测

车轮踏面的测试精度对轮轨关系各项指标的计算具有很大影响。数字激光测量技术具有测量精度高、性能稳定以及抗干扰能力强的优点。便携式车轮踏面廓形测量仪采用数字激光传感器技术，具有测试精度高、操作方便、便于现场应用等优点，可以有效检测车轮踏面磨耗量、轮径差、等效锥度及QR值等10余项指标，能够综合评价轮对磨耗状态，如图13所示。

图13 车轮踏面廓形便携式检测

4.3 钢轨廓形检测

为更准确地掌握真实的轮轨接触状态，对实际钢轨廓形的测量具有重要意义。如图14所示，采用高速2D激光检测技术的钢轨廓形检测仪可以连续测量钢轨廓形，动态反应轨道的几何不平顺状态、钢轨波磨以及钢轨表面缺陷。其检测精度能够满足轮轨接触关系的动态计算要求，可结合车轮踏面测试结果准确计算实际等效锥度，然后根据计算结果对车轮进行更加合理的镟修，为制定钢轨打磨周期提供重要依据。

图14 车载式钢轨廓形检测

4.4 等效锥度管理

由前文分析可知，等效锥度是轮轨关系的重要评价指标，能够真实地反应轮轨关系的变化，因此有效地对等效锥度进行管理，建立轮轨关系评价体系，是解决当前轮轨孤立维护的关键。本文基于钢轨廓形和踏面廓形动态检测，进行交叉匹配运算，从而分析实际轮轨接触关系，并通过等效锥度热力图实现对晃车、转向架失稳报警和抖车问题的诊断和预防，如图15所示。等效锥度热力图横轴表示公里标，纵轴表示车轴号，颜色深度表示等效锥度量化值。若沿横轴出现红色带，则表明轮对的磨耗超限，与线路匹配的等效锥度偏大，需要对轮对进行镟修处理；若沿纵轴出现红色带，则表明所有轮对经过该区段对应的等效锥度偏大，线路存在异常磨耗的问题，需要进行打磨维护。因此，可以根据该图掌握轮轨等效锥度状态，有效分析等效锥度异常的成因，并依据实际情况进行钢轨打磨和车轮镟修。

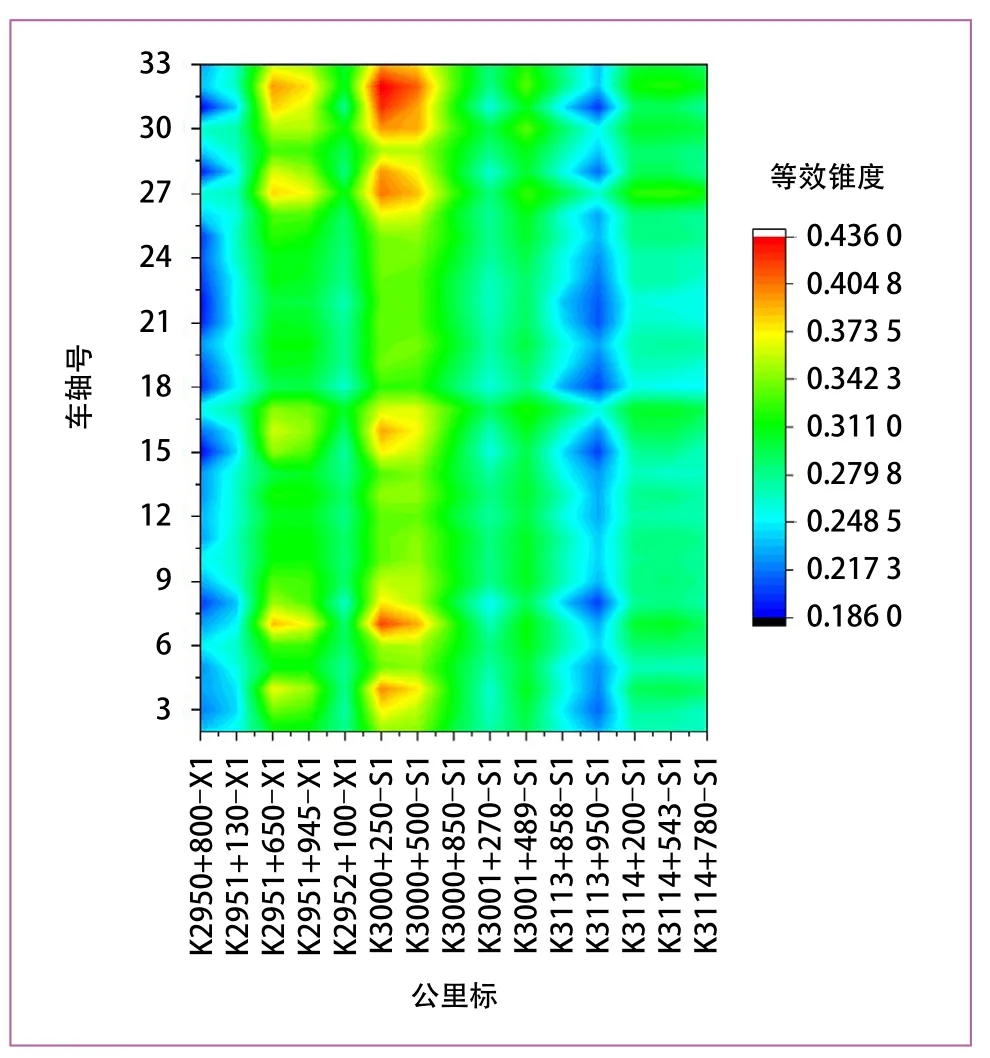
图15 等效锥度热力图

5 结语

本文从等效锥度的角度分析了轨道车辆晃车、转向架失稳报警和抖车的原因，并提出了解决上述问题的相应措施，建议采用轮对横移量1.5 mm处的等效锥度数值作为3 mm等效锥度的补充，用以评价轮轨接触状态并预测车辆运行稳定性。此外，等效锥度作为评价轮轨接触关系的重要指标，应对其进行有效的管理，本文结合车辆运行监测设备、轮轨检测设备进行等效锥度的计算和管理，为轮轨运行健康管理及运行评价提供重要参考，并实现对轨道车辆晃车、转向架失稳报警和抖车问题的诊断和预防，进一步为实现铁路计划修转向状态修提供可靠支撑。