考虑洪水漫延过程的地铁车站人员疏散研究

黄聪，苏栋,2,3，杨磊,2,3，雷国平，黄文,2,3

(1. 深圳大学土木与交通工程学院，广东深圳 518060；2. 滨海城市韧性基础设施教育部重点实验室(深圳大学)，广东深圳 518060；3. 深圳市地铁地下车站绿色高效智能建造重点实验室，广东深圳 518060)

随着社会经济的飞速发展，近年来，土地资源短缺问题日益突出。开发利用地下空间是解决城市发展与土地资源匮乏之间的有效途径。地下空间相对封闭，只有几个出入口与外界相连。当洪水发生时，诸如购物商场，地铁站和建筑物地下室等地下空间很容易被淹没。由于地下洪水的上升速度很快，会造成巨大的经济损失并造成大量人员伤亡。2001年9月台风造成的暴雨淹没了许多地铁站，地铁系统瘫痪[1]。从1992 年到2003 年，伦敦地铁系统遭受了1 200 次以上的洪水袭击，其中200 次以上的地铁停止运行[2]。因此，研究在洪水发生时地下空间的人员疏散以提高疏散效率并减少人员伤亡，是提升地下空间韧性的重要课题。现有的行人疏散模型可以分为2类，宏观疏散模型和微观疏散模型。许多专家利用Pathfinder，Simulex，Anylogic 和STEPS 等相关软件来实现人群疏散的宏观模拟[3-7]。宏观疏散模型主要描述了行人流量，密度和速度之间的关系。但是宏观疏散模型无法区分个人的不同行为，难以直观和定量展示局部的细节的信息，输出的结果与现实相差较大。微观疏散模型[8-28]考虑的个体因素多，计算公式全面而复杂，且往往结合积分学和牛顿力学理论。因此微观模型可以准确地描述个人行为，更加接近现实。微观疏散模型可以分为连续模型和离散模型2类。HELBING等[9]开发的社会力量模型是典型的连续模型，可以观察人流特征。离散模型主要包括格子气模型[11-15]和元胞自动机模型[16-29]。SIMONOVIC 等[29]开发了一种计算机仿真模型，使用系统动力学方法来捕获洪水紧急情况下的人类行为。ZHENG等[25]提出一种结合水灾的疏散模型，通过模拟仿真的数据分析了人员密度、水的上升速度等因素对疏散的影响。张炜[30]以格子气模型为基础，考虑在水灾时人员的心理特性同时，建立了乘客的疏散模型。上述学者在研究洪水对地下空间行人疏散的影响时，主要考虑区域洪水下疏散的宏观特性，且通常只考虑水的深度是随时间上升的阶段，忽略了洪水漫延和行人移动的动态过程。首先建立基于元胞自动机的洪水漫延模型，并且考虑了洪水漫延过程对人员的移动速度和运动方向影响，本文提出一种基于元胞自动机同时分析洪水漫延和人群疏散的新方法，在此基础上研究洪水漫延对人员撤离过程动力学的影响。

1 模型

1.1 洪水漫延模型

1.1.1 计算中心元胞向相邻元胞转移的体积

本文采用基于WCA2D的CADDIES-2D进行洪水漫延模拟[31]。该模型采用正方形网格中的冯诺依曼领域进行洪水动力学计算。WCA2D 洪水漫延模型包括以下2个步骤：根据元胞间体积差计算中心元胞向下游各个元胞转移水量的权重；中心元胞流入各个下游入元胞的体积。

1) 根据元胞间体积差计算中心网格向下游各个网格转移水量的权重；根据每个元胞的水位计算中心元胞与相邻元胞的水位差，其中低于中心网格水位的网格被称为下游网格，即其与中心网格的水位差为正值，且中心网格的水流流向下游网格。水位差乘以网格的面积即得到中心网格与下游网格之间的水量体积差ΔV0,i，由体积差计算中心网格向下游各个网格转移水量的权重。计算公式如下：

其中：m是元胞的数量；i是所计算的元胞的索引；l0是中心元胞的水位，m；li是所计算的元胞的水位，m；Δl0,i为在中心元胞和相邻元胞之间的水位差，m；Ai为元胞的面积，m2；ΔV0,i是中心元胞与第i个相邻元胞之间的可体积差，m3；ΔVmin是下游元胞的最小体积差，m3；ΔVmax是下游元胞的最大体积差，m3；ΔVtot是中心元胞与下游各个元胞的体积差总和，m3；w0为中心元胞保留水量的权重。

2) 中心元胞流入各个下游元胞的体积；该模型用曼宁公式和临界流方程限制中心元胞向相邻元胞转移的水量，每个下游元胞的权重和离开中心元胞的总体积计算流入下游元胞的体积：

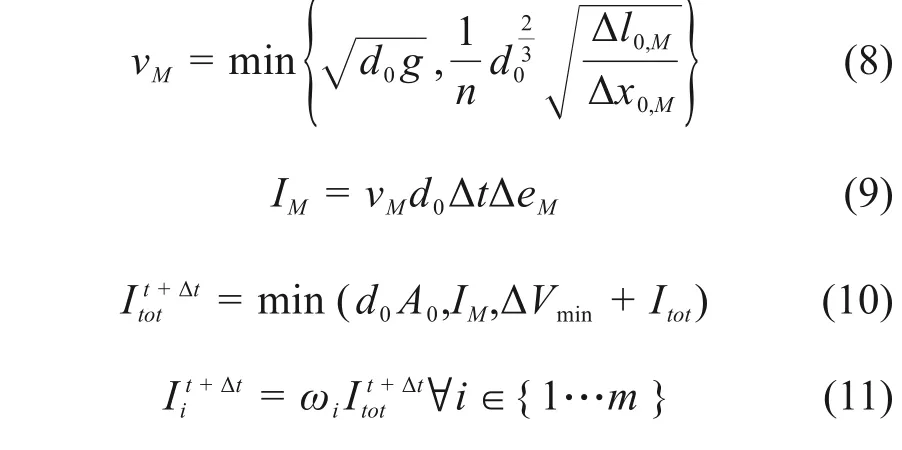
其中：vM是从中心元胞到权重最大的相邻元胞间的最大速度，m/s；Δl0,M为在中心元胞和与权重最大的元胞间的水位差，m；Δx0,M为中心元胞和权重最大的元胞中心之间的距离，m；d0是中心元胞的水位，m；IM是转移到权重最大元胞的体积，m3；Δt是时间步长，s；ΔeM为权重最大元胞的长度，m；A0是中心元胞的面积，m2；wM是下游元胞权重的最大值；I t+Δt tot是在时间t+ Δt离开中心元胞的体积，m3；ωi是第i个元胞所占的体积权重。

1.1.2 元胞水深更新和速度计算

在WCA2D 模型中，通过计算从上一个时间步中元胞的水深中减去流入下游元胞的体积来更新元胞的水深。式(12)用于更新水深：

1.2 洪水漫延对人员运动行为的影响

洪水对人员疏散的影响包括对人员移动方向和人员移动速度的影响。其主要表现为乘客趋向水浅的位置移动和水深的增加会导致乘客移动速度减小。在本文中，如果元胞的水位高于临界值Ho=0.7 m，将视这个元胞为墙壁或者障碍物。

1.2.1 洪水对行人移动方向的影响

因为洪水漫延会对处于点(i,j)的乘客产生排斥力，导致乘客向水深的元胞移动变得更加困难，因此乘客移动到水浅的元胞概率更大。在有洪水乘客移动到下一个元胞的概率计算公式：

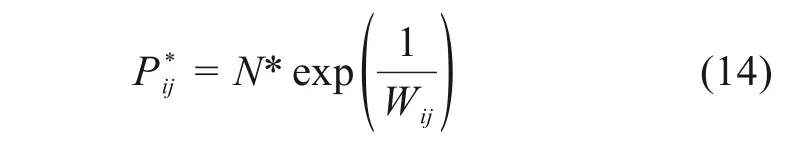
其中：N表示归一化参数，保证P*ij= 1，Wi,j表示乘客避免水灾的行为。

Wi,j反映了避免洪水的行为，它与元胞(i,j)处水的深度成反比。如果元胞(i,j)周围处水深度不全为0，则按式(15)计算：

其中：d**i,j表示在元胞(i,j)处水的深度。

1.2.2 洪水对人员移动速度的影响

行人在地面上行走最大速度为1.5 m/s，它随着洪水深度的增加而减小。速度公式如下[25,30]：

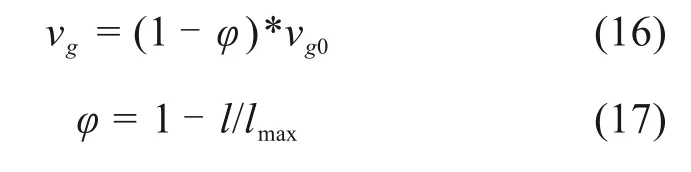
其中：vg是行人速度；φ是由于水深度对行人速度影响因子。l是指在元胞(i,j)处水深；lmax是行人无法行走的临界水深，其设置为lmax=70 cm。

模拟中的每一个元胞的长度和宽度均设置为0.4 m[30]。当没有水灾时，时间间隔Δt=0.27 s，行人可以移动到下一个元胞。当有水灾时，洪水会对行人的移动速度按照式(16)和式(17)进行折减。

1.3 人员疏散模型

在分析洪水漫延过程中行人运动特征的基础上，建立了基于元胞自动机的洪水漫延下人员疏散模型。如图1所示，人员疏散仿真模型采用元胞的大小为0.4 m×0.4 m[30]，采用moore邻域。行人根据概率Pi,j移至相邻元胞，其计算如下：

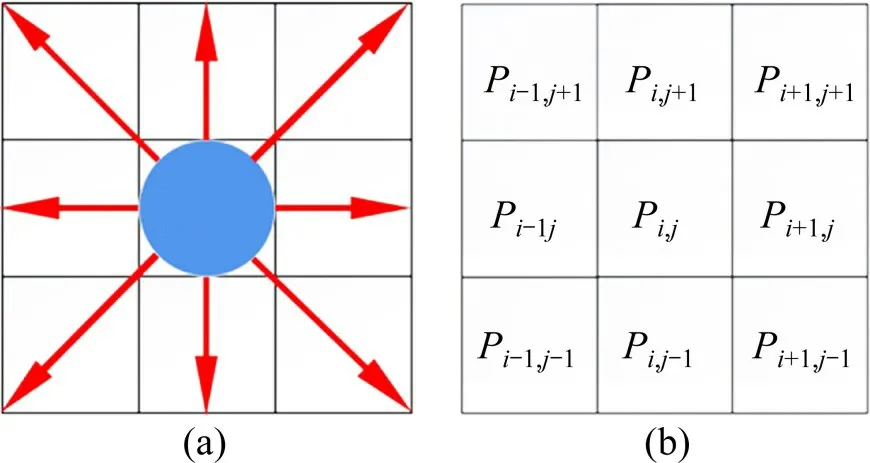
图1 领域和转移概率矩阵Fig.1 Domain and transition probability matrix

N是归一化参数，确保∑Pi,j= 1。Si,j，Di,j和Wi,j表示静态场、动态场和洪水场，kD，kS和kw是缩放参数。ηi,j表示元胞(i,j)是否被墙壁或障碍物占用时。εi,j表示元胞(i,j)是否被行人占据，Si,j描述到出口的最短距离，它的设置与从元胞(i,j)到出口的距离成反比[26]；

Di,j描述个体间有相互吸引的作用[26]。计算如下：

其中：λ是扩散概率；δ是衰减概率。

1.4 模拟仿真流程

1) 该模型是洪水漫延的过程和行人疏散同时运行；

2) 在不考虑任何外部因素的情况下，洪水根据第1.1节进行扩散到周围；

3)根据第1.2 节，洪水漫延会影响行人移动的速度和运动方向；

4)在每个时间步中，根据第1.3 节计算静态场Si,j，动态场Di,j以及水灾场Wi,j，然后计算目标元胞选择概率Pi,j；

5)每个行人根据转移概率Pi,j随机移动到目标元胞。

2 模拟研究

2.1 疏散场景

参照深圳市车公庙地铁车站的站厅结构，设计了一个简单的地铁车站站厅场景进行仿真。车站的长度和宽度为266 m 和102 m，车站一共有5个出入口(长度为6 m)和5 处楼梯，进水口的位置设置在出口2。每个元胞的长度和宽度均为0.4 m[30]，因此地铁车站定义为665 个元胞×355 个元胞，图中黑色的部分为障碍物，白色部分为行走区域。行人在地铁车站内随机分布，最初行人的数量被设定为4 500。参数设置为λ=0.2，σ=0.2，kD=10，kS=10，kW=10[26]。

图2 地铁车站平面示意图Fig.2 Schematic diagram of subway station

2.2 疏散过程

如图4 所示，通过绘制在不同时间间隔t= 0，100，200 和300 s 的情景来研究疏散过程。最初有4 500 个行人随机分布在场景中，出口2 为进水口，红色元胞代表有乘客。行人从地铁站厅撤离到出口，在一定时间间隔后，随着洪水的深度增加，当水的深度小于70 cm 时，行人还能继续移动，当洪水深度上升至70 cm，车站内的行人停止移动。从图4 中可以知，往出口1，3，4 和5 撤离的行人全部疏散成功，只有往出口2 的行人被困在地铁车站。

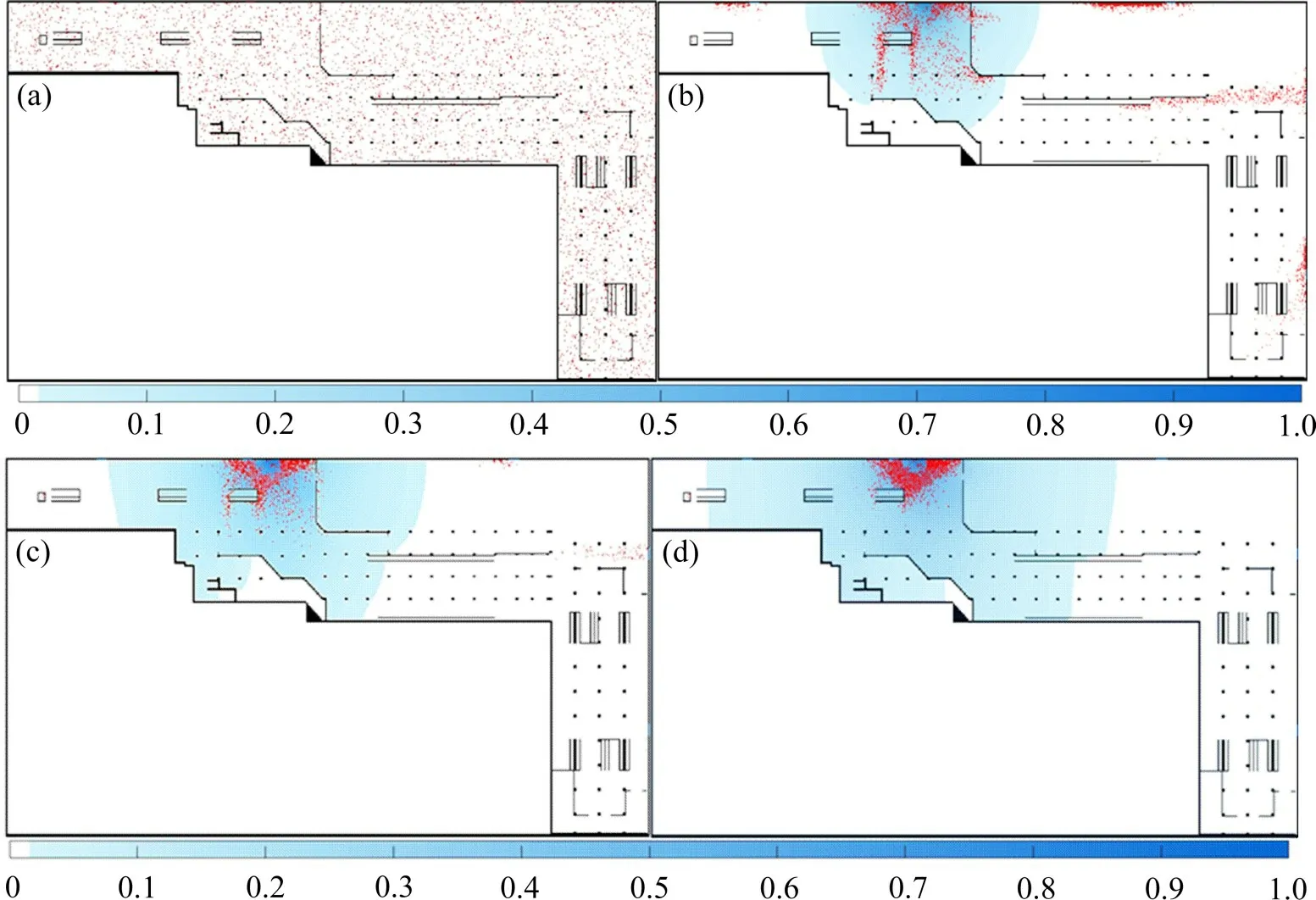
图4 疏散过程Fig.4 Evacuation process

模拟应急疏散人员的数量是4 500 人，在没有洪水时，行人全部疏散，疏散的时间大概是280 s。当发生洪水时，疏散的时间大概是385 s。图3 表示疏散行人的数量与时间的关系。红线表示在地铁车站没有水的情况下，行人正常行走。绿线表示洪水逐渐流入的情况。可以看到，在这2种情况下，虽然疏散的行人都随着时间增加，但是有洪水情况的行人疏散的效率显著低于无洪水的情况。是因为车站内的水深的增加导致乘客被困在车站内。最终，在有洪水时约有943名未疏散的行人被困在车站。

图3 行人疏散与时间的关系Fig.3 Evacuation of pedestrians in relation to time

2.3 不同进水口位置的影响

应急疏散的人员数量设定为4 500 人，出口处的水深为1 m(本文将进水口的流量根据体积公式换算成进水口的水深)，研究在不同的进水口位置进水时，疏散行人的数量与时间的关系。从图5可知，当每个出口分别进水时，疏散的人数随时间增加而快速增加，然后疏散的人数逐渐趋于稳定。当出口1，2，3，4 和5 分别单独进水时，从地铁车站中疏散出的人员数量分别4 099，3 500，3 940，3 679和4 102人。出口1和出口5进水时，能从地铁车站疏散的人数最多且疏散效率最高，出口2 和出口4 进水时从地铁车站疏散的人数最少且疏散的效率最低。可以从疏散过程中可以发现，从不同出口疏散的人数是不同的，疏散行人数量和人员疏散的效率从出口2，出口4，出口3，出口5和出口1依次减少。

图5 疏散行人的数量与进水口的关系Fig.5 Number of evacuated pedestrians in relation to the water inlet

2.4 进水口流量的影响

应急疏散的人员数量设定为4 500 人，研究在相同进水口位置，未疏散行人的数量与进水口的水深的关系(本文将进水口的流量根据体积公式换算成进水口的水深)。从图6 可知，对于不同的出口分别进水时，随着出口的进水深度的增加，未疏散的行人数量也随之增加，但是疏散的效率随之降低。因为随着出口水深的增加，根据式(12)可知水的漫延速度也会增加且水深也会快速增加，因此洪水的影响范围迅速扩大和洪水深度也会迅速增加到70 cm，从而限制行人的移动导致更多的行人被困在水中。在出口1，出口3 和出口5 分别单独进水时，随着进水的深度增加未疏散的人数会快速增加。但是当出口2进水深度增加时，相对其他出口进水时未疏散的人数是最多，但是未疏散的人数缓慢增加。

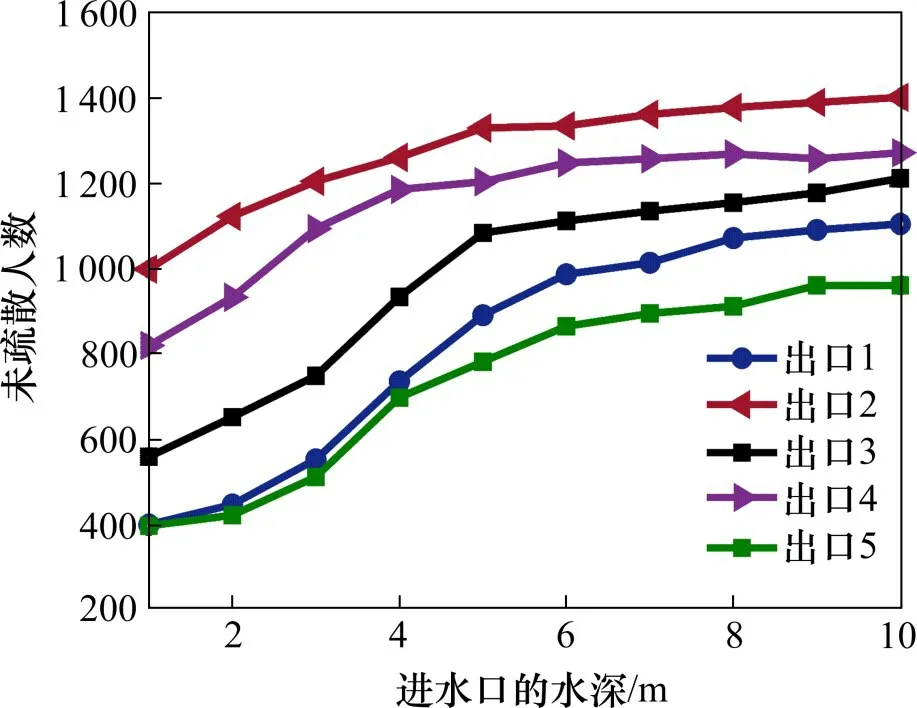
图6 不同的进水口情况下未疏散的行人与进水口水深的关系Fig.6 Relationship between unevacuated pedestrians and water depth at the inlet for different inlet scenarios

3 结论

1) 通过使用一种基于元胞自动机同时分析洪水漫延和人员疏散的新方法，建立洪水漫延下人员疏散的分析模型。仿真模拟结果表明有洪水时行人的疏散效率显著低于无洪水的情况，地下洪水漫延会严重影响行人疏散的效率。

2) 随着进水口位置的变化会对行人疏散的效率造成很大的影响，从而可以有针对性地对出口采取防护措施。在相同的进水口位置，随着进水流量的增加未疏散的人数也迅速增加。

3) 本文只是提出一种同时分析洪水漫延和人员疏散的方法。后续可以结合识别结构BIM 模型的方法，快速构建结构的二维模型，可以将这种方法应用到其他的建筑中，用于研究洪水对人员疏散的动态影响。