基于迭代学习的速度传感器故障诊断研究
张翔,温熙圆,曹宏发,孟红芳,董海鹏,童修伟
(1. 中国铁道科学研究院集团有限公司机车车辆研究所,北京 100081;2. 北京纵横机电科技有限公司,北京 100094)
霍尔式速度传感器已广泛应用于轨道交通和汽车电子产品中,利用基于电磁感应原理的霍尔式速度传感器检测移动设备的速度,进而实现车载设备的防滑控制及车轮不旋转检测等功能[1-3],是保证系统安全可靠运行的重要手段。然而,在车载设备运营过程中,车载轴端速度传感器受扰易引起输出信号异常,危害车载设备正常运营[4]。为此,如何利用有效方法对速度传感器进行安全性检查和维修,保证传感器稳定可靠运行是目前研究的热点和难点[5-7]。传统的速度传感器功能监控和检修多通过人工确认,耗时长效率低,通过故障诊断或健康管理的方法在线监测车载设备的运行状态可大幅提高检修效率和准确性[8]。利用硬件电路对速度传感器进行故障诊断无需占用处理器资源且响应迅速,在出现突发故障时可通过硬件电路隔离故障点,有效避免单一故障点引起的系统联锁故障。然而,受限于工作原理,硬件故障诊断方法多在旋转变压器和光电编码器中使用[9]。通过软件方法进行故障诊断,对不同原理的速度传感器、速度传感器不同种类的故障(如传感器缩针、连接器内电缆扭断、电磁干扰引起的波形异常等)具有更好的普适性。软件故障诊断的定量分析主要包括基于解析模型[10-11]和基于数据驱动的故障诊断方法[12-13]。ZHAI 等[14]利用正交投影法将原始模型降阶,简化原始模型相关属性后构建降阶模型的特征参数,根据特征参数的影响矩阵识别故障。成庶等[15]针对逆变器功率器件开路故障前后的相电流轨迹进行数学建模,根据模型分析数据提取故障特征,利用积分算法实现故障定位。基于解析模型的故障特征参数提取对诊断对象的数学模型建模精度要求较高,建模误差直接映射到诊断过程,易导致诊断结果的偏差。陈大朋[16]提出一种基于迭代学习滤波器的故障诊断算法,能够辨识执行器和传感器的未知故障。李笑梅等[17]提出一种基于集合经验模式分解和径向基函数神经网络相结合的滚动轴承故障诊断方法,根据列车滚动轴承振动信号精确识别轴承实时工作状态。基于数据驱动的故障诊断方法能够有效利用采集数据进行诊断对象状态的监控,受限于迭代求解算法的收敛速度和精度,占用较大处理器内存资源且易在诊断计算过程中得到局部最优解[18]。为满足系统对速度传感器故障诊断的要求,本文提出一种基于迭代学习的故障诊断方法,不依靠速度传感器数学模型,基于数据驱动进行传感器故障诊断,并探究算法的收敛特性,在完成在线故障诊断功能的基础上,尽量降低运算处理器内存资源的消耗。
1 霍尔式速度传感器工作原理
图1为霍尔式速度传感器原理,其探头内部安装有永久性磁铁,当测速齿盘(导磁材料)随轴转动时会改变磁力线分布,齿顶处磁力线密集,齿根处磁力线稀疏,霍尔元件会根据此变化输出正弦信号,再通过调理电路的放大整形,输出方波信号供给采集电路。制动控制系统中多采用电流型速度传感器,即其接口信号为电源正极和电流输出信号,电流信号通过图1中采样电阻RL将电流信号转换为方波电压信号,再经过运算放大器输出频率信号。
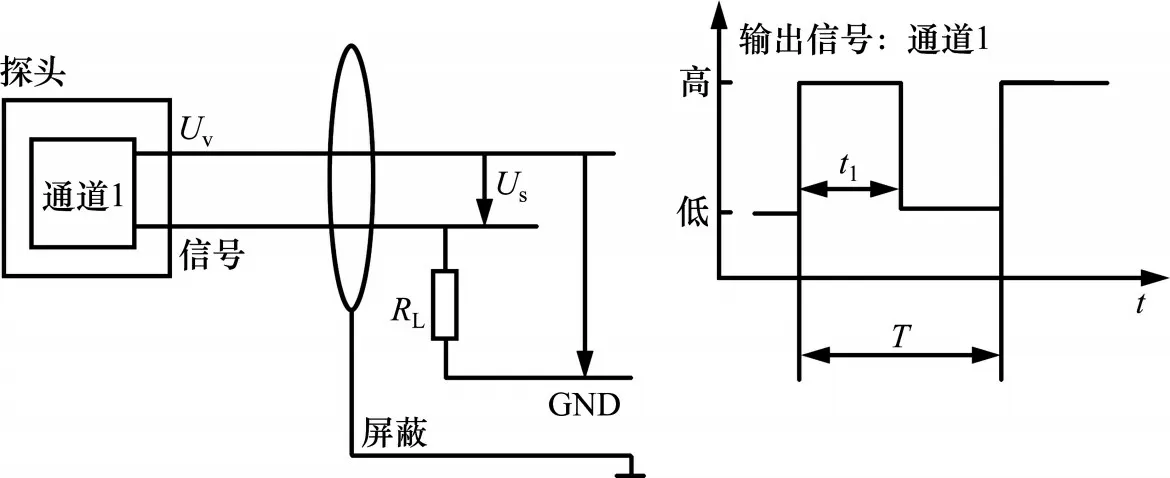
图1 霍尔式速度传感器原理Fig.1 Principle of hall speed sensor
图2 为霍尔式速度传感器信号检测电路原理,控制器中的频率采集模块通过检测单位时间内的脉冲个数确定频率量。
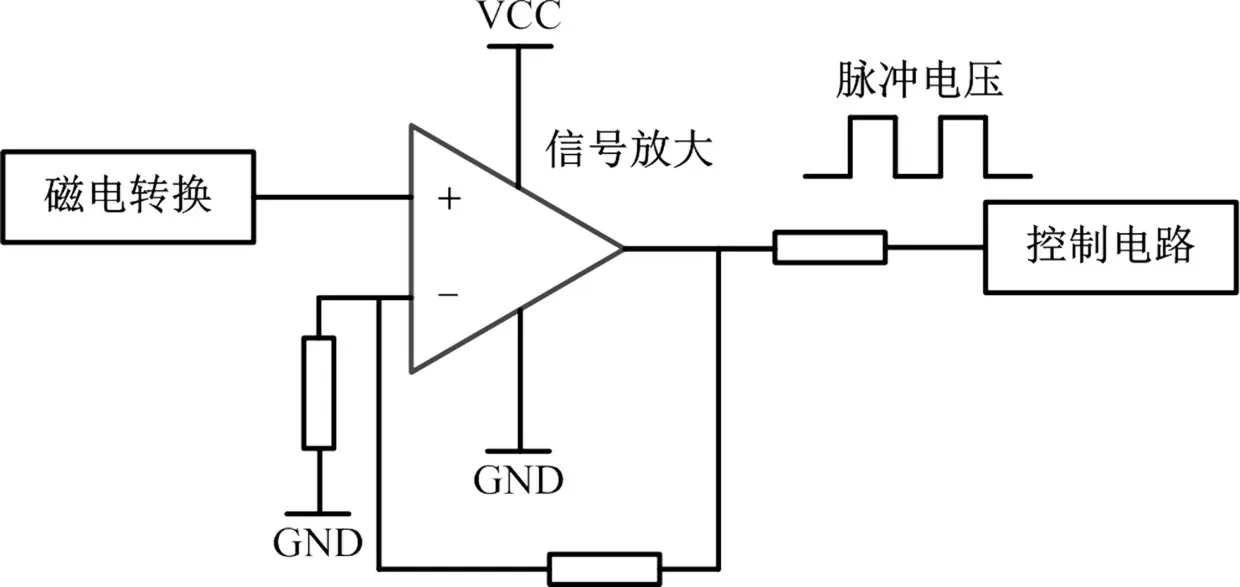
图2 霍尔式速度传感器信号检测电路原理Fig.2 Signal detection principle of hall speed sensor
再根据频率与速度转换公式即可得到轴速公式(1)。
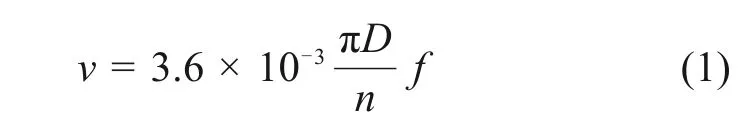
式中:v为车体运行速度,km/h;D为车轮的直径,mm;n为速度传感器齿数;f为控制器检测获取的脉冲频率。
2 迭代学习故障诊断策略
根据霍尔式速度传感器工作原理可知,其输入信号为测速齿盘齿顶和齿根引起的磁力线变化,输出信号为方波脉冲。由此可见霍尔式速度传感器可简化为线性时不变系统,考虑含有故障的线性时不变系统有
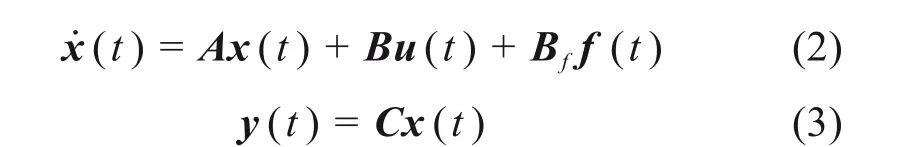
式中:x(t)为系统的状态向量;u(t)为系统的控制输入向量;y(t)为系统的输出向量;f(t)为传感器实时故障信号,此外A,B,C,Bf分别为相应维数的与系统相关的参数矩阵。图3为基于迭代学习的速度传感器故障诊断原理,其中实际过程即速度传感器实际输出,过程模型即速度传感器理论输出,定义实际过程输出与过程模型输出的差值为残差信号r(t):
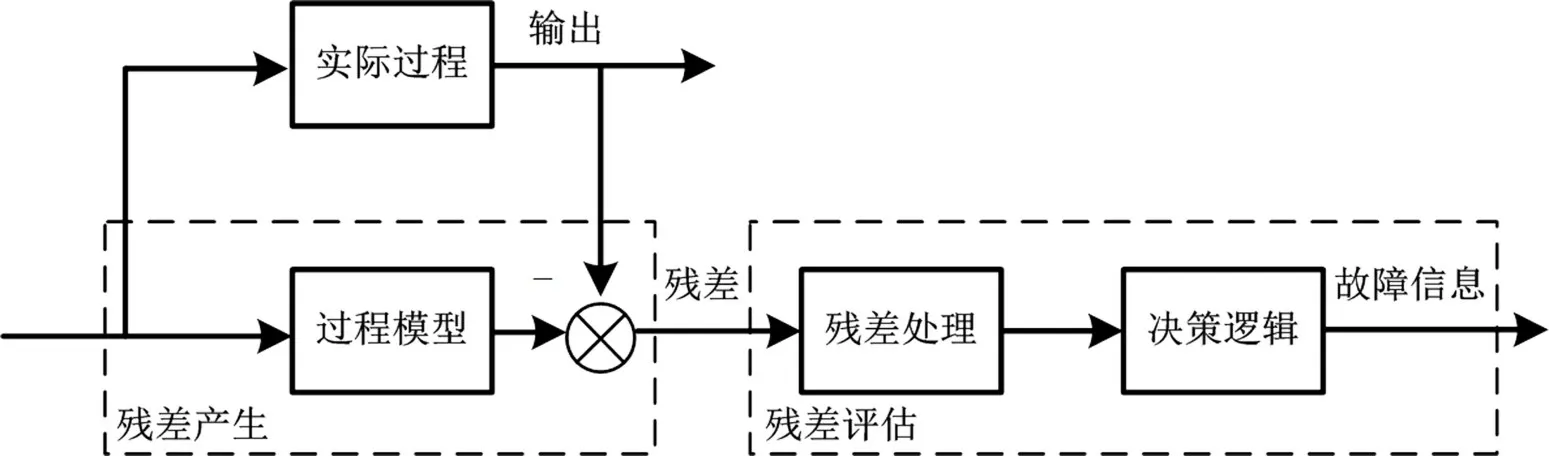
图3 基于迭代学习的速度传感器故障诊断原理Fig.3 Principle of speed sensor fault diagnosis based on iterative learning
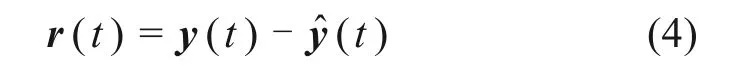
式中:残差信号为系统输出向量y(t)与系统输出估计向量y^(t)的差值,再根据残差信号和残差处理机制确定传感器实时故障信号f(t)。
为了利用系统输入输出信息准确估计故障信号,针对式(2)和式(3)的系统设计如下形式的故障跟踪器。
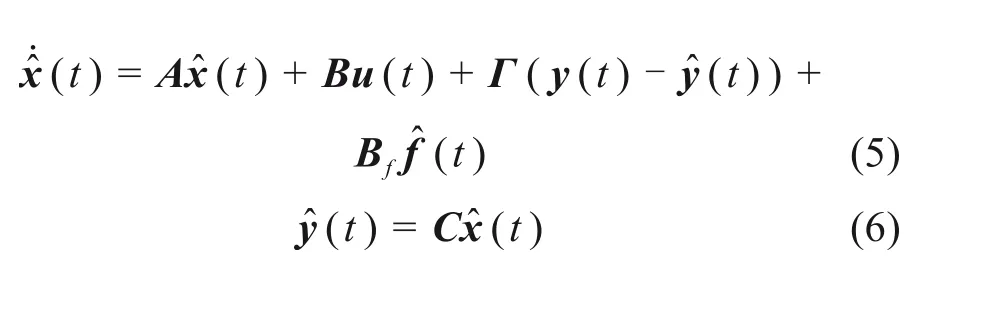

式(5)中:Γ是故障跟踪估计器的增益矩阵;L是迭代学习过程中的增益矩阵;L和Γ增益矩阵是行数与列数维度相同的对称矩阵。式(7)中的下标k代表在一个迭代学习计算过程时域区间内第k次的迭代计算。为了在有限迭代计算过程中定量描述故障,需寻找合理的学习增益矩阵使迭代学习过程在较短周期内得到最优解。为此,构建目标函数如下
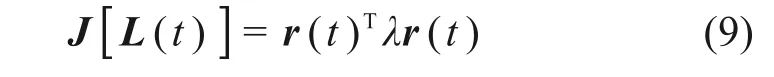
式中:λ为自定义非零正整数,根据数值分析理论可知式(9)为凸函数,在迭代计算过程中可将L和Γ初始化为单位矩阵并定义正定矩阵Q,根据共轭梯度求解算法有
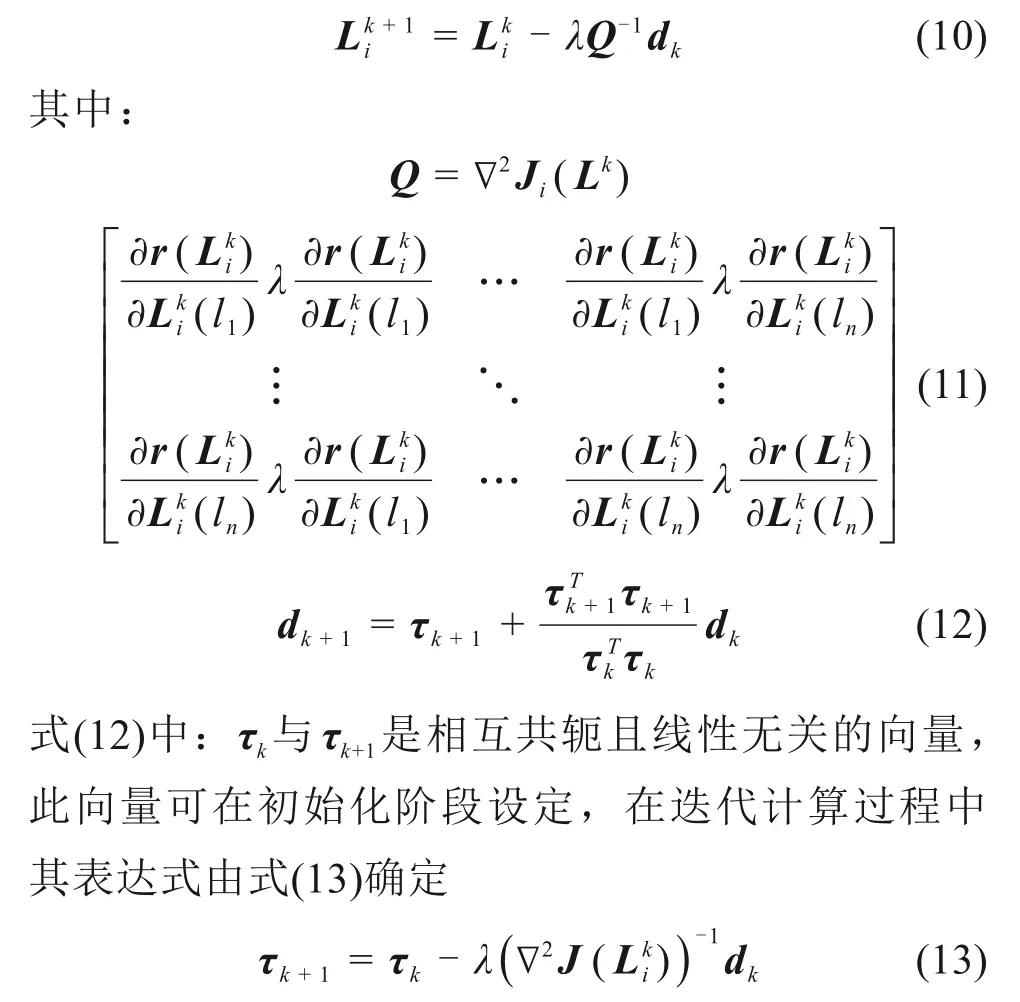
由于τk为方程求解过程中的初始化向量,在迭代中,需根据系统输出的残差信号确定,即在工程应用中可根据处理器运算能力和计算精度要求而定。
3 收敛性分析
针对第2小节的迭代学习故障诊断策略,本节将探究其算法的收敛速度和收敛精度。根据式(9)中目标函数的对称性可知其满足凸函数定义,假设式(9)满足精度要求的目标解为L0,若目标函数二阶连续可导,则有

对等式(17)两边取二范数可知,当且仅当自定义非零正整数λ满足条件0<λ<2 时,目标函数可在有限次迭代计算中收敛于最优解L0。根据式(17)可知,当λ=1时理论上目标函数可通过一次迭代实现全局收敛。然而在实际应用过程中,由于测量噪声、处理器运算精度和速度等问题,一般需通过多次迭代求得最优参数矩阵。由于所提故障诊断策略独立于A,B,C,Bf参数矩阵,且系统状态向量x(t)、系统控制输入向量u(t)及系统输出向量y(t)均可根据试验数据确定,且目标函数可收敛于最优解L0,所以利用上述过程信息可在一定时域范围内准确估计实时故障在某时域下的状态。
4 适用性分析
根据图3可知,本文所提的基于迭代学习的速度传感器故障诊断方法,就是利用实际过程和过程模型的残差信号,进行迭代学习的残差处理,再根据决策逻辑即可判断速度传感器的故障类型及可能的原因。以典型连续线性系统作为适用性验证对象[14],利用本文设计的迭代学习方法式(4)~(13),估计速度传感器中发生的实时故障式(2)中的f(t)。在验证过程中,定义初始化的故障跟踪估计器增益矩阵Γ和迭代学习过程中的增益矩阵L均为单位矩阵,4 种形式故障对应的λ增益系数为1,定义一个迭代学习优化计算过程时域区间的时间长度为5 s。假设速度传感器在工作中某时刻故障函数的数学表达式如下:


即定义的速度传感器故障主要包括指数、阶跃和正弦波3种形式,以此表征工程应用中不同故障类型,如接触不良、输出信号卡滞、输出信号震荡等。根据上述模型和边界条件,不同类型故障的估计结果如图4,每个迭代学习计算过程时域区间内实际与估计故障的误差不断减小,逼近实际故障曲线。

图4 不同类型故障的估计曲线Fig.4 Estimation curves for different types of faults
图5为基于故障估计残差的目标函数与迭代次数的关系,在初始阶段,迭代所得目标函数未能在3次迭代过程内实现全局收敛,这是由于初始化参数矩阵与最优目标矩阵参数的差异性,随着迭代次数的增加,目标函数逐渐趋于0,估计故障与实际故障的误差逐渐趋于0,迭代学习过程中的增益矩阵L逐渐趋于全局收敛。由此可见所提方法能够根据系统信息准确估计实时故障。
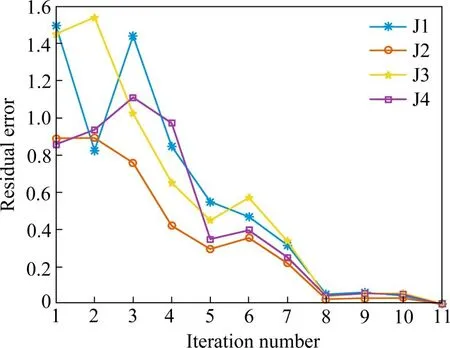
图5 基于故障估计残差的目标函数与迭代次数关系Fig.5 Relationship between objective function and iteration times based on residual error of fault estimation
5 结论
针对速度传感器的典型故障形式,本文提出一种基于迭代学习的故障诊断方法,此方法基于数据驱动,独立于速度传感器数学模型,利用迭代学习思想使估计故障不断收敛于实际故障,具有较好的收敛速度和收敛精度,为速度传感器故障诊断算法的工程应用奠定了理论基础。本文通过适用性验证证明所提方法的可用性,为扩展算法的普适性和实用性:
1) 将在此基础上增加故障模式的分类,确定更多形式的故障数学表达式,更加全面的表征速度传感器不同类型的故障。
2) 通过在嵌入式系统中试验,探究采集信号噪声及运算处理器精度对算法的收敛速度和收敛精度的影响。
3) 通过应用试验确定故障诊断过程中运算处理器对内存资源消耗,研究所提故障诊断算法在实际应用中与其他功能的兼容性。

