动态权重最大相关最小冗余算法
殷柯欣,谢爱锋,翟峻仁
(长春工业大学 计算机科学与工程学院,吉林 长春 130012)
0 引 言
在当今信息爆炸的时代,信息量呈几何倍数的速度扩充,出现了许多高维数据集。这类数据集表现出样本数量巨大、特征维度高等特点。这些出现在各个领域中的高维数据集在促进行业进步、技术发展的同时,也带来了巨大挑战。高维数据集因其庞大的样本个数和特征维度导致大量的计算资源被占用,且需要耗费海量的时间。与此同时,高维数据集中包含了大量无关和冗余的特征,这将会降低后续模型的性能。特征选择[1-2]作为一种数据预处理方式,可以很好地解决高维数据集带来的问题。由于特征选择在降低特征维度的过程中,不曾改变特征原有的物理意义,被广泛应用于文本分类[3]、数据挖掘[4]和模式识别等领域。根据与分类器结合方式不同,可以将特征选择分为包装式[5]、过滤式[6]和嵌入式[7]3类。包装式和嵌入式方法需要与分类器相结合,普适性不强,容易过拟合且计算复杂度高。相比于包装式和嵌入式方法,过滤式特征选择算法不依赖于分类器,普适性强且计算复杂度低,在高维数据集上有很强的实用性。对于过滤式方法,评价准则[8]对其显得尤为重要,它决定了所选特征的优劣。一个优秀的评价准则可以挑选出最优的特征子集。现有的评价准则可以分为距离度量、一致性度量、依赖性度量、信息度量和分类正确率5种。其中,因为信息度量[9]具有量化特征与特征,特征与类别之间的非线性关系的优点,所以信息度量一直是学者研究的热点。
基于信息度量的特征选择算法,学者们已经提出了很多,但在这些经典的算法中却少有考虑到特征之间的依赖关系。特征依赖是指具有依赖关系的单个特征似乎与类标签无关或弱相关,但当它与相互依赖的特征组合使用时,可能与类标签高度相关。好在DWFS、IWFS等算法考虑到了特征依赖,根据候选特征与已选特征的交互作用,对候选特征进行加权。然而,DWFS和IWFS这类算法过度重视特征之间的依赖关系,却忽略了候选特征与已选特征之间的冗余关系。
为了解决DWFS和IWFS存在的算法缺陷,文中提出一种名为基于交互权重的最大相关最小冗余算法(Dynamic Weight-based Maximum Relevance Minimum Redundancy Algorithm, DWMRMR)。为了验证文中算法的有效性,在5个数据集上与3种有竞争力的算法进行比较,实验表明,DIMRMR算法在大多数数据集上是优于其他算法的。
1 信息论[10]
信息熵是随机变量不确定性的信息度量。给定两个离散型随机变量X和Y。假设X=(x1,x2,…,xn),信息熵H(X)的计算公式为
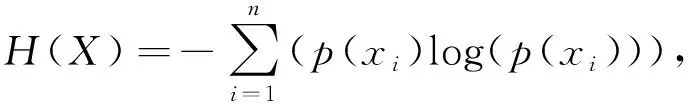
(1)
式中:p(xi)——xi的概率分布。
条件熵是已知变量Y的前提下,X中剩余的不确定性,假设Y=(y1,y2,…,yn)。条件熵H(X|Y)的表达式为

(2)
式中:p(xi,yi)——xi和yi的联合概率分布;
p(xi|yj)——xi和yi的条件概率分布。
互信息是两个变量共享的信息量。X和Y的互信息I(X;Y)的表达式为
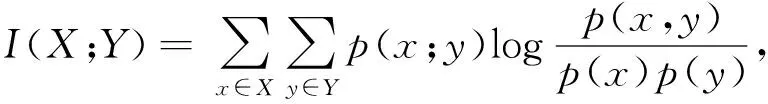
(3)
互信息、信息熵和条件熵之间的关系为
I(X;Y)=H(X)-H(X|Y)。
(4)
假设C为离散型随机变量,C=(c1,c2,…,cn)。在给定C的条件下,X和Y的条件互信息定义如下
I(X;Y|C)=H(X|Y)-H(X|Y,C)。
(5)
联合互信息是两个随机变量X和Y与变量C所共享的信息量,联合互信息I(X,Y;C)可以由条件互信息和互信息相加得到,
I(X,Y;C)=I(X;C|Y)+I(Y;C)。
(6)
2 相关工作
最大互信息算法(MIM)[11]又称为信息增益,是基于互信息最原始的特征选择方法之一,它的目标函数

(7)
式中:fi——候选特征;
F——候选特征集合;
c——类标签。
MIM计算每一个候选特征fi与标签c的互信息,按其值从大到小排列,然后按照约定选取特征。但是MIM只考虑了特征与类标签之间的相关性,却忽视了候选特征与已选特征之间存在的冗余关系。
为弥补MIM算法的不足,Battiti R[12]提出互信息特征选择算法(MIFS),
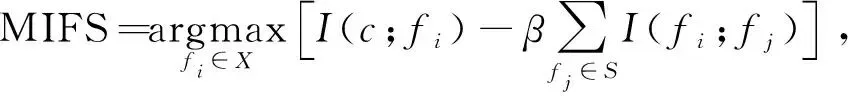
(8)
MIFS给MIM增加一个冗余项。但由于参数β是一个固定的值,MIFS的冗余项会随着已选特征数量的增加而变大,从而高估了特征之间的冗余。
2005年,Peng H等[13]提出基于最大相关最小冗余的互信息特征选择算法(MRMR),
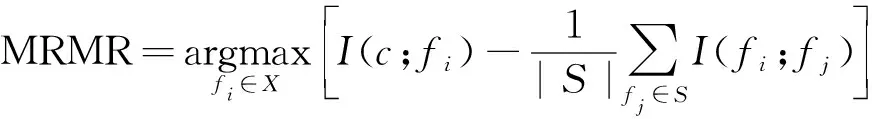
(9)

基于互信息的MIFS、MRMR等算法被认为偏向互信息值较大特征,为了解决这个问题,归一化互信息特征选择算法(NMIFS)[14]被提出,
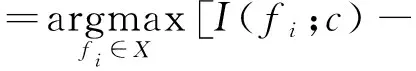
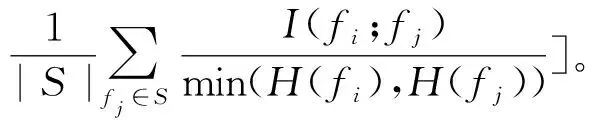
(10)
NMIFS只是MIFS改进算法中最经典的算法之一。例如,MIFS-U[15]通过在冗余项前面增加一个限制对MIFS进行改进,取得了不错的效果。将贪心算法 Non-dominated Sorting Genetic Algorithm-Ⅱ与MIFS相结合提出了名为MIFS-ND[16]的特征选择算法。
Joint Mutual Information (JMI)是基于联合互信息的特征选择算法,它在分类性能和稳定性方面表现良好,目标函数
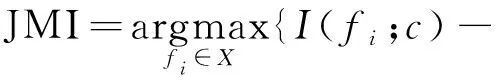
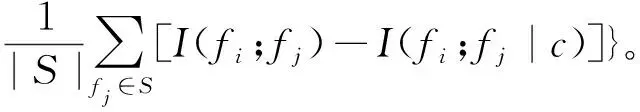
(11)
条件互信息最大化算法(CMIM)[17]将条件互信息与“maximum of the minimum”准则相结合,设计出一种不同于传统方法的算法,
与CMIM算法类似,2015年,Bennasar M等[18]提出联合互信息最大化算法(JMIM),JMIM将“maximum of the minimum”准则与联合互信息结合,解决了传统算法在使用累计求和时高估某些特征重要性的问题,

(13)
上述算法各有优点,但均忽略特征之间的依赖关系。特征依赖是指具有依赖关系的单个特征在分类任务中似乎不起作用,但如果将相互依赖的特征放在一起,将会起到更好的分类效果。为了解决这个问题,学者们提出了几个经典的特征选择算法,比如Dynamic Weighting-Based Feature Selection (DWFS)[19]、Interaction Weight Feature Selection (IWFS)[20]。
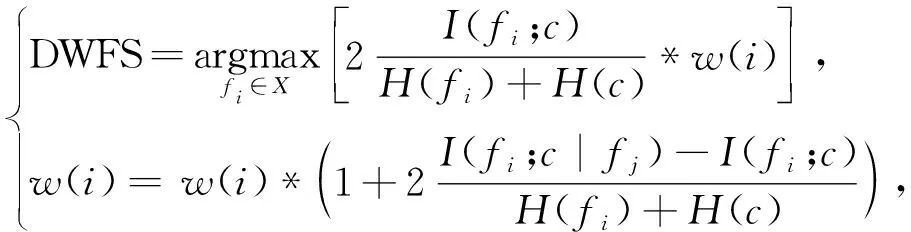
(14)
式中:w(i)——每一个候选特征的权重,初始化为1;
fj——新选中的特征。
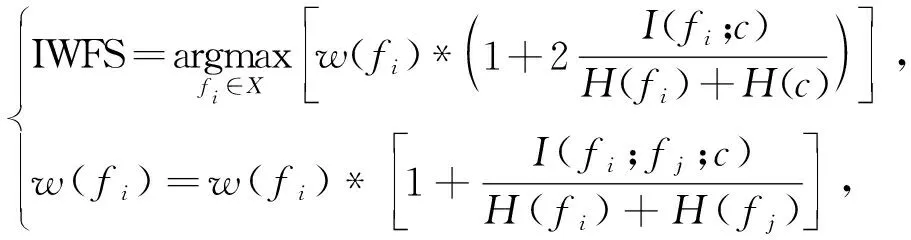
(15)
式中:w(fi)——每一个候选特征的权重,初始化为1;
fj——新选中的特征。
由DWFS和IWFS的准则函数可以看出,两者算法相似,并且存在相同的问题,文中将DWFS和IWFS归为相同的一类。虽然这类方法加快了计算速度,但只考虑到了类相关特征冗余,却忽略了特征之间的类独立特征冗余关系。
类相关特征冗余和类独立特征冗余如图1所示。
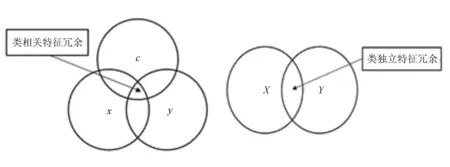
图1 类相关特征冗余和类独立特征冗余
3 算法描述
为解决DWFS这一类算法忽视特征之间冗余关系的问题,文中提出一种名为基于动态权重的最大相关最小冗余算法。
3.1 特征关系
3.1.1 特征冗余[21]
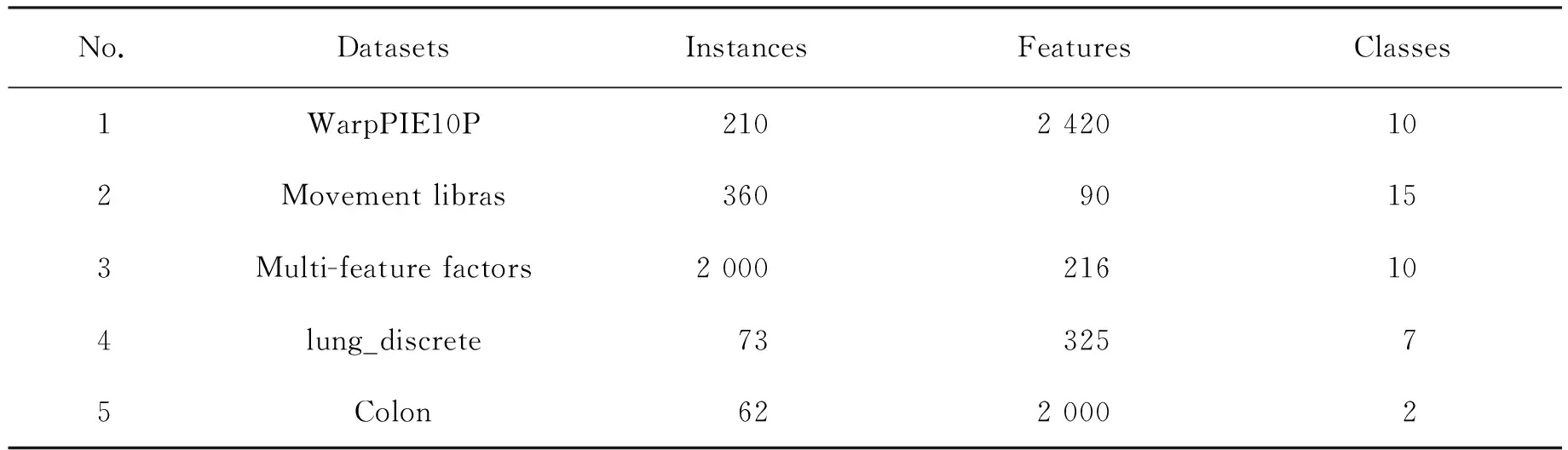
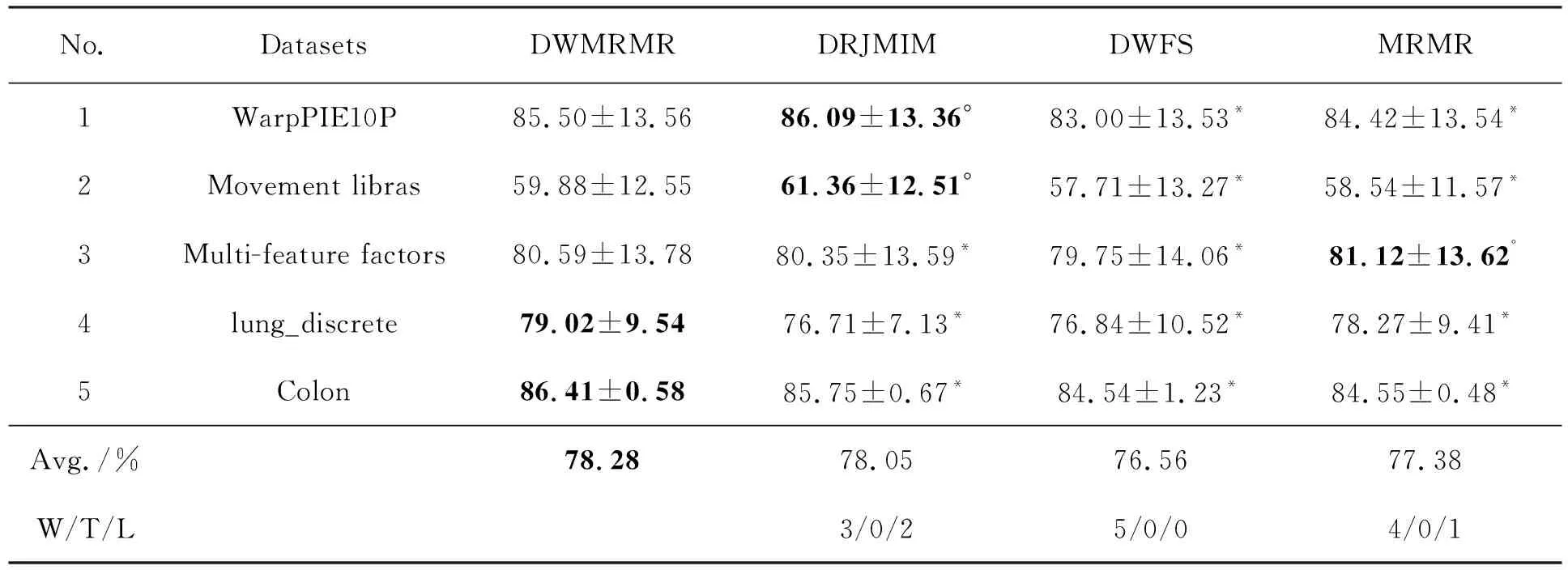
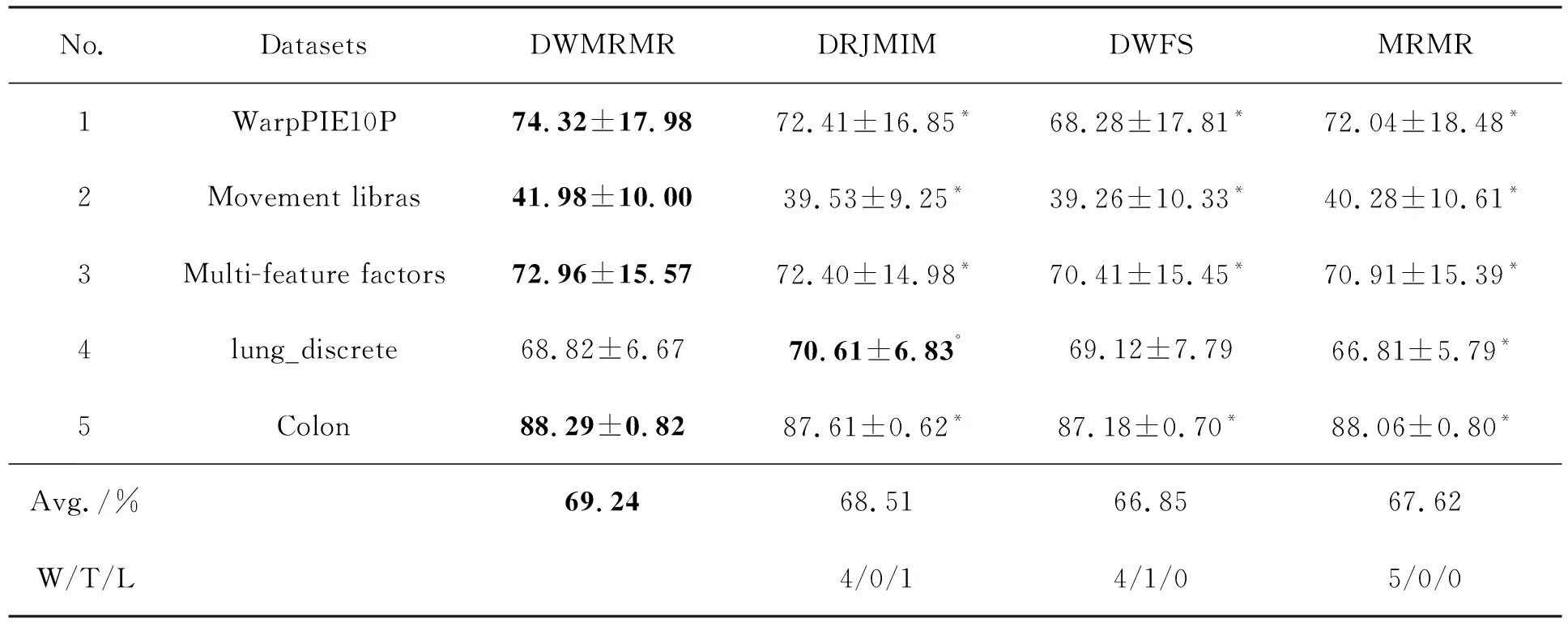
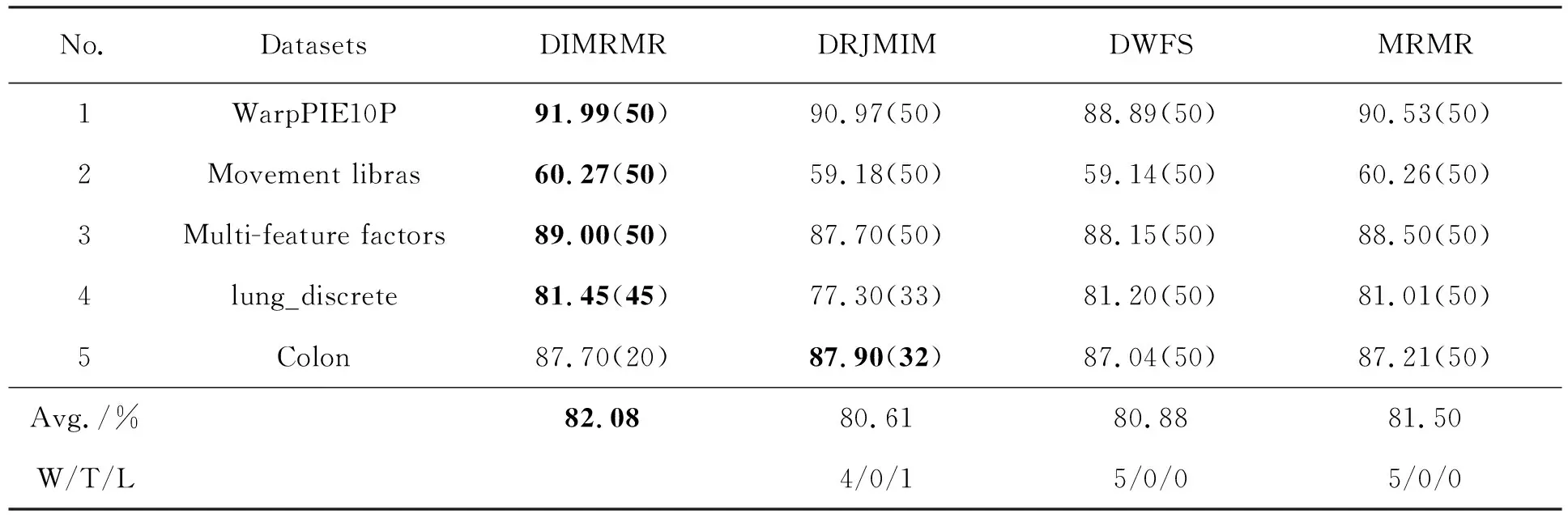
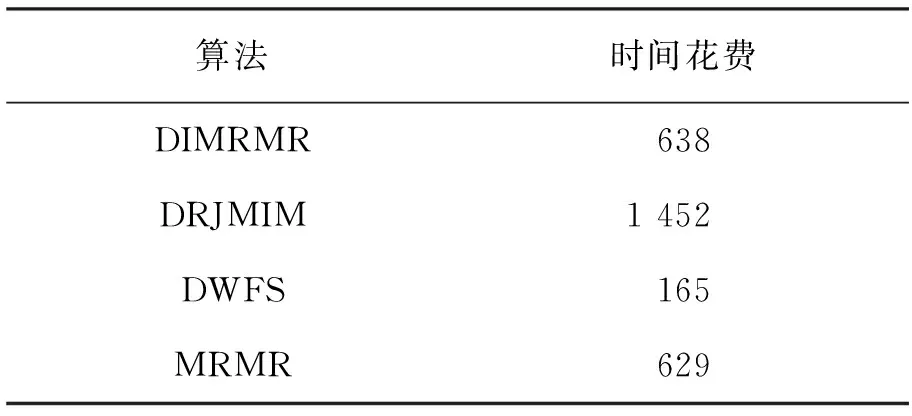
如果特征fi满足I(c;fi|Xi) 3.1.2 特征依赖 如果特征fi与类标签的相关性可以通过了解Xi得到补充,即I(c;fi|Xi)>I(c;fi),则认为fi与Xi相互依赖。 3.1.3 特征独立 如果特征fi满足I(c;fi|Xi)=I(c;fi),则认为fi与Xi彼此独立。 为了解决DWFS这一类算法忽视特征之间冗余关系的问题,文中对DWFS的准则函数进行修改, (16) DWMRMR算法1如下: Input: A training sample M with an entire features F=({f1,f2,…,fn} and the class c;User-specified threshold K. Output: selected feature subset S. 1:S=Ø,k=0 2:for i=1 to n do 3:Calculate the mutual informationI(fi;c) 4:end for 5:Initial DW(fi)=I(fi;c) for each feature; 6:while k 7:select the feature fjwith the largest DW(fi); 8:S=S∪{fj} 9:F=F-{fj} 10:or each candidate feature fi∈F do 13:Update DW(fi)=J(MRMR)*DI(fi); 14:end for 15:k=k+1 16:end while 为了验证文中算法的有效性,将该算法与3种有竞争力的特征选择算法MRMR、DWFS和DRJMIM相比较。其中,文中算法DWMRMR可分别认为是DWFS和MRMR的改进算法。 DRJMIM与DWMRMR是同类算法,且DRJMIM是最新考虑到特征依赖关系的算法。 实验环境是Inter(R)-Core(TM)i7-10750H,内存8 G,运行速度2.59 GHz,Window10-64 bit操作系统,仿真软件为PyCharm。实验过程中采用10折交叉验证方法,用10次测试结果的平均值作为最终的准确率。由于部分数据集都是连续的,实验采用CAIM[22]方法将其进行离散化[23]处理。实验中采用KNN、SVM和Native Bayes分类器构造预测模型。 实验选择了UCI通用数据集和ASU数据集,涉及医学、工程科学等领域,5个数据集包含不同的样本数、特征数和类别数,数据集的具体参数描述见表1。 表1 数据集的描述 特征选择的目的是从原始集合中选出最小的特征子集。从表1可以看出,数据集的特征维度是极高的,在特征选择中,选取数据集的全部特征是对时间和资源的极大浪费,同时毫无意义。于是,文中约定所选特征的个数限制在50以下。 平均准确率是指最优特征子集从一个特征的准确率到全部特征的准确率累加和的平均值。4种算法在3NN、SVM、NB分类器上的表现分别见表2~表4。 表2 4种算法在3NN分类器上的表现(平均准确率±标准差) 表3 4种算法在SVM分类器上的表现(平均准确率±标准差) 表4 4种算法在NB分类器上的表现(平均准确率±标准差) 对DWMRMR的分类率与其他算法进行配对双尾t检验,当P值小于5%时,认为实验结果具有显著性差异。 从表2~表4中可以看出,DWMRMR算法在KNN和NB分类器上均取得了最优表现,在SVM分类器上取得了次优表现,5种数据集在3个分类器上的Avg.值分别为78.28%、78.64%、69.24%。在表2中,DWMRMR、DRJMIM、DWFS和MRMR的Avg.值分别为78.28%、78.05%、76.56%、77.38%,DRJMIM、DWFS和MRMR分别比DWMRMR降低了0.23%、1.72%、0.9%。根据Avg.值可以得到,DWMRMR算法明显优于DWFS,且与最新算法DRJMIM相比,DWMRMR仍然表现出强劲的竞争优势。W/T/L值亦可以佐证这一点。例如在表4中,4/0/1表示DRJMIM只赢了DWMRMR算法一个数据集。4/1/0表示DWFS输给DWMRMR 4个数据集,平局一局。从5/0/0中得出MRMR输了5个数据集。 与此同时,从表2~表4可以看出,同一特征选择算法在不同的分类器上分类表现不同。比如DWMRMR算法在KNN和NB分类器上表现出最佳性能,然而在SVM上只获得了次优解。因此,分类效果与分类器是密不可分的。为了降低特定分类器对特征选择算法的影响,文中使用3个分类器的平均值表示特征选择算法的精度,如图2所示。 (a) WarpPIE10P (b) Movement libras (c) Multi-feature factors (d) lung_discrete (e) Colon 图2显示,DWMRMR算法在大多数数据集上取得了最好的分类结果,其性能明显优于MRMR、DRJMIM和DWFS。虽然在Colon数据集上,DWMRMR算法没有取得最大的分类率,但文中算法用最少的特征取得了次优解。这符合特征选择算法的目的,即选取最小的特征子集以达到最优的分类效果。为了更直观地体现特征选择算法的优劣,列出每种特征选择算法平均分类率的最大值,见表5。 表5 4种算法在每个数据集上平均分类率的最大值(最优特征子集个数) 此时的平均分类率是3种分类器的平均值。 从表5可以看出,DWMRMR算法明显优于其他3种特征选择算法,这种差距相对于DWFS表现得最为明显。根据平均分类器最大值的平均值可以看出,DWMRMR算法分别比DRJMIM、DWFS和MRMR高出1.47%、1.2%和0.58%;并且根据W/T/L,DWMRMR算法在5个数据集中,分别赢了DRJMIM、DWFS和MRMR算法4个、5个和5个数据集。由此可见,DWMRMR算法在大多数数据集上优于DRJMIM、DWFS和MRMR算法。 上述数据已经证明了DWMRMR算法分类性能的优越性。为了更加直观地展示各算法的时间花费,给出了4种特征选择算法在同一数据集上的时间花费,见表6。 表6 4种算法在Multi-feature factors数据集上的时间花费 s 由表6可知,DWMRMR算法的时间花费高于DWFS,与MRMR的时间花费几乎一样,同样明显低于DRJMIM。虽然DWFS算法的时间花费最低,但其分类表现不佳。尽管DWMRMR的时间花费不是最低,但他的分类表现却是最优的。为此,DWMRMR算法的整体性能是可以接受的。 特征选择作为一种数据预处理技术,在诸多领域得到了广泛应用。基于信息度量的过滤式特征选择算法,由于计算效率高、分类效果优异等特点被学者们大量研究。文中算法就是一种基于信息度量的过滤式特征选择算法。虽然文中算法DWMRMR改进了DWFS的分类效果,但却增加了计算时间。为此,协调时间和算法的分类性能将是下一步工作。3.2 基于动态权重的最大相关最小冗余算法(DWMRMR)
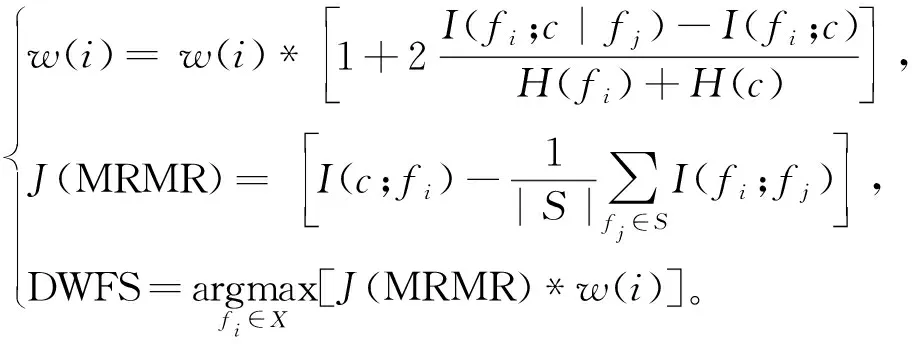
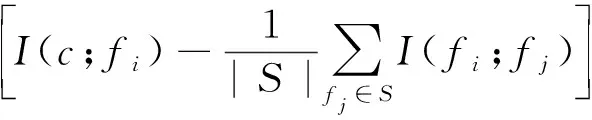
4 实验结果与分析
4.1 DWMRMR算法实验
4.2 实验结果分析




5 结 语

