篮球运动员投球命中率预测与仿真

曹 蕾，张志强

(长春工业大学 数学与统计学院，吉林 长春 130012)

0 引 言

在篮球运动项目中，投球命中率是衡量篮球运动员表现的重要指标，为篮球经理人考虑球员转会提供了参考[1]。用上赛季投球命中率预测下赛季投球命中率是直观的想法，然而James W等[2]指出,p维正态总体(协方差矩阵是单位阵)的样本均值是非容许估计[3],即收缩估计的风险函数小于极大似然估计的风险函数。同时考虑身高、体重等因素对投球命中率的影响，文中采用双水平收缩估计方法[4]对篮球运动员投球命中率进行预测，并用Matlab软件实现。

1 收缩估计方法及实现

1.1 数据结构

文中选取2017-2018赛季和2018-2019赛季篮球运动员的数据，该数据是从新浪体育中国篮球CBA专栏整理的。首先进行数据清洗：

1)2017-2018赛季和2018-2019赛季都参加的球员；

2)运动员在两个赛季投球数都大于15次，最终选取255个数据。

球员数据包括身高(x1j，cm)、体重(x2j,kg)、总篮板数(x3j)、出场数(x4j)、助攻(x5j)、抢断(x6j)、盖帽(x7j)、罚中球数(x8j)、两分球命中数(Yi1)、两分球总数(Ni1)。j=1,2分别代表2017-2018赛季和2018-2019赛季。2017-2018赛季部分球员筛选数据见表1。

表1 2017-2018赛季运动员数据

1.2 双水平收缩估计方法

2017-2018赛季共有255个篮球运动员，同时考虑一些协变量对篮球运动员投篮命中率的影响，如身高、体重、出场数、总篮板数、助攻、抢断、盖帽、罚中球数等一些协变量因素。在层次模型第二层中加入新的协变量，采用双水平收缩估计方法，但文献[4]处理的是连续型随机变量，文中数据处理的是离散型数据，要对数据进行变换。

假设

Yij～Binomial(Nij,pi),

i=1,2,…,n0,j=1,2，

式中：i——代表每一个运动员；

j——赛季，j=1代表2017-2018赛季，j=2代表2018-2019赛季；

Nij——第i个运动员第j个赛季的两分球投球总数；

Yij——第i个运动员第j个赛季的两分球投中球数；

pi——第i个运动员的命中率。

假设2017-2018赛季和2018-2019赛季的投球命中率不变，可以得到

则Xij近似分布

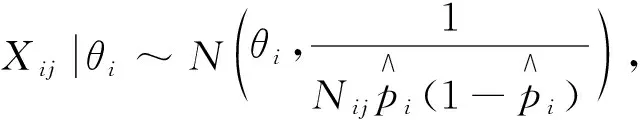
(1)

先验分布中考虑了8个协变量的因素，

θi=β0+β1x11+β2x21+…+β8x81，

β0～N(0,λ),

β1～N(0,λ),

β2～N(0,λ),

⋮

β8～N(0,λ)，

假设β0,β1,…，β8都独立。j=1代表2017-2018赛季数据，文中用2017-2018赛季数据来预测2018-2019赛季的投球命中率。其中x11，x21，…，x81分别代表第1个赛季的身高、体重、总篮板数、出场数、助攻、抢断、盖帽、罚中球数，则

收缩估计是

(2)

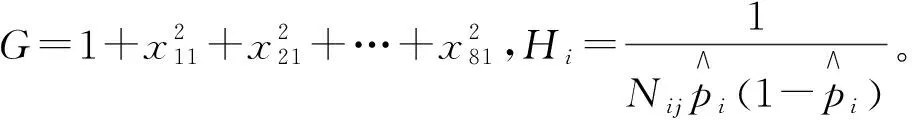
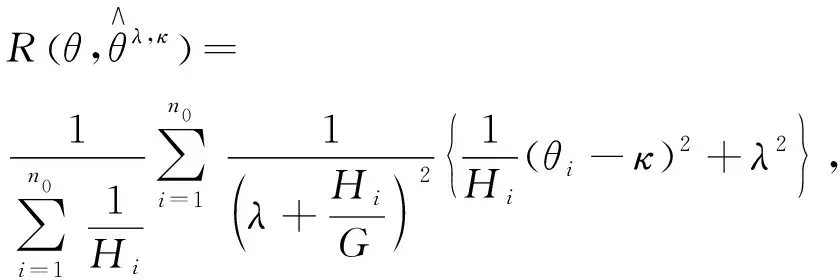
(3)

风险函数式(3)的无偏估计为

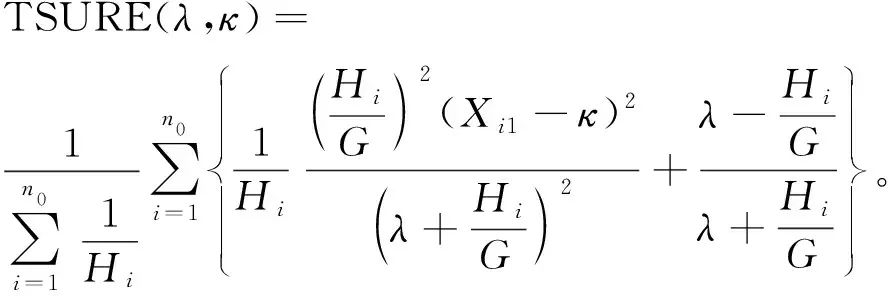
(4)

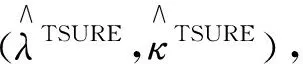
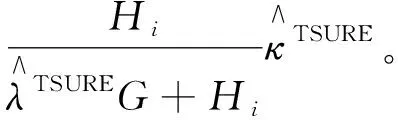
(5)

1.3 风险函数无偏估计最小化的Maltab实现

对风险函数无偏估计式(4)通过Matlab实现[5-7]，考虑后卫、前锋、中锋和全体篮球运动员,以全体篮球运动员数据为例进行编程。具体流程如图1所示。

具体编程如下：

CBA1=xlsread('18zongti.xlsx');%导入数据集

p=CBA1(:,1)./CBA1(:,2);%极大似然估计

H=1./(CBA1(:,2).*p.*(1-p));

X=log(CBA1(:,1)./(CBA1(:,2)-CBA1(:,1)));

G=1+((CBA1(:,3)-mean(CBA1(:,3)))./std(CBA1(:,3))).^2+((CBA1(:,4)-mean(CBA1(:,4)))./std(CBA1(:,4))).^2+((CBA1(:,5)-mean(CBA1(:,5)))./std(CBA1(:,5))).^2+((CBA1(:,6)-mean(CBA1(:,6)))./std(CBA1(:,6))).^2+((CBA1(:,7)-mean(CBA1(:,7)))./std(CBA1(:,7))).^2+((CBA1(:,8)-mean(CBA1(:,8)))./std(CBA1(:,8))).^2+((CBA1(:,9)-mean(CBA1(:,9)))./std(CBA1(:,9))).^2+((CBA1(:,10)-mean(CBA1(:,10)))./std(CBA1(:,10))).^2;

h=H./G;

q=1./H;

程序中p表示球员赛季命中率，H表示Xi1的近似方差，X表示变换后的连续性数据。x11,x21,…,x81的单位是不同的，所以对x11,x21,…,x81进行了单位化。CBA1(:,3)代表身高，CBA1(:,4)代表体重，CBA1(:,5)代表出场数，CBA1(:,6)代表总篮板数，CBA1(:,7)代表助攻，CBA1(:,8)代表抢断，CBA1(:9)代表盖帽，CBA1(:,10)代表罚中球数，所以G也需要相应的单位化，即

式中：std——标准差。

lamda0=var(X);

x0=[20 100];

L=length(G);

global G H lamda0 L;

camel= @(x,y) 1./(sum(q)).*(sum((q.*(h.^2.*(X-x).^2))./((y+h).^2)+(y-h)./(y+h)));

loss=@(xo_sa) camel(xo_sa(1),xo_sa(2));

options1 = struct(...

'CoolSched',@(T) (.95*T),...

'InitTemp',10^7,...

'MaxConsRej',10^5,...

'MaxSuccess',10^4,...

'MaxTries',10^5,...

'StopVal',10^(-5),...

'Verbosity',1);

[xo_sa,fo_sa]=anneal1(loss,x0,options1);

这部分程序的任务是最小化风险函数的无偏估计，从而得到超参数的估计。风险函数的无偏估计是一个非常复杂的函数，采用梯度的最优算法和Nelder算法[8]无法实现式(4)的最小化，所以采用模拟退火[9-10]方法进行最小化。

anneal1是模拟退火程序。鉴于篇幅原因，文中不展示模拟退火程序。

得到超参数的估计后，根据式(5)得到收缩估计。为了评价收缩估计方法的好坏，采用预测误差(WPE),

SURE收缩估计方法[11]文中也是采取加权平方损失函数。因此可以根据WPE的大小来判断双水平收缩估计和SURE收缩估计的好坏，WPE越小，收缩估计越精准。

2 结果分析

数据经过预处理后，文中认为身高、体重、出场数、总篮板数、助攻、抢断、盖帽、罚中球数这些协变量与命中率密切相关。按照位置不同，考虑后卫、前锋、中锋和所有球员的两分球命中率。WPE结果见表3。

表3 WPE结果对比

从表3可以得出结论，即考虑协变量对预测误差改善是有帮助的。双水平收缩估计方法考虑了协变量，SURE收缩估计方法没有考虑协变量，对于后卫、前锋、中锋、所有球员，双水平收缩估计方法的WPE都小于SURE方法的WPE。

3 结 语

根据2017-2018赛季数据预测2018-2019赛季投球命中率，采用双水平收缩估计方法和SURE收缩估计方法[11]进行预测。双水平收缩估计方法是处理连续随机变量，而投球数是离散型数据，进行变换后得到连续型变量。最小风险函数的无偏估计是比较有挑战的工作，因为常用梯度的最优算法和Nelder算法无法实现式(4)的最小化，所以采用模拟退火方法实现风险函数无偏估计的最小化。因为双水平收缩估计方法的WPE小于SURE收缩估计方法的WPE，所以双水平收缩估计方法比SURE收缩估计方法好。SURE收缩估计方法没有双水平收缩估计方法好的原因是SURE收缩估计方法没有考虑协变量因素(身高、体重等)。

综上所述，文中对2018-2019赛季篮球运动员数据进行分析，对投球命中率进行预测，双水平收缩估计方法的预测误差非常小，希望对篮球运动员转会提供一定的参考作用。