水平集曲率引导的卡通-纹理图像分解①

尚婉清，许建楼，郭雨莹

(河南科技大学数学与统计学院, 河南 洛阳 471023)

0 引 言

图像分解是图像处理和计算机视觉领域一项基础且重要的研究方向，它在目标识别[1]、生物医学[2]、深度学习[3,4]等领域都有广泛的应用。在图像的结构-纹理分解模型中，通常用不同的函数空间刻画结构和纹理部分。常用来刻画图像结构部分的TV正则项虽然能够去除图像均匀区域的震荡成分，但也会磨光边缘和拐角等细节特征。水平集曲率从图像的局部几何结构出发，分析图像中某一点的水平集曲线和梯度的联系，在保证结构图像正则性的前提下，处理小尺度的边缘细节。由于图像强度乘以一个正的常数不影响图像的水平集，因此图像的水平集曲率作为一个常数矩阵加入到正则项中是对比不变的。此外，纹理震荡成分常用H-1泛函度量，然而现有的使用H-1泛函的模型在求解过程中都忽略了Hodge分解得到的零散度向量函数。从数学上看，被忽略的向量函数包含一定的向量信息，而这些信息能够扰动纹理，进而影响分解结果。于是提出了带有零散度向量场约束的结构纹理分解模型，然后利用交替方向法求解模型。在数值实验中对比分解效果和纹理的向量信息发现，与其他几个变分模型的实验相比，提出的改进模型有较好的效果。

1 模型准备

1.1 OSV模型

Vese, Osher和Sole[5]提出的分解模型是图像分解中一个广泛应用的变分模型，简称OSV模型如式(1)：

(1)

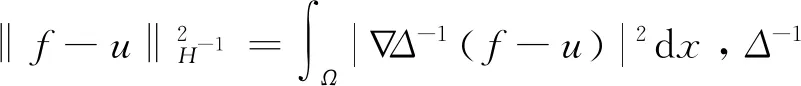
图1 零散度向量q对g的影响

1.2 水平集曲率

对一个给定的图像f，沿着边缘方向的像素点变化平缓，因此梯度较小，垂直边缘方向的像素点变化剧烈，对应的梯度也较大。然而在图像的拐角处，梯度曲率差距非常大，这使得普通的TV正则项不能很好的处理图像拐角，具体的推演证明可以在文献[6]中找到。文献[6]提出模型如式(2)：

(2)

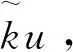
k(f)=div(∇f/|∇f|)

(3)

应用低通滤波器得到的。

2 本文模型及算法

2.1 新模型

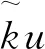
(4)

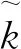
2.2 模型算法

交替乘子方向法(ADMM)[7]是一种用于求解具有可分结构的约束优化问题的重要算法。该算法具有处理速度快，收敛性能好等优点。通过引入三个辅助变量，将模型(4)化为约束最小化问题，然后利用交替方向法计算。

首先引入三个辅助变量ω,p,g，令ω=∇u,p=Δ-1(f-u),g=∇p+q，式(4)可以改写为以下约束最小化问题如式(5)：

(5)

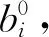
(6)

(7)

(8)

(9)

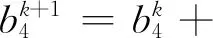
(10)

对最小化问题(6)，给定初始值ω0,u0,p0,q0,g0，应用交替乘子方向法，迭代k步，然后通过以下公式更新ωk+1,uk+1,pk+1,qk+1,gk+1如式(11)-式(15)：

(11)

(12)

(13)

(14)

(15)

对ω-子问题，可以通过软阈值函数得到其精确解：

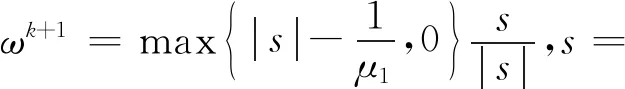
(16)

对u-子问题, 它的Euler-Lagrange方程可用直接变分法求得:

(17)

其中，∇T是∇的伴随算子，且满足∇T=-div，如果对散度算子利用周期边界条件，则可以通过快速傅里叶变换(FFT)求解。

类似的，对q-子问题，可以得到下面对应的Euler-Lagrange方程并用FFT求解：

(18)

对p-子问题，先变分得到如下Euler-Lagrange方程再用FFT求解：

(19)

对g-子问题，根据L1优化的特征，可以用软阈值函数求解:

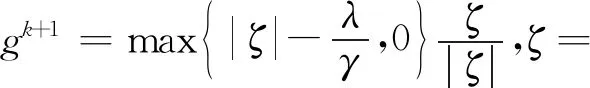
(20)

3 实验分析

3.1 参数设置

模型的仿真在MATLAB中执行，令δ=10-3，迭代停止条件设置为：

首先归一化测试图像f，然后将辅助变量ω,z,g初始化为ω0=f,z0=0,g0=0。设置Butterworth低通滤波器的阶数为10，截断频率b=40。实验发现，对参数λ,γ，当γ≤1时，λ越小结构越光滑，而λ越大纹理脸部提取越干净。当固定λ=0.6,μ1=1.5,μ3=0.5,γ=0.8时，参数μ2≤3时都可以达到很好的分解效果。迭代次数设为150次。

测试图像如图2所示，从左到右分别是Barbara 256图像、合成图像、Barbara 512图像。

(a)

3.2 实验结果

对以上测试图像仿真实验来验证新模型的可行性和有效性。参与实验的其他模型主要有OSV模型以及使用了H-1泛函的模型[8](以下简称NNTV-H-1模型)。每个模型均通过人工调整参数达到最好的分解效果。在实验中通过展示纹理图像的向量场直观的说明新模型的创新点。下面展示三个模型对测试图像的实验结果。图3是Barbara 256图像在三个模型上的分解结果，其纹理对应的向量场在图5展示，并给出了新模型中零散度向量函数q的向量场。

图6列出了Barbara 512图像的分解效果。

(a) OSV

(a) OSV

(a) OSV

(a) OSV

从图3-6能够很容易的观察到以下几点：

1) 新模型分解Barbara纹理图像的脸部能够很好的分离出来，其他两个模型则稍显逊色。观察图4发现，新模型分解的结构保持边缘的能力更优，拐角处边缘清晰。

2) 以上的纹理向量场图像反映出忽略q对纹理信息造成明显的干扰，具体表现在与本文模型相比，忽略q的模型所得纹理向量场背景部分有杂乱的向量信息。

3)q向量场是包含许多向量信息的，在q向量场的作用下，纹理信息的线条纹路更清晰，这是由于q的向量方向与∇z的向量方向相互抵消或合并的效果。

4 结 语

提出了一个新的曲率引导的带有零散度向量场约束的图像结构纹理分解模型。将水平集曲率加入模型正则项并用低通滤波器处理高频信息；对大量使用的H-1泛函进行改进，保留了经常忽略的向量函数q；最后结合增广拉格朗日乘子法和交替方向法求解提出的模型。在实验中将纹理对应的向量场及零散度向量函数的向量信息直观的展示出来并分析了其对纹理的影响。实验结果表明，改进的模型保持结构图像的边缘和拐角的能力明显提高，纹理提取更彻底，且无论从理论上还是实际表现上，向量信息都更加完整。