基于PSO-SVR的电力负荷预测①

胡永迅，李彦梅

(1.安徽理工大学电气与信息工程学院，安徽 淮南 232001;2.安庆师范大学电子工程与智能制造学院，安徽 安庆 246133)

0 引 言

电力负荷科学准确的预测不但可以节约能源，而且能促进节能减排工作的顺利完成。精准的负荷预测在电力系统稳定运行中起着较为重要的作用，可以为电力公司制定工作计划、能源的供给提供重要的参考信息。目前国内外科研学者提出了多种多样的关于负荷预测的方法与理论。经典的负荷预测多以统计学为基础，例如指数平滑法、回归分析法[1]。然而随着大量的方法不断地诞生，预测结果的精度仍然有待进一步提高。基于此现状，引入了人工智能领域中经典的智能进化算法优化经典预测模型的重要参数，进而提高了预测精度。提出的优化模型具有能够自学习、自组织、自适应的优良等特征。优化后的预测模型拥有简单通用、鲁棒性强、适应面广等一系列优点。支持向量回归机的预测精度主要取决于其惩罚因子和核函数参数，利用遗传优化算法、人工蜂群优化算法和人工蚁群算法等智能算法对参数寻优极大提高了模型的预测精度[2]。采用应用较为广泛的粒子群算法优化SVR参数，提出了粒子群算法优化支持向量机回归(Particle Swarm Optimization Support Vector Regression,PSO-SVR)的负荷预测模型，提高了预测精度，取得了理想的预测结果。

1 PSO优化SVR模型

1.1 支持向量机回归

SVM是一种源于统计学，新的机器学习方法。支持向量机回归(Support Vector Regression,SVR)是在SVM的基础上引入ε不敏感损失函数而形成的。它的核心思想是得到让所有样本距离分类面误差最小的最优分类面[3]。

现令训练样本为(xi,yi)∈Rn×R,xi为输入自变量，yi为输出因变量，n=1,2,3,…,l，l代表输入特征数据xi=(环境温度、节假日、工作日、日期)的总个数。线性回归函数表达式为式(1)：

f(x)=ωΦ(x)+b

(1)

式(1)中Φ(x)为映射函数；ω代表权重；b代表偏差。

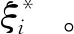
(2)

式(2)中C为惩罚因子，ε代表回归函数的误差大小。

为了解决非线性回归的问题，用核函数将低维非线性输入样本转化为高维空间求出回归函数如式(3)。

(3)

选择的核函数为径向基核函数如式(4)。

(4)

1.2 粒子群算法

1995年，美国科学家James Kennedy和 Russell Eberhart联合提出了粒子群算法(Particle Swarm Optimization,PSO)。该算法具有原理简明易懂、实现起来比较方便，收敛速度比较快、需要设置的参数较少等一系列优点的进化算法，而被广泛应用[4]。

粒子群算法的起源是模仿自然界中的鸟类寻找食物的过程。每只鸟都象征着问题的一个解，称为粒子。每个粒子的速度取决于它们搜寻的方向和距离[5]。种群中适应度最好的粒子会受到所有粒子的追随[6]。在不断迭代搜索最优解的过程中，每一次迭代粒子都通过两个极值来不断更新自己的速度和位置[7]。分别是个体极值和全局极值，个体极值是粒子自身搜索到的最优解[8]，全局极值就是整个粒子群当前搜索找到的最优解[9]。

假设在D维的搜索空间内，一个种群包含N个粒子，第i个粒子是一个D维向量：

Xi=(xi1,xi2,…,xiD),i=1,2,…,N

第i个粒子的速度是一个D维向量：

Vi=(vi1,vi2,…,viD),i=1,2,…,N

第i个粒子当前搜索到的个体最优解记为个体极值：

Pbest=(pi1,pi2,…,piD),i=1,2,…,N

整个粒子群当前找到的全局最优解记为全局极值：

gbest=(pg1,pg2,…,pgD)

找到两个极值点后，粒子通过下面的公式(5)，(6)来更新速度和位置：

Vid=ω·vid+c1r1(pid-xid)+c2r2(pgd-xid)

(5)

xid=xid+vid

(6)

式中c1和c2为加速常数，也叫学习因子；r1和r2为[0，1]之间的随机数。

2 粒子群算法优化支持向量机的回归

粒子群算法是一种广泛应用于各个领域的智能优化进化算法，它具有搜索覆盖范围大、收敛速度特别快、精度非常高等特点[10]。而且算法本身需要设置的参数少、比较容易实现的特点而被广泛应用。因此选用PSO算法去进行SVR参数的优化选择。首先设置优化模型的相关参数：种群的大小设定为15，惯性权重设为8，设定学习因子c1和c2的值为1，最大进化代数设定为60，同时还设定了速度和位置的变化范围。紧接着进行适应度计算，本文的适应度函数为均方误差。然后更新个体最优值，迭代之后计算得到的目前适应度值与之前的历史最佳值相比较，若当前适应度值更满足评价标准则取而代之，若不符合则不做改变。紧接着更新全局最优值：每次迭代之后比较所有粒子的个体最佳值，把最符合评价标准的那个值取出与目前全局最佳值作比较，若更加符合则取而代之，否则不做改变。接着进行速度与位置更新，对当前组合的位置和速度进行调整。然后判断是否满足终止条件。当满足条件时，则迭代终止，否则返回。最后将参数C和g的最优值构建电力负荷预测优化模型进行预测。

3 模型的应用与评价

3.1 数据来源与评价指标

实例选取某地区一年的环境温度、节假日、工作日、日期和负荷数据。每30min采集一次负荷数据，一天共采集48次，然后计算得出日平均负荷作为模型的输出。选取前11月的数据作为训练样本，12月份的数据作为预测样本。选择均方误差、均方根误差、平均相对误差、平均绝对误差和决定系数这五大指标对模型预测结果进行评价。

均方误差(MSE),如公式(7)：

(7)

均方根误差(RMSE)，如公式(8)：

(8)

平均相对误差(MRE)，如公式(9)：

(9)

平均绝对误差(MAE)，如公式(10)：

(10)

决定系数(R2)，如公式(11)：

(11)

3.2 结果分析

为了验证基于PSO-SVR的电力负荷预测方法的高准确性，将该预测方法和优化前的方法以及BP神经网络方法做对比。其结果如图1所示，通过图像可以明显看出本文模型的预测结果拟合最好。

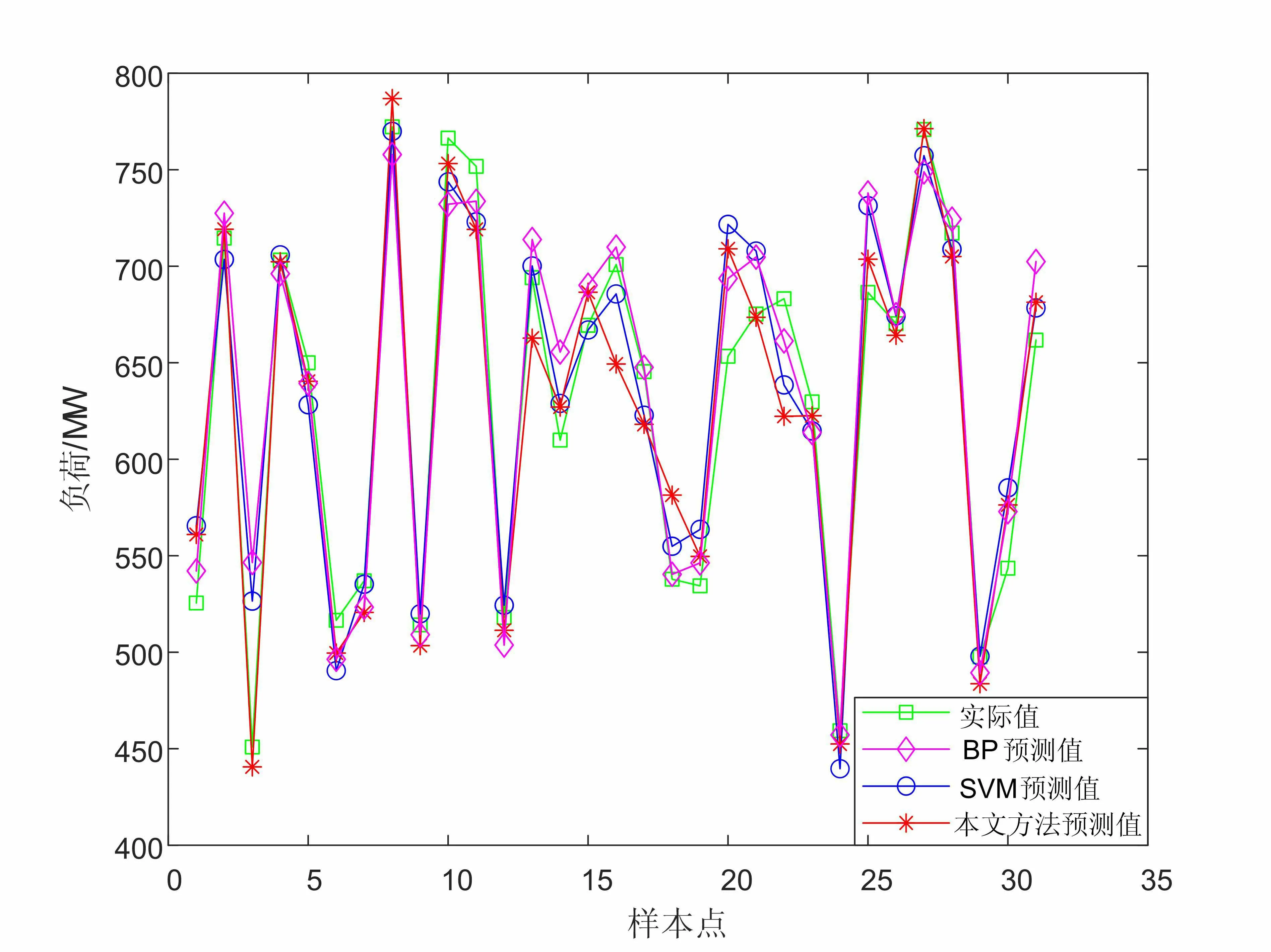
图1 预测结果对比图

3.3 误差分析

由于相对误差可以较好的反映预测结果的准确性，所以输出了三种方法的相对误差对比图如图2，通过图形可以直观得观察到优化后降低了误差。预测结果误差对比如表1，通过对比可以发现，优化后的最大相对误差从16.77%降为8.92%，缩小了误差变化的范围。通过表2可见预测方法的各项误差最小，取得了最理想的预测结果。

图2 相对误差对比图

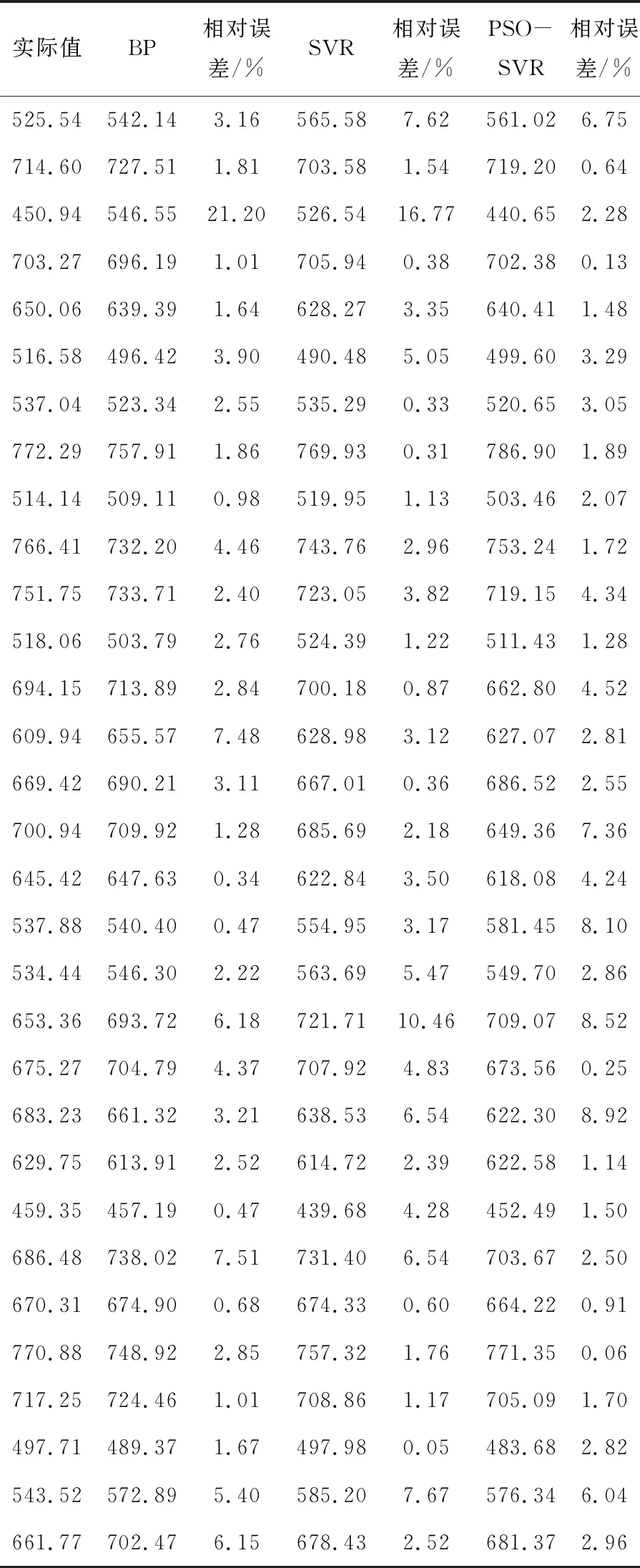
表1 预测模型预测值与实际值

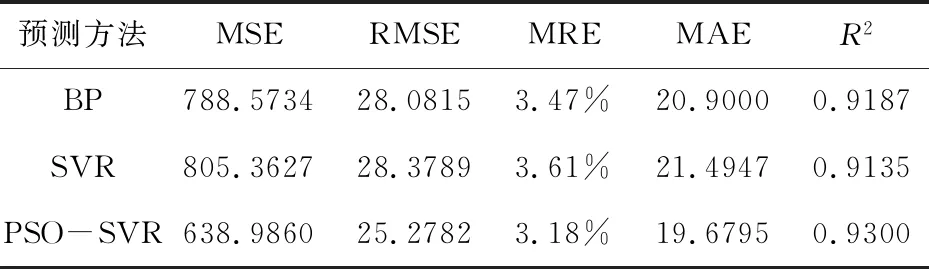
表2 预测结果误差对比

4 结 语

通过SVR对电力系统负荷预测时，惩罚因子C和核函数参数g是随机初始化为某一区间的随机数。参数的选择对网络预测的结果影响非常大，不同C和g的选择会导致预测结果的精度不为不同。为了提高网络的预测精度，提出一种基于PSO-SVR的电力负荷预测方法，以均方差为适应度函数，迭代寻找到最佳的C为0.1153和最佳的g为6.4249。通过优化降低了电力负荷预测的误差，提高了预测的精度。