一种耦合电感双倍压单元高增益Boost 变换器

刘 洋，董锋斌，皇金锋

（陕西理工大学电气工程学院，汉中 723001）

近年来，随着技术水平不断进步，能源消耗也越来越大，导致传统化石燃料和能源陷入危机，高效利用新能源极为重要[1-2]。其中，风能、光伏电池和燃料电池引起了广泛关注，但是都存在输出电压低而不能直接逆变并网的问题，而解决问题的有效途径是通过高增益DC/DC 变换器来实现电压提升，以此达到并网逆变所需的电压[3-5]。

在传统的Boost 变换器中，理论分析表明，电压增益可以是无限的，但在实际使用中，会存在几个比较严重的问题，如二极管反向恢复、器件电压应力高、损耗大，由于器件寄生参数的存在，甚至会出现电压增益与占空比负相关的情况，无法满足输出电压范围宽的要求[6]。因此，国内外学者对于高增益DC/DC 变换器进行了广泛研究。文献[7-9]使用级联的办法来得到更高的电压增益，但级联会造成后级功率器件电压应力大，对器件要求高，依旧有二极管反向恢复等问题；文献[10-11]通过开关电容（电感）单元倍压，电压增益得到了显著的提升，但缺点是电路构造复杂、器件数目多、灵活性差、成本高。耦合电感型高增益变换器通过将2 个及以上的电感集成在一起的方式，不仅减小了变换器的体积，而且电压增益可以通过一个新的变量（耦合电感的匝数比）来控制，使其电路结构更简单，成本更低，因此，国内外很多学者对耦合电感型高增益变换器进行了研究[12-14]，但由于漏感的存在，造成电路谐振，产生电压尖峰，使得系统效率降低。为此，针对其不足之处就需要做出准确改进来优化变换器的性能。

本文提出的变换器是通过将2 组倍压单元与耦合电感的结合方式来吸收漏感能量，有效解决功率器件两端电压尖峰与电压应力大的问题，从而优化变换器性能。将从变换器的工作原理及稳态性能两方面进行分析，通过实验平台制作一台100 W 的模型，验证理论分析的正确性。

1 电路结构与工作原理分析

1.1 拓扑提出

本文所提高增益变换器电路拓扑及其等效电路如图1 所示。为了更好地分析电路的工作情况，需要将原电路进行等效变换，其等效电路如图1（b）所示，将耦合电感的原边等效出2 个电感量：励磁电感Lm和漏感Lk。电容C1-二极管D1支路可以吸收原边漏感的能量，避免了与开关管谐振。电容C2和C3、二极管D2和D3以及耦合电感线圈n2组成桥式倍压单元，通过电容C2和C3分别储能后一同放电，以达到更高增益的目的。设耦合电感匝数比N=n2∶n1，耦合系数k=Lm/（Lm+Lk）。

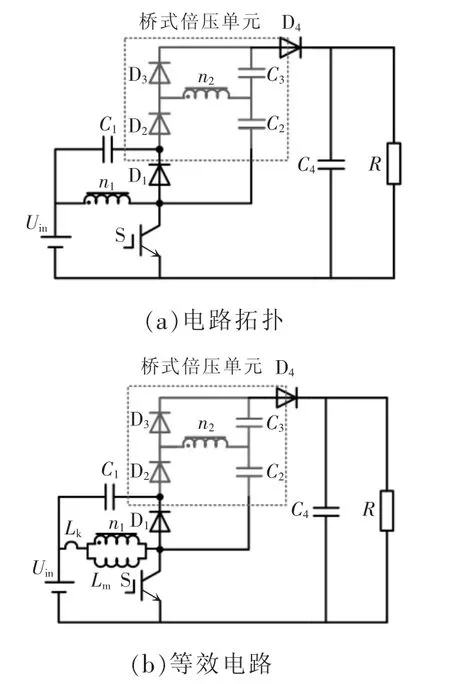
图1 高增益变换器电路拓扑及其等效电路Fig.1 Circuit topology of high-gain converter and its equivalence

1.2 变换器的工作原理

自开关管S 导通到下一次导通期间一共存在5 种工作模态，如图2 所示。开关管以及二极管各模态的状态如表1 所示。变换器稳态工作时的主要波形如图3 所示。

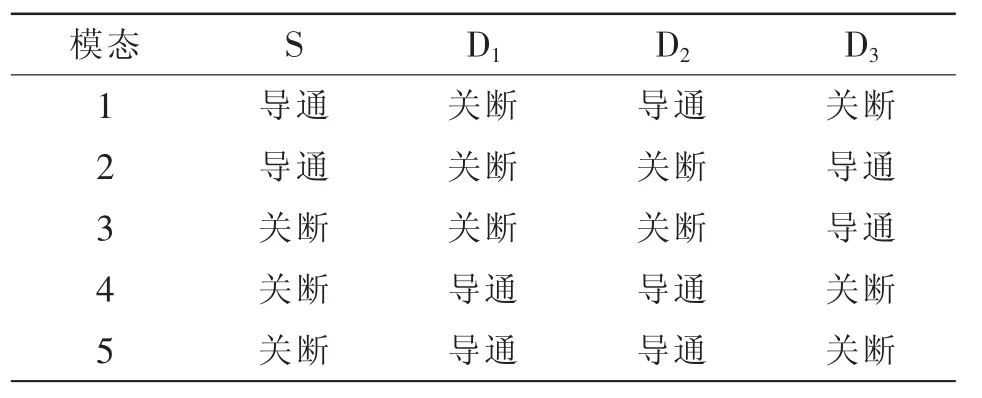
表1 开关管及二极管状态Tab.1 Statuses of switch tube and diodes

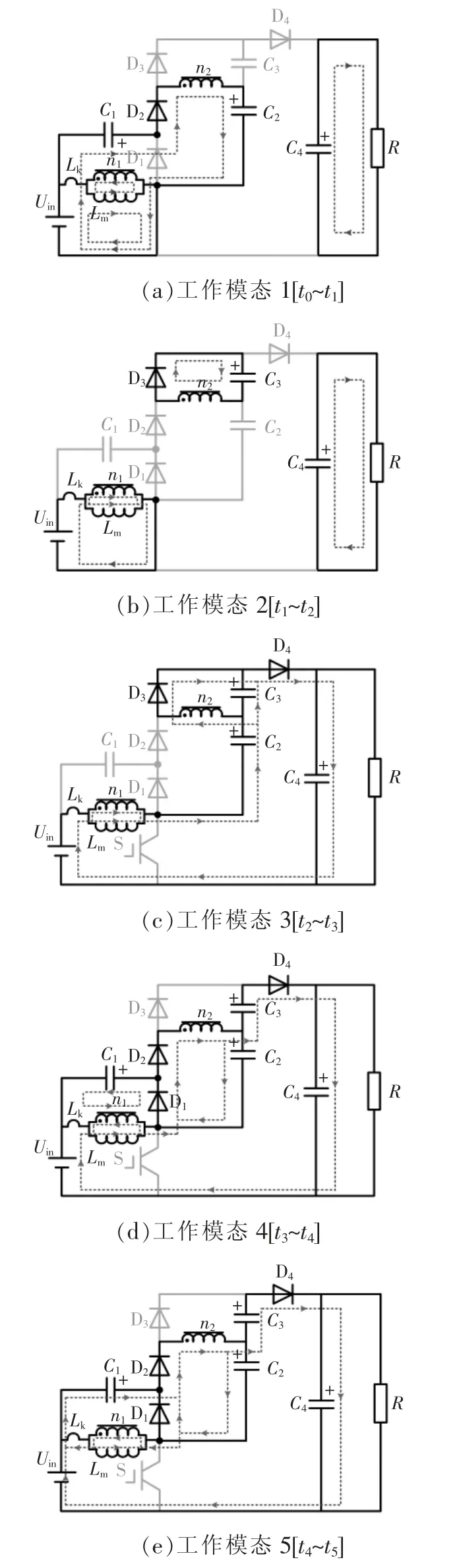
图2 各工作模态等效电路原理Fig.2 Schematic of equivalent circuit in each operation mode

图3 变换器稳态工作时的主要波形Fig.3 Main operation waveforms of converter in steady state

（1）工作模态1：t0～t1。如图2（a）所示，此模态下存在3 个能量传输回路。回路1：输入电源Uin-电容C1-线圈n2-电容C2-输入电源Uin，电容C2储能。回路2：输入电源Uin-漏感Lk-励磁电感Lm-输入电源Uin，漏感与励磁电感储能。电路3：电容C4给电阻R 供电。

此模态下耦合电感副边线圈放磁，副边电流in2逐渐减小到0（规定流入同名端为电流的正方向），二极管D2关断后进入下一个模态。此时，Lm和Lk的电流iLm和iLk分别为

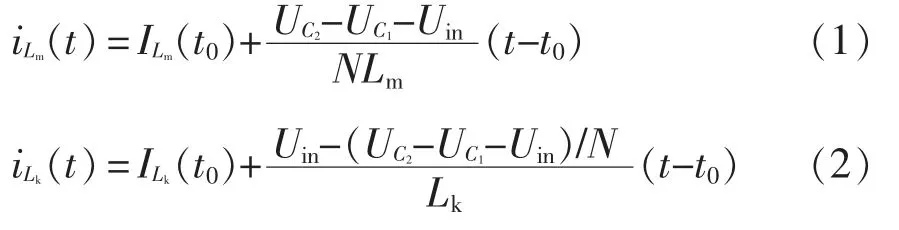
式中：ILm（t0）、ILk（t0）分别为Lm和Lk电流的起始值；Uin为输入电压；UC1、UC2分别为电容C1、C2的电压。

（2）工作模态2：t1～t2。如图2（b）所示，此模态下存在3 个能量传输回路。回路1：输入电源Uin-漏感Lk-励磁电感Lm-输入电源Uin，漏感与励磁电感储能。回路2：线圈n2-电容C3-线圈n2，电容C3储能。回路3：电容C4-电阻R-电容C4，电容C4给电阻R供电。

原边线圈此时在输入电压作用下继续充磁，电流iLm和iLk线性增加，耦合电感副边线圈电流in2从0开始反向线性增加，此阶段副边线圈充磁。此时，电流iLm和iLk分别为

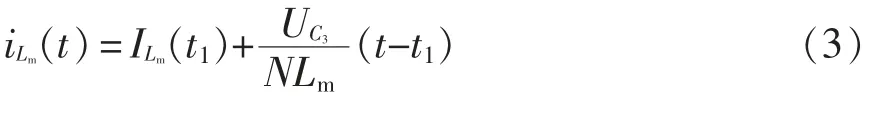
式中：ILm（t1）和ILk（t1）分别为t1时刻Lm和Lk的电流；UC3为电容C3的电压。

（3）工作模态3：t2～t3。如图2（c）所示，此模态下存在2 个能量传输回路。回路1：输入电源Uin-漏感Lk-励磁电感Lm-电容C2-线圈n2-电容C4（电阻R）-输入电源Uin，电容C4充电。回路2：输入电源Uin-漏感Lk-励磁电感Lm-电容C2-电容C3-电容C4（电阻R）-输入电源Uin，电容C4充电。

耦合电感副边线圈放磁，副边电流in2反向逐渐减小到0。漏感与励磁电感开始放磁，电流iLm和iLk线性减小。此时，电流iLm和iLk分别为

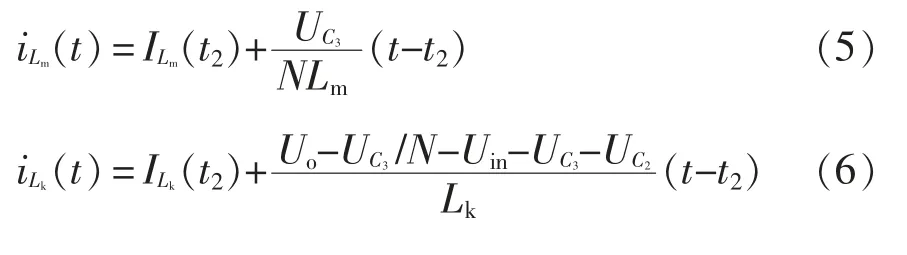
式中：ILm（t2）和ILk（t2）分别为t2时刻Lm和Lk的电流；Uo为输出电压。

（4）工作模态4：t3～t4。如图2（d）所示，此模态下存在3 个能量传输回路。回路1：输入电源Uin-漏感Lk-励磁电感Lm-线圈n2-电容C3-电容C4（电阻R）-输入电源Uin，电容C4充电。回路2：线圈n2-电容C2-线圈n2，电容C2充电。回路3：漏感Lk-励磁电感Lm-电容C1-漏感Lk，电容C1充电。

漏感Lk的部分能量经二极管D1给电容C1充电，有效地吸收了漏电感能量，漏感电流线性减小至0，耦合电感副边线圈充磁，in2从0 开始线性增加。此时，电流iLm和iLk分别为

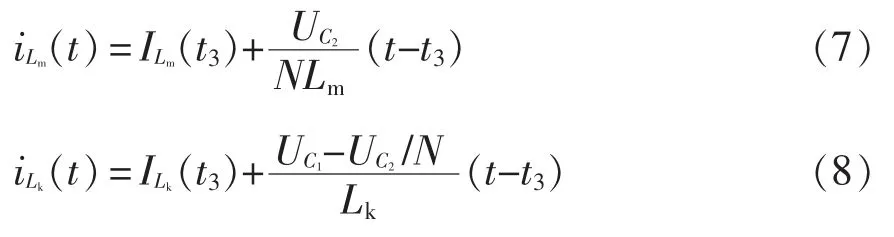
式中：ILm（t3）和ILk（t3）分别为t3时刻Lm和Lk的电流；Uo为输出电压。

（5）工作模态5：t4～t5。如图2（e）所示，此模态下存在3 个能量传输回路。回路1：输入电源Uin-电容C1-线圈n2-电容C3-电容C4（电阻R）-输入电源Uin，电容C4充电。回路2：线圈n2-电容C2-线圈n2，电容C2充电。回路3：漏感Lk-电容C1-线圈n2-电容C2-线圈n1-漏感Lk，漏感Lk反向充磁。

在t4时刻，耦合电感原边电流大于励磁电感电流，漏感电流方向改变，从0 开始反向线性增加，励磁电感电流依旧保持线性减小，耦合电感副边电流线性增加继续充磁，电容C1处于放电状态。此时，电流iLm和iLk同工作模态4 中的式（7）和式（8）。

2 变换器稳态性能分析

2.1 电压增益分析

由工作模态1 和2 可得电感Lm的电压为

由工作模态2 可得

由工作模态4 可得

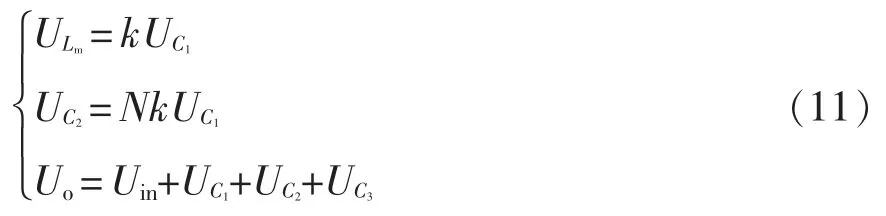
由Lm伏秒平衡可得

式中，D 为占空比。

由式（10）和式（12）解得的UC3、UC1代入式（11），可得电压增益M 为

当k=1 时,电压增益为

分析式（14）可知，电压增益M 作为因变量会随着2 个自变量占空比D、匝数比N 的变化而变化。当N=2、3、4 时，M 随D 变化而变化的关系如图4 所示。需要注意的是图4 中当占空比D=0 时，开关管不工作，耦合电感失效，所以匝数比N=0，此时，变换器电压增益M=1。

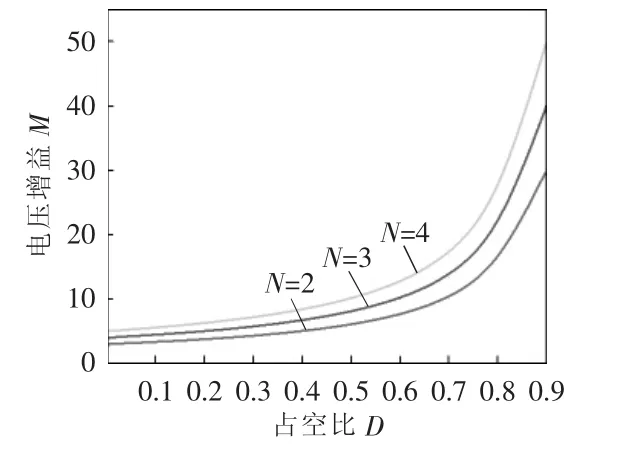
图4 N=2、3、4 时，电压增益M 与占空比D 的关系Fig.4 Relationship between voltage gain M and duty cycle D when N equals 2,3 and 4

由图4 可得，当电压增益M 固定，随着匝数比的增大，所需要的占空比会减小，因此，可以通过设置更大的匝数比来提升电压，同时还能选择更合理的占空比，提升了变换器的整体性能。

分析式（13）可知，电压增益M 受到了3 个自变量（k、N、D）的约束，且漏感Lk对变换器的占空比D存在影响[14]。图5 给出了D=0.5 时M 与N 和k 的三维关系曲线。由图5 可得，当匝数比N 相同时，电压增益M 与耦合系数k 正相关。因此，在实际应用中通过合理设计来确保k 尽可能为1。

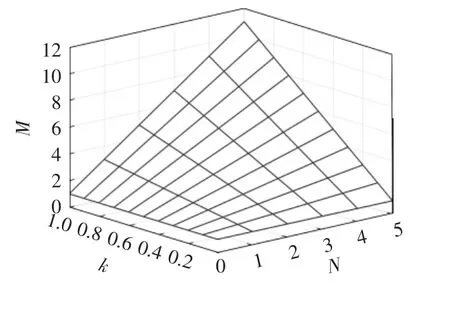
图5 D=0.5 时，M 与N 和k 的关系Fig.5 Relationship among M,N and k when D=0.5

2.2 电压应力分析

由工作模态1 可列出D1、D3的电压应力为

式中：UD1，stress、UD3，stress分别为D1、D3的电压应力；Un2为副边线圈n2的电压。

由工作模态2 可列出D2、D4的电压应力为

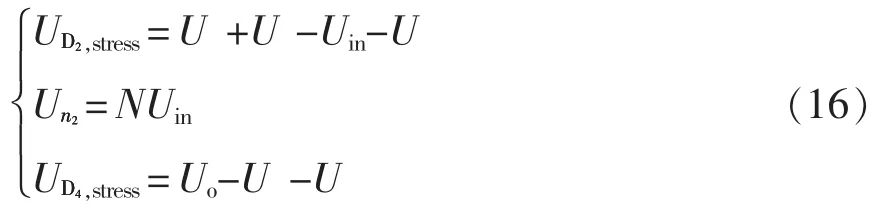
式中，UD2，stress、UD4，stress分别为D2、D4的电压应力。

由工作模态3 可列出开关管S 的电压应力为

式中，USD，stress为开关管S 的电压应力。

令耦合系数k=1，将式（10）—式（13）代入式（15）—式（17）可得各功率器件的电压应力分别为

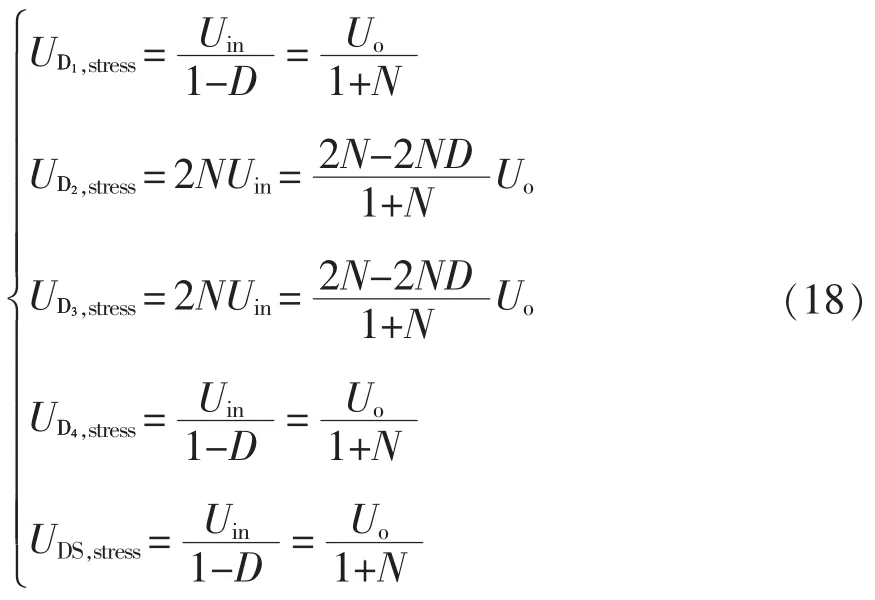
分析式（18）可知，所有功率器件的电压应力都低于输出电压，选择低耐压（寄生参数小）的器件会更节约成本，经济效益更高，所以这也为器件的选型提供了一定的参考。

2.3 电感的设计

若不考虑电路中间造成的损耗值，那么，遵循能量守恒定律，则输入功率完全给到输出，即

式中：Iin为输入电流平均值；Io为输出电流平均值。

当耦合系数k=1 时，有Iin=ILm，根据功率转换关系可得励磁电感电流平均值IˉLm和励磁电感电流纹波ΔILm为

式中，f 为开关频率。

根据式（20）可得励磁电感最小电流ILm.min为

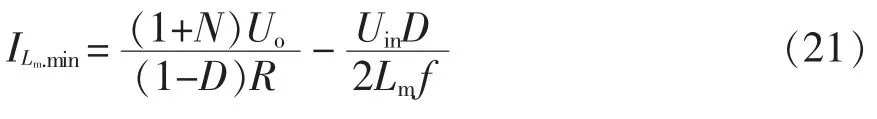
令ILm.min=0，可得临界励磁电感LmC为

为确保变换器能在连续导电模式下稳定工作，那么需要满足的条件为ILm.min≥0，因此，在对励磁电感进行选取时，需要满足Lm≥LmC。

2.4 电容的设计

变换器须满足输出纹波电压ΔUo要求[15]，滤波电容起到了关键性的作用。在一个周期内，开关管S 导通，滤波电容单独为电阻R 供电，此时负载电阻两端的电压就是由滤波电容C 所决定的，根据电路定律可以得到输出纹波电压ΔUo为

通过分析式（23）可得，输出纹波电压与滤波电容存在反比关系，可以得到滤波电容为

当按照所规定的参数设计时，通过式（24）可以计算出电容，因此，在变换器设计选取电容时应该选取比其计算值更大的电容。

2.5 耦合电感匝数比的设计

由于耦合电感的匝数比对变换器的电压增益以及功率器件的电压应力有着重要的影响，因此对耦合电感匝数比的设计就有很大的必要性。根据式（14）可得关于耦合电感匝数比为

根据式（25）可知，在电路设计时，确定好输入和输出电压，选取合理的占空比，可以计算出匝数比，再根据计算值代入功率器件应力表达式来最终确定一个较为合理的匝数比。

3 变换器的性能对比

不同变换器性能对比如表2 所示。由表2 可知：占空比相同且匝数比N≥1 时，电压增益由上而下越来越大，本文所提变换器的电压增益最大；开关管与输出二极管的电压应力由上而下越来越小，本文所提变换器的最小，充分说明了所提变换器的性能更优，其应用范围会更加广泛。

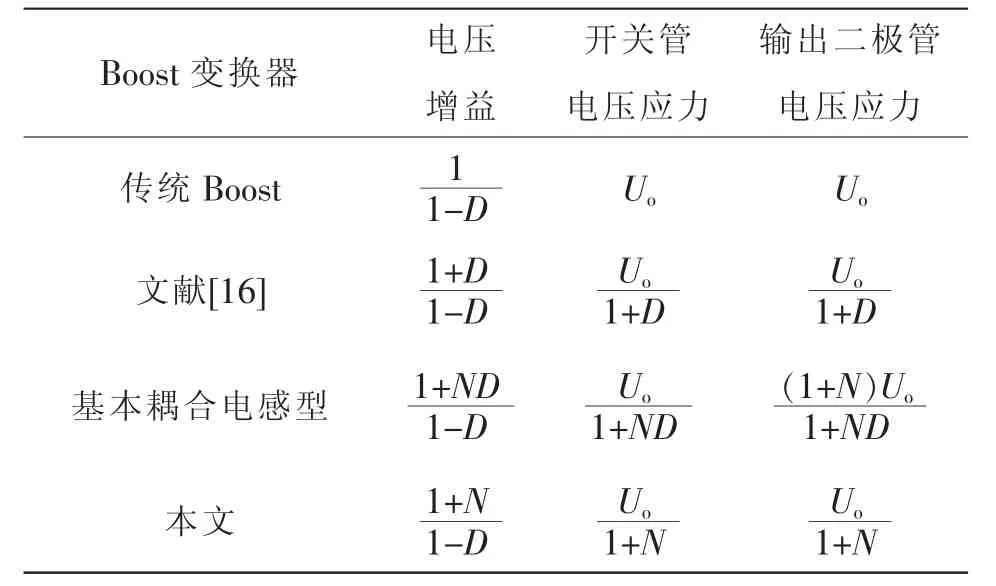
表2 不同变换器性能对比Tab.2 Comparison of performance among different converters

当取耦合系数k=1、匝数比N=2 时，各高增益变换器增益对比如图6 所示。图6 中，当占空比D=0 时，开关管不工作，本文所提变换器中耦合电感失效，N=0，此时变换器电压增益M=1。由图6 可见，所有变换器电压增益都随着占空比的变化而变化，且变化趋势属于正相关的关系；当占空比固定时，所提变换器拥有更高的电压增益，在此基础上，所提变换器还多了一个限制电压增益的变量（匝数比），从而在实际运用中通过合理地设计匝数比，可以选择更合适的占空比来达到高增益的目的。

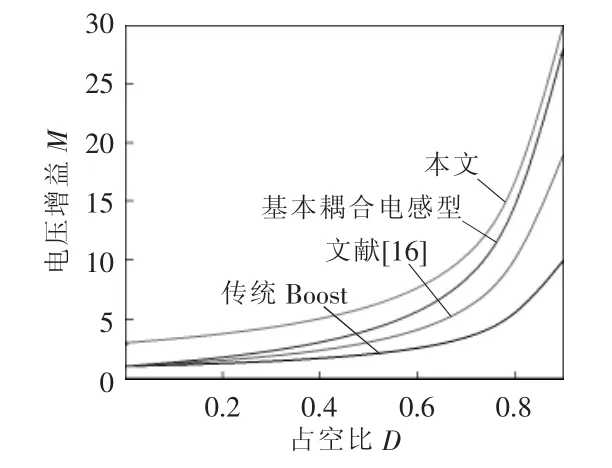
图6 各高增益变换器增益对比Fig.6 Comparison of gain among different high-gain converters

4 实验验证

通过实验平台制作了一台100 W 的模型进行验证，实验参数见表3。

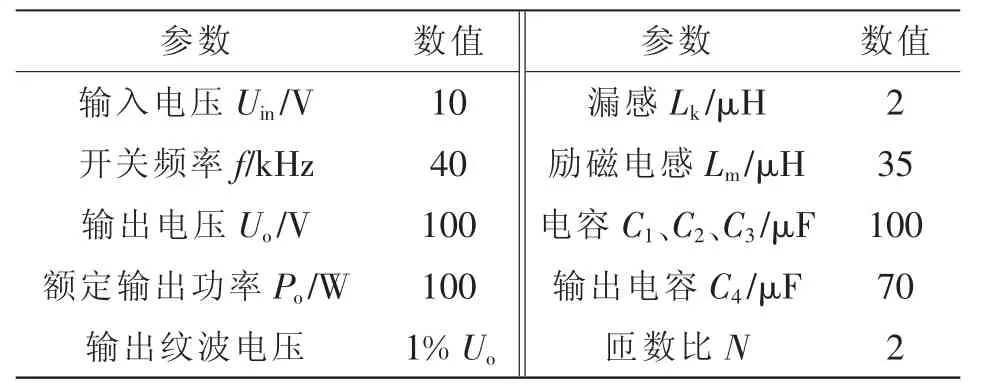
表3 实验电路参数Tab.3 Parameters of experimental circuit

根据式（22）可计算出耦合电感Lm为8.75 μH，由于实验误差和非理想化应取4 倍裕量Lm=35 μH。根据式（24）可计算出输出滤波电容为17.5 μF，同样取4 倍裕量取为70 μF。实验波形如图7 所示，通过实验可得变换器的效率曲线如图8 所示。

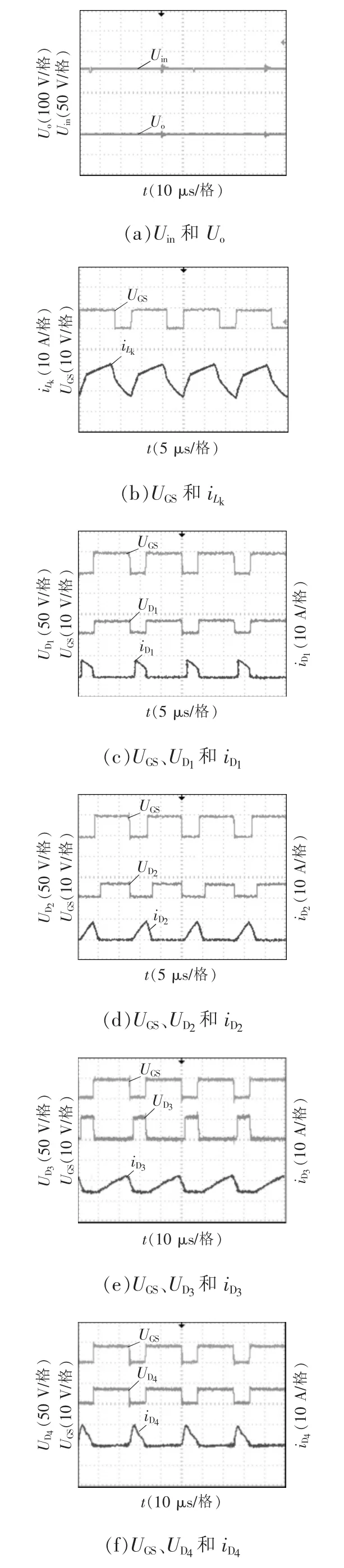
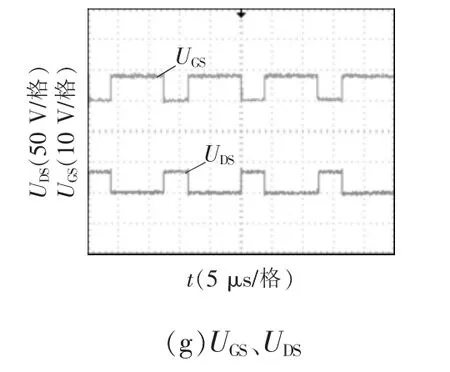
图7 实验波形Fig.7 Experimental waveforms

图8 变换器效率曲线Fig.8 Efficiency curve of converter

通过图7（a）输入（输出）的电压波形，可以看到，成功地实现了电压的高增益。通过图7（b）原边漏感的电流波形可以看到，电流呈现周期性的双向流动，这是由副边线圈所决定的。通过图7（c）—（f）各二极管电流及承受电压波形可以看到，各二极管电压应力与理论计算值一致，且小于输出电压，双倍压单元的组合优势得到了体现，二极管D2和D3实现了零电流关断，二极管D4关断时电流很小，减小了二极管的工作损耗，达到了提升变换器性能的目的。通过图7（g）功率开关管两端电压波形，开关管关断时没有电压尖峰，说明漏感能量被吸收。通过分析实验结果，一方面，电压高增益的成功实现，另一方面，变换器的性能得到优化，变换器的理论分析得到了充分的验证。

5 结论

（1）只用一个开关管控制，控制简单且可靠性高。

（2）通过双倍压单元的组合和耦合电感的加入，可以设计匝数比来合理选择占空比。

（3）所有功率器件电压应力均小于输出电压，可选低耐压（寄生参数小）的功率器件。

（4）解决了电路谐振问题，电压尖峰得到了改善，提高了效率。

（5）缓解了二极管反向恢复问题，提高了性能。