采用VSG 策略的MMC 阻抗建模及并网稳定性分析

孙 杰，尹太元，王 跃，刘 普，王晓雷，乐 波

（1.西安交通大学电气工程学院，西安 710049；2.郑州轻工业大学电气与信息工程学院，郑州 450000；3.中原工学院电子信息学院，郑州 450007；4.国网经济技术研究院有限公司，北京 102209）

模块化多电平换流器MMC（modular multi-level converter）由于其模块化、开关频率低、输出电压波形畸变小等优点，逐渐成为柔性直流输电系统中广泛采用的换流器[1-3]。近年来，分布式能源大规模并网，电网的惯性和调节能力随着分布式能源的高渗透率而降低[4]，虚拟同步发电机VSG（virtual syn-chronous generator）控制技术由于具有类似同步发电机的调频和调压能力，并能够为系统提供一定的惯性和阻尼支撑等优点，为解决新能源大规模并网所带来的稳定性问题提供了新的解决方案，逐渐得到国内外学者的高度重视和广泛研究[5-6]。

基于端口阻抗的稳定性分析法是目前被学术界和工业界广泛采用的稳定性分析方法，多个柔直工程均采用了此方法，并且其准确性和有效性也得到了充分的验证[7-9]。目前采用VSG 控制策略的并网逆变器的阻抗建模多集中在两电平换流器，文献[10-11]研究了电压型VSG 和电流型VSG 的小信号阻抗建模及其与弱电网的交互稳定性。而MMC 由于内部动态特性复杂，在子模块电容电压和桥臂电流中含有很多谐波，且不同谐波之间存在复杂的耦合关系[12-15]，相较于VSC 的阻抗建模要复杂得多，且其阻抗模型跟VSC 有较大差别。文献[16]首次基于谐波线性化的建模方法建立了包含环流抑制和锁相环的单电流环MMC 整流器的阻抗模型。文献[17]基于谐波状态空间法建立了MMC 交流侧阻抗，分析了级联系统的稳定性。文献[18]对具有完整控制环路的MMC-HVDC 系统进行了序阻抗建模并进行了稳定性分析。

但是上述文献均未涉及VSG 控制策略下的MMC 阻抗建模，其端口阻抗特性尚不明确，也鲜有基于阻抗分析法对采用VSG 控制策略的MMC 进行并网稳定性研究，而由于VSG 控制策略的MMC在接入弱电网时对电网具有惯性和阻尼支撑的优点，未来在柔直领域中有广阔的应用前景，因而十分有必要建立其阻抗模型，并研究其与弱电网交互时的稳定性问题，这对基于MMC 拓扑在不同控制模式下的阻抗模型和在柔直工程中的稳定性研究是一项重要补充，能够为其并网安全运行提供理论依据，并对其参数设计提供理论指导。

本文首先研究MMC 的VSG 控制策略，然后基于谐波线性化方法详细推导VSG 控制策略下的MMC 阻抗模型，并进行验证。然后根据得到的MMC 阻抗伯德图，分析其阻抗特性，研究VSG 控制参数对MMC 阻抗特性的影响以及VSG 控制策略下MMC 的阻抗灵敏度。再结合电网阻抗特性，并根据奈奎斯特稳定判据分析在弱电网条件下VSG控制策略下MMC 的并网稳定性。最后通过实验验证上述稳定性分析的正确性，本文研究结果可为采用VSG 控制策略的MMC 并网系统的控制和稳定性分析以及稳定性优化提供参考。

1 MMC 拓扑及其VSG 控制策略

MMC 的结构框图如图1 所示。其由6 个三相桥臂组成，每相上下2 个桥臂完全相同，每个桥臂由N 个半桥子模块和1 个桥臂电感L 组成，L 的等效寄生电感为rL。图1 中，vj（j=a，b，c）为MMC 交流端口电压，ij（j=a，b，c）为MMC 交流端口电流，iju（j=a，b，c）为流过三相上桥臂的电流，ijl（j=a，b，c）为流过三相下桥臂的电流，Udc为MMC 直流侧电压。通过控制桥臂子模块投入的数量改变交流端口电压，桥臂电感L 可以抑制相间环流并减少内部电流的谐波含量。

图1 MMC 的结构框图Fig.1 Structural diagram of MMC

图2 为包含环流抑制环节的VSG 控制框图，包括功率计算部分、功率控制部分和环流抑制部分。功率计算部分及功率控制部分主要是为了模拟同步发电机的特性，其又分为有功-频率控制和无功-电压控制。有功-频率控制主要是为了模拟同步发电机的一次调频特性和转子惯性；无功-电压控制是为了模拟电压调节特性。

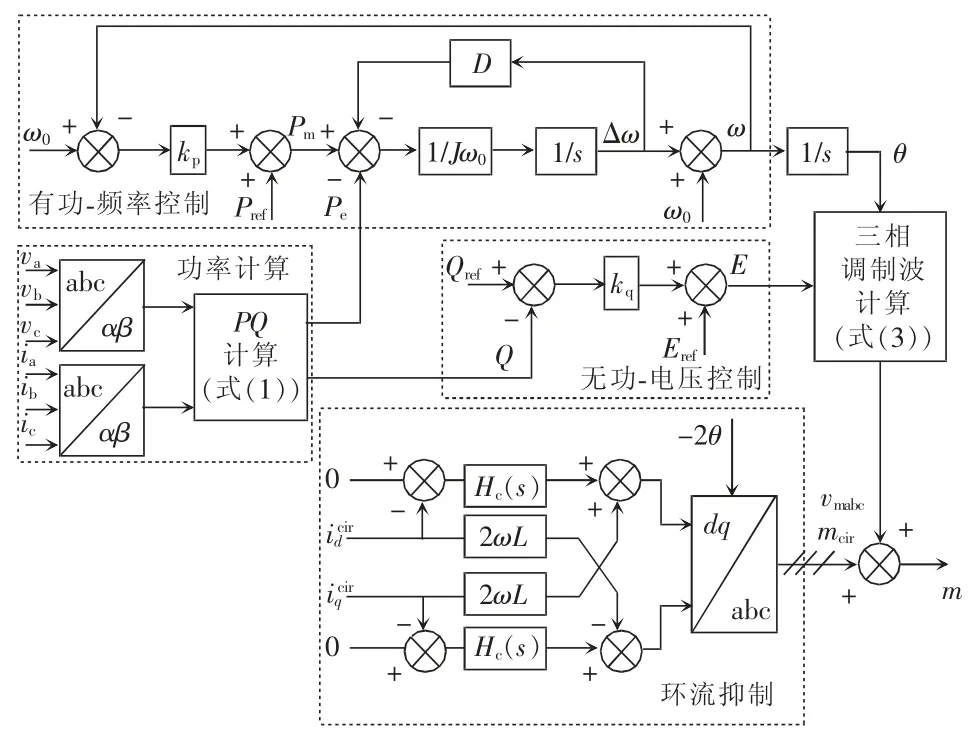
图2 VSG 控制框图Fig.2 Block diagram of VSG control

VSG 输出有功功率Pe和输出无功功率Q 由瞬时功率理论计算，其计算公式为

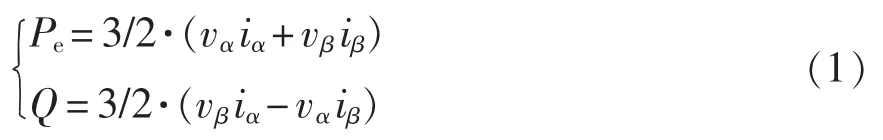
式中：vα、vβ为由三相输出电压经Clark 变换得到的输出电压；iα、iβ为由三相输出电流经Clark 变换得到的输出电流。

VSG 有功控制器的数学方程为

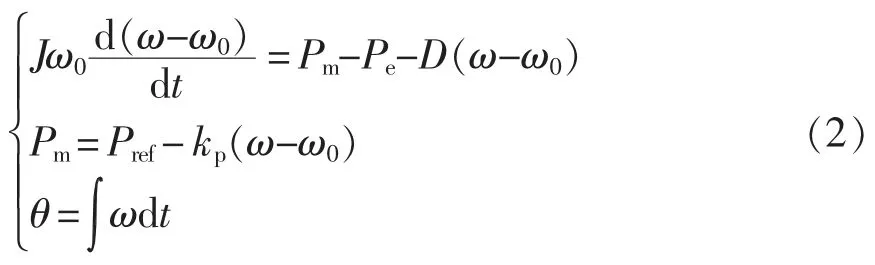
式中：J 为虚拟转动惯量；ω0为电网的额定角频率；ω 为VSG 有功控制环路的输出角频率；Pm为虚拟机械功率；Pe为电磁功率；D 为阻尼系数；Pref为有功功率指令；kp为有功-频率下垂系数；θ 为VSG 输出角度。

VSG 无功控制器的数学方程为

式中：E 为虚拟内电势的峰值；Eref为内电势峰值指令；Qref为无功功率指令；Q 为输出无功功率；kq为无功-电压下垂系数。

VSG 的有功-频率控制器和无功-电压控制器的输出共同决定其产生的调制波，数学方程为

式中，vma、vmb、vmc为VSG 生成的调制波。

环流抑制控制器生成的调制波为mcir，将其与vmabc叠加，即可得到MMC 的调制波信号m。

2 VSG 控制策略的MMC 阻抗建模

谐波线性化是一种获取换流器阻抗的简便方法，其应用范围比较广。相比于传统dq 坐标系中的建模，谐波线性化的稳态运行轨迹可以包含任意数量的谐波，计算出来的阻抗有清晰的物理解释并可以直接测量[19]。下面基于谐波线性化思想对基于VSG控制策略下的MMC 进行阻抗建模。

2.1 MMC 电气系统小信号模型

基于谐波线性化的阻抗建模首先需要在MMC交流侧注入频率为fp的扰动电压，以a 相为例，加入扰动电压之后的a 相端口电压va（t）为

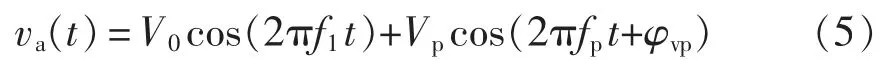
式中：V0为a 相电网电压的幅值；f1为a 相电网电压的频率；Vp为在MMC 交流端口注入的扰动电压幅值；φvp为其初相位，对于b 相和c 相，只须根据注入扰动信号的正负序将相位在a 相相位的基础上超前或滞后2π/3 即可。

MMC 由于子模块数目很多，等效开关频率极高，可以认为所有子模块电容电压始终保持均衡[20]，根据MMC 的对称性，以a 相上桥臂为例，可以得到MMC 的功率级小信号模型[16]为

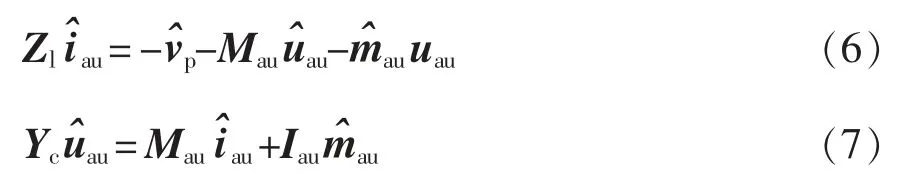
对于给定频率为fp的电压扰动将会导致系统产生一系列频率为fp±kf1（k=1，2，…，n）的小信号谐波分量，虽然理论上会产生无限多频次的谐波，但这些谐波的幅值会随着k 的增加而减小[21-22]，考虑数学运算的复杂性和阻抗建模精度的要求，通常只须考虑3 次以内的谐波即可,表1 给出了各频次谐波正负序和差模共模的信息[16]。

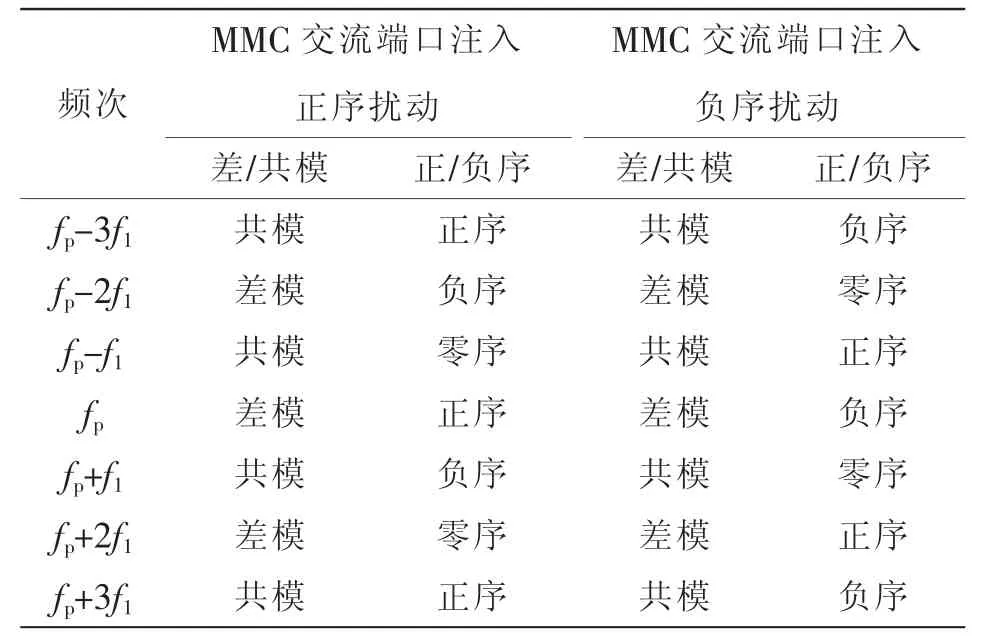
表1 小信号谐波之间的关系Tab.1 Relationship among small-signal harmonics

2.2 MMC 控制部分的小信号模型

根据式（6）和式（7）可以看出，Iau、uau和Mau是稳态量，可以从MMC 输出功率计算得到，可以消掉，此时如果能用和表示，那么就可以通过计算和的比值进而得到MMC 的阻抗。下面对MMC 交流端口注入正序小扰动电压时的阻抗进行详细推导，MMC 交流端口注入负序电压扰动时的推导过程与正序时类似，本文不再赘述。

在MMC 交流端口注入fp频次的扰动电压，所产生的小信号电流响应中只有差模量会流到交流端口，根据表1 中的正负序和差模共模关系，对于正序电压扰动而言，其产生的差模量的频次分别为fp和fp-2f1频次，分别为差模正序信号和差模负序信号，其三相表达式为

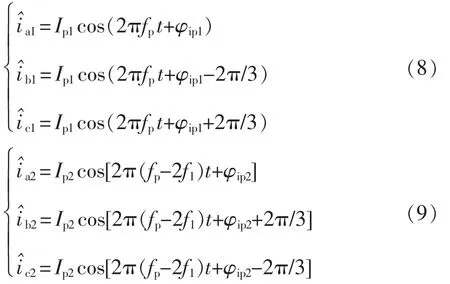
对式（8）和式（9）进行Clark 变换，将小扰动电压和2 个频次的小信号电流转换到αβ 坐标系下，Clark变换矩阵Tαβ和变换后小信号电压、电流分别为

设V0和I0为稳态电压和电流的幅值，Vα和Vβ为αβ 坐标系下MMC 的稳态电压，Iα和Iβ为αβ 坐标系下MMC 的稳态电流，表达式分别为

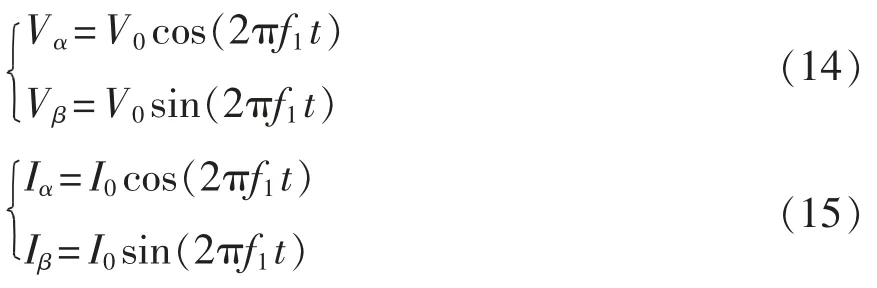
对于VSG 功率控制环路，无功控制环的输出电压可视为定值[23]，根据式（1）可以得到小信号形式的有功功率为

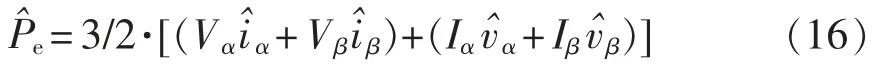
由式（16）可以看出，小信号有功功率中包含小信号电压和2 个频次小信号电流的影响，因此小信号有功功率可以分为3 部分，其中，对于fp频次电流部分为

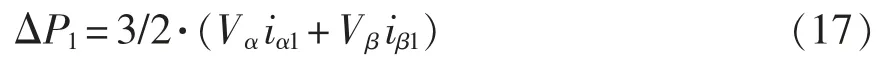
对于fp-2f1频次电流部分为

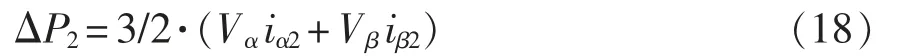
对于fp频次电压部分为

由图2 所示的VSG 控制框图可得VSG 控制部分的传递函数M（s）为

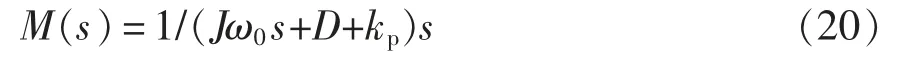
M（s）代表了从电磁功率Pe经有功-频率控制环节得到频率后，再积分成角度θ 的传递函数。

燃气企业因为受到自身特性的影响，在开展财务信息化建设工作时，根据需要可以将不同地点、区域具有共性较强的、重复率高的、易于标准化和流程化的财务业务或职能从分、子公司中剥离出来，之后将其融合到信息平台中，实现信息传递和共享。只有这样，才能将规模效应以及协同效应充分发挥，减少财务运行成本，提升财务运营效率以及服务质量，从而降低财务运行风险，给燃气企业的健康发展营造良好的条件。

VSG 控制环路输出的小信号相角为

此时在VSG 输出的三相调制波相角中引入了相角扰动Δθ。假设没有扰动时的相角为θ0，则有

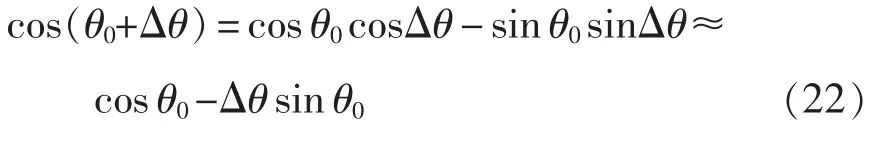
将式（21）、式（22）代入式（4）中并忽略大信号项，可以得到VSG 控制环路生成的小信号调制波为

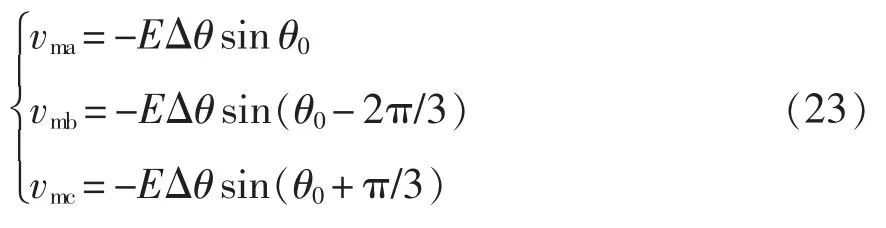
综上并利用三角函数积化和差化简，由fp频次电流所影响产生的a 相小信号调制波为

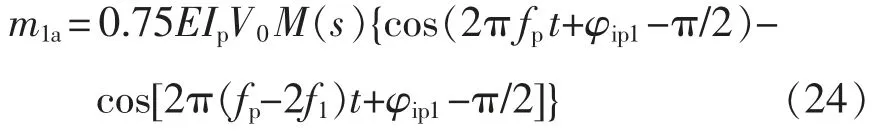
结合式（8）和式（24）可以看出，fp频次的小信号电流在调制波中产生fp和fp-2f1两个频次的谐波，且与原来的小信号电流相比均有π/2 的相位延迟。因此，fp频次的小信号电流对VSG 控制环路生成调制波的系数矩阵表示为

同理，fp-2f1频次的小信号电流对VSG 控制环路生成调制波的系数矩阵表示为

其中

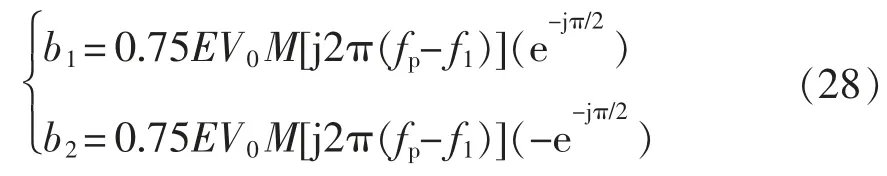
因此，VSG 控制环路中小信号电流对调制波的系数矩阵表示为

fp频次的小信号电压对VSG 控制回路生成调制波的系数矩阵表示为

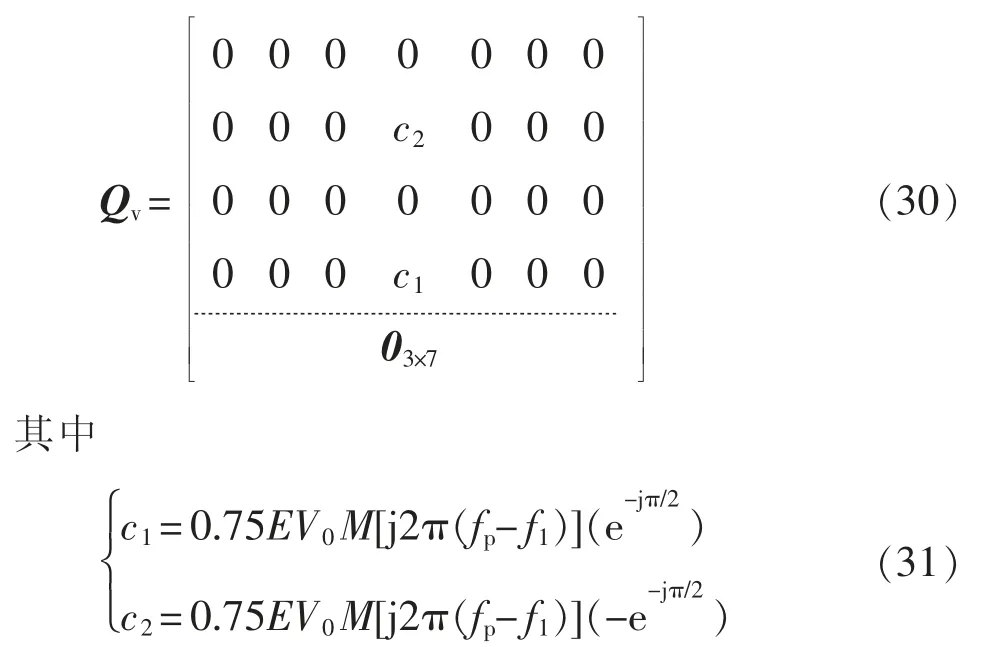
环流抑制环对调制波的系数矩阵可以表示为[10]

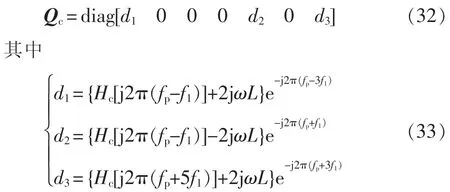
式中，Hc为环流抑制环的传递函数。

2.3 MMC 阻抗模型的仿真验证

各控制环路调制波的影响可以表示为

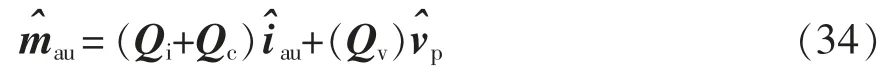
将式（34）代入式（6）和式（7），可得到小扰动电压与桥臂小信号电流的关系为

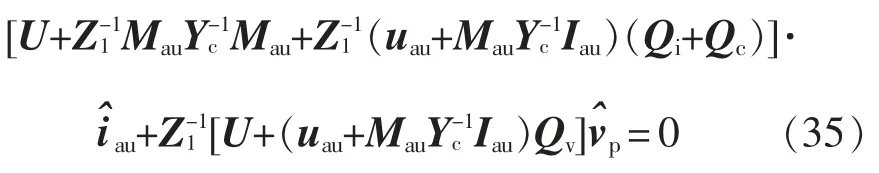
式中，U 为7 阶单位矩阵。

由此可得小扰动电压与桥臂小信号电流的7阶导纳矩阵为

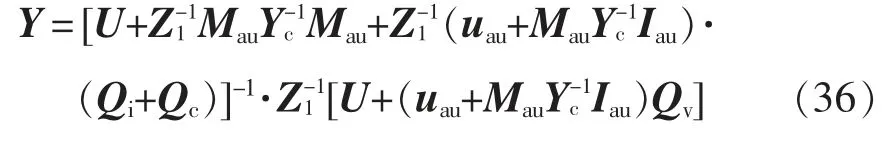
由于fp频次的相电流是桥臂电流的2 倍[16]，因此MMC 在fp频次的阻抗模型为

为了验证上述建立阻抗模型的正确性，在Matlab/Simulink 中搭建仿真模型，模型参数如表2所示，通过频率扫描法获取仿真阻抗幅频特性和相频特性并与阻抗模型的解析值进行对比验证。

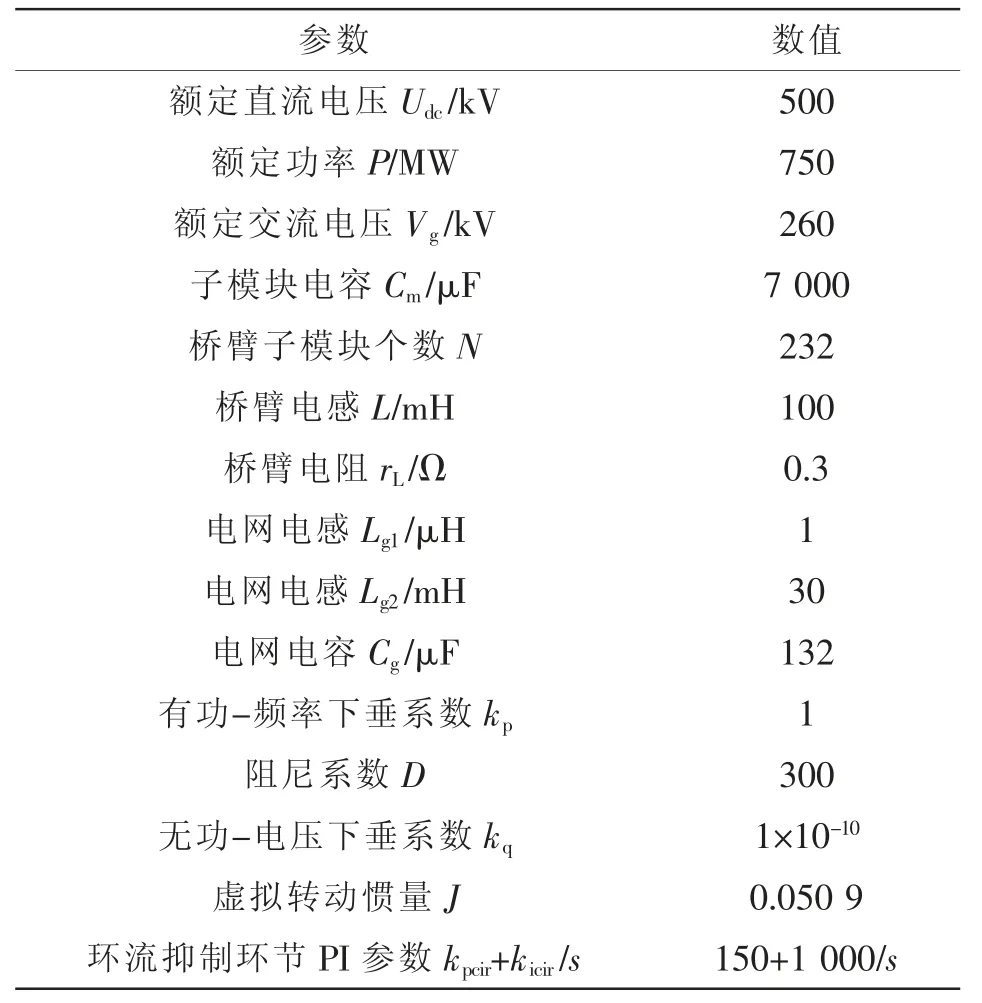
表2 MMC 的系统和控制参数Tab.2 System and control parameters of MMC

MMC 阻抗模型扫频值与解析值对比结果如图3 所示。由图3 可见，解析值与扫频值吻合，验证了上述所建立阻抗模型的正确性。

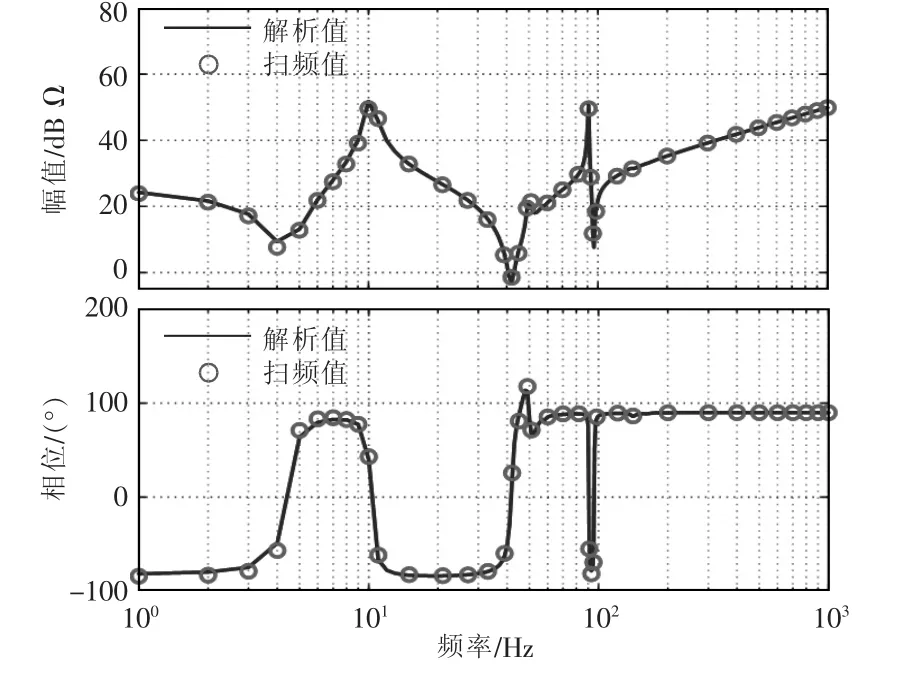
图3 MMC 阻抗扫频值与解析值对比结果Fig.3 Results of comparison between frequency scanning and analytical values of MMC impedance

3 MMC 并网稳定性分析

3.1 VSG 控制参数对MMC 阻抗的影响

3.1.1 控制参数对阻抗曲线的影响

有功-频率下垂系数kp对MMC 阻抗的影响如图4 所示，对比3 组参数（kp=1，10，100）得到的阻抗曲线，kp增大会使50 Hz 附近的2 个阻抗尖峰变小，而其他频段的阻抗特性几乎没有变化，说明kp的改变对其他频段的阻抗特性影响不大。

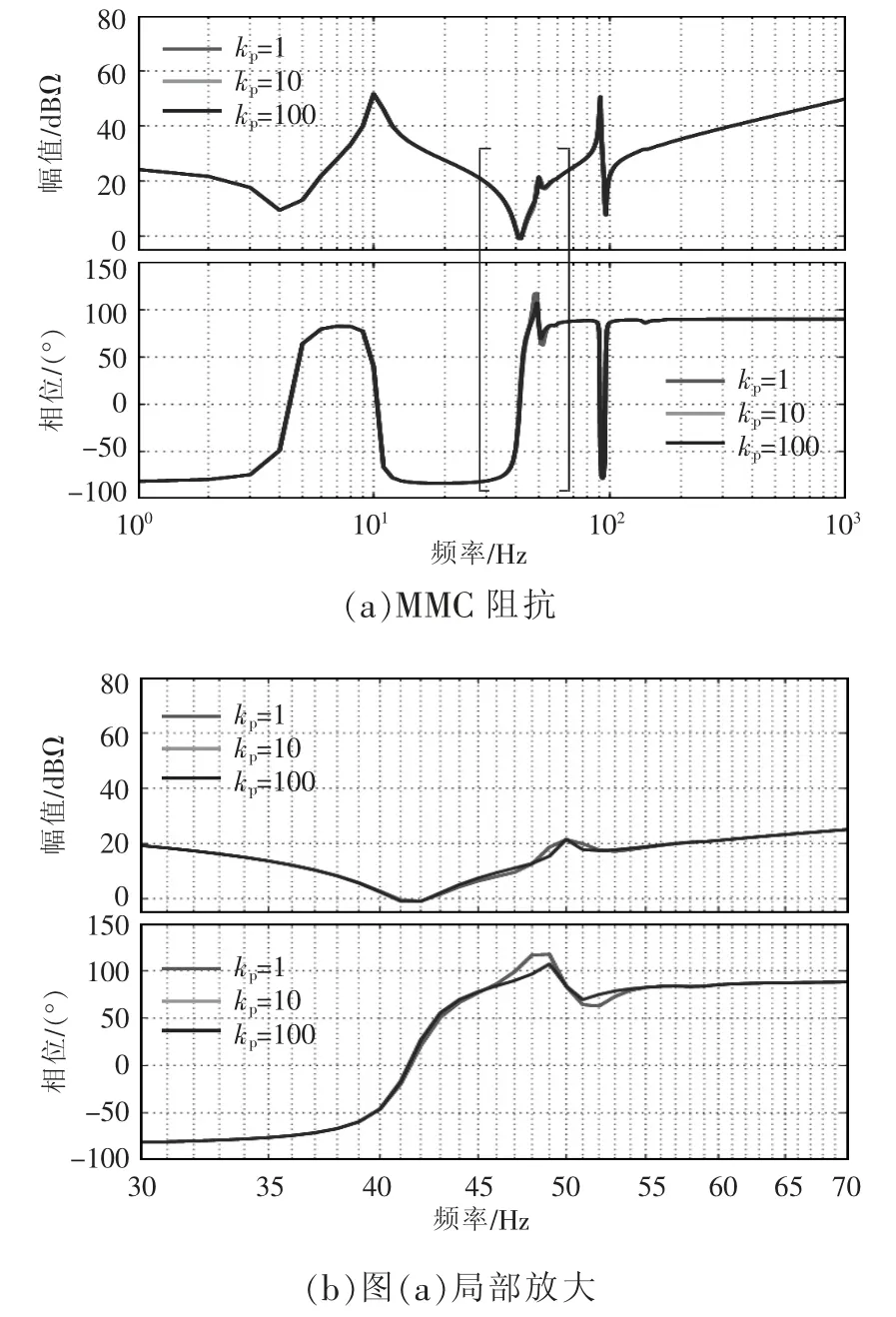
图4 kp=1、10、100 时的MMC 阻抗Fig.4 Impedance of MMC when kp equals 1,10 and 100,respectively

阻尼系数D 对MMC 阻抗的影响如图5 所示，从3 组不同的参数（D=200，300，400）得到的阻抗曲线可以看出，阻尼系数对MMC 阻抗的影响主要在45～55 Hz，阻尼系数越大，50 Hz 附近的2 个尖峰越小，系统阻尼越强。而其他频段的阻抗特性几乎没有变化，说明D 的改变对其他频段的阻抗特性影响不大。

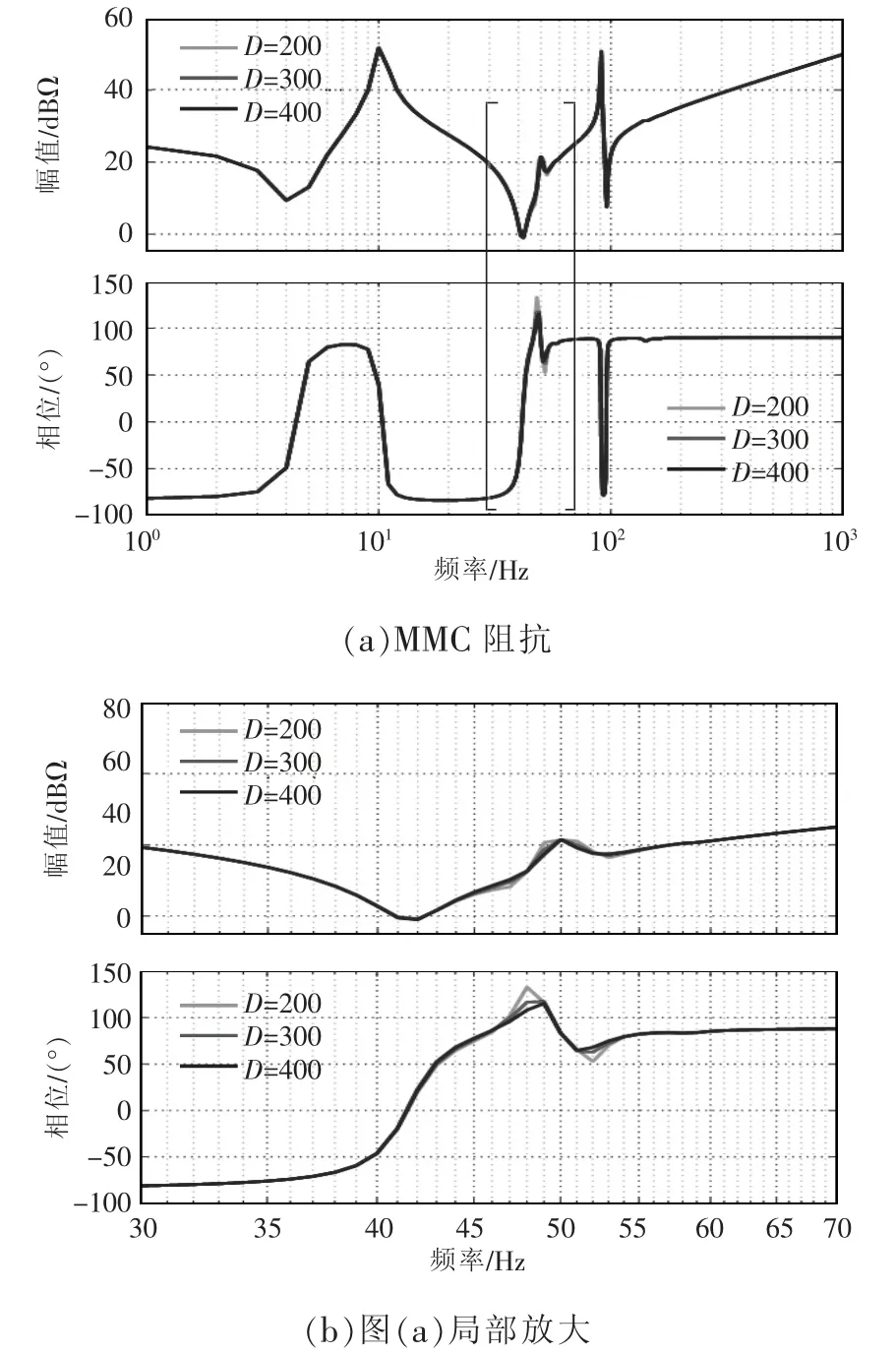
图5 D=200、300、400 时的MMC 阻抗Fig.5 Impedance of MMC when D equals 200,300 and 400,respectively

虚拟转动惯量J 对MMC 阻抗的影响如图6 所示，从3 组不同的参数（J=0.025 4,0.050 9,0.102 0）得到的阻抗曲线可以看出，虚拟转动惯量对MMC阻抗的影响主要在40～55 Hz。而其他频段的阻抗特性几乎没有变化，说明J 的改变对其他频段的阻抗特性影响不大。

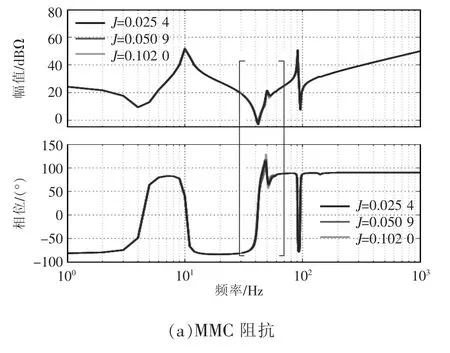
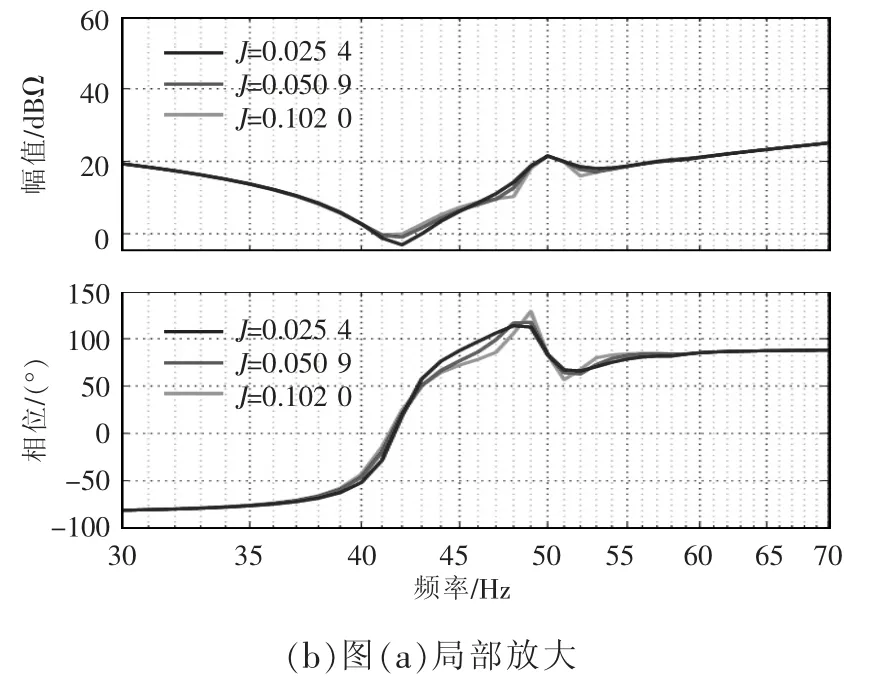
图6 J=0.025 4、0.050 9、0.102 0 时的MMC 阻抗Fig.6 Impedance of MMC when J equals 0.025 4,0.050 9 and 0.102 0,respectively

3.1.2 控制参数的阻抗灵敏度分析

控制参数的阻抗灵敏度能够反映当控制器不同控制参数变化时对换流器端口阻抗特性的影响大小，当一个控制参数在某个频段得到的灵敏度值越大，说明该控制参数在该频段对换流器阻抗特性的影响越大，也即阻抗特性在此频段对该参数的变化越敏感；反之，当一个控制参数在某个频段得到的灵敏度值越小时，说明该控制参数在该频段对换流器阻抗特性的影响越小，也即阻抗特性在此频段对该参数的变化越不敏感。控制参数的阻抗灵敏度包括阻抗幅值灵敏度和阻抗相角灵敏度，定义为

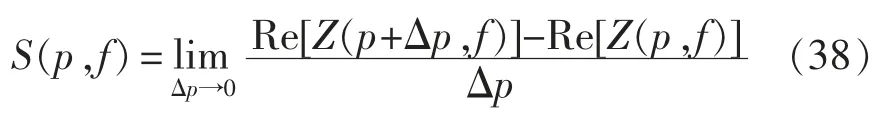
式中：p 为原本控制参数；Δp 为控制参数变化量；S为控制参数阻抗灵敏度。

有功-频率下垂系数kp的阻抗灵敏度如图7 所示，可见，在频率为47、49、51 Hz 时幅值灵敏度曲线较高，说明在这3 个频率附近的阻抗幅值对kp的变化比较敏感，而1～36 Hz、60～1 000 Hz 频段的阻抗幅值灵敏度曲线几乎与横轴重合，说明在这些频段kp的变化不会使阻抗幅值产生明显变化；在频率为42、48、52 Hz 时相角灵敏度较高，说明在这3 个频率附近的阻抗相角对kp的变化比较敏感；而1～40 Hz、54～1 000 Hz 频段的阻抗相角灵敏度曲线几乎与横轴重合，说明在这些频段kp的变化不会使阻抗相角产生明显变化。上述分析与kp变化时阻抗曲线发生变化的频段一致。

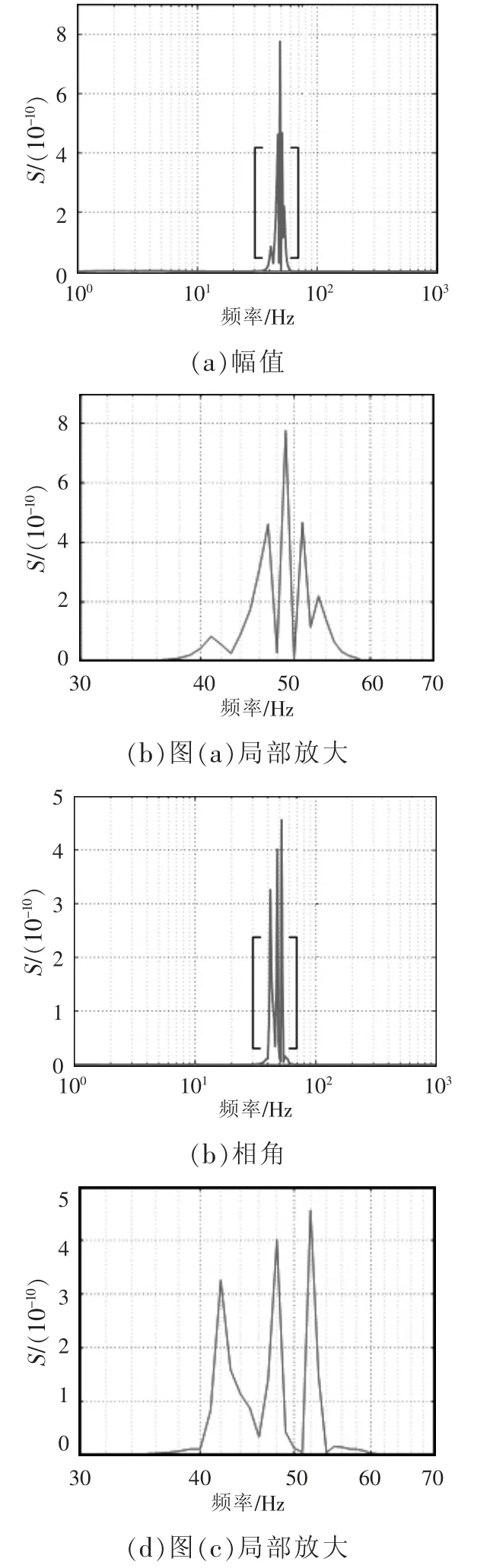
图7 kp 的阻抗灵敏度Fig.7 Impedance sensitivity of kp

阻尼系数D 的阻抗灵敏度如图8 所示，在频率为47、49、51 Hz 时幅值灵敏度曲线较高，说明在这3 个频率附近的阻抗幅值对D 的变化比较敏感；而1～36 Hz、60～1 000 Hz 频段的阻抗幅值灵敏度曲线几乎与横轴重合，说明在这些频段D 变化来使阻抗幅值明显变化；相角灵敏度在频率为42、48、52 Hz时较高，说明在这3 个频率附近的阻抗相角对D 变化比较敏感；而1～40 Hz、54～1 000 Hz 频段的阻抗相角灵敏度曲线几乎与横轴重合，说明在这些频段D 变化来使阻抗相角明显变化。上述分析与D 变化时阻抗曲线发生变化的频段一致。

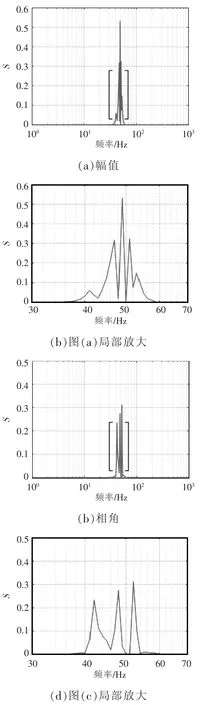
图8 D 的阻抗灵敏度Fig.8 Impedance sensitivity of D

虚拟转动惯量J 的阻抗灵敏度如图9 所示，幅值灵敏度曲线在频率为43、48、52 Hz 时较高，说明在这3 个频率附近的阻抗幅值对J 的变化比较敏感；而1～30 Hz、70～1 000 Hz 频段的阻抗幅值灵敏度曲线几乎与横轴重合，说明在这些频段J 的变化不会使阻抗幅值产生明显变化；相角灵敏度在频率为41、47 Hz 时较高，说明在这2 个频率附近的阻抗相角对J 的变化比较敏感；而1～30 Hz、60～1 000 Hz 频段的阻抗相角灵敏度曲线几乎与横轴重合，说明在这些频段J 的变化不会使阻抗相角产生明显变化。上述分析与J 变化时阻抗曲线发生变化的频段一致。

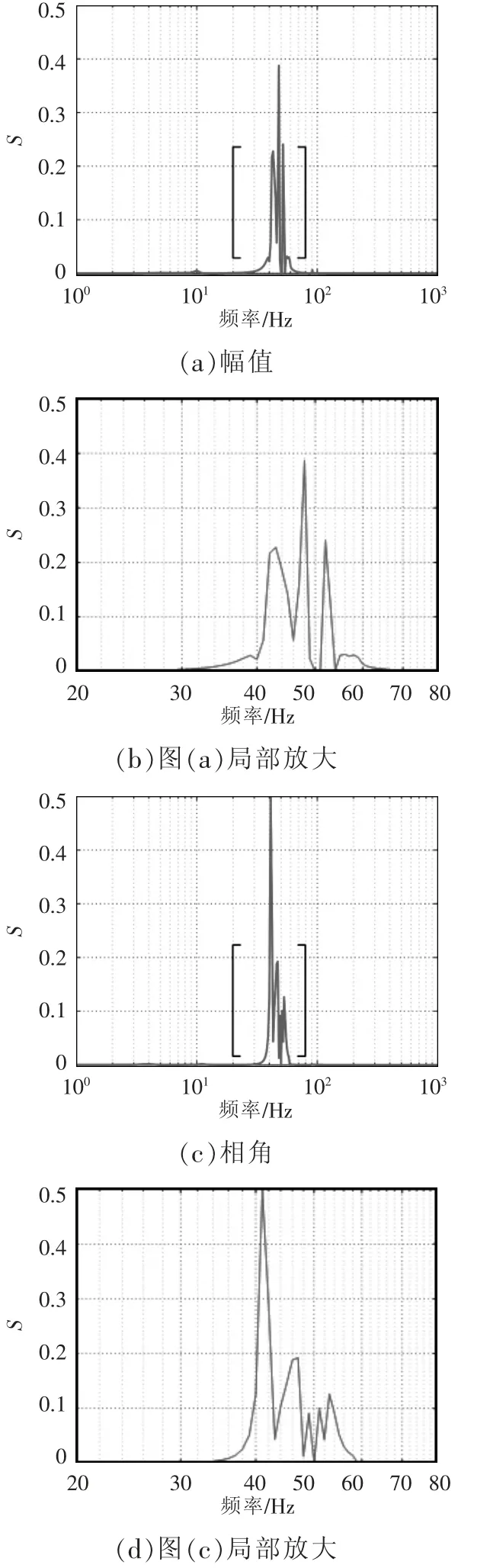
图9 J 的阻抗灵敏度Fig.9 Impedance sensitivity of J

3.2 稳定性分析

图10 为MMC 并网系统示意，MMC 和电网参数见表2。输电线路和变压器阻抗等效为电网阻抗，包括等效电网电感Lg1、Lg2和等效电网电容Cg。基于VSG 控制策略的MMC 可以视为电压源，此时MMC 并网系统的简化拓扑如图11 所示。

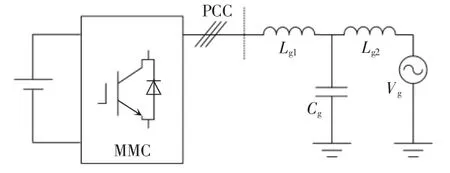
图10 MMC 并网系统示意Fig.10 Schematic of grid-connected MMC system

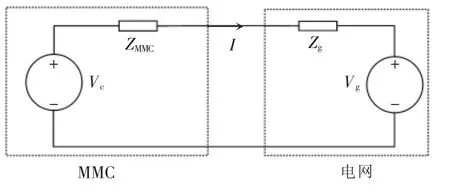
图11 MMC 并网系统简化拓扑Fig.11 Simplified topology of grid-connected MMC system

在图11 中，流过传输线路电流I 为

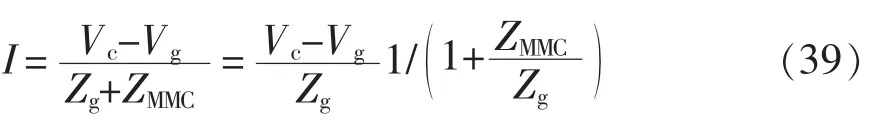
式中：Vc为VSG 策略下MMC 的等效电压源；Vg为电网电压；Zg为电网阻抗；ZMMC为MMC 交流端口小信号阻抗。在式（39）中，Vc和Vg是稳态量，而Zg是无源阻抗，因此（Vc-Vg）/Zg也是稳态量。此时系统稳定性取决于1/[1+（ZMMC/Zg）]。根据奈奎斯特稳定判据[10]，当MMC 和电网都是独立稳定的条件下，通过阻抗比ZMMC/Zg即可判断系统的稳定性。在MMC 与电网的阻抗交点图中，若MMC 与电网阻抗幅值交点对应的相角裕度较大，则系统是稳定的，若相角裕度很小，则系统将在该频率附近振荡，若相角裕度小于等于0°，则系统将发生振荡并发散。

图12 为MMC 阻抗与电网的阻抗伯德图。二者的幅频曲线在频率为32、89、92 和110 Hz 有交点，稳定裕度分别为11.1°、3.0°、165.8°和0.1°，其中，在110 Hz 稳定裕度很小，系统在110 Hz 附近将会振荡。

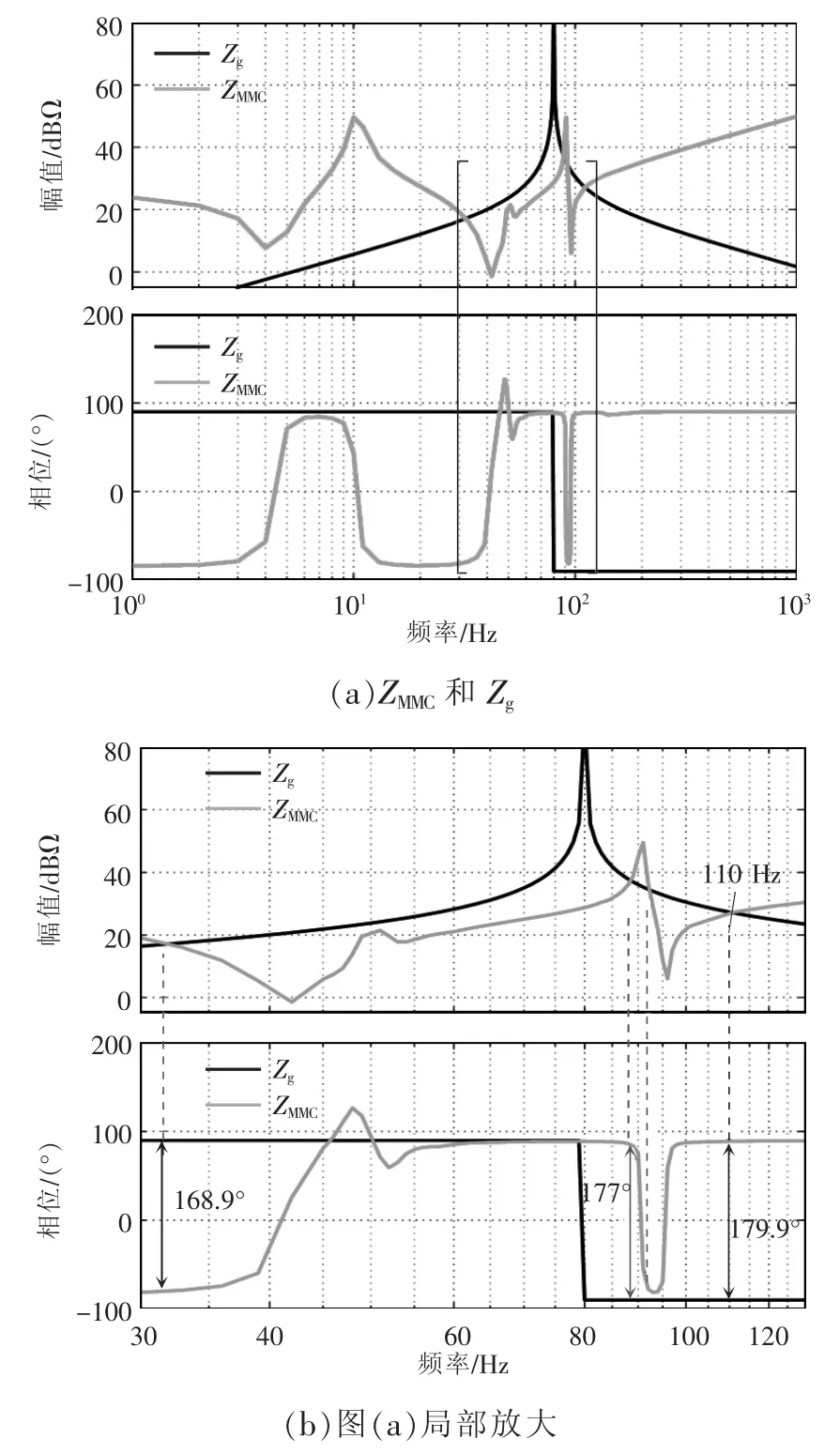
图12 MMC 并网系统中MMC 阻抗与交流电网阻抗Fig.12 MMC impedance and AC grid impedance in grid-connected MMC system

3.3 实验验证

通过硬件在环实验验证上述分析。硬件在环实验系统如图13 所示，主要由主计算机、目标机、DSP、I/O 卡和示波器等组成。首先在主计算机上用Matalab/Simulink 的工程模式进行编译，将代码下载到目标机中进行实时仿真（步长为25 μs）。目标机通过与其连接的多功能I/O 卡（型号Humusoft MF 624）与DSP 进行通信。包含环流抑制控制环节的VSG 控制策略在DSP（型号TMS320F28335）中单独运行，目标机中的实时模型生成的电压和电流信号通过嵌入在目标机器中的多功能I/O 卡适当放大并输出。利用示波器实时监测和记录目标机提供的电压和电流波形。PCC 点a 相电流实验波形如图14 所示。

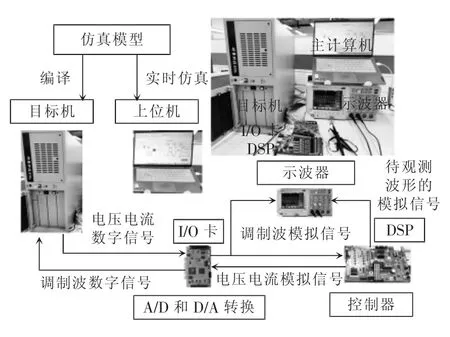
图13 硬件在环实验平台示意Fig.13 Schematic of hardware-in-the-loop experimental platform

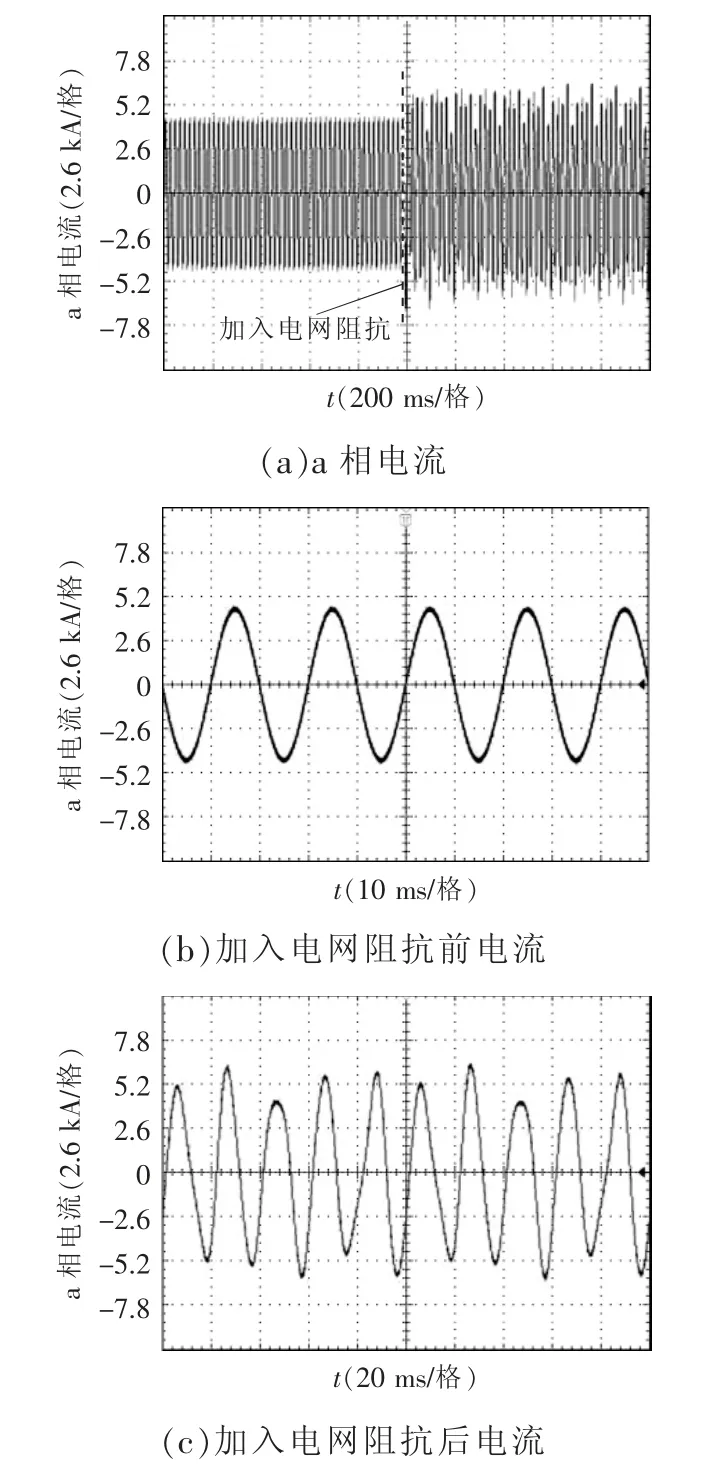
图14 PCC 点a 相电流实验波形Fig.14 Experimental waveforms of PCC current in phase a

由图14 可以看出，加入电网阻抗前，系统运行稳定，当2 s 加入电网阻抗后，PCC 点电流出现振荡，说明此时系统不稳定，对PCC 点a 相电流进行FFT 分析，结果如图15 所示。从频谱图可以看出，PCC 点a 相电流在110 Hz 处谐波含量大，这与图12 阻抗交点伯德图的分析结果一致，说明上述稳定性分析是正确的。

图15 PCC 点a 相电流谐波频谱Fig.15 Harmonic spectrum of PCC current in phase a

4 结论

（1）基于VSG 控制策略的MMC 的阻抗特性在低频段较为复杂，在容性和感性多次变化，高频段主要呈感性。

（2）VSG 控制参数中的虚拟转动惯量和阻尼系数对50 Hz 附近的MMC 阻抗有影响，有功-下垂系数较大时对50 Hz 附近的MMC 阻抗有比较明显的影响。

（3）当电网等效阻抗在高频段呈容性时，可能会与MMC 阻抗存在谐振点，导致MMC 并网系统在中高频段出现谐振现象。