弱电网条件下考虑频率耦合的三相并网逆变器简化阻抗建模及宽频带振荡分析

王海宁，陈燕东，廖书寒，伍文华，徐元璨，张 松

（湖南大学国家电能变换与控制工程技术研究中心，长沙 410082）

随着风能、太阳能等分布式电源DG（distributed generation）的快速发展，并网逆变器作为分布式电源和公用电网间的关键接口，将直流电能转换为高质量、高可靠的交流，在新能源发电系统中必不可少，但它仍然存在急需解决的问题：因控制系统设置不合理、电网强度变化等原因会引起并网逆变器输出阻抗与电网侧输出阻抗交互，易产生阻抗不匹配，导致输电系统发生振荡失稳，发生10～2 000 Hz 的宽频带振荡[1-3]。

学者们针对分布式供电系统中功率振荡问题提出了多种方法，并分析了系统失稳的原因。其中状态空间法和基于阻抗稳定性分析法是现阶段分析并网系统稳定性较重要的两种方法[4]。由于基于阻抗的稳定性分析法只用于建立各子系统阻抗模型，分析过程简单方便[5]。根据所建阻抗坐标系选择方法，现阶段阻抗分析方法主要有3 种：直流阻抗建模、交流阻抗建模和直流/交流混合阻抗建模，其中基于交流阻抗建模方法主要有：静止坐标系下序阻抗建模[6]、同步旋转坐标系下dq 阻抗建模[7-10]、极坐标系下广义阻抗建模[11]。序阻抗建模主要用谐波线性化方法建立阻抗模型[12]，并结合阻抗稳定性判据方法，研究系统稳定性。文献[13]指出在考虑频率耦合情况下，序阻抗建模和dq 阻抗建模等效，因此本文采用序阻抗建模的方法分析并网逆变器的稳定性问题。

文献[1]建立了直驱风电机组/双馈风电机组阻抗与控制器参数间的数学模型，但是在中低频情况下，没有考率频率耦合对所建阻抗模型的影响；文献[14]在考虑频率耦合的情况下，建立了并网逆变器的阻抗模型，但并没有根据各个控制参数对阻抗模型的影响，建立不同频段的简化阻抗模型。本文在直流侧接直流母线或储能装置，母线直流电压波动较小，直流侧影响可以忽略不计，根据不同控制参数对阻抗模型的影响，提出了宽频带的简化阻抗模型。文献[15]推导并验证了考虑多种频率耦合情况下的并网逆变器的频率耦合特性解析模型，但是所建多输入多输出MIMO（multi-input multi-output）的序阻抗矩阵对系统进行稳定性分析时比较复杂，本文在满足相同的相位裕度的条件下，建立了单输入单输出SISO（single input single output）序阻抗模型，并对系统稳定性进行了分析，最后提出了简化的阻抗模型。已有很多文献对宽频域振荡现象进行了研究。文献[16]将延时作为引起并网逆变器高频振荡的主要原因，并在单电流环和双闭环控制情况下进行了比较，得出了延时增加时，引起系统高频振荡时的极端频率点；文献[17]分析了风力发电场中长距离输电线路对并网逆变器高频振荡的影响，指出长距离输电线路是造成风电场输电系统不稳定的主要因素之一，并利用阻抗的方法进行了理论分析。在不同频段，产生功率振荡的原因也有很大区别，电网和变流器控制器之间的相互作用是次同步振荡现象的主要原因[18]，高带宽的锁相环可能引起系统相位裕度的降低，从而引起DFIG 系统的中频振荡[5]，但上述文献并没有分析不同控制器对于系统功率振荡问题的影响界限，针对不同频段的振荡问题，没有提出适用于当前频率范围的简化模型。

综上所述，在不同频率范围，影响系统稳定性因素不同，本文分别建立考虑频率耦合中低频段简化序阻抗模型和不考虑频率耦合高频段简化序阻抗模型，并根据不同控制环节特点，分频段讨论了不同控制环节对阻抗模型影响，明确了不同控制器对于系统稳定性影响界限，揭示了系统宽频带振荡产生原因。

1 并网逆变器SISO 序阻抗建模

图1 为本文所研究三相并网逆变系统结构，左侧为电网子系统，中间为逆变器子系统，右侧为直流母线。并网逆变器交流侧通过LC 滤波器在公共耦合点PCC（point of common coupling）接入电网，LC 滤波器由逆变器侧电感Lf和滤波电容Cf构成，Rd为Cf的寄生电阻，vdc为直流侧电压，uinv为逆变器侧输出电压，ug为电网电压，Zg为电网阻抗，ig为并网电流。

根据图1，当直流侧接直流母线或储能装置时，母线直流电压波动较小，直流侧影响可以忽略不计，所以本文所建并网逆变器阻抗模型没有考虑直流侧影响。在时域条件下，在没有中性点连接的三相平衡系统中，并网逆变器在静止坐标系下的平均模型[6]为

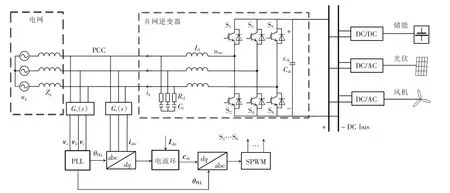
图1 三相并网逆变系统结构Fig.1 Structure of three-phase grid-connected inverter system

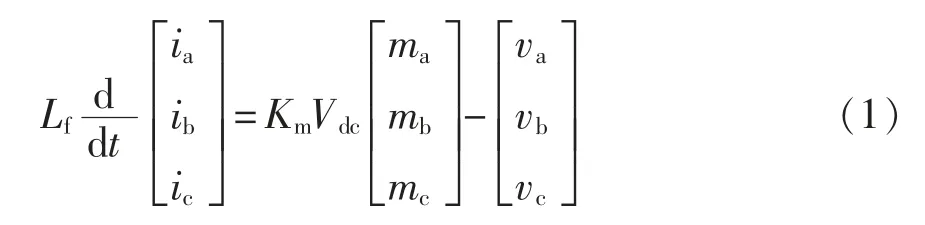
式（1）中：ia、ib、ic和va、vb、vc分别为PCC 点的电流采样值和电压采样值；ma、mb、mc为三相电压的调制信号；Km为调制增益；Vdc为直流侧电压幅值。

利用谐波线性化的方法，小信号平均模型式（1）可以转化到频域，用[f]表示为

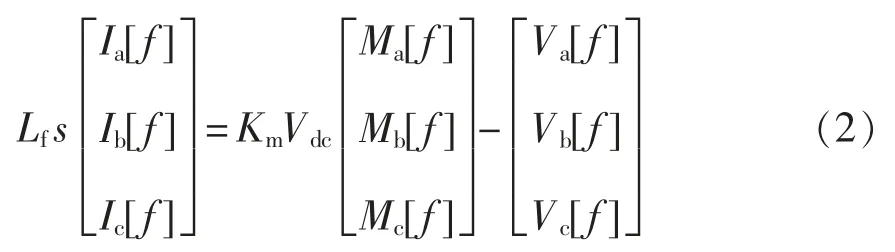
为推导并网逆变器序阻抗表达式，向并网逆变器交流侧注入频率为fp的正序电压扰动，按照逆变器产生频率耦合原理[19]，产生正序扰动电流和耦合负序扰动电流，其耦合关系见表1。

表1 电压扰动与电流响应分量频率耦合关系Tab.1 Frequency coupling relationship between voltage disturbance and current response component

忽略电网侧阻抗的影响，并网逆变器A 相输入电压在时域和频域条件下分别表示为

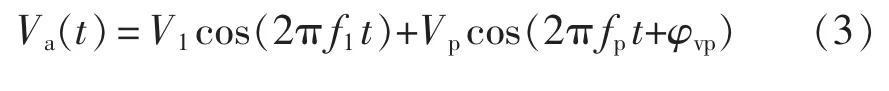
式中：V1和Vp分别为基频f1和扰动频率fp下的电压幅值；φvp为扰动电压的初相角；V±1=V1/2，

A 相电流和调制信号的频域表达式分别为

当频率为fp的扰动电压叠加在交流电压的输入侧会引起锁相环输出相位扰动，产生频率为fp-f1的扰动分量，在同步旋转坐标系下，id和iq计算为

将式（4）和式（5）代入式（6），应用频域卷积理论，id和iq的频域表达式为

式中，Gi（s）为电流采样滤波器的传递函数，Gi（s）=1/（1+sTi）。应用频域卷积理论，可得调制信号为

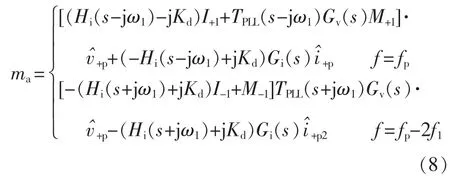
式中：TPLL（s）=HPLL（s）/[s+V1HPLL（s）] ；HPLL（s）=（KP_PLL+KI_PLL/s）/s 为锁相环的传递函数，KP_PLL和KI_PLL分别为锁相环的比例和积分增益；Hi（s）=KP_I+KI_I为电流环的开环传递函数，KP_I和KI_I分别为电流环的比例和积分增益；Kd为电压前馈系数；Gv（s）为电压采样滤波器传递函数，Gv（s）=1/（1+sTv）。将式（8）代入式（2）可得阻抗为

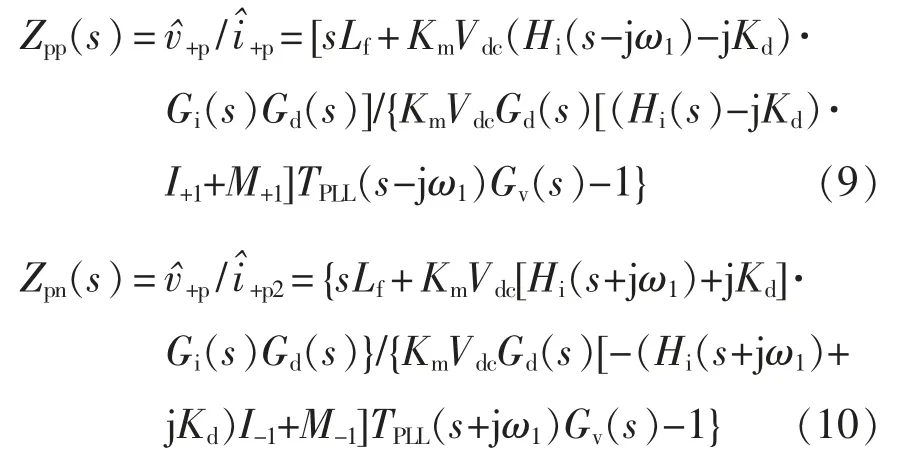
式中：Gd（s）为数字控制延时采用一阶帕德近似后的传递函数；M1为调制信号的基频分量。具体计算为

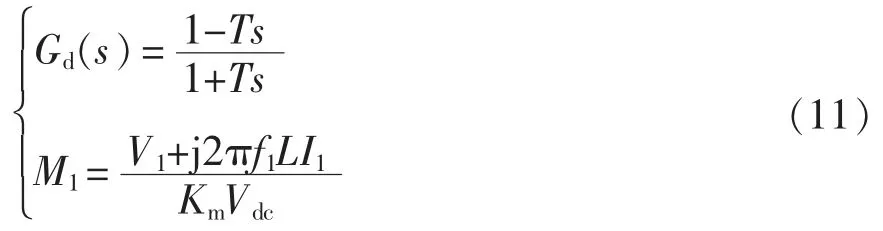
式中：T 为延时时间；I1为基频下的电流幅值。

根据变流器MIMO 系统的序阻抗矩阵元素之间的共轭关系，Znp（s）＝j2ω1），可得MIMO 序阻抗模型为

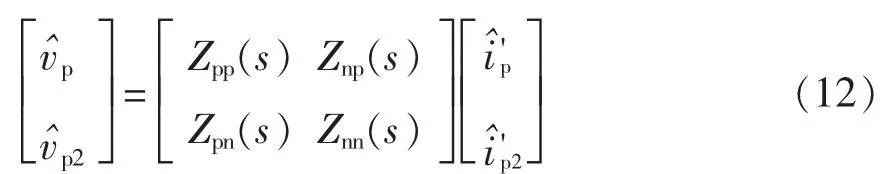
虽然可以根据MIMO 的序阻抗矩阵和广义奈奎斯特判据NSC（Nyquist stability criterion）对系统进行稳定性分析，但是分析过程比较繁琐，在满足相同的相位裕度的条件下，MIMO 序阻抗模型可以转化为单输入单输出SISO 序阻抗模型[20]，可简化逆变器和电网之间的交互稳定性分析。SISO 序阻抗模型定义为

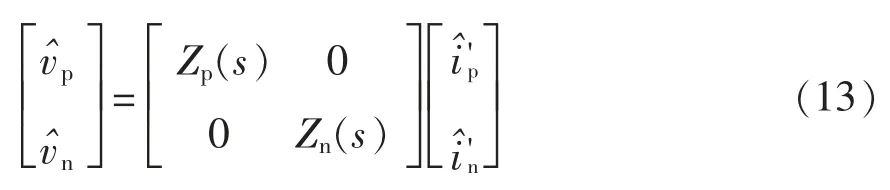
式中：Zp（s）和Zn（s）分别为逆变器的正序和负序阻抗；和分别为注入的负序扰动电压和负序电流响应。根据序阻抗的共轭关系和式（13），可得逆变器的正负序阻抗为

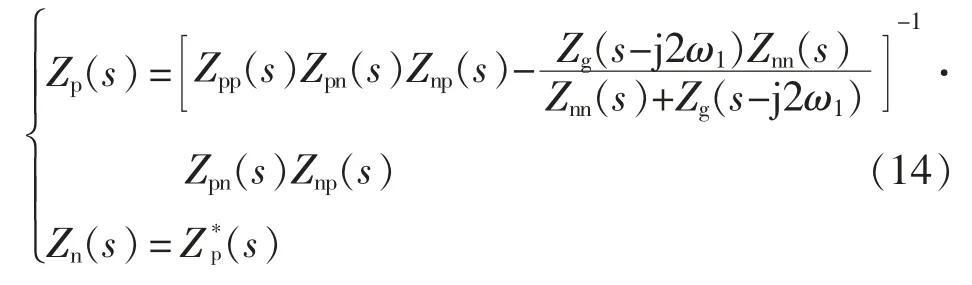
根据推导的考虑频率耦合情况下的并网逆变器序阻抗模型，可以通过仿真验证其准确性，如图2 所示。可知在中低频段考虑频率耦合的阻抗模型和高频区的简化阻抗模型理论和仿真结果高度一致，这为后面的宽频带振荡分析提供了理论依据。

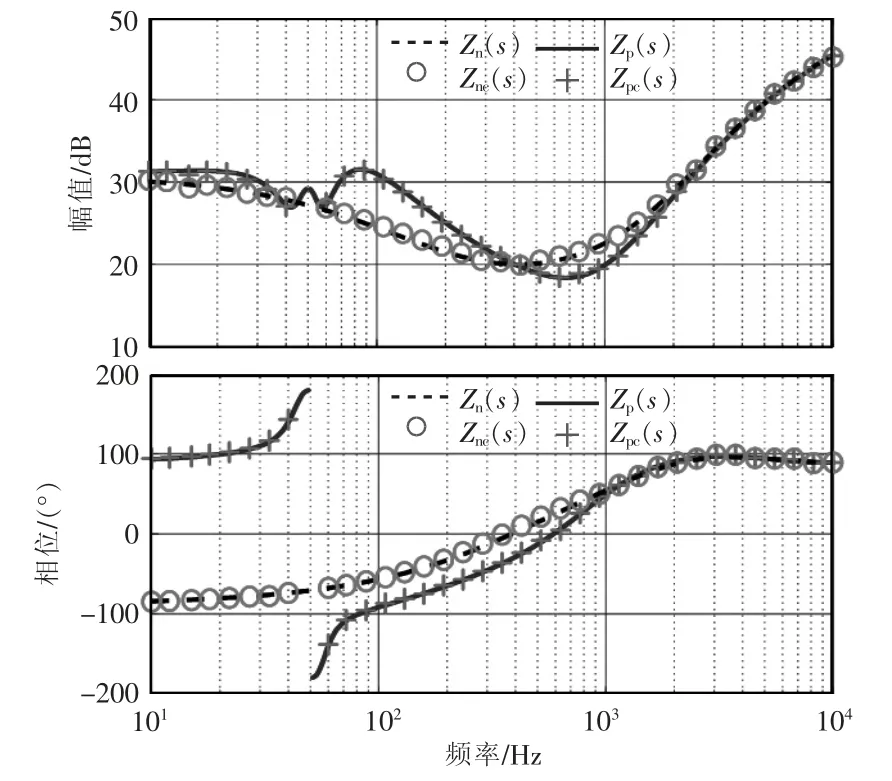
图2 三相并网逆变系统的阻抗模型验证Fig.2 Verification of impedance model of three-phase grid-connected inverter system

2 并网逆变器系统宽频带稳定性

由于电力电子装置的本体控制系统涉及多个不同控制带宽的控制器协调配合，不同控制器之间也会发生耦合，导致各种不同频段的功率振荡。在不同频段，发生功率振荡的原因不相同，本节将振荡现象按照不同频段，分别进行分析，考虑到正负序阻抗之间的共轭关系，为了简化分析，只考虑正序阻抗下不同控制环节对系统功率振荡的影响。

2.1 锁相环对阻抗特性的影响

为方便计算，根据文献[7]可将正序阻抗与负序阻抗中的锁相环闭环传递函数统一为TPLL（s），即

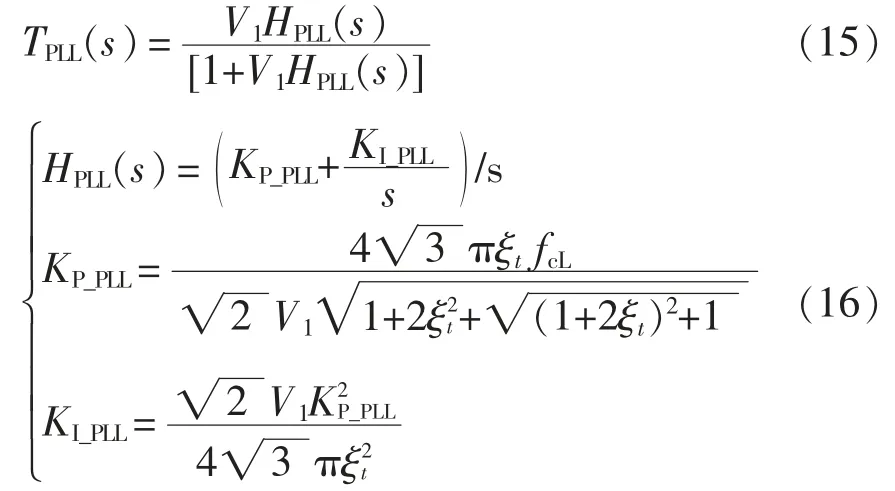
式中，KP_PLL和KI_PLL为锁相环控制参数，由典型II型系统的控制器设计方法[21]可到；fcL为锁相环控制带宽。由式（16）可知，通过选取不同的控制带宽fcL和阻尼比ξt可以得到不同的锁相环控制特性，进而设计阻抗特性。

将式（15）表示为二阶系统的形式，有

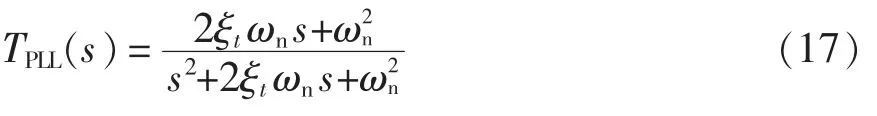
式中，ξt、ωn分别为锁相环的阻尼系数和自然频率。

根据式（16）、式（17）、式（14）可得考虑频率耦合情况下的逆变器序阻抗模型，将阻尼比ξt设为0.707，控制带宽分别取10、20、30 和40 Hz，分析锁相环控制带宽对逆变器阻抗特性的影响，如图3 所示。

由图3 可见，在（f1-fcL）～（f1+fcL）区间内并网逆变器阻抗特性主要受fcL的影响，在（f1-fcL）～f1频段内，阻抗相角大于90°，呈现感性负阻尼特性；在f1～（f1+fcL）频段内，阻抗相角小于-90°，呈现容性负阻尼特性，且当fcL改变时，阻抗幅值在f1-fcL和f1+fcL处出现谐振峰，将fcL固定为20 Hz，ξt分别取0.34、0.71、0.85 和0.98，分析锁相环阻尼比对阻抗的影响，可得阻抗曲线如图4 所示。由图4 可见，ξt主要影响频率在（f1-fcL）和（f1+fcL）处谐振峰的凹陷程度。

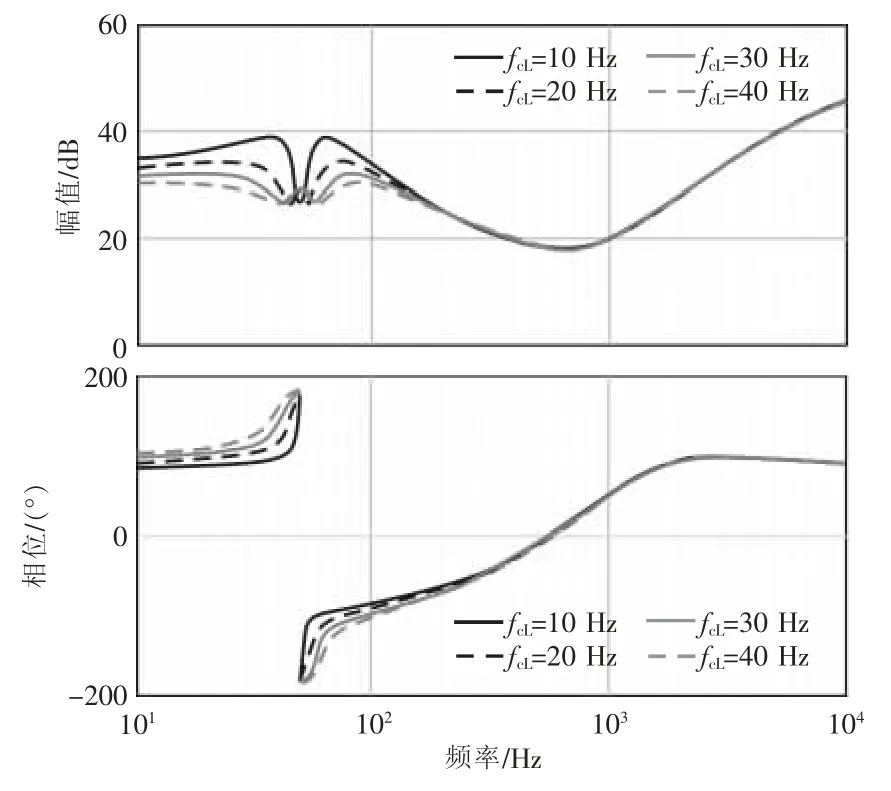
图3 锁相环带宽fcL 对阻抗特性的影响Fig.3 Influence of PLL bandwidth fcL on impedance characteristics

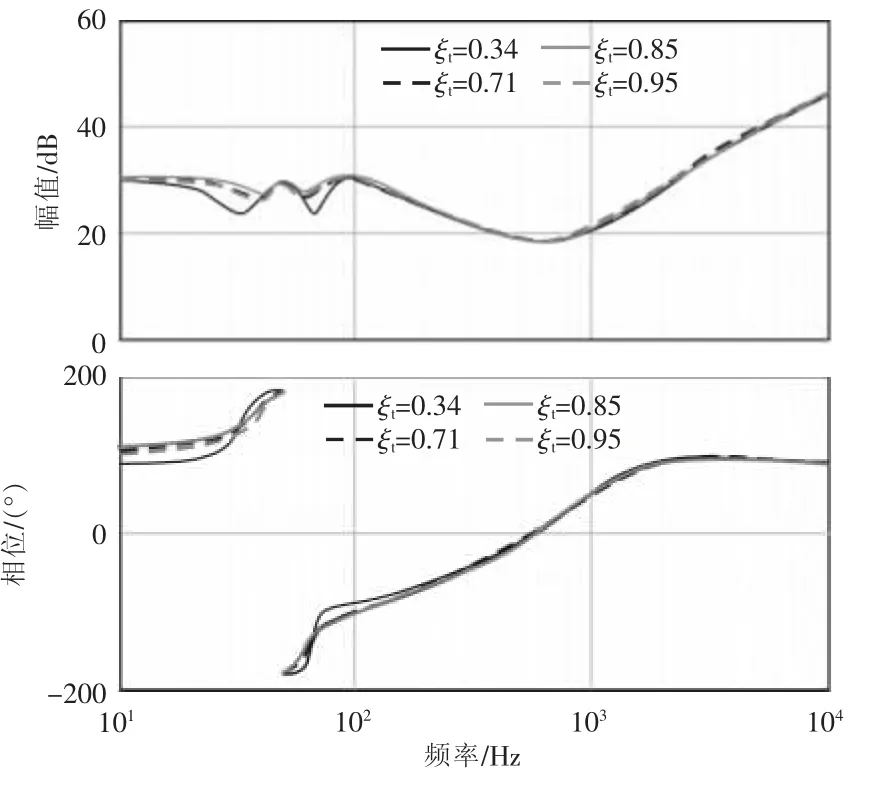
图4 锁相环阻尼比ξt 对阻抗特性的影响Fig.4 Influence of PLL damping ratio ξt on impedance characteristics

为进一步分析锁相环参数对并网逆变系统稳定性的影响，基于阻抗比的奈奎斯特稳定性判据用于分析系统的稳定性。并网逆变系统的阻抗比为

根据式（18）可得，锁相环参数变化时，并网逆变系统阻抗比的奈奎斯特图如图5 所示。由图5 可见，锁相环带宽对系统的稳定性产生很大影响，带宽越宽，系统稳定性差；而锁相环阻尼比对系统稳定性影响较小。

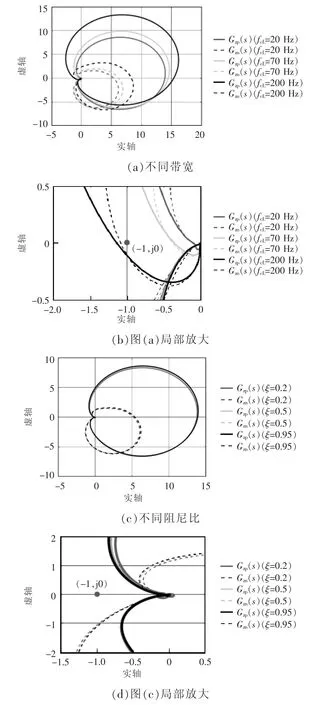
图5 锁相环不同参数下式（24）的奈奎斯特图Fig.5 Nyquist diagram of Eq.（24）with different PLL parameters

2.2 电流环对阻抗特性的影响分析

电流环控制器的闭环传递函数为

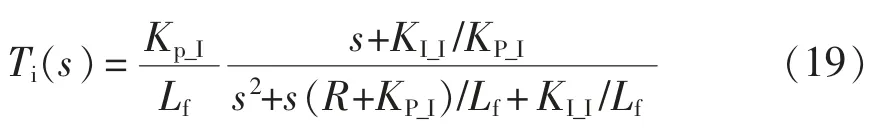
将式（19）表示为二阶系统形式，即

式中：ξi为电流环阻尼比；ωn为自然频率。根据典型II 型系统的控制器设计方法可得

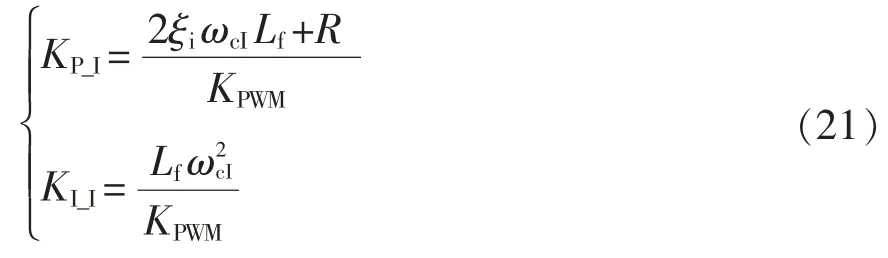
式中：ωcI=2πfcI；fcI为电流环控制带宽；KPWM为桥路PWM 等效增益。

将fcL固定为10 Hz，ξi固定为0.707，fcI分别取100、200、300 和400 Hz，分析fcI对阻抗的影响，阻抗曲线如图6 所示。将fcL固定为10 Hz，fcI固定为200 Hz，ξi分别取0.34、0.51、0.75 和0.98，分析电流环阻尼比对阻抗的影响，阻抗曲线如图7 所示。

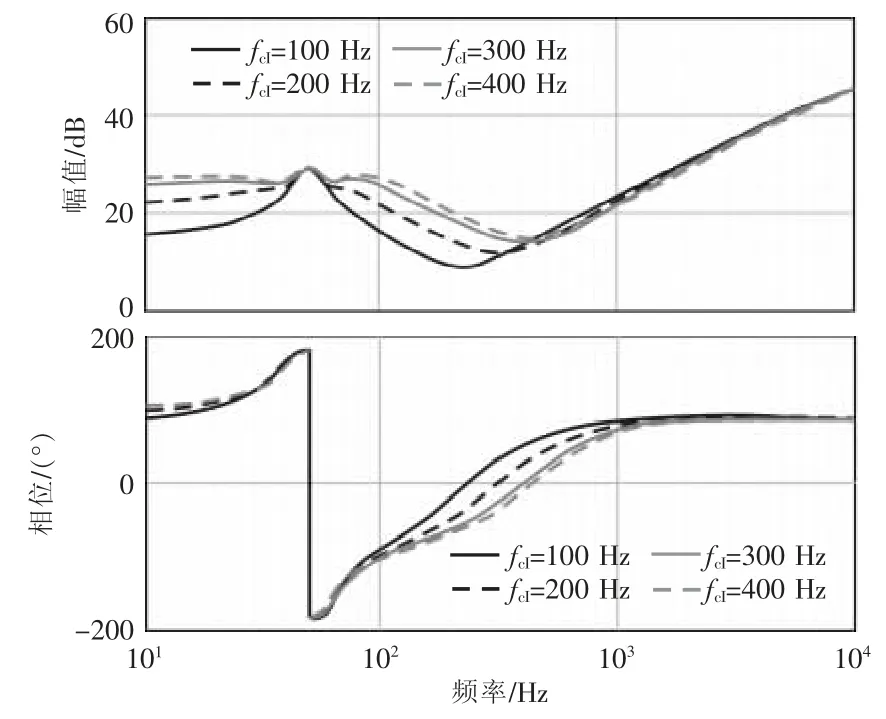
图6 电流环带宽对阻抗特性的影响Fig.6 Influence of current loop bandwidth on impedance characteristics

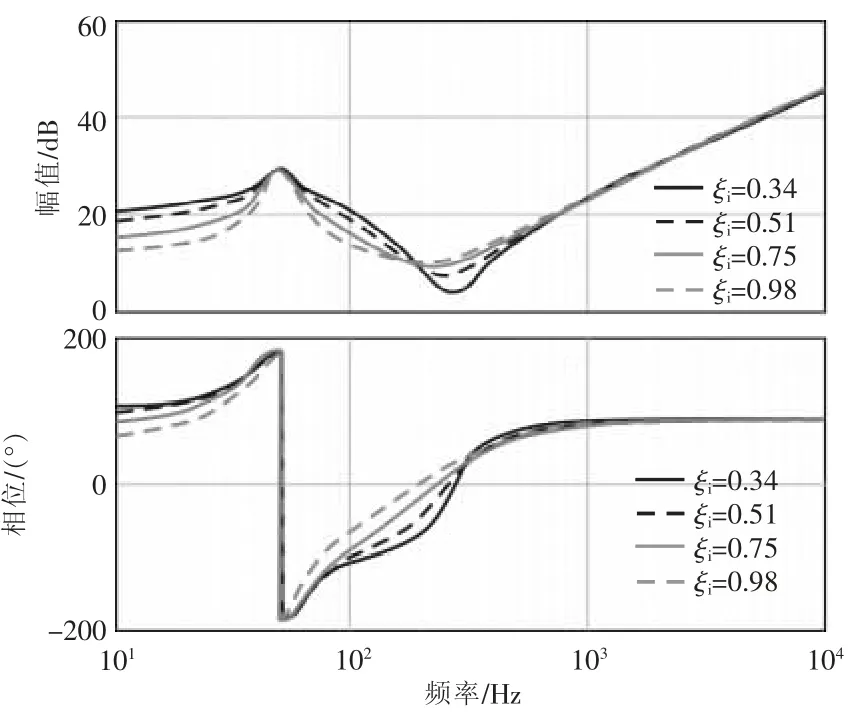
图7 电流环阻尼比对阻抗特性的影响Fig.7 Influence of current loop damping ratio on impedance characteristics

由图6 可知，在0～（f1-fcI）频段内，随着fcI的增大，逆变器阻抗幅值逐渐增大，相位基本保持不变；在（f1+fcL）～（f1-fcI）频段内，随着fcI的增大，逆变器阻抗幅值逐渐增大，相位随频率的增加而逐渐由负变正。由此可知，在频段0～（f1-fcL）和（f1+fcL）～（f1-fcI）内，并网逆变器的阻抗特性主要受fcI的影响。

由图7 可知，在0～（f1-fcL）频段内，随着ξi的增大，阻抗幅值和相位逐渐增大；在（f1+fcL）～（f1+fcI）频段内，随着ξi的减小，逆变器阻抗阻尼特性减弱，幅值相角更接近-90°，谐振峰在（f1+fcI）频率处的凹陷程度增大。可知电流环阻尼比ξi主要对0～（f1-fcL）和（f1+fcL）～（f1-fcI）频段内的阻抗特性产生影响。

根据式（18）可得，电流环参数变化时，并网逆变系统阻抗比的奈奎斯特图如图8 所示。

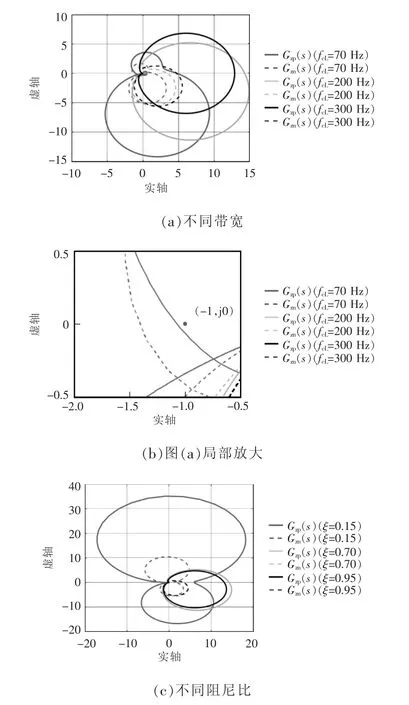
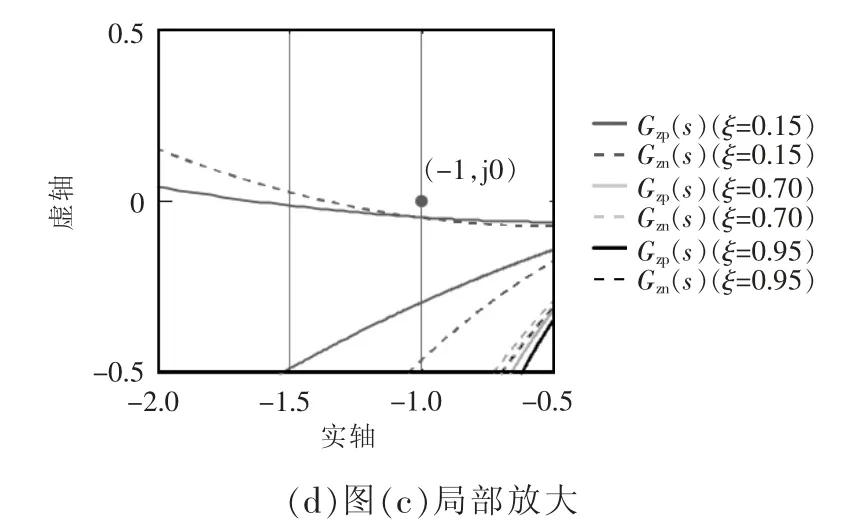
图8 电流环不同参数下式（24）的奈奎斯特图Fig.8 Nyquist diagram of Eq.（24）with different current loop parameters

2.3 控制系统延时对阻抗的影响分析

延时分别取20、70、120 μs，可得高频情况下逆变器序阻抗的伯德图如图9 所示。由图9 可见，在f＞（f1+fcI）的频段，随着延时的增加，阻抗幅值曲线部分出现一个凹槽，相位也出现明显变化，说明延时对逆变器的阻抗特性产生重要影响。图10 为不同延时下系统的阻抗比奈奎斯特图，可见随着延时的增加，系统逐渐趋于失稳。

图9 数字控制延时对阻抗特性的影响Fig.9 Influence of digital control delay on impedance characteristics

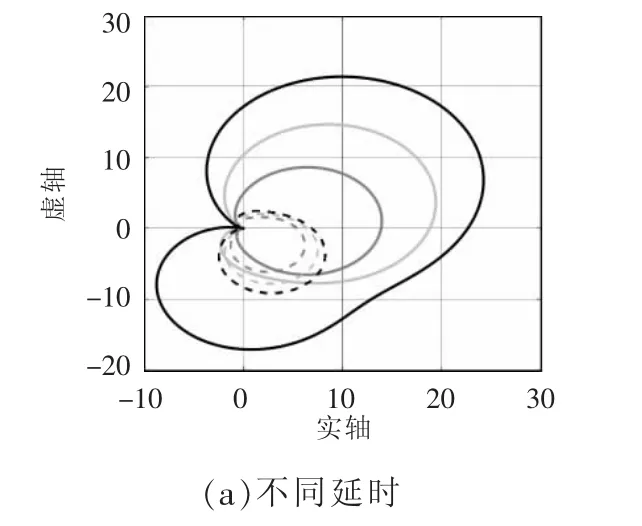
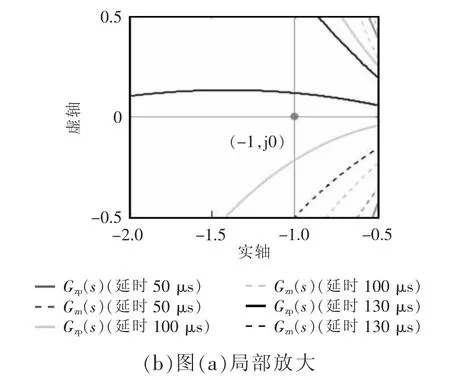
图10 不同延时条件下式（24）的奈奎斯特图Fig.10 Nyquist diagram of Eq.（24）under different delay conditions

综上所述，可将并网逆变器宽频带阻抗特性划分为4 个频段：0～（f1-fcL）为频段I，（f1-fcL）～（f1+fcL）为频段Ⅱ，（f1+fcL）～（f1+fcI）为频段Ⅲ，f＞（f1+fcI）为频段Ⅳ。

3 并网逆变器简化阻抗模型

由上述分析可知，在不同频率范围内，各个控制环节对阻抗特性曲线的影响也不同，在中低频段（10～800 Hz）时，锁相环和电流环对系统稳定性的影响起主要作用，在高频段（＞800 Hz），延时对系统稳定性的影响起主要作用。因此在考虑频率耦合的情况下，根据不同控制环节对于系统稳定性的影响界限，可对系统的阻抗模型进行简化。

3.1 考虑频率耦合的中低频段简化模型

在中低频段，延时对阻抗特性曲线的影响较小，在分析系统中低频段功率振荡时，可忽略延时的影响，建立简化的序阻抗模型，阻抗可简化为

3.2 考虑数字控制延时的高频段模型

由于延时主要对系统高频段稳定性产生影响，在分析系统高频段振荡现象时，为了简化分析，只需要建立在高频情况下的阻抗模型。在高频情况下，频率耦合现象和锁相环的影响可以忽略不计，即锁相环增益近似为0。考虑延时的情况下，并网逆变器序阻抗模型在高频段可简化为

为了验证所提简化模型的正确性，将前面推导的详细模型和简化模型进行了对比，如图11 所示可见，简化模型与详细模型吻合良好，误差在可接受范围，验证了简化模型的适用性。

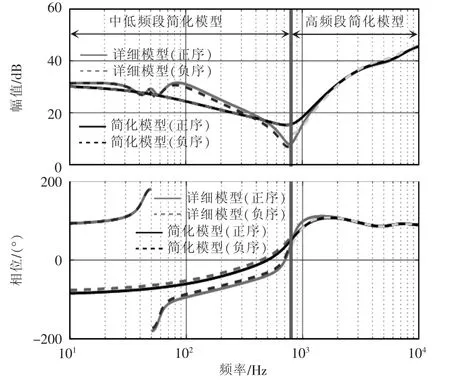
图11 详细模型与简化模型对比Fig.11 Comparison between detailed and simplified models

4 实验验证

为了验证本文所提宽频带建模方法的有效性，搭建了10 kW 三相逆变并网系统的实验平台，如图12 所示。并网逆变系统的参数见表2，控制系统通过DSP TMS320F2812 实现对逆变器的功率控制，直流侧采用整流器实现直流电压的稳定控制，逆变器开关频率设置为10 kHz，通过利用高速A/D 采样芯片ADS8556 实现对电压电流的采样，逆变器d 轴电感电流参考值为21 A，q 轴电感电流参考值设为0 A，保证了系统的高功率因数运行。

表2 VSI 并网逆变系统参数Tab.2 Parameters of VSI grid-connected inverter system

图12 三相并网逆变器实验平台Fig.12 Experimental platform of three-phase gridconnected inverter

4.1 锁相环参数的影响

图13 显示了锁相环参数改变后PCC 点电感电流实验波形，令电流环带宽fcI=300 Hz，短路比SCR=3，可知，锁相环带宽fcL=20 Hz 时并网逆变系统稳定运行，当锁相环带宽fcL=80 Hz 时系统出现功率振荡现象，并网电感电流产生100 Hz 和200 Hz 附近的功率振荡，理论和实验结果高度一致。

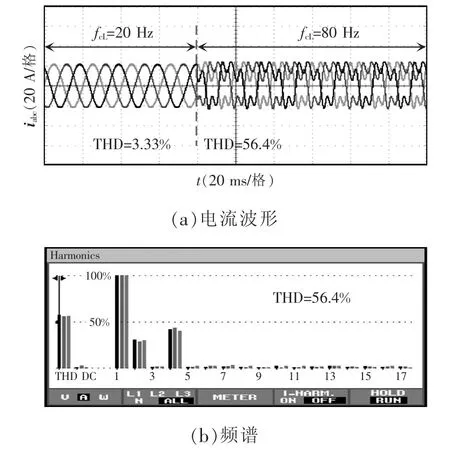
图13 锁相环参数改变时并网电感电流和频谱Fig.13 Grid-connected inductor current and its spectrum under changes in PLL parameters

4.2 电流环参数的影响

图14 显示了电流环参数改变后PCC 点电感电流实验波形，令锁相环带宽fcL=30 Hz，短路比SCR=3，可知，电流环带宽fcI=200 Hz 时并网系统稳定运行，当电流环带宽fcI=1 000 Hz 时系统出现功率振荡现象。

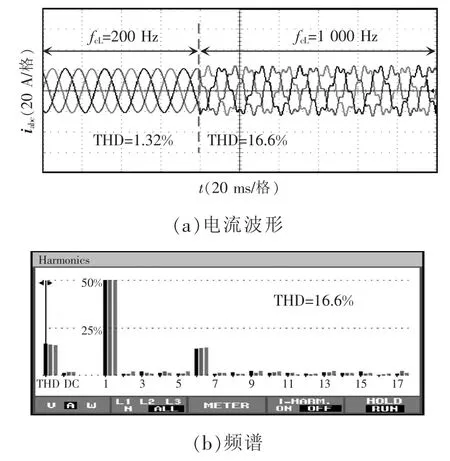
图14 电流环参数改变时并网电感电流和频谱Fig.14 Grid-connected inductor current and its spectrum under changes in current loop parameters

4.3 延时对系统的的影响

图15 显示了延时改变后PCC 点电感电流实验波形，可知，当锁相环带宽fcL=30 Hz，电流环带宽fcI=240 Hz，短路比SCR=3，延时=10 μs 时并网系统稳定运行，随着延时的增大，延时为150 μs 时系统电感电流出现1 300 Hz 和1 400 Hz 附近的高频振荡，理论和实验结果高度一致。

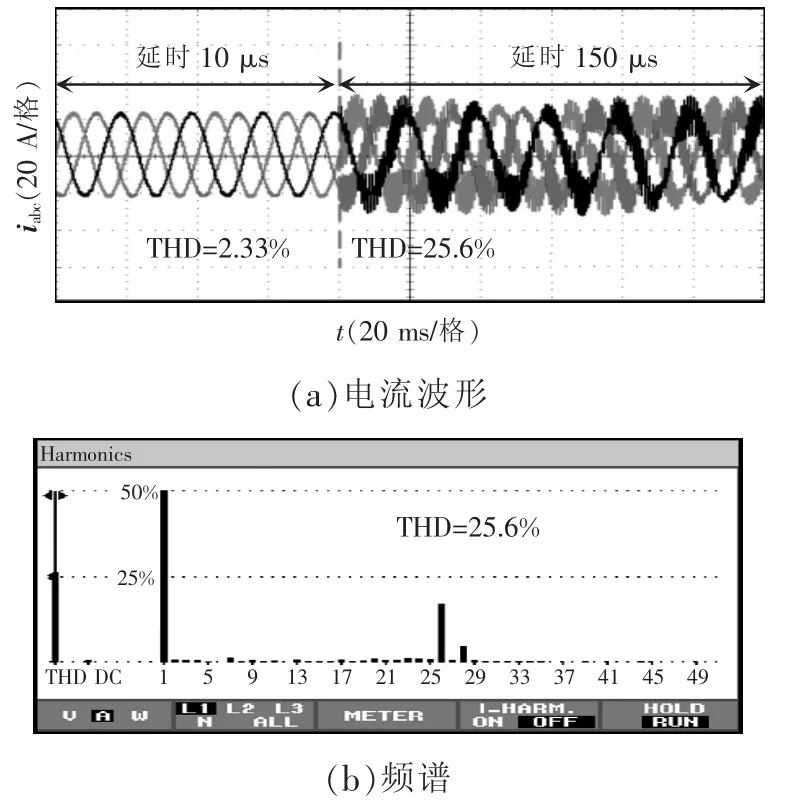
图15 延时改变时并网电感电流和频谱Fig.15 Grid-connected inductor current and its spectrum when delay changes

5 结论

（1）根据锁相环、电流环和延时对并网逆变器阻抗特性的影响，可将并网逆变器的阻抗特性划分为4 个频段。在0～（f1-fcL）频段内，阻抗特性呈现感性，由锁相环和电流环共同主导；在（f1-fcL）～（f1+fcL）频段内，基频左侧为感性负阻尼，右侧为容性负阻尼，主要由锁相环主导；在（f1+fcL）～（f1+fcI）频段内，随着电流环带宽的增大，在阻抗幅值增大的同时，呈现电容特性的区域增大，主要由电流环主导；在f＞（f1+fcI）频段内，已经超出锁相环的控制带宽，锁相环增益近似为0，可以忽略锁相环的影响，延时对阻抗特性的影响较大。

（2）在中低频段，延时对阻抗特性的影响较弱，在分析中低频段振荡问题时，可以忽略延时的影响，建立考虑频率耦合的简化模型；在高频段，已经超出锁相环控制带宽，可以省略锁相环的作用，考虑延时的影响，建立高频段的简化阻抗模型，用以分析高频段振荡问题。