双馈异步发电机序阻抗建模简化方法

李 飞，温世全，张永新，马铭遥，张 兴

（合肥工业大学电气与自动化工程学院，合肥 230009）

随着太阳能、风能等新能源发电所占比例逐年提高，电力电子设备作为与电网的接口装置被广泛应用[1]。与传统发电方式相比，新能源发电具有宽频带动态响应显著的特点[2]。因此，电力电子设备之间及其与电网之间相互作用易产生宽频振荡问题，严重影响电网的设备安全、用电质量以及系统稳定性，对新能源发电的应用带来巨大挑战[3]。

阻抗分析法在新能源发电系统并网稳定性分析和谐振分析方面具有优越性，已得到了广泛应用[4-5]。阻抗分析法常用的阻抗模型是基于谐波线性化的序阻抗，通过向待求解系统注入不同频率、不同相序的电压扰动，计算对应频率的电流响应，进而得到系统的序阻抗模型[6-7]。序阻抗模型具有明确的物理意义，可直接测量。此外，该方法还可用于各种复杂情形下的系统建模和分析[8]，是当前的研究热点。

目前已有学者对双馈异步发电机DFIG（doubly-fed induction generator）的序阻抗模型进行研究。文献[9]建立DFIG 的序阻抗模型，并分析了锁相环PLL（phase-locked loop）、电流环的参数对阻抗模型的影响，指出PLL 对阻抗特性影响较大；文献[10]建立考虑频率耦合的DFIG 序阻抗模型，表明锁相环和转子电流不对称控制是产生频率耦合的原因。上述文献对DFIG 进行序阻抗建模均采用电机的电压和磁链方程，运算较复杂。为此，有学者提出采用电机等效电路进行建模的方法。文献[11]采用电机等效电路对DFIG 进行序阻抗建模，建模过程得以简化；文献[12]将此方法用于频率耦合的研究，分析DFIG 通过直流母线的耦合关系。但是，采用电机等效电路建模时忽略了励磁支路，文献[11]通过仿真分析了励磁支路对阻抗模型影响，但只针对特定情形，不能推广至一般情况。因此，有必要采用计及励磁支路的电机等效电路对DFIG 进行序阻抗建模，分析两种模型之间的差异并明确简化模型的使用条件。

本文在采用电机等效电路对DFIG 进行序阻抗建模时考虑了励磁支路的影响，利用谐波线性化方法得到了DFIG 转子侧的序阻抗模型，并通过仿真验证了所建模型的准确性。在此基础上对比分析了其与简化模型的差异，结果表明在不同的PLL 带宽、电流环带宽和运行工况条件下，忽略励磁支路的简化建模方法对DFIG 转子侧的序阻抗模型影响很小。

1 系统描述

DFIG 的结构如图1 所示。通过L 滤波器与电网相连的变换器称为网侧变换器GSC（grid-side con-verter），与异步电机转子相连的变换器称为转子侧变换器RSC（rotor-side converter），异步电机定子与电网相连，GSC 与RSC 通过直流母线相连。通常认为直流母线电容足够大，直流环节可作为理想的直流电压源。基于这一假设，GSC 与RSC 之间解耦，DFIG 的阻抗可表示为GSC 阻抗与RSC 阻抗的并联。GSC 阻抗建模与并网逆变器相同，故本文重点研究RSC 阻抗建模。

图1 双馈异步发电机的结构Fig.1 Structure of DFIG

1.1 RSC 的主电路

RSC 的主电路是异步电机，序阻抗建模时可采用电机的电压和磁链方程或等效电路。以等效电路进行建模较简单，但是现有的序阻抗模型未计及励磁支路。因此，本文的建模采用如图2 所示的计及励磁支路的电机等效电路。

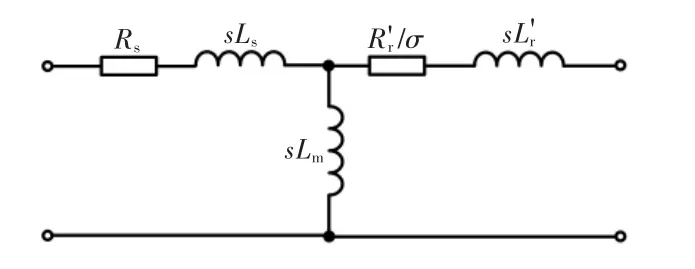
图2 计及励磁支路的异步电机等效电路Fig.2 Equivalent circuit of induction motor with excitation branch

图2 中，Rs和Ls为定子电阻和定子漏感；Lm为励磁电感；σ 为用于频率归算的转差率；和为绕组归算后的转子电阻和转子漏感，可表示为

式中：Rr和Lr为转子电阻和转子漏感；Ke为定转子匝比。式（1）表示转子电阻和漏感的绕组归算。

1.2 RSC 的控制回路

RSC 的控制回路包括一个快速的dq 电流内环和一个较慢的功率外环。RSC 的功率外环通过改变d 轴和q 轴电流参考值来控制DFIG 输出的有功和无功功率，因为其控制带宽较低，所以认为电流参考值是恒定的。RSC 的控制框图如图3 所示。图3 中，ira、irb、irc和mra、mrb、mrc分别表示三相坐标系下的转子电流和RSC 调制信号；ird、irq和mrd、mrq分别表示dq坐标系下的转子电流和RSC 调制信号，ird和irq表示转子电流的d、q 轴参考值，恒定不变；θPLL表示PLL输出角度，θm表示电机转子机械角度，两者之差将用于转子电流的Park 变换。电流控制方式为PI 控制，Krp和Kri分别为电流环比例系数和积分系数，Krd为解耦增益，则RSC 电流环传递函数Hri（s）表示为

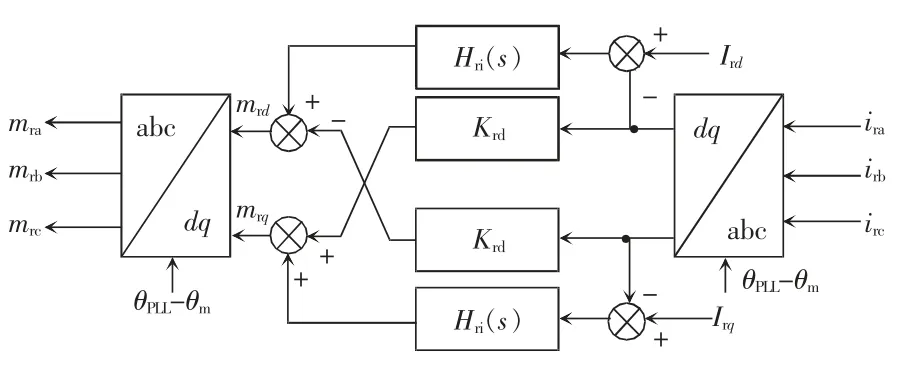
图3 RSC 电流环控制框图Fig.3 Block diagram of RSC current loop control

PLL 用于获得定子电压相位，本文采用应用最广泛的单同步坐标系锁相环SRF-PLL（synchronous reference frame phase-locked loop），其控制框图如图4 所示。

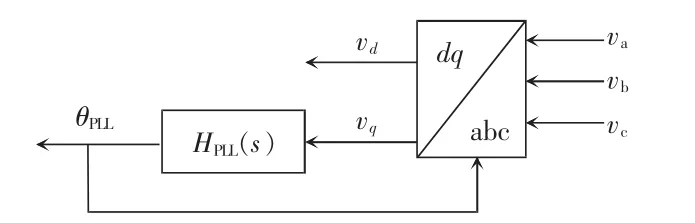
图4 锁相环控制框图Fig.4 Block diagram of PLL control

图4 中，va、vb和vc为三相坐标系下的定子电压；vd和vq为dq 坐标系下的定子电压；HPLL（s）为q 轴电压和PLL 输出角度θPLL之间的传递函数，表示为

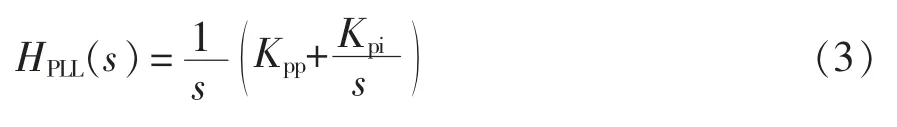
式中，Kpp和Kpi分别为PLL 的比例系数和积分系数。可知，RSC 的控制回路与并网逆变器类似，但主电路除了增加绕组归算和频率归算外，还需计及励磁支路。

2 阻抗建模

针对图1 所示的RSC 电路，在定子电压注入频率为fp的正序电压扰动，定子电流将产生相同频率fp的正序响应；注入频率为fn的负序电压扰动，定子电流将产生相同频率fn的负序响应；电压扰动与同频率电流响应之比即为序阻抗。因此，对RSC的序阻抗建模可分为3 步：首先通过RSC 主电路即异步电机等效电路得到扰动频率下定、转子之间的电压、电流关系；然后通过RSC 控制电路得到扰动频率下转子电压、电流之间的关系；最后将上述结果进行整理化简，即得RSC 的序阻抗模型。

2.1 主电路建模

以a 相为例，根据如图5 所示的异步电机小信号等效电路，分析定、转子之间电压、电流的关系。这一步是RSC 序阻抗建模不同于并网逆变器之处，也是本文以计及励磁支路的等效电路进行序阻抗建模的基础。和

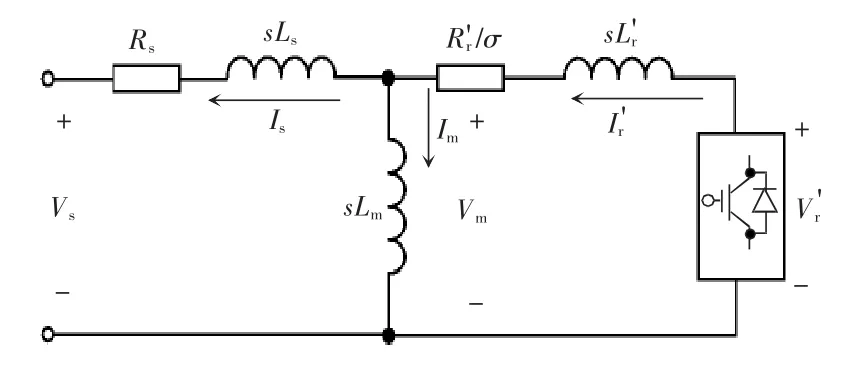
图5 异步电机小信号等效电路Fig.5 Small-signal equivalent circuit of induction motor

图5 中，电压、电流均为小信号，Vs和Is表示定子端口某一频率的正序或负序电压扰动和电流响应；Vm和Im表示励磁电压和励磁电流；表示经过绕组归算和频率归算的转子电压和转子电流。归算前后转子电压、电流的关系表示为

式中，Vr和Ir为归算前的转子电压和转子电流。需要注意的是，转差率与电压扰动的相序和频率有关，不同频率正负电压扰动对应的转差率为

式中：σp（s）和σn（s）为正序和负序电压扰动对应的转差率；ωm为电机转子机械角频率。

根据图5 所示等效电路，不考虑励磁支路时，得到电路方程为

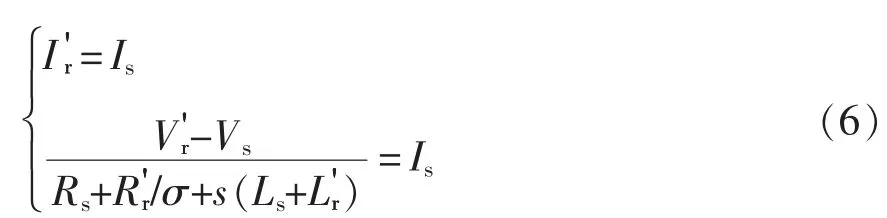
考虑励磁支路时，得到电路方程为

2.2 控制回路建模

根据图3 所示RSC 电流环控制框图和图4 所示PLL 控制框图可知，调制信号与转子电流、PLL输出相角有关，且PLL 输出相角与定子电压有关。因为调制信号经过SPWM 产生转子电压，故控制回路建模的目的就是建立转子电压响应和定子电压扰动、转子电流小信号之间的传递函数。

2.2.1 锁相环建模

定子电压注入电压扰动，转子电流将产生相应的电流响应。RSC 电流环建模过程与并网逆变器相同，但需要特别注意转子侧与定子侧在频率上的差异。假设注入正、负序电压扰动后a 相转子电流的时域表达式为

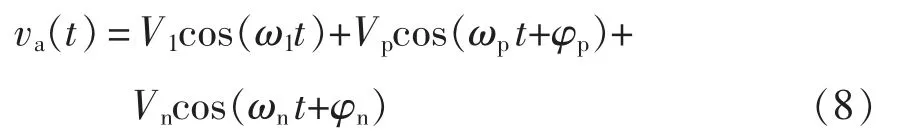
式中：V1、Vp和Vn为电压基波、正序电压扰动和负序电压扰动的幅值；ω1、ωp和ωn为电压基波、正序电压扰动和负序电压扰动的角频率，与之对应的频率为f1、fp和fn，其他变量也采用相同的对应关系；φp和φn为正序电压扰动和负序电压扰动的初相位。定子电压变换到频域的表达式为

本文采用等幅值Park 变换。当以PLL 输出角度θPLL进行变换时，Park 变换可分解为两部分，即

式中，Δθ 为由电压扰动产生的相角扰动。根据文献[13]可得其频域表达式为

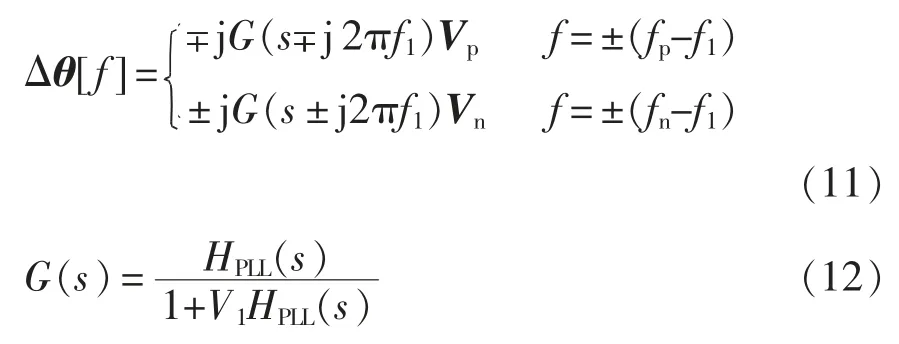
设转子侧基波频率为ωr1，由图3 可知，RSC 电流环Park 变换的变换角为

式（13）表明RSC 电流环Park 变换的变换角中引入了锁相环相角扰动，也因此引起转子电压响应和定子电压扰动之间的关联。

2.2.2 电流环建模

定子电压注入电压扰动，转子电流将产生相应的电流响应。RSC 电流环建模过程与并网逆变器相同，但需要特别注意转子侧与定子侧在频率上的差异。假设注入正、负序电压扰动后a 相转子电流的时域表达式为

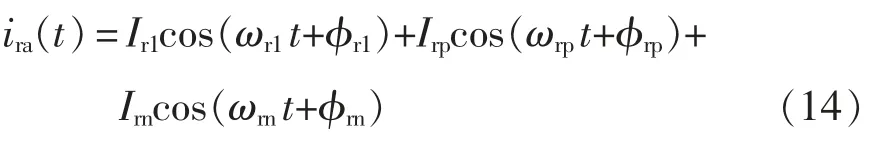
式中：Ir1、Irp和Irn分别为转子电流基波、正序电流响应和负序电流响应的幅值；ϕr1、ϕrp和ϕrn分别为转子电流基波、正序电流响应和负序电流响应的初相位；ωrp和ωrn分别为正序电流响应和负序电流响应的角频率，正序分量从定子侧变换到转子侧频率减小ωm，负序分量从定子侧变换到转子侧频率增加ωm。定转子角频率对应关系为

将式（14）变换到频域的表达式为

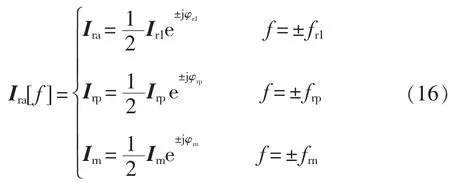
利用Park 变换将三相坐标系下的转子电流变换至dq 坐标系。考虑到变换引入的锁相环相角扰动，转子电流dq 分量的频域表达式分别为

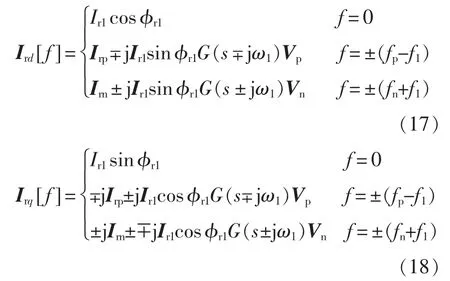
根据图3 所示控制结构，可得调制信号dq 分量的频域表达式为

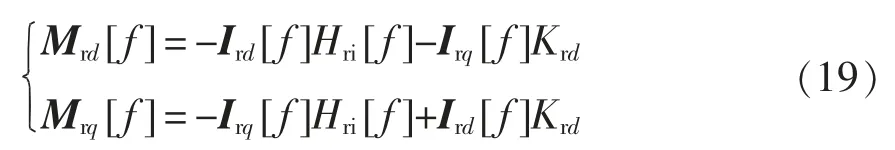
利用Park 反变换将dq 坐标系下的调制信号变换到三相坐标系，调制信号a 相的频域表达式为

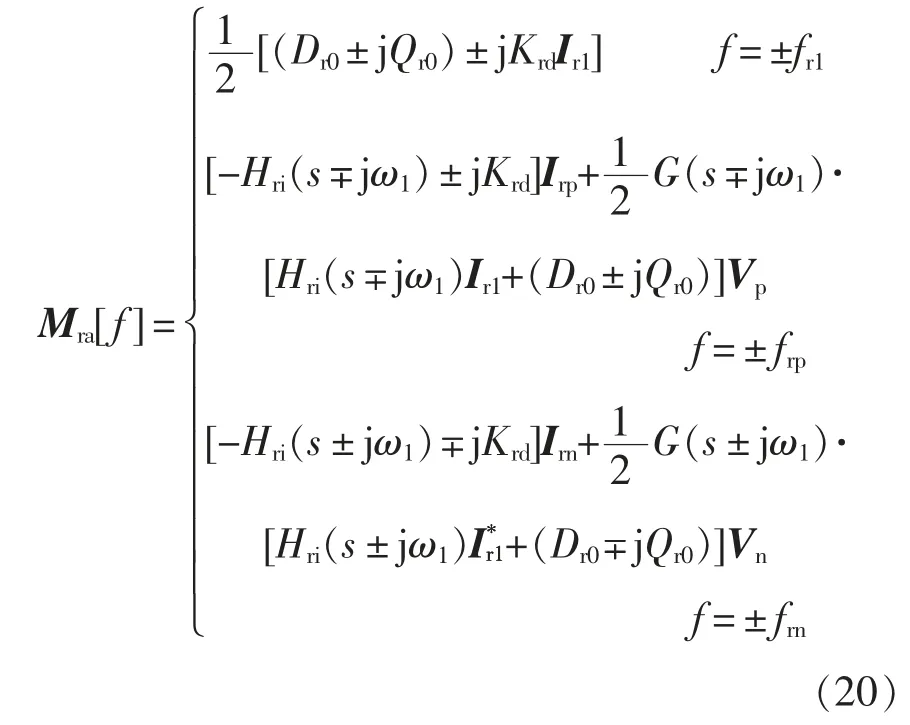
式中，Dr0和Qr0为电流环PI 环节输出的直流分量，可通过RSC 的稳态工作点求得，二者的关系为

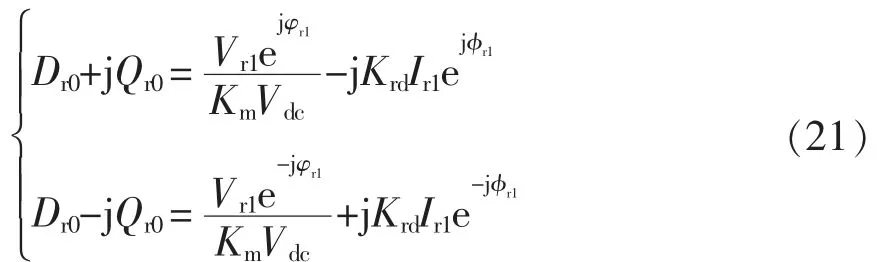
式中：Vr1和φr1分别为转子电压基波的幅值和初相位；Km和Vdc分别为调制系数和直流母线电压。

三相调制信号经过SPWM 产生三相转子电压，转子电压a 相的频域表达式为

2.3 序阻抗建模

将控制回路建模得到的转子电压响应表达式代入主电路建模得到的小信号电路方程，整理化简后可得RSC 的正、负序阻抗模型。为分析方便做如下定义

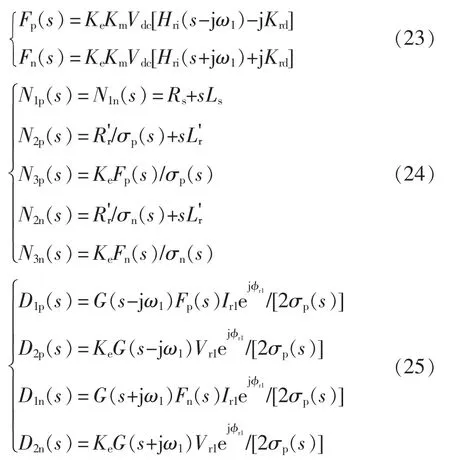
联立式（4）、式（6）和式（22）得到忽略励磁支路时RSC 的正、负序阻抗Z1p（s）和Z1n（s），即

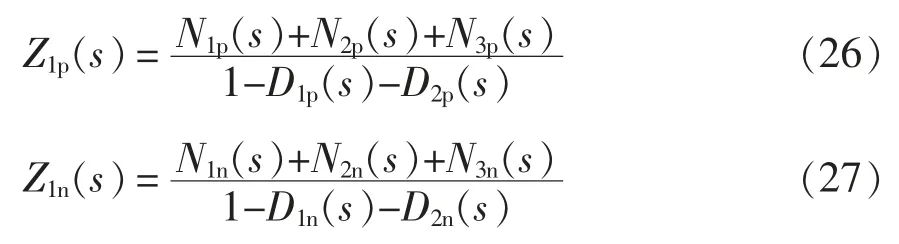
联立式（4）、式（7）和式（22）得到计及励磁支路时RSC 的正、负序阻抗Z2p（s）和Z2n（s），即

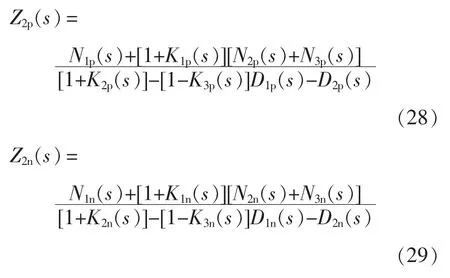
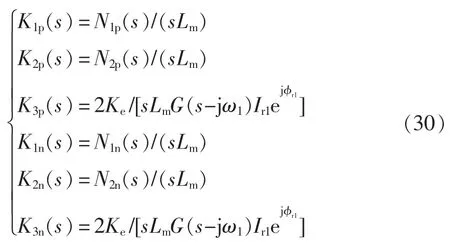
经过验证，式（28）和式（29）与文献[9]中通过电机的电压和磁链方程求得的RSC 正、负序阻抗相同，证明了本文建模方法的正确性。对比式（26）和式（28）及式（27）和式（29）可以看到，当计及励磁支路时，正、负序阻抗分子的第2 项、第3 项和分母的第1 项、第2 项的系数发生了变化。对于正序阻抗，这些系数的变化量为K1p（s）、K2p（s）和K3p（s）；对于负序阻抗，这些系数的变化量为K1n（s）、K2n（s）和K3n（s）。

K1p（s）和K1n（s）是定子阻抗和励磁支路阻抗的比值。K2p（s）和K2n（s）是经过绕组归算、频率归算的转子阻抗和励磁支路阻抗的比值。K3p（s）和K3n（s）与定转子匝比、励磁支路阻抗、锁相环传递函数以及运行工况有关。根据式（30）定性分析可知，励磁支路阻抗越大，稳态工作点越大，忽略励磁支路的影响越小。然而，为了确定简化建模方法能否适用一般情形，还需要详细分析这些项对正负序阻抗模型的影响。

此外，在定子注入频率为fp的正序电压扰动，定子电流还将产生频率为fp-2f1的负序响应；注入频率为fn的负序电压扰动，定子电流还将产生频率为fn+2f1的正序响应，即频率耦合现象。电压扰动和对应的耦合频率电流响应之比分别为正序耦合阻抗和负序耦合阻抗。同理可得忽略励磁支路时RSC正序耦合阻抗Z1pn（s）和负序耦合阻抗Z1np（s），即

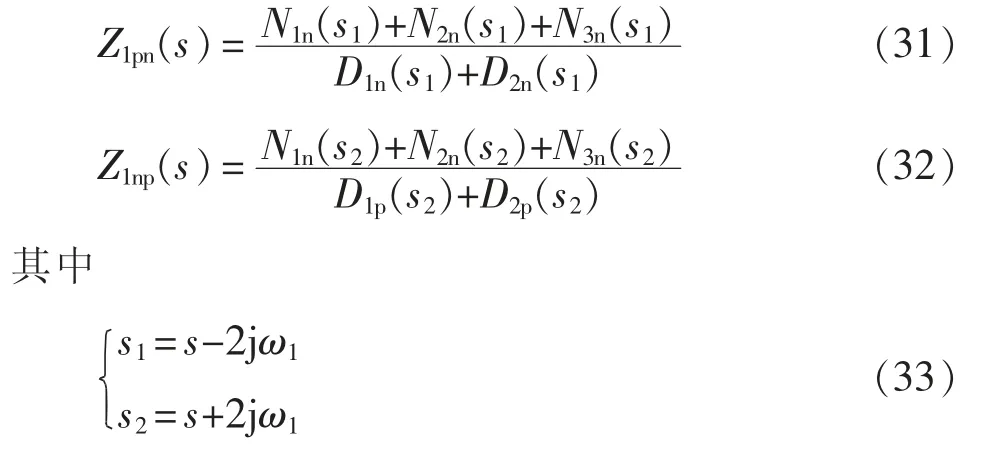
计及励磁支路时RSC 的正序耦合阻抗Z2pn（s）和负序耦合阻抗Z2np（s）分别为

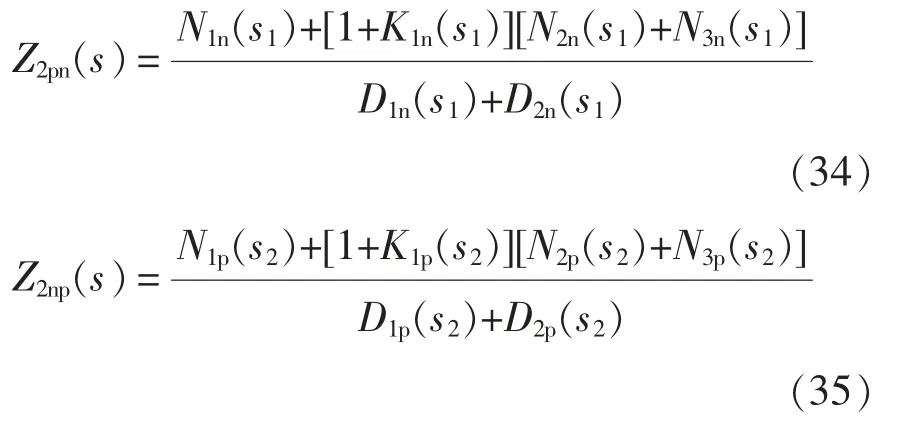
对比式（31）和式（34），式（32）和式（35）可以看到，当计及励磁支路时，正序耦合阻抗和负序耦合阻抗分子第2 项、第3 项的系数发生变化，变化量分别为K1n（s-j2ω1）和K1p（s+j2ω1），即K1p（s）和K1n（s）的频移。当励磁支路阻抗远大于定子阻抗时变化量很小，忽略励磁支路对频率耦合的影响也很小。

3 仿真分析

计及励磁支路的RSC 序阻抗模型如式（28）、式（29）、式（31）和式（32）所示，使用表1 所示的系统参数对理论模型进行仿真验证。

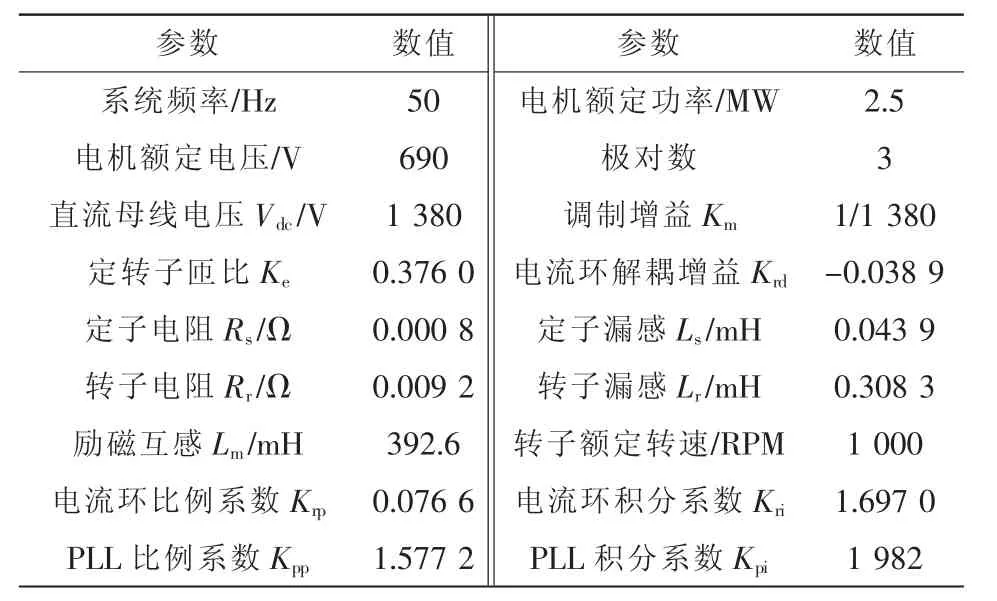
表1 系统参数Tab.1 System parameters

RSC 序阻抗验证结果如图6 所示。图中实线和虚线表示序阻抗的理论值，“*”和“o”分别表示相应序阻抗的仿真值。理论值和仿真值相吻合，验证了所建立阻抗模型的正确性。

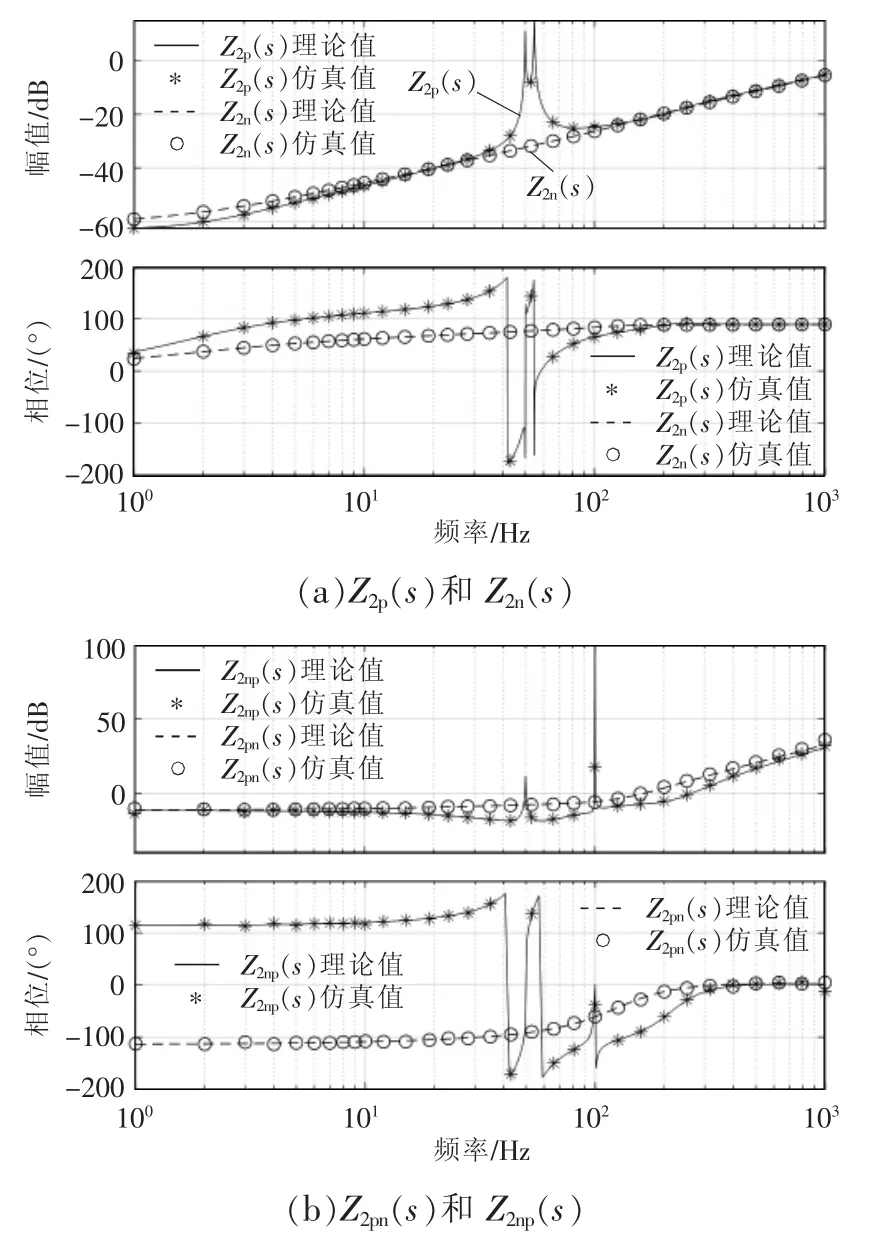
图6 RSC 序阻抗验证Fig.6 Verification of RSC sequence impedance

为了分析Z1p（s）和Z2p（s）的差异以及各种因素的影响。根据表1 参数，式（24）、式（25）和式（30）中与正序阻抗相关项的幅频响应特性曲线如图7 所示。

图7 正序阻抗相关项的幅频特性曲线Fig.7 Amplitude-frequency characteristic curves of terms related to positive-sequence impedance

对比图7（c）可知，在所研究频段K1p（s）的幅值远小于1；K2p（s）除了在电机转子机械频率处存在一个尖峰外，其他频率段的幅值也远小于1；K3p（s）在低频段幅值略大，与1 接近，但随着频率增加其幅值也远小于1。因此，根据式（26）和式（28），Z1p（s）和Z2p（s）的差异只可能出现在低频段和电机转子机械频率处。

根据图7（b）可知，在低频段D1p（s）的幅值远小于1，故K3p（s）在低频段的影响可忽略不计。根据图7 可知，在电机转子机械频率处，N2p（s）和N3p（s），D1p（s）和D2p（s）以及K2p（s）均存在尖峰，但是K2p（s）的幅值远小于其他项，故K2p（s）在电机转子机械频率处的影响也可忽略不计。以上分析表明，以表1参数所得的Z1p（s）与Z2p（s）之间相差很小。

对于一般情形，异步电机励磁支路的阻抗远大于定转子阻抗，故K1p（s）和K2p（s）的大小与之前的分析相同。在电机转子机械频率处，虽然K2p（s）存在尖峰，但D1p（s）和D2p（s）存在2 个符号相反的尖峰，故K2p（s）的影响可忽略不计。图8 表示不同参数K3p（s）的幅频特性曲线，实线表示不同转子电流，虚线表示不同PLL 带宽。图8 表明，当PLL带宽和转子电流较大时，K3p（s）在低频段已远小于1，此时不必考虑D1p（s）的影响；当PLL 带宽和转子电流较低时，K3p（s）在低频段较大，此时需要考虑D1p（s）的影响。

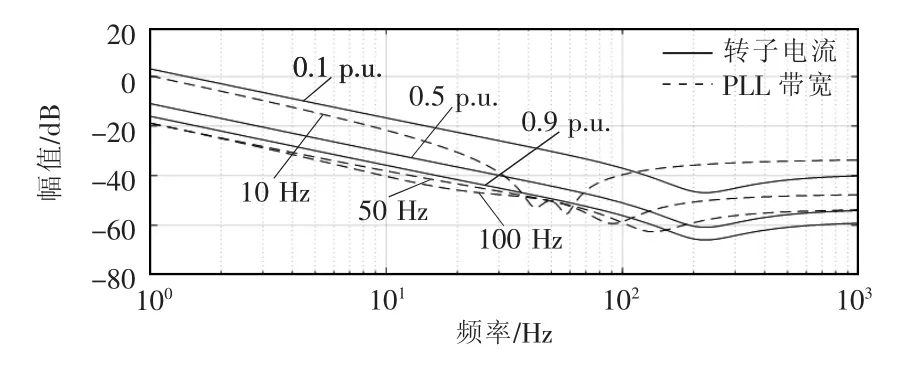
图8 不同参数K3p（s）的幅频特性曲线Fig.8 Amplitude-frequency characteristic curves of K3p（s）with different parameters

图9 给出了PLL 带宽为10 Hz、转子电流为0.1 p.u.时，不同电流环带宽D1p（s）的幅频特性曲线。由图9 可见，随着电流环带宽增大，D1p（s）的幅值也增大，此时K3p（s）的影响将不可忽略。然而，实际使用的电流环带宽不可能这么大，D1p（s）的幅值在低频段一直远小于1。因此，在不同PLL 带宽、电流环带宽和运行工况时K3p（s）的影响也可忽略不计。可知一般情形时Z1p（s）与Z2p（s）相差也很小。

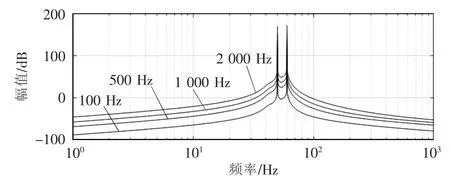
图9 不同参数D1p（s）的幅频特性曲线Fig.9 Amplitude-frequency characteristic curves of D1p（s）with different parameters

忽略励磁支路的简化模型和计及励磁支路的准确模型之间的差异如图10 所示。由图可见，2 种阻抗模型频率响应曲线之间的误差很小，表明了上述分析的正确性。因此，当励磁支路阻抗远大于定转子阻抗时，DFIG 的序阻抗建模可采用基于电机等效电路并忽略励磁支路的简化方法。

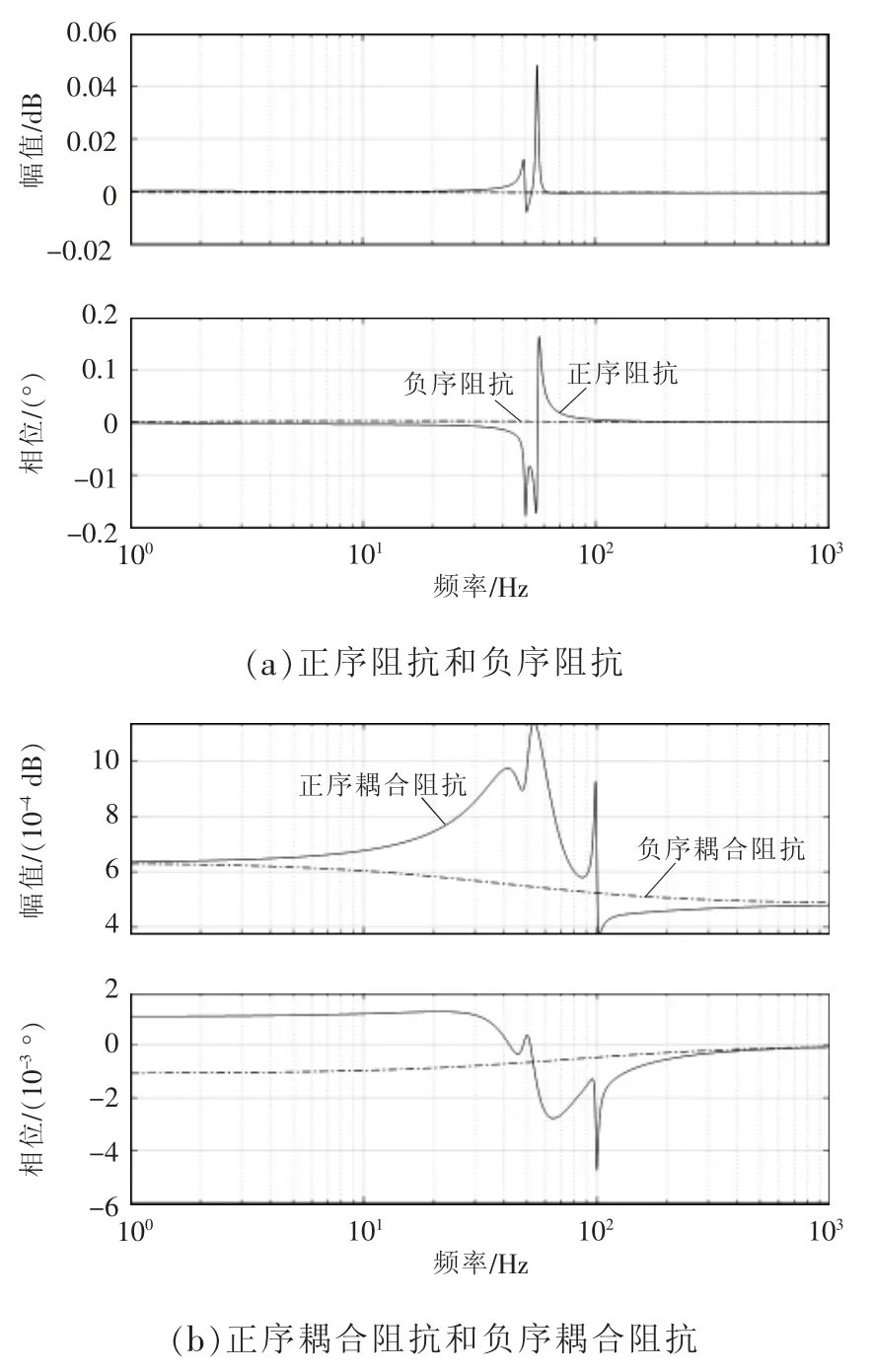
图10 简化模型和准确模型之间的差异Fig.10 Differences between simplified and accurate models

4 结语

本文研究了DFIG 序阻抗建模简化方法的使用条件，相较于电机的电压和磁链方程，采用等效电路建模更简单。根据电机的等效电路是否考虑励磁支路，建立了2 种RSC 正负序阻抗模型。通过扫频方法验证了所建立的阻抗模型的正确性。在此基础上，对比分析了不同情形下2 种阻抗模型之间的差异，结果表明当电机励磁支路阻抗远大于定转子阻抗时，即使不同的PLL 带宽、电流环带宽和运行工况条件，忽略电机励磁支路对RSC 序阻抗模型的影响极小，故DFIG 的序阻抗建模可采用此种简化方法。