重载轮胎面内柔性环振动建模与试验
刘志浩,刘钇汛,张 亚,高钦和,马 栋,黄 通
(火箭军工程大学 兵器科学与技术国家重点学科实验室,西安 710025)
重载轮胎作为军用车辆与地面直接接触的部件,除去空气阻力、坡度阻力和加速阻力等少数作用力,其他作用力都将通过轮胎作用在整车上,因此其力学特性直接影响车辆动力学特性。
GL073A ADAVANCE轮胎为重载子午胎,广泛应用于武器发射平台,其平均轴荷在10~13 t,为了保证其越野特性,重载轮胎具有较大的扁平率(胎侧径向长度和胎体宽度比值)[1],其胎侧径向长度与胎体宽度比值为0.93。重载轮胎具有气压高,阻尼低,花纹粗大,较大的扁平比的特点,因此在滚动过程中的噪声主要来源为面内结构振动噪声[2],且随着重载车辆速度提高至70 km/h,结构振动所形成的轮胎噪声达到65%。
路面激励经胎体和胎侧、空腔传至轮辋,造成了由于柔性结构振动所形成的低频振动[3]。因此开展基于轮胎结构模型的轮胎特性分析方法具有重要意义,而弹性基础环(ring on elastic foundation,REF)模型[4]作为轮胎振动解析模型的代表。
SWIFT模型作为刚性环模型的代表,将环当做刚性环进行研究,忽略了环内部的变形和振动,研究胎面和轮辋间的传递特性,在刚性环和轮辋中利用径向弹簧来表征轮胎的柔度,利用离散的胎面单元来分析接地特性;与之相对应的柔性环模型[5]则由可变性的圆环梁或壳组成,该模型可研究胎面的变形[6]及由于胎面变形所导致的轮胎高频特性[7],刚性环模型只可表征胎面与轮辋的错动阵型,因此其分析频段为70~80 Hz以下(一阶错动频率),刚性环模型为柔性环模型的“特例”,只是在利用柔性环模型进行计算时,只考虑错动阵型,而忽略高阶模态以及高阶模态所对应的胎面振动。同时柔性环模型可充分考虑轮胎的材料和几何非线性,且所用参数可以反应轮胎自身的特性而与工况无关,提高了轮胎建模的科学基础,同时也可省略刚性环模型中对路面的预处理[8],并且轮胎的振动特性均能求取解析解或者得到数值解,因此对于柔性环轮胎模型的研究就变得意义深远。
针对柔性环不同的建模方法,引申出了忽略弯曲效应只考虑拉伸作用的弦模型、考虑弯曲刚度的欧拉梁模型、考虑剪切作用的Timoshenko模型、正交各向异性板模型、环模型、壳模型和分布质量模型。
REF模型的另一个重要组成部分为弹性基础的建模,常用的假设为线性、均匀分布的弹簧,其力学特性包括只考虑径向刚度、考虑径向和切向刚度[9]和三维刚度特性(在径向和切向弹簧的基础上,添加了考虑轮胎面外特性的横向刚度),在刚度和质量非均匀分布的场合,比如行星齿轮的空间非均匀齿[10]和非均匀的轮胎[11],Wu等[12]研究了一般弹性基础的柔性环的自由振动,考虑刚度在空间圆周方向具有非均匀特性的情况,并求解出固有频率和阵型的解析解;Cooley等[13]研究了弹性基础刚度随负载和变形而变化所引起的柔性环动态特征的变化。
以上的文献对比中,均集中于分析胎体的动态特性及与轮辋的相互振动,在进行胎侧建模时,只是将胎侧等效为弹簧,承担传递力的特性,且针对轮胎动态分析试验模态分析方法也同样针对胎体的柔性及与刚性轮辋之间的相互运动,参照胎体与轮辋耦合模态测试的方法,对重载轮胎的模态特性进行分析,具体模态测试系统在模态测试部分详细叙述,将模态测试结果的模态置信判据(modal assurance criterion,MAC)列举如图1所示。
从图1可知,胎面与轮毂耦合所获取的模态参数,其中第1阶和第9阶,第2阶和第10阶,第3阶和第11阶,第4阶和第12阶,第5阶和第13阶,第6阶和第14阶,第7阶和第16阶,第8阶和第17阶均相互存在线性关系,MAC值为1,与模态向量正交相矛盾。

图1 重载轮胎胎体与轮辋耦合模态结果MAC值Fig.1 MAC value of the coupled modal between the tire tread and the rim
综上,基于传统的胎体与轮辋耦合试验模态与建模方法无法表征重载轮胎大于180 Hz的振动特性,因此不适用于扁平比接近于1的重载轮胎。因此本文针对重载轮胎扁平比接近于1的特点,提出建立基于弹性基础柔性环模型的重载轮胎面内振动模态模型,并开展胎体与胎侧耦合试验模态方法,重载轮胎面内振动模态模型包括含惯性力的弹性基础和柔性环,柔性环代表胎体,含集中质量的弹性基础代表胎侧。
本文的研究思路如图2所示。基于欧拉梁建模方法,对胎体的面内弯曲、拉伸变形进行分析,并将胎侧等效为离散质量块的惯性力和分段弹簧,建立轮辋自由状态下的胎体与胎侧的耦合动力学方程;采用逆向结构参数辨识法,即通过试验模态参数与模态参数解析解对比的方法,辨识轮胎的结构参数;利用辨识后的结构参数进行模态参数预测,并与试验模态结果进行对比。
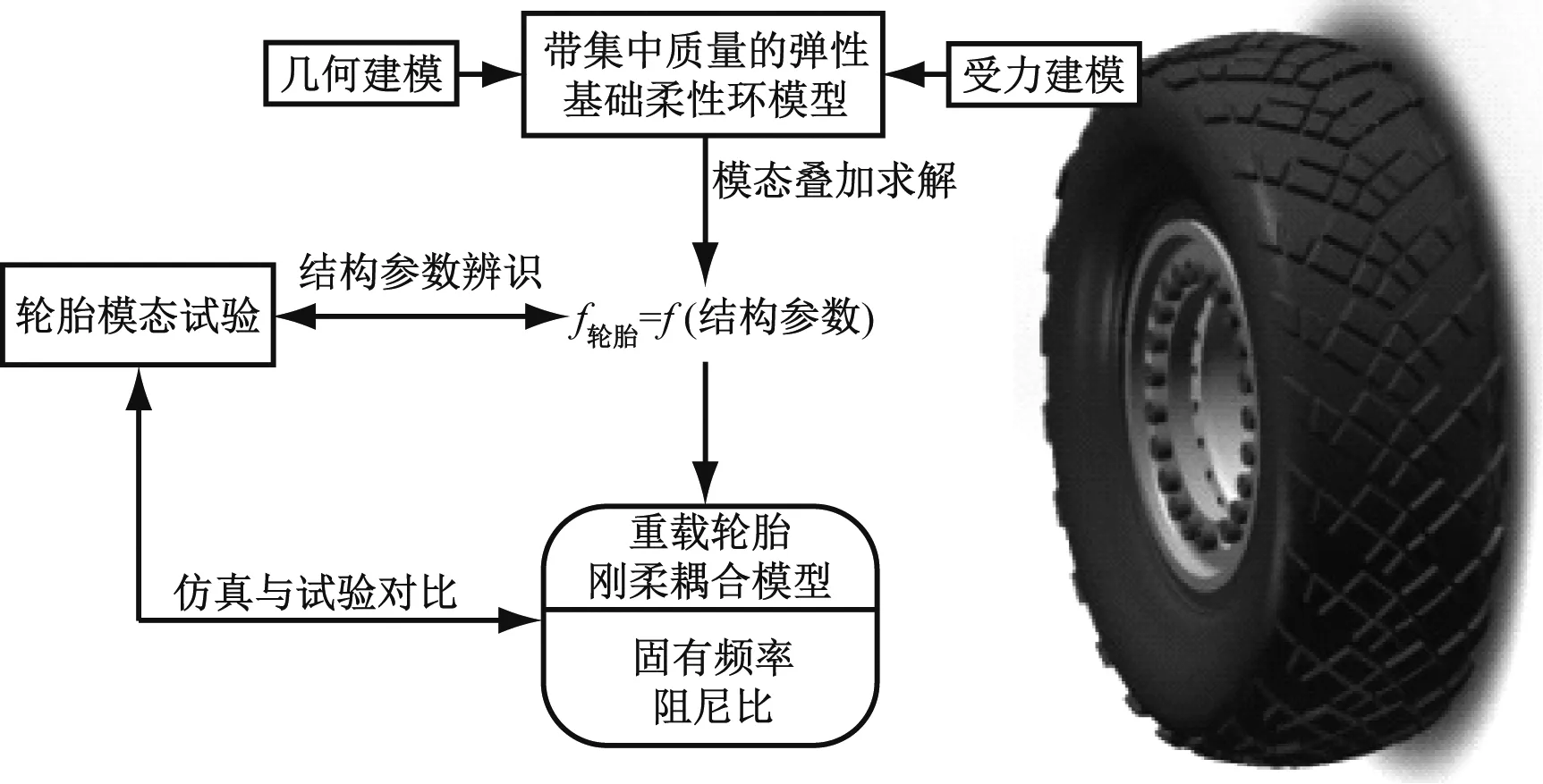
图2 文章研究路线图Fig.2 Research scheme of the paper
为表征重载轮胎与乘用车或卡车轮胎的区别,首先开展重载轮胎胎体与胎侧耦合试验模态研究,而后建立基于弹性基础柔性环的重载轮胎面内振动模态模型,并基于该模型开展结构参数辨识方法研究。
1 重载轮胎胎体与胎侧耦合试验模态研究
搭建重载轮胎胎体与胎侧的耦合模态测试系统,获得重载轮胎在标准充气压力、轮辋自由条件的重载轮胎胎体与胎侧耦合模态参数,并与传统的只测试胎体振动的模态试验进行对比,验证文中提出的基于胎体与胎侧耦合试验模态分析方法对于研究重载轮胎面内振动的有效性。
1.1 试验模态测试系统
搭建重载轮胎胎体与胎侧耦合模态测试系统[14],如图3所示。包括:轮胎固定支撑装置、力锤及电荷放大器、数据测试系统和PC计算机。
试验步骤为:
步骤1将PCB振动传感器分别粘贴于轮胎的胎体、胎侧和轮毂。
步骤2采用遍激励法,利用B &K力锤传感器和朗斯的电荷放大器,B &K力锤传感器将锤击力转化为电荷,后经电荷放大器,转化为DE-43数据采集器可识别的电压信号,沿胎体17个点进行径向激励。
步骤3对标准充气压力下的胎体径向激励-胎体径向响应、胎体径向激励-胎侧径向响应和胎体径向激励-轮毂径向响应的传递函数(见图3(b)和图3(c))。
步骤4利用最小二乘复指数法估计频率、阻尼和参与因子,求得的频率和阻尼。

(a)模态试验系统框图
1.2 重载轮胎胎体与胎侧耦合模态结果
试验模态频率和阻尼,如表1所示。阵型如图4所示。并求取各阶模态间的MAC值,如图5所示。

表1 胎体-胎侧-轮毂振动模态频率和阻尼Tab.1 Modal frequency and damping ratio of the coupled vibration between the tread,sidewall and rim

(a)错动阵型(第1阶与第9阶)
重载轮胎胎体与胎侧耦合试验模态结果(见表1、图4和图5)表明:

图5 胎体与胎侧耦合模态结果MAC值Fig.5 MAC value of the coupled modal between the tread and the sidewall
(1)胎体与胎侧耦合模态参数分析方法求取的模态参数与只分析胎体的模态参数分析对比,MAC值除个别点外,MAC值均小于0.2,各阶模态间相互正交,证明了基于胎体与胎侧耦合的模态参数测试分析方法的准确性。
(2)重载轮胎的阵型符合谐波特性,在0~180 Hz以内表现为胎体与胎侧的同向振动,即胎体与胎侧的阵型相位角差为0;在180~300 Hz内表现为胎体与胎侧的反向振动,胎体与胎侧的阵型相位角差为π/n,其中n为阵型的瓣数。从图4可知,与图3(b)中原点加速度振动传递函数中在180 Hz中存在幅值突变相一致。
分析其原因为:该特性由于其结构造成的,重载轮胎充气压力较大,承载较重,要求胎侧具有较厚的钢丝帘线层来防止重型承载的爆胎现象,胎侧与胎面的质量比增大,路面不平度作用于胎面时,在胎侧传递时,由于重载轮胎具有较大的扁平比,胎侧共振的波长较大,其发生共振的频率会降低,因此在重载轮胎模态测试与动力学建模中需将胎体与胎侧的耦合效应考虑在内。
2 重载轮胎弹性基础柔性环建模
重载轮胎结构三维坐标系OXYZ如图6所示。本文仅研究面内振动特性,只分析重载轮胎在OXY坐标系中的振动。

图6 重载轮胎三维坐标系Fig.6 Three dimensional coordinate of the heavy-loaded radial tire
根据对重载轮胎结构的物理特性的简化,本文将轮胎胎体-轮辋系统等效为由线性弹簧、胎侧分布质量、圆环梁和圆盘组成的系统,如图7所示。圆盘用来模拟轮辋,圆环用来模拟带束及与胎冠相连的胎体,线性弹簧和分布质量用来模拟胎侧的刚度和惯性,圆环梁和圆盘之间用径向和切向弹簧连接,径向弹簧分为径向上弹簧和径向下弹簧,如图8所示。其中径向上弹簧连接胎侧质量和轮辋,径向下弹簧连接胎体与胎侧质量块,刚度分别为ksr1和ksr2,以此类推切向弹簧分为切向上弹簧和切向下弹簧,其中切向上弹簧连接胎侧质量和轮辋,切向下弹簧连接胎体与胎侧质量块,刚度分别为ksθ1和ksθ2。
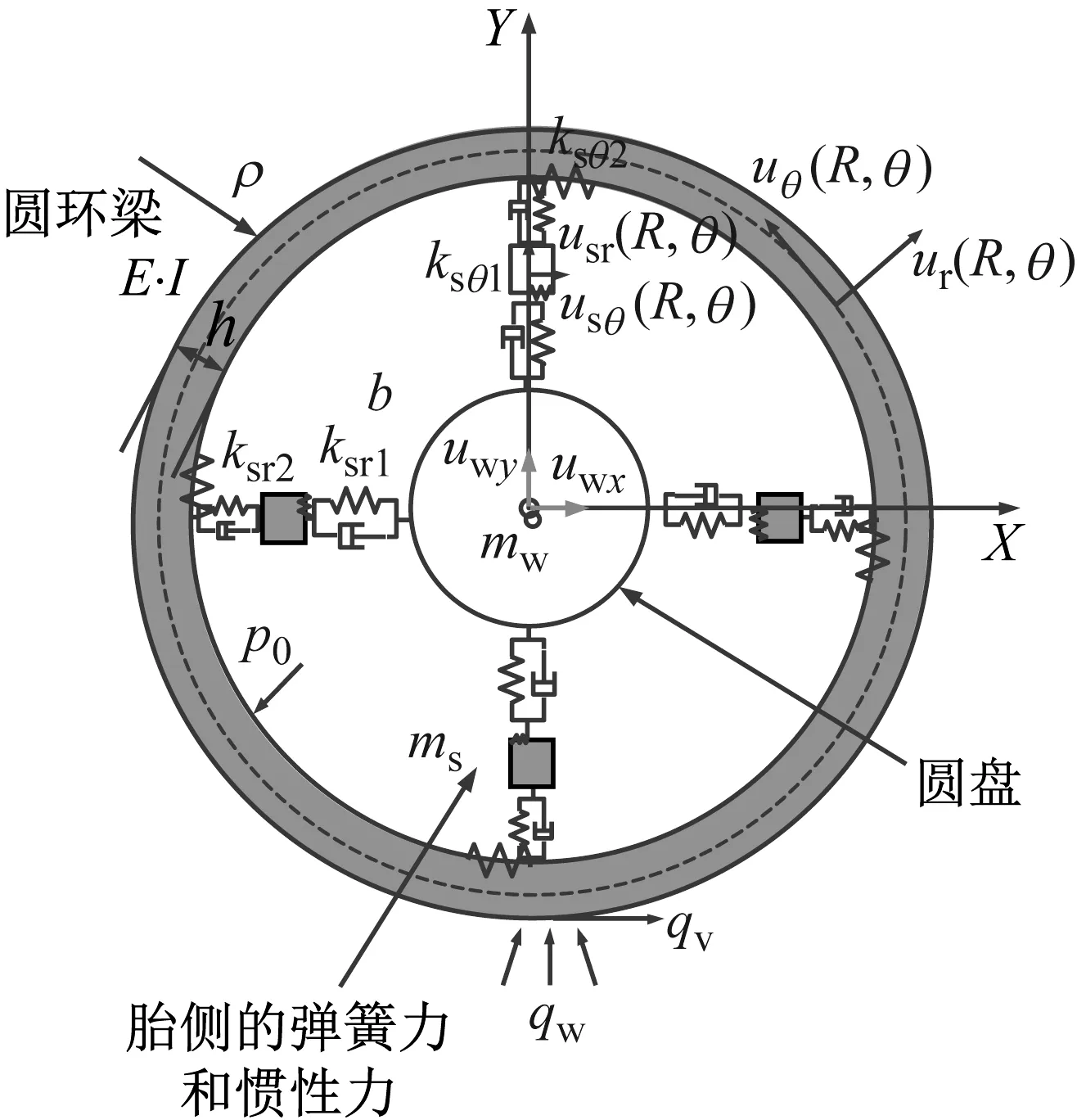
图7 基于弹性基础柔性环的重载轮胎面内模型Fig.7 In-plane tire ring model with the elastic foundation of the heavy-loaded radial tire
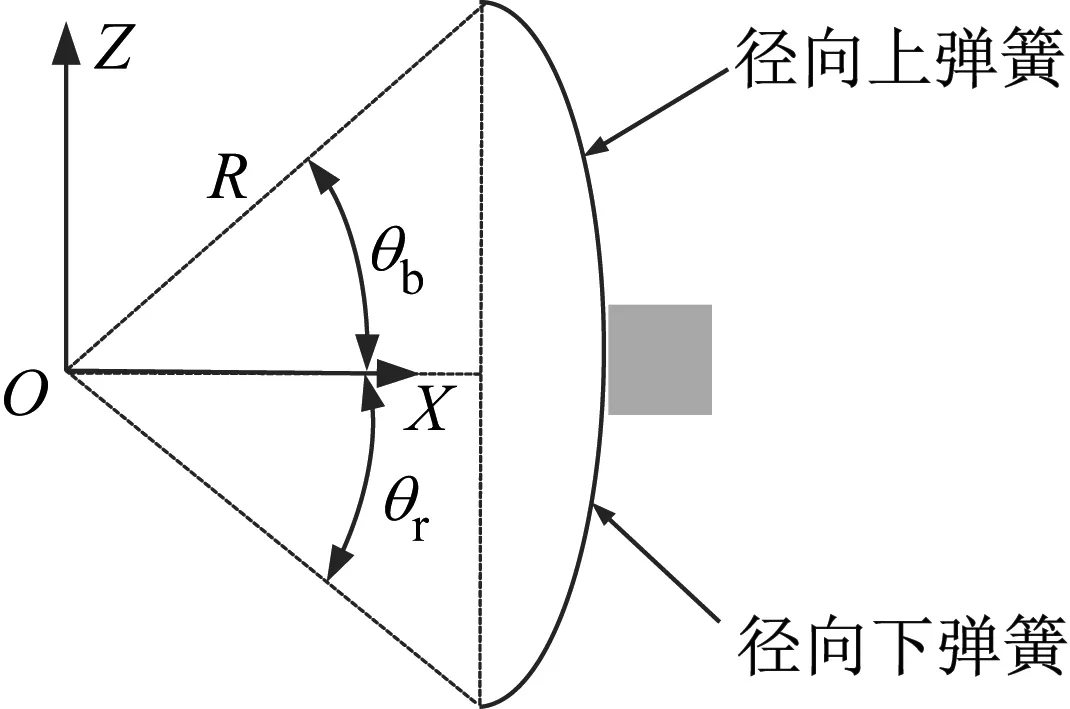
图8 胎侧径向弹簧Fig.8 Radial spring of the tire sidewall
假设:① 轮胎断面在变形后仍保持平面特性并垂直于轮胎中截面;② 轮胎在变形过程中温度和气压保持不变;③ 不考虑轮胎平面外特性。
定义两个坐标系:XOY和X1O1Y1,XOY为以初始位置轮辋中心O为原点的绝对坐标系,n1,n2分别为X轴、Y轴单位向量;坐标(x,y)和坐标(x*,y*)分别为固定坐标系XOY和旋转旋转坐标系X1O1Y1,(r,θ)(r,φ)分别为在旋转坐标系和固定坐标系中点的极坐标。胎体固定和旋转坐标系如图9所示。

图9 胎体固定和旋转坐标系Fig.9 Fixed and rotational coordinate
P为圆环上任意一点,与X轴的夹角为φ,与X1轴的夹角为θ,圆环的旋转角速度为Ω,uθ、ur分别为P点在坐标系X1O1Y1中的切向和径向变形。两个坐标系的转换关系为
φ=θ+Ωt
(1)
则,坐标(x,y)和坐标(x*,y*)的转换关系为
(2)
2.1 系统能量分析
计算得到系统在运动过程中的动能和势能的表达式。
2.1.1 系统动能
圆环动能T1,轮辋动能T2,胎侧分布质量动能T3,分别表示为
(3)
(4)
(5)
式中,mw,Iw,γ分别为圆盘的质量、转动惯量及转角。
则系统总动能可表示为
T=T1+T2+T3
(6)
2.1.2 系统势能
结构势能表示为
(7)
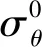
以一半胎体圆环为研究对象,根据在Y方向力的平衡,如图10所示。可得
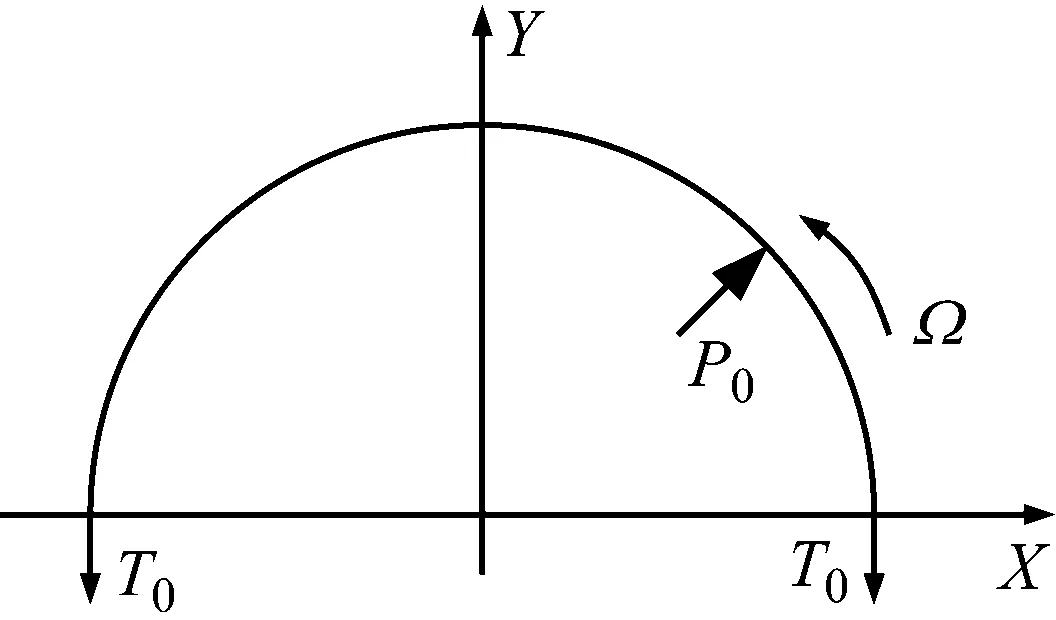
图10 胎体初始应力Fig.10 The pre-tension of the tread
(8)
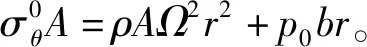
胎侧径向和切向弹簧的弹性势能
(9)
式中,U2为胎侧弹性势能。
则系统总势能可表示为
U=U1+U2
(10)
2.2 外力做功分析
外力做功包括轮胎充气压力做功W1,切向力做功W2,径向力做功W3,轮辋作用力Fwx做功W4,轮辋作用力Fwy做功W5,W6为轮辋作用力矩Tw做功。表示为
W=W1+W2+W3+W4+W5+W6
(11)
气压做功可以表示成气压和变形体积的乘积,对于横向一致的梁模型,此可以表示成梁中性面变形面积和梁宽度以及气压的乘积,中性面变形面积计算为
(12)
整理得
(13)
则,充气压力做功表示为
(14)


(15)
W2~W6分别表示为

(16)

(17)
W4=Fwxx
(18)
W5=Fwyy
(19)
(20)
2.3 哈密尔顿变分原理
采用哈密尔顿能量变分原理建立重载轮胎运动方程
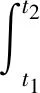
(21)
式中的能量项如式(3)~式(20)表示。
以ur,uθ,usr,usθ,x*,y*和γ为独立变量,利用变分原理,建立重载轮胎面内振动方程,如式(22)~式(28)所示。
(22)
(23)
x*cosθ)-ksr2(ur-usr)=0
(24)
x*sinθ-γr)-ksθ2(uθ-usθ)=0
(25)

(26)

(27)
(28)
式中:式(22)为胎体沿径向方向的振动;式(23)为胎体沿切向方向的振动;式(24)为胎侧沿径向方向的振动;式(25)为胎侧沿切向方向的振动;式(26)为轮辋沿水平方向的振动;式(27)为轮辋沿垂直方向的振动;式(28)为轮辋的转动方程。
3 重载轮胎胎体与胎侧耦合模态解析解
3.1 方程简化分析
子午胎胎体由钢丝、橡胶等复合材料组成,且钢丝沿轮胎的子午线方向,其周向拉伸刚度较大,且在400 Hz频率内,GL073子午胎的模态振型均为胎体面内弯曲振型,而与胎体拉伸刚度相关的呼吸振型未出现在该频率范围内,验证了“胎体不可伸长假设”的有效性。
胎体、胎侧不可伸长假设,轮辋固定支撑,非旋转,则
(29)
则重载轮胎胎面-胎侧-轮毂耦合动力方程转化为
(30)
(31)
在研究轮胎的2阶以上模态时,由于模态阵型的对称性,轮毂的约束不会影响胎面与胎侧的耦合振动,即轮辋固定支撑条件下的两瓣以上(包括两瓣)所对应的固有频率与轮辋自由状态下的相同阵型所对应的固有频率相同,轮辋的约束条件仅影响重载轮胎的错动阵型。
3.2 重载轮胎胎体、胎侧不可伸长,轮辋固定支撑模态解析解
利用模态叠加原理,进行方程求解,推导出轮胎各阶固有频率与轮胎结构参数间的关系。
胎面-胎侧-轮毂耦合动力学模型为偏微分方程组,利用模态叠加法,将偏微分方程组转化为空间和时间的常微分方程进行求解。
(32)
则胎面与胎侧的耦合方程为
(33)
则方程转化为
ρAms(1+n2)2ω4-[ρA(1+n2)K22+
ms(1+n2)K11]ω2+K11K22-K12K21=0
(34)
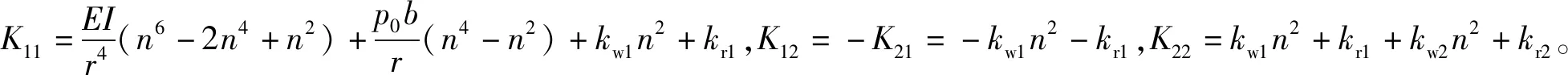
求解得
(35)
则胎体与胎侧阵型同向所对应的固有频率为
(36)
则胎体与胎侧阵型反向所对应的固有频率为
(37)
4 结构参数辨识及模态预测
重载轮胎的模态参数解析解中的参数包括几何参数和物理参数两部分,如表2和表3所示。

表2 GL073A型重载轮胎几何与结构参数Tab.2 The geometrical and structural parameters of GL073A tire

表3 待辨识的重载轮胎柔性梁参数Tab.3 The identified parameters of the flexible beam tire model
4.1 结构参数辨识
利用轮胎标准气压下的模态参数,利用遗传算法[15]对轮胎动力学方程中的结构参数进行辨识。其优化流程,如图11所示。
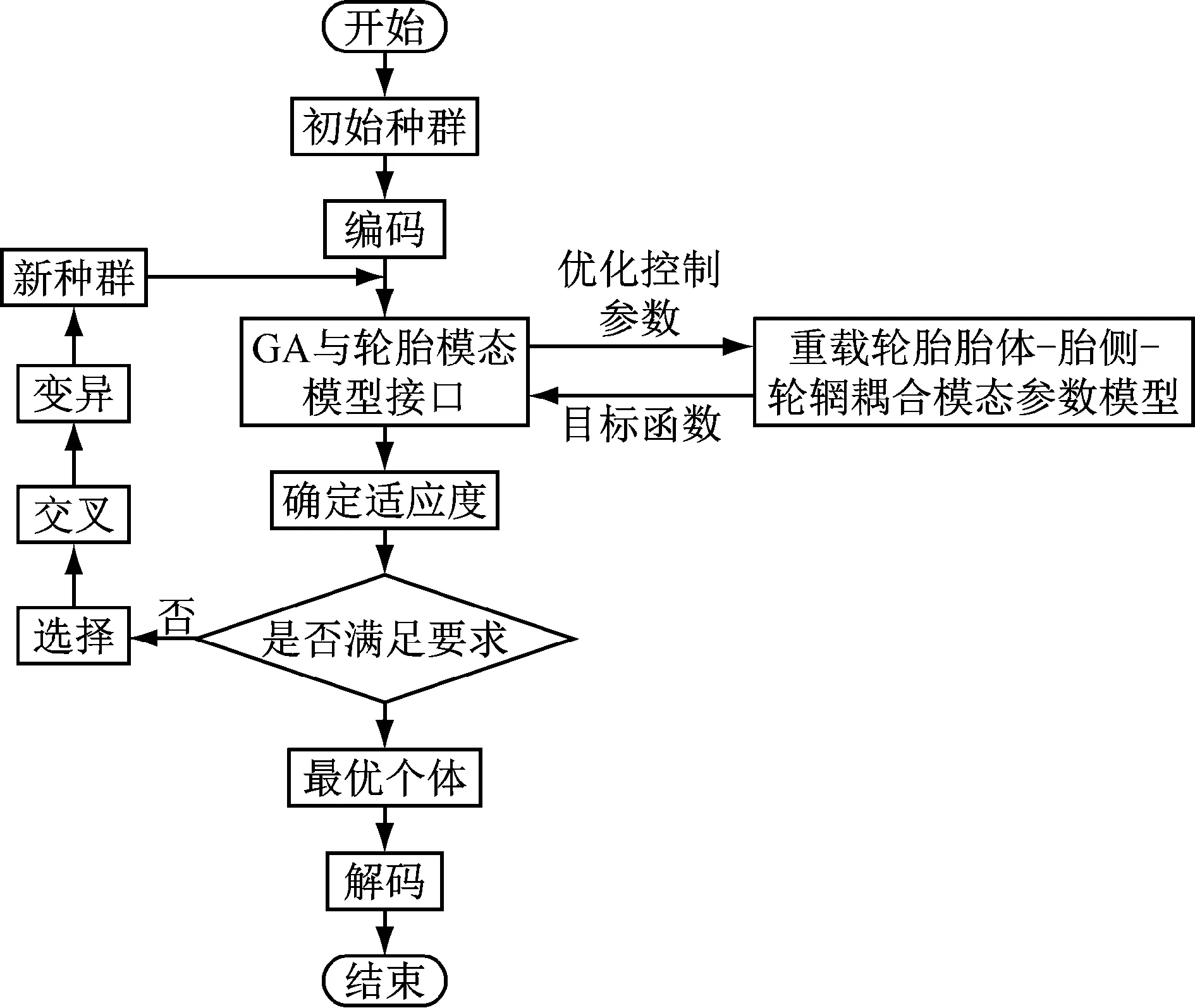
图11 遗传算法轮胎结构参数寻优流程图Fig.11 The scheme of the parameter identification utilizing GA
编码操作把需要解决的问题从解的空间转化到便于搜索的求解空间,而解码操作则与编码过程相反,由解的空间转换为问题空间。遗传算法的确立分为:基本参数的确定、变量范围的确立、选择算子和系数的确立、目标函数的确定,如表4所示。

表4 遗传算法结构参数Tab.4 Parameters of the GA
其中,选择过程就是通过选择群体中生命力较强的个体来产生新的群体,而选择的过程,则是通过选择算子完成个体间优胜劣汰的操作的。本文采用轮盘赌选择算子,即个体可被选择的概率等于其适应度值在群体中各个个体适应度之和中占的比重,其中适应度值越高,被选中的概率就越大,进行遗传操作的可能性就越大。对选择的两个个体采用单点交叉的方法进行重组,从而产生两个新的个体。
(38)
选取重载轮胎胎体与胎侧3~6瓣阵型的同向和反向的模态频率,利用式(36)~式(37),以误差的均方值优化目标函数,如式(39)所示。
(39)
遗传算法优化过程如图12所示,结果如表5所示。

图12 遗传算法优化过程Fig.12 The optimizing process utilizing GA

表5 辨识的重载轮胎结构参数Tab.5 Identified structural parameters N/m
轮胎结构参数随迭代过程的变化曲线,如图13所示。其中图13(a)~图13(e)分别为弯曲刚度E·I、径向上弹簧刚度ksr1、径向下弹簧刚度ksr2、切向上弹簧刚度ksθ1和切向下弹簧刚度ksθ2的优化值。

(a)弯曲刚度优化值
优化结果表明:从图12和图13可知,随着迭代次数的增多,目标函数值趋向于最低,同时各待辨识的结构参数趋向于稳定值,均收敛于辨识的轮胎结构参数。
4.2 模态预测
利用寻优后的轮胎结构参数,对轮胎的固有频率进行对比分析,如表6所示。

表6 试验与解析模态频率对比结果Tab.6 Compared results between the experimental and analytical modal frequency
从表6可知,① 考虑胎体与胎侧耦合弹性基础的柔性环模型理论模态预测值和实测值的误差小于3%,说明了考虑胎体与胎侧耦合的弹性基础的柔性环模型对于分析重载轮胎在0~300 Hz内的胎体-胎侧-轮辋耦合模态的可靠性;② 重载轮胎的胎体与胎侧的振动特性在第7阶和第8阶约160 Hz,存在 “跳变”特性,分析原因为重载轮胎的振动特性由胎体与胎侧同向振动转变为反向振动;③ 重载轮胎的胎体与胎侧的反向振动随着模态阶数的升高成指数增长;④ 重载轮胎的高频振动形式主要变现为胎体与胎侧的反向振动。
5 结 论
本文针对扁平比接近1的重载轮胎,提出一种面内振动模态测试与动力学建模方法,包括:① 提出考虑胎体-胎侧-轮毂耦合作用面内振动模态测试与分析方法;② 提出针对重载轮胎面内胎体-胎侧-轮辋耦合作用的弹性基础柔性梁动力学建模与参数辨识方法。通过理论建模、模态求解和试验模态分析。得到以下结论:
(1)基于胎体-胎侧-轮辋耦合作用的试验模态分析结果表明,重载轮胎的阵型符合谐波特性,在0~160 Hz内表现为胎体与胎侧的同向振动,在160~300 Hz内表现为胎体与胎侧的反向振动,该模态试验首次揭示了重载轮胎的胎体与胎侧的耦合特征,为理论分析奠定了试验基础。
(2)基于弹性基础的柔性梁模型建立了重载轮胎的胎体-胎侧-轮辋耦合动力学模型,首次建立了轮胎几何、物理参数和胎体-胎侧-轮辋耦合模态的解析表达式,为重载轮胎的结构分析提供了理论指导。
(3)基于重载轮胎的试验模态参数,利用遗传算法辨识重载轮胎的结构参数,并将试验模态结果与胎体-胎侧-轮辋耦合模态的解析解进行对比分析,预测误差小于3%,同时模态的解析解可以预测试验无法测得的高频模态。
(4)通过模态解析解的分析,重载轮胎的胎体与胎侧的同向振动随着模态阶数的升高,收敛于特定值,而反向振动随着模态阶数的升高成指数增长,因此重载轮胎的高频振动形式主要变现为胎体与胎侧的反向振动。
重载轮胎面内的胎体-胎侧-轮辋耦合模态测试和动力学建模方法表征了重载轮胎的同向与反向振动特性,可将分析频率由0~160 Hz,扩展到0~300 Hz,提供了重载轮胎高频振动分析的一种可行性方法。

