船舶尾部避振穴的设计研究
叶星宏,夏利娟
(1.上海交通大学 海洋工程国家重点实验室,上海 200240;2.高新船舶与深海开发装备协同创新中心,上海 200240)
为了减小船舶的振动、提高船舶的舒适性和宜居性,空气弹簧结构在船舶工程中的应用愈发普遍。空气弹簧是一种利用囊内空气在压缩、膨胀过程中产生的回复力来实现隔振和缓冲的装置,具有固有频率低、承载能力强、刚度可调等优点[1-2],目前常用作船舶主辅机的隔振基座。陈志敏等[3]利用ADAMS机械动力学分析软件,在充分考虑空气弹簧非线性特点的条件下,准确模拟了空气弹簧对某潜艇推进主机的隔振效果,为隔振系统的选型和布置提供了参考;Li等[4]设计了由磁悬浮驱动器和空气弹簧构成的主被动隔振系统,结合了空气弹簧的大承载能力和中高频段良好的隔振性能、以及磁悬浮驱动装置功率消耗低和有效消去低频正弦波的特性,并在200 kW柴油机试验中得到了验证。类似的空气弹簧结构在船舶动力机械隔振方面已有许多应用实例[5-7],对于减小主辅机等往复式机器的激励作用具有良好的实用效果。
另一方面,螺旋桨激振是船上出现有害振动的又一重要原因。避振穴是船舶尾部用于减小螺旋桨激励向船体传递的结构,由表面橡胶板、四周钢板以及内封气体构成,其隔振原理与空气弹簧有许多相似之处。避振穴一般设置在螺旋桨上方约d×d的区域(d为螺旋桨直径),中心点位于桨盘前0.1d处,对该区域船体外板及内部结构进行挖孔,代以橡胶板覆盖于外壳表面,并对内部封闭腔室进行充气,构成类似于空气弹簧的密闭充气腔体结构,如图1所示[8]。国内避振穴的工程应用实例最早可追溯到1955年的内河测量艇[9]。到20世纪90年代,马佐璋等[10-12]针对避振穴的固有频率、减振性能和阻力性能开展了一系列试验研究,认为避振穴在具有显著减振效果的同时,对船速不会产生明显影响,并提出了避振穴设计过程中对橡胶板变形、气密性、耐腐蚀性等的要求。近年来,Lee等[13-15]通过理论分析和实船测试等一系列研究,提出了在不改变船体结构布置的前提下,在船体尾部外壳表面加装充气橡胶薄膜装置的方法,利用相消干涉的原理减小螺旋桨对船体的激振,取得了较好的效果。

图1 避振穴示意图Fig.1 Sketch of anti-vibration cave
然而,此前对避振穴的研究大多采用模型试验和实船试验,对于避振穴自身振动特性以及内在的隔振机理缺乏深入的分析,往往需要依靠经验和反复试算进行设计。本文通过理论分析,推导得到避振穴固有频率的近似计算方法,结合简化的两自由度(degree-of-freedoms,DOFs)隔振系统,研究避振穴在不同条件下的隔振性能,并在实船设计中加以验证,以求为避振穴设计提供有用的参考。
1 避振穴固有频率理论计算
1.1 避振穴固有频率计算模型
建立避振穴的固有频率计算模型,如图2所示。在实际设计中,避振穴的底板一般近似为正方形,记其边长为L,由密度为ρ、厚度为h的橡胶制成;橡胶板与四边简支固定,为防止变形过大还会施加有初始预张力fx、fy;避振穴四周及顶板由钢板构成,高度为H;避振穴腔内充有绝对压强为p=p0+Δp的空气,其中:p0为外界气压;Δp为腔内气体净压强。由于橡胶板固有频率显著低于周围钢板,接近螺旋桨的激励频率,同时处于螺旋桨脉动压力的主要作用区域,是避振穴设计的关键。以基频振动(一般对应(1,1)模态)为例,推导橡胶板固有频率的近似计算公式,对于其余高阶模态可类似地进行求解。

图2 避振穴固有频率计算模型Fig.2 Calculation model of natural frequency of anti-vibration cave
1.2 避振穴固有频率推导过程
对于受初始预张力的四边简支方形板,其自由振动方程为
(1)
式中,D为板的抗弯刚度。求解该方程,可得一阶固有频率表达式为
(2)
橡胶板在腔内气体压强作用下,将发生大挠度弯曲变形,产生附加的薄膜力,提高板的等效刚度。采用板壳理论中的能量法计算橡胶板的大挠度弯曲。板的总势能Π可写为
(3)
式中:Um为无预张力条件下薄板应力状态对应的变形能;Uf为预张力产生的变形能;Ub为板的弯曲变形能。
在进行板的大挠度弯曲计算时,采用冯·卡门板壳理论[16]描述位移和应变之间的非线性关系
(4)
将式(4)代入式(3),并对z进行积分,可得Um、Uf、Ub三者的表达式分别为
(5)
根据边界条件的对称性,可设板的变形函数为
(6)

(7)
式中,
(8)

(9)
结合胡克定律,可得板的大挠度弯曲在四边产生的平均中面应力为
(10)
考虑腔内气体回复力的作用。腔内气体的体积V与绝对压强p满足关系式
p·Vm=const
(11)
式中,m为气体的热力学指数。将式(11)对位移s进行求导,可得
(12)
由于p=p0+Δp,而外界气压p0为一常数值,故有
(13)
式中,负号为压力的变化趋势与容积的变化趋势相反,在计算刚度时应取其绝对值。

(14)
(15)
由此,基于受初始预张力的四边简支板固有频率表达式,综合考虑板的大挠度弯曲和空气弹簧的作用后,可得避振穴橡胶板一阶固有频率的近似计算式为
(16)
式(16)计算得到的是橡胶板干模态基频,对于实际应用中避振穴橡胶板单面触水的情况,可参考金咸定等的研究中接水船板振动的经验计算公式,取单位面积的附连水质量为ερfb,其中:系数ε通过对比有限元计算结果进行修正,对于本文计算的方形板取为0.25;ρf为流体密度;b为板的短边长,此处即为L。由此,在考虑附连水质量后,式(16)分母变为(ρh+ερfL)×L4,分子保持不变。
1.3 避振穴固有频率计算结果验证分析
Amabili等[18]基于Mooney-Rivlin本构模型,对一面受初始预张力的方形橡胶板进行了模态试验和计算,之后分析了该板在气体静压力作用下的大挠度变形。试验模型的相关参数汇总,如表1所示。
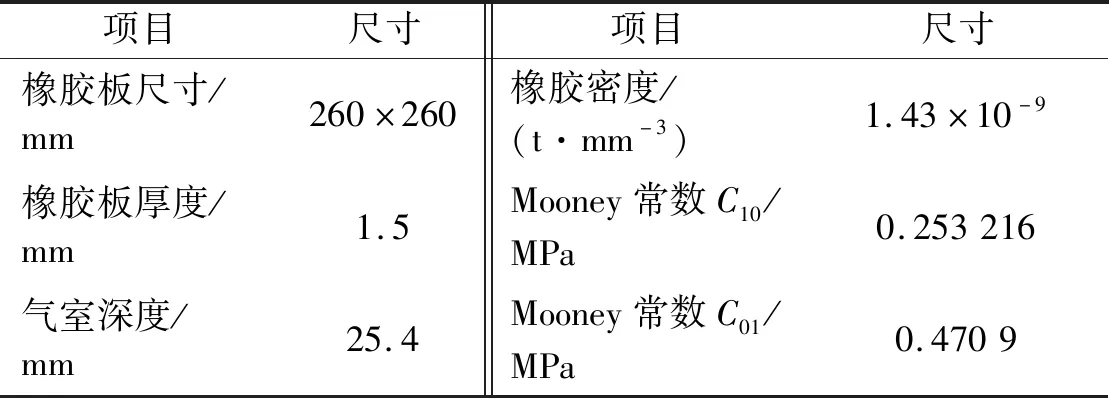
表1 Amabili等的研究中试验模型的相关参数Tab.1 Parameters of test model in studies on Amabili et al
本文采用1.2节的计算方法,对该文献所述的橡胶板模态和挠度进行分析,同时在ABAQUS软件中建立尺寸以及材料与之一致的有限元模型进行对比验证,如图3所示。各钢板及橡胶底板采用S4R壳单元进行模拟,网格尺寸约为5 mm,并在橡胶底板四边施加简支约束;腔内气体通过在inp文件中加入*fluid cavity命令,并定义腔体内表面及参考节点,由ABAQUS自动生成F3D4单元进行填充模拟。

图3 根据Amabili等的研究建立的有限元模型Fig.3 Finite element model based on studies on Amabili et al
Amabili等在进行模态分析时,橡胶板仅受四边初始预张力作用,并未构成充气密闭气室的一部分,故使用式(16)进行理论计算时,只需考虑板自身属性及初始预张力两项的作用。橡胶板基频计算结果汇总,如表2所示。各结果相互间误差均在3%以内,本文计算结果与文献结果吻合良好。

表2 橡胶板基频Tab.2 Fundamental frequency of rubber plate Hz
Amabili等在进行橡胶板大挠度弯曲分析时,气室内的净压强以1 379 Pa为步长逐步由0增压至17 927 Pa。本文采用式(7)进行板的大挠度理论计算,同时使用非线性有限元进行求解,得到结果汇总如图4所示。可见,各曲线均反映了随着充气气压的增大,橡胶板中心点挠度也在逐步增大,且增大的速度逐渐放缓。采用能量法进行理论计算时,仅取变形函数的第一项得到的挠度在载荷较低的时候偏大,在载荷较高的时候偏小,但总体上吻合较好,能较为准确地模拟橡胶板在均匀外载荷作用下的变形。
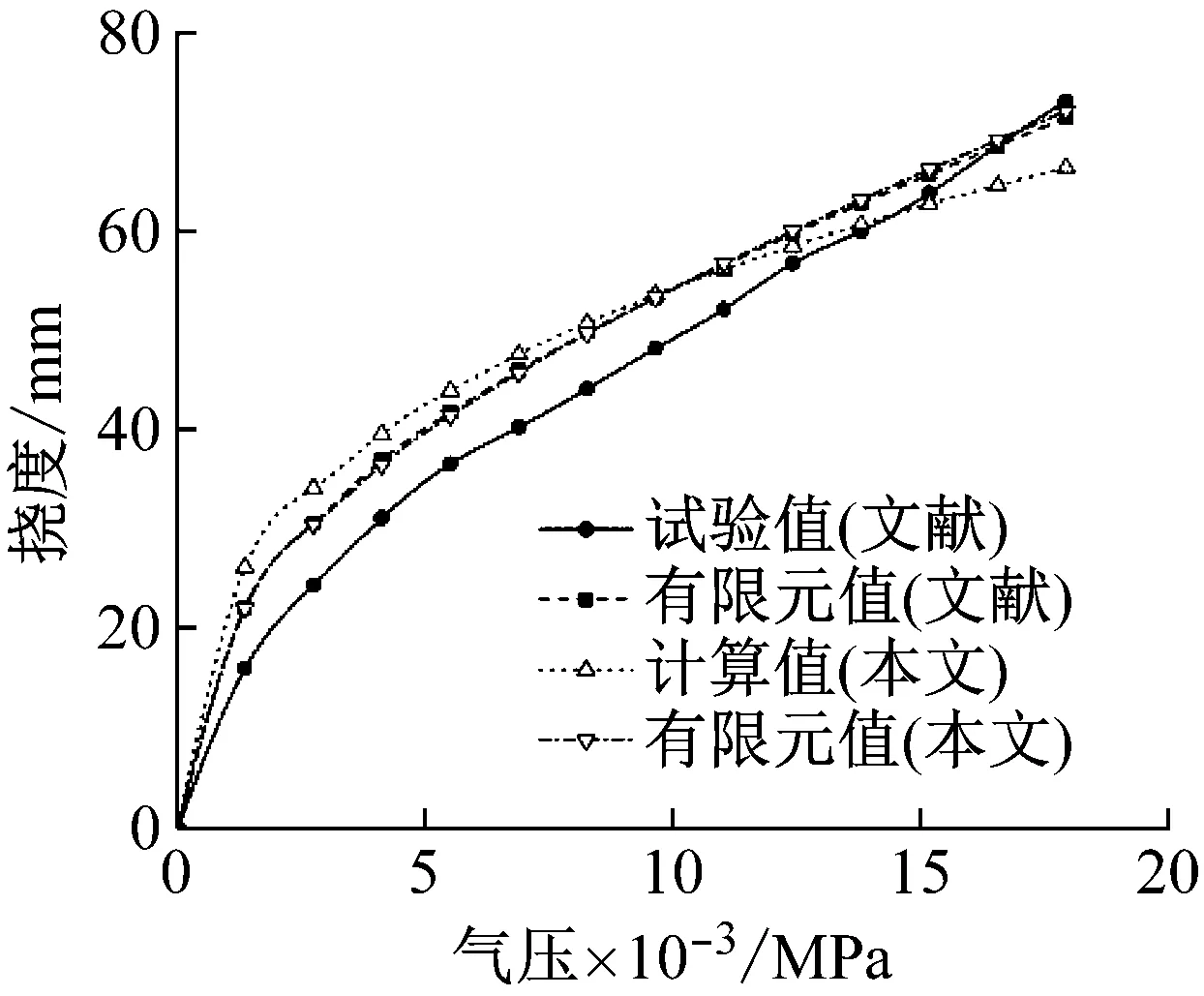
图4 橡胶板中心点的挠度-气压曲线Fig.4 Deflection-pressure curve of rubber plate center point
1.4 避振穴设计参数对固有频率的影响分析
采用理论计算和有限元计算,分析橡胶板板厚h、初始预张力fx和fy、腔内气体净压强Δp等关键设计参数对固有频率的影响。当橡胶板厚度较小时,由于(2,1)阶模态不改变腔内气体体积,空气弹簧的效果可被忽略,同时板自身属性和预张力提供的等效刚度较小,使(2,1)阶模态将最先被激发出。为更准确对比本文推导的近似方法,计算过程中将板厚为10 mm的模型作为比较基准,确保(1,1)阶模态对应橡胶板的基频振动。该模型其余参数与Amabili等研究的模型均保持一致,为模拟橡胶板在水下工作的情况,附连水质量通过质量点方式附加于板上。控制3个主要设计参数的变化,分别计算模型的(1,1)阶模态固有频率,结果如图5所示。
分析3个设计参数对固有频率的影响,可得到以下规律:
(1)随着橡胶板厚度的增大,橡胶板的一阶固有频率逐步增大,但固有频率总体变化幅度较小,在选取橡胶板厚度时应主要从控制橡胶板静挠度及自身振动响应的角度出发。
(2)随着橡胶板预张力的增大,其一阶固有频率有较为明显的提高,橡胶板预张力对固有频率影响较大,在避振穴设计中可通过调节橡胶板预张力获得所需的固有频率。
(3)随着腔内气体净压强的增大,其一阶固有频率逐步增大,但由于腔内气体净压强不可过大,以防橡胶板变形过大,故在考虑的充气气压范围内固有频率变化幅度较小,在避振穴设计中对腔内气体净压强的选取同样应主要从防止橡胶板变形过大考虑。
此外,图5中各理论计算结果与有限元结果均较为接近,理论计算值总体偏小,但误差均在10%以内。

(a)板厚对基频的影响
2 简化隔振模型计算
首先建立单自由度振动系统,简化模拟船舶在无避振穴条件下,直接受到螺旋桨激励力作用而产生振动,其计算结果可作为后续两自由度系统隔振计算的比较基准,分析加装避振穴后船体振动性能的优化效果。对于图6所示的单自由度振动系统,其运动方程为
(17)
设简谐激振力F(t)=F0·eiωt,位移响应x10满足关系式x10=A10ei(ωt+θ10),可得
(18)


船舶加装避振穴后,螺旋桨脉动压力将首先作用在避振穴上,经避振穴减振后再传递到船体结构。据此,在图6的单自由度振动模型基础上,建立如图7的两自由度隔振模型,在船体m1与激励之间插入避振穴结构m2,模拟避振穴的工作原理。该系统的运动方程式为
(19)
采用复数形式求解,可得

(20)
由于避振穴结构的刚度、阻尼、质量均远小于船体(即k2< (21) 在设计过程中,主要关注船体的峰值响应,即外界激励ω等于或接近船体自身固有频率ω1的情况。此时,对比未加装避振穴的船体响应,可得加装避振穴后响应放大系数α为 (22) 在某318 000 DWT超大型油轮上加装避振穴,分析避振穴应用于实船的减振效果。该船采用单机单桨推进方式,螺旋桨叶频和倍叶频分别为4.233 Hz和8.467 Hz。根据中国船级社《船上振动控制指南》[19],脉动压力主要分布范围为螺旋桨上方d×d区域,在设计初期可采用Holden方法进行估算。计算可得在叶频处螺旋桨脉动压力最大值为1 506 Pa,倍叶频处脉动压力为叶频处的一半,叶频以下频段采用激励力与螺旋桨转速成三次方的关系进行换算,叶频至倍叶频段采用线性插值,倍叶频以上则统一取为倍叶频处脉动压力,如图8所示。 计算模型选取该超大型油轮尾部区域,包含上层建筑及第五货油舱,整体为纵骨架式结构。其中,板结构采用S3及S4R单元模拟,梁、柱结构采用B31H单元模拟,网格间距取为肋距,且在上层建筑部分进行加密。设备质量采用质量点以MPC(multi-point constraints)方式连接到相应节点,舱内油水质量以及舷外水质量通过质量点的形式分布在舱室及船底外板对应位置。螺旋桨激励力采用表面压力方式加载,并在截断横舱壁处施加固支约束条件。采用模态叠加法计算倍叶频范围内尾部结构的响应,并选取艉封板顶部、烟囱顶部、罗经甲板前端、翼桥端部等易发生较大振幅处的节点作为评价点,如图9所示。各评价点原有的速度和加速度频响曲线如图10和图11所示。 从图10和图11可知:各评价点的加速度响应在计算频段内较小,而速度响应在低频段的3.2 Hz和4.6 Hz附近会出现两个较为突出的峰值,分别对应了尾部整体垂向三阶振动以及烟囱上建局部纵向振动的固有频率。其中,在略高于叶频的4.6 Hz附近出现速度响应的极大值,在后续设计避振穴过程中着重考虑减小该频率范围附近的船体振动。 在该超大型油轮尾部螺旋桨上方进行局部结构的修改。以螺旋桨盘面为中心,采用橡胶板代替盘面上方d×d区域的船底板,并向上挖出平均深度约为d的空腔。由于该船尾部接近U型尾且向上收缩,而橡胶板需要绷紧铺设,故适当调整了尾部型线,如图12所示。为防止橡胶板初始变形过大,腔内气体净压强不可过高,同时应适当增加橡胶板厚,并设置足够大的初始预张力。针对该船,设置避振穴腔内气体净压强Δp=0.001 MPa,橡胶板厚h=100 mm,初始预张力fx=fy=1.0 MPa。 图12 实船模型避振穴设计布置Fig.12 Design of anti-vibration cave on real ship model 采用式(16)计算该船避振穴橡胶板的一阶固有频率,可得近似计算值为0.259 Hz,远低于船体响应峰值频率,根据第2章的分析预计可有效减小4.6 Hz附近船体的有害振动。采用ABAQUS软件进行有限元计算,求得橡胶板基频为0.257 Hz,与理论计算值之间的误差仅为0.77%。此外,橡胶板充气后最大静挠度约为0.057 m,对船体表面型线影响较小。 计算该船尾部结构在加装避振穴前后的模态特性,如表3所示。可见船体尾部整体模态的固有频率基本不变,避振穴的改造设计不会使尾部总体模态发生明显变化。 表3 尾部整体模态固有频率Tab.3 Natural frequency of global stern modes 计算评价点的速度响应,结果如图13所示。总体而言,在加装避振穴以后,各评价点在计算频段内振动响应均有较为明显的下降。采用插入损失定量评价避振穴的隔振性能,其计算公式为 (23) 式中:a0、v0为原结构的加速度和速度响应;a、v为加装避振穴后对应节点的加速度和速度响应。计算可得各评价点在原速度响应最为严重的4.6 Hz附近插入损失均达到5 dB以上,其中节点位于罗经甲板前端和翼桥端部的的节点插入损失接近7.5 dB,而在计算频段内其余响应峰值处插入损失也达到了7 dB以上,即加装避振穴可有效减小原结构的振动响应,获得理想的减振效果。 (a)节点5677 本文推导了避振穴固有频率的计算方法,分析了避振穴的减振原理,并以318 000 DWT超大型油轮为例进行了实船避振穴设计和仿真验证,主要得到以下结论: (1)本文推导的近似计算公式可较为准确地预报避振穴的固有频率;通过改变橡胶板预张力可有效调节避振穴固有频率,对橡胶板厚及腔内气体压强的选取则应主要从控制橡胶板静挠度的角度出发。 (3)加装避振穴对船舶尾部原有的模态特性影响很小,可有效降低结构在关注频段的峰值响应,具有良好的减振效果。
3 实船尾部避振穴设计计算
3.1 实船参数及原有振动特性


3.2 避振穴设计

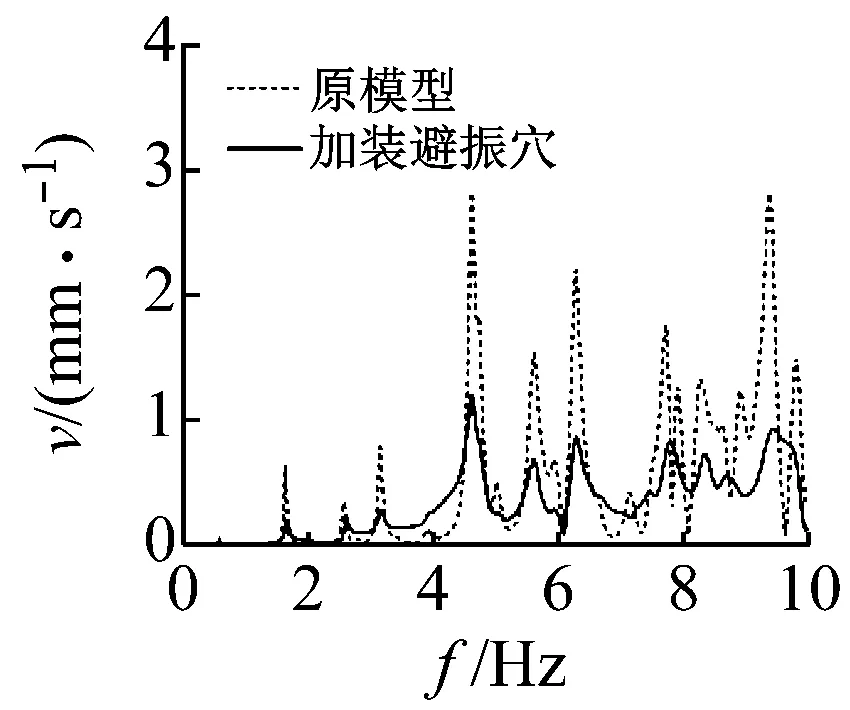
3.3 减振效果分析
4 结 论


