新型橡胶-电磁复合主被动隔振器研究

任明可，谢溪凌，黄志伟，张志谊

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240；2.上海交通大学 振动、冲击、噪声研究所，上海 200240；3.中国舰船研究设计中心，武汉 430064)

大型动力设备，如柴油机、汽轮发电机组等是船舶振动噪声的主要来源之一，对于舰船而言，往复或旋转机械产生的低频线谱振动对舱室噪声和舰船水下声学特征具有重要影响[1]。被动隔振技术，如单层隔振、双层隔振[2-4]和浮筏隔振[5-6]等，能有效地隔离船舶机械设备振动向基础的传递，但被动隔振对低频振动尤其是对声学特征具有重要影响的低频线谱振动的隔离效果并不显著。为获得宽频带隔振效果，应考虑被动与主动结合的方式，即采用被动方式隔离中高频振动，主动方式抑制低频线谱振动。

由于大型动力设备的质量往往在数十吨以上，因此要求主被动隔振器可承受重载，且能产生较大的主动控制力，然而隔振器的允许安装空间又十分有限，限制了主被动隔振器的尺寸。现有公开的主被动隔振器多采用组合式设计，即被动和主动器件安装于公共底座上。钱炫言等[7]将橡胶隔振器集成于电磁作动器内部，结构紧凑，出力较大，但被动隔振部分承载能力有限；Li等[8]将作动器集成于空气弹簧内部，可以承受重载，但悬浮间隙需要通过空气弹簧调整；王俊芳[9]将橡胶隔振器和电磁作动器堆叠，可以承受重载，但总高难以适应有限的安装空间；Wang等[10]提出一种支腿内部嵌有压电作动器的立方体Stewart隔振平台，适用于轻载微振动的控制。

主被动隔振中的控制方法包括最优控制、鲁棒控制[11]、自适应控制[12-15]等，其中自适应算法中的递推最小二乘算法和最小均方误差(least mean square,LMS)算法等，自适应能力强，易于硬件实现，广泛应用于工程实践中。在基于LMS算法的一系列衍生算法中，干扰重构Fx-LMS(filtered-x least mean square)算法[16]具有良好的线谱控制效果。在实践中，由于系统的频响特性复杂，使得基于脉冲响应的自适应算法在整个频带内的控制效果没有一致性，往往存在部分频段控制效果较差的问题。

本文针对重载设备宽频带隔振需求，提出一种低频被动隔振器与线性电磁作动器复合的新型主被动隔振器，以更好地衰减中高频振动和低频线谱振动，此外，在干扰重构Fx-LMS算法的基础上，给出频域加权的自适应算法，以获得全频段的主动控制效果。本文主要内容包括隔振器特性分析、作动器力常数测试、控制算法及隔振效果试验。

1 主被动隔振器结构

主被动隔振器结构,如图1所示。该隔振器外部为剪切式橡胶隔振器，橡胶选用邵氏硬度为65 HA的丁腈橡胶，采用双层串联结构，上下橡胶层之间为惯性体，电磁作动器安装于橡胶隔振器内部空腔，其导磁体外壳与被动隔振器的惯性体相连。导磁体和永磁体可视为作动器的定子，线圈及其支架可视为作动器的动子。线圈支架与隔振器上端面连接，使线圈悬吊于工作位置。电磁力作用于负载和惯性体之间，实现主动控制。

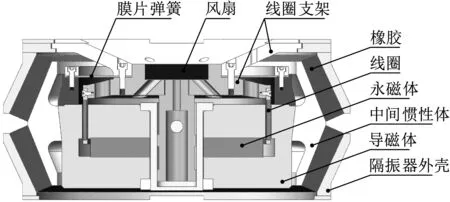
图1 主被动复合隔振器结构示意图Fig.1 Schematic of the passive/active vibration isolator

这种复合隔振器构型紧凑，兼顾了被动承载和内部空间利用，而且作动器定子与惯性体结合，有助于提高被动隔振器的高频衰减性能。此外，作动器控制力直接作用于惯性体，路径控制相对集中，而作动器的无效高次谐波可被橡胶隔振器吸收，以利于抑制控制力失真，提高主动控制效果。

2 橡胶隔振器特性

2.1 橡胶隔振器静特性

用于橡胶隔振器静特性分析的有限元模型,如图2所示。其中橡胶材料为非线性超弹性体，应力应变关系以两参数Mooney-Rivlin模型进行描述。静力分析时，隔振器下端固定，上端逐渐加载至额定载荷15 t，加载步长为1 t，提取隔振器上端面垂向位移，可得力-位移曲线。橡胶隔振器静特性加载测试系统,如图3所示。下端面固定，上端均匀缓慢加载至150 kN，测得橡胶隔振器垂向力-位移曲线，将其与有限元计算结果对比，如图4所示。可见测试与仿真结果较为接近，且隔振器线性度较好。由计算和测试结果可知，当加载到15 t时，橡胶隔振器的静变形约为14.73 mm。对实测曲线拟合并求导，可得隔振器的静刚度-位移曲线，15 t静载下的静刚度约为1.38×107N/m。需要说明的是，有限元模型主要用于橡胶隔振器的参数设计。

2.2 橡胶隔振器隔振性能

橡胶隔振器被动隔振性能测试系统,如图5所示。隔振器安装于弹性基础上，负载质量为2 000 kg，使用激振器施加随机激励，传感器拾取负载及基础上的振动信号，经处理后得到振动传递率，如图6所示。为从理论上描述该曲线，隔振器及其负载可以简化为两自由度模型，如图7所示。膜片弹簧刚度忽略不计，振动传递率的计算公式可表示为

(1)

式中：ML为负载质量;Mi为中间惯性体与作动器定子质量之和,约80 kg;kr(1+jηr)为橡胶层复刚度。

根据实测的传递率，可拟合出橡胶层在2 000 kg负载下的动刚度kr约为6×107N/m，橡胶隔振器动刚度约为2.97×107N/m。图6的测试结果符合两自由度隔振特征，由于两层橡胶之间为中间惯性体，并与电磁作动器定子结合，提高了隔振器的高频隔振性能，这是本文主被动隔振器的一 特点。

3 电磁作动器力常数

力常数测试系统,如图8所示。动态信号测量系统发出随机激励信号，经功率放大器驱动主被动隔振器内部的电磁作动器，位于负载上端和弹性基础上的两个加速度传感器测量振动响应，得到频响曲线如图9所示。该曲线反映了激励电压和加速度响应之间的关系。由于功率放大器的激励电压与输出电流之间有确定关系，只要获得力与加速度响应之间的频响曲线，即可确定力与作动器输入电流之间的关系，即力常数。为此，借助理论模型，将测试系统简化为三自由度模型，如图10所示。其中弹性基础采用单自由度模拟。对该模型进行动力学分析，可获取力-加速度频响函数。

图8 力常数测试系统Fig.8 Force constant testing system

(a)

图10 测试系统简化模型Fig.10 Simplified model of force constant testing system

kr(1+jηr)(Xi-Xb)-F=0,

(2)

控制力作用下，隔振器上端(负载)及隔振器下端(弹性基础)的加速度响应可表示为

(3)

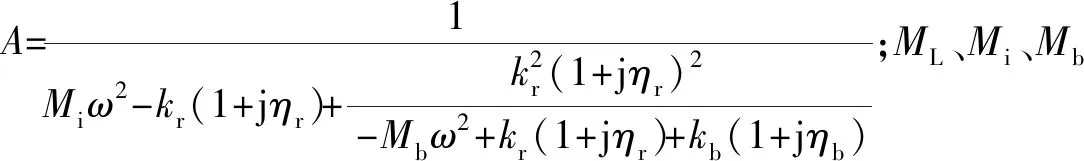
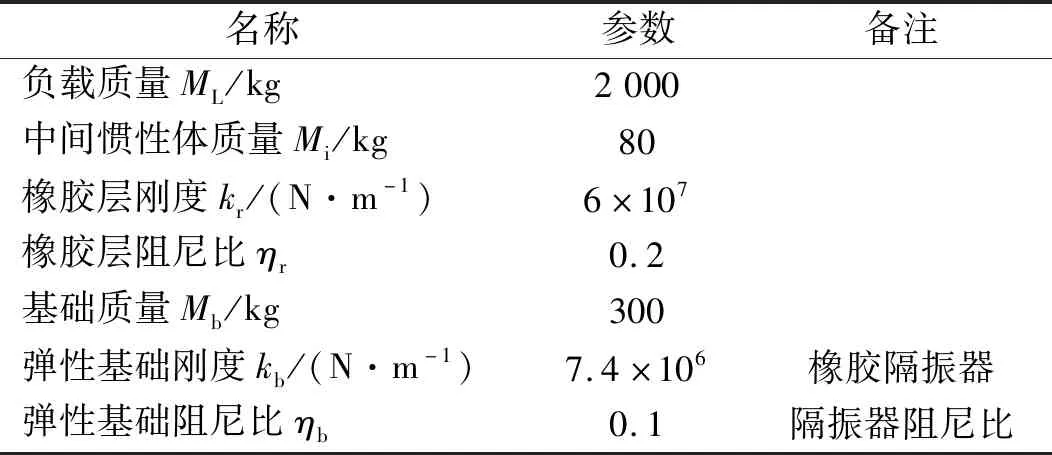
表1 模型参数表Tab.1 Parameters of the model

可利用重合段的频响曲线估计力常数。由于作动器控制力Fa=2πRNBI，其中:R为线圈半径;N为线圈匝数;B为磁场磁感应强度;I为线圈电流。即作动器控制力与线圈电流成正比，同时考虑到功率放大器的激励电压与其输出电流有已知的正比关系，实测的电压-加速度响应曲线可以转换为电流-加速度响应曲线。由此可计算控制力与电流之间的比例常数，该常数约为72 N/A。

4 主被动隔振效果

4.1 频域加权Fx-LMS自适应控制算法

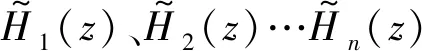
(a)

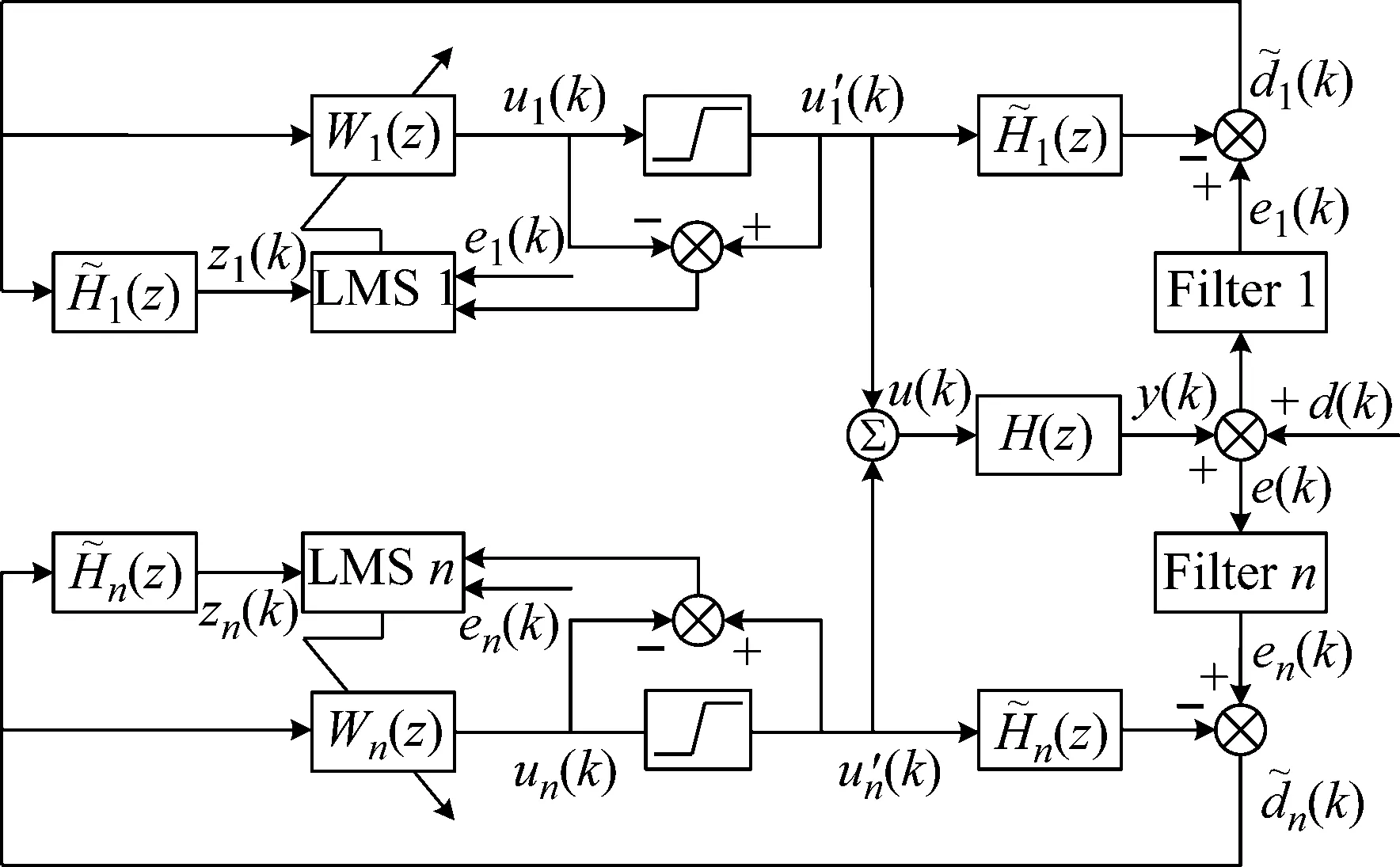
图12 频域加权Fx-LMS自适应控制算法Fig.12 Frequency domain weighted Fx-LMS algorithm

(4)

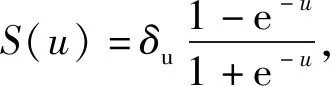
4.2 主被动隔振性能

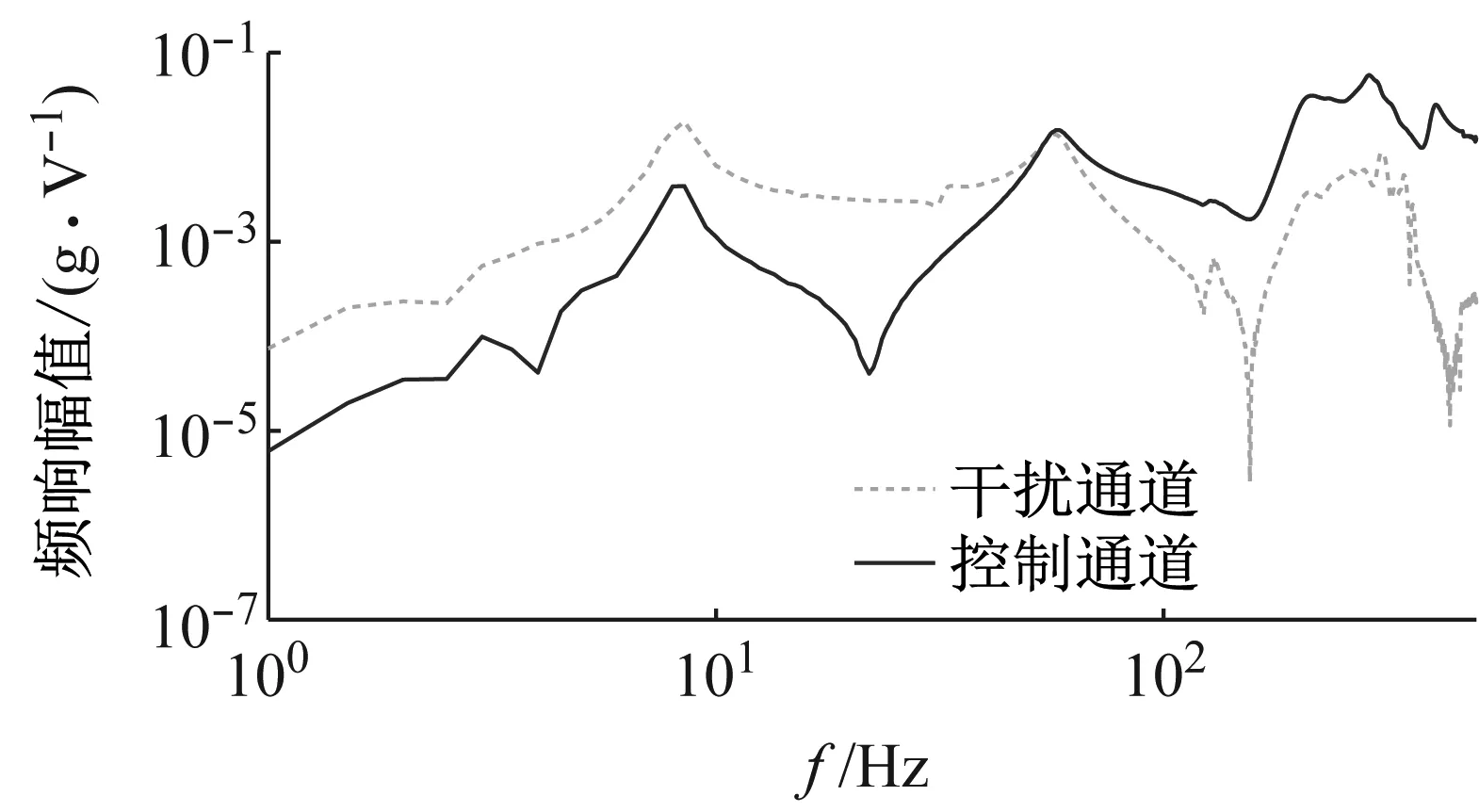
主被动隔振测试系统,如图13所示。隔振器安装于弹性基础上，基础下方联接激振器，对基础施加激励。负载和基础上分别布置加速度传感器，其中负载的振动加速度响应作为控制误差信号，经信号调理器滤波放大后输入控制系统，控制器根据加权自适应控制算法产生控制信号，输出至功率放大器，驱动主被动隔振器内部的电磁作动器，实现主动隔振。误差点处控制通道、干扰通道频响,如图14所示。可见控制通道的幅频特性变化较大，尤其在22 Hz附近，控制通道存在反共振点，可控性较差，因此需要使用频域加权Fx-LMS自适应控制算法，提高该频段的控制效果。

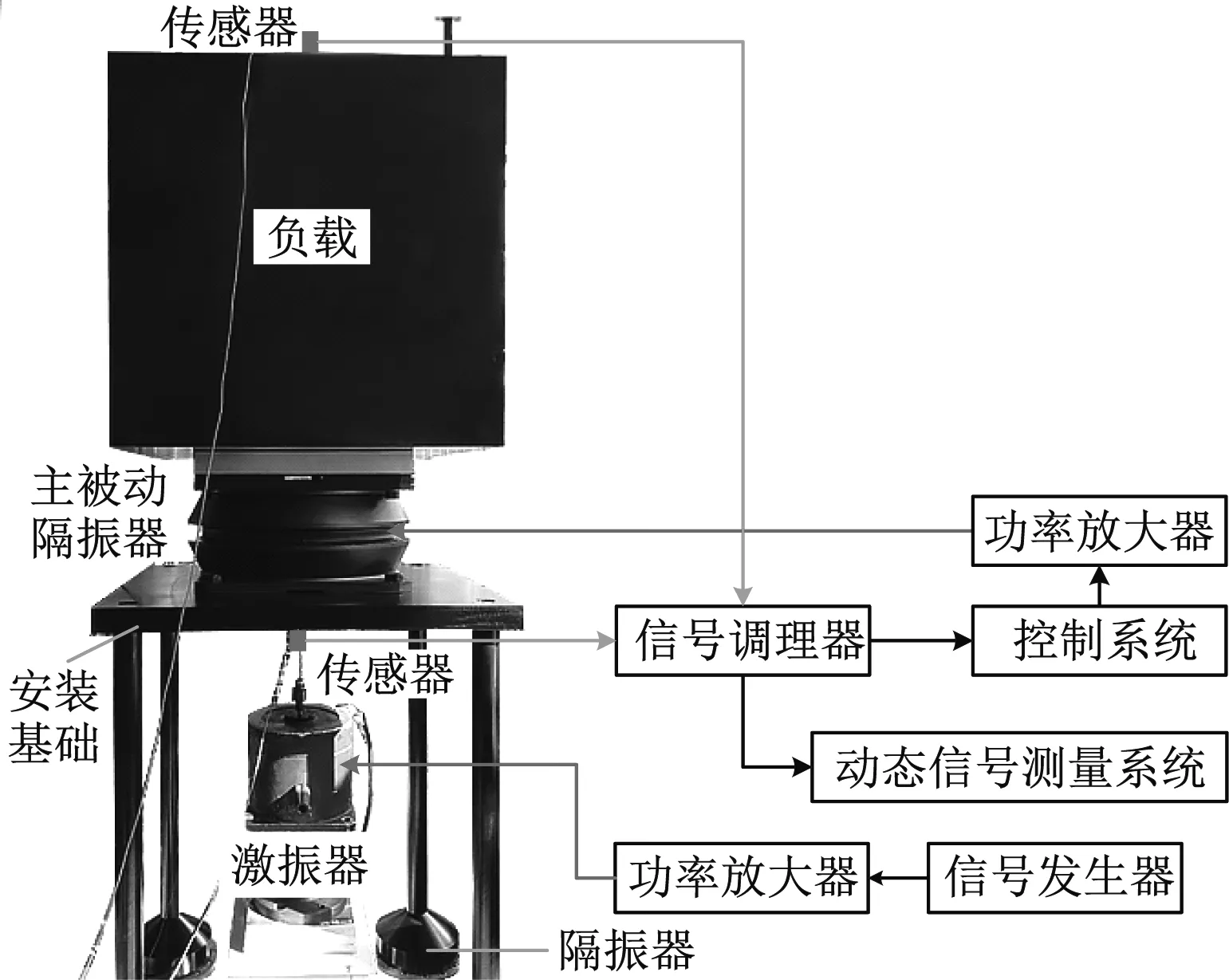
图13 主被动隔振测试系统Fig.13 Passive and active vibration isolation performance testing system

为了验证主被动隔振器性能，激振器发出宽频随机激励叠加一组线谱激励(频率分别为30 Hz、60 Hz、90 Hz、180 Hz、240 Hz)，同时控制算法对300 Hz以内振动进行控制。纯被动和主被动隔振下的负载振动如图15所示，受隔振频率限制，被动隔振在低频段的衰减量较小，随着频率的增加，被动隔振衰减量逐渐增大(除响应较低的频段外)，自30 Hz开始，衰减由3 dB逐渐增大到40 dB以上，与图6所示的规律相一致；主动隔振后，线谱特征均明显下降，衰减量如表2所示。其中30 Hz处尽管可控性较差，使用频域加权Fx-LMS算法后，线谱幅值依然衰减38 dB，其余线谱衰减均达50 dB以上。为评价总体隔振效果，在5～300 Hz频带内，纯被动隔振使负载振动总级衰减约18 dB，施加主动控制后，负载振动总级衰减达49 dB。

(a)

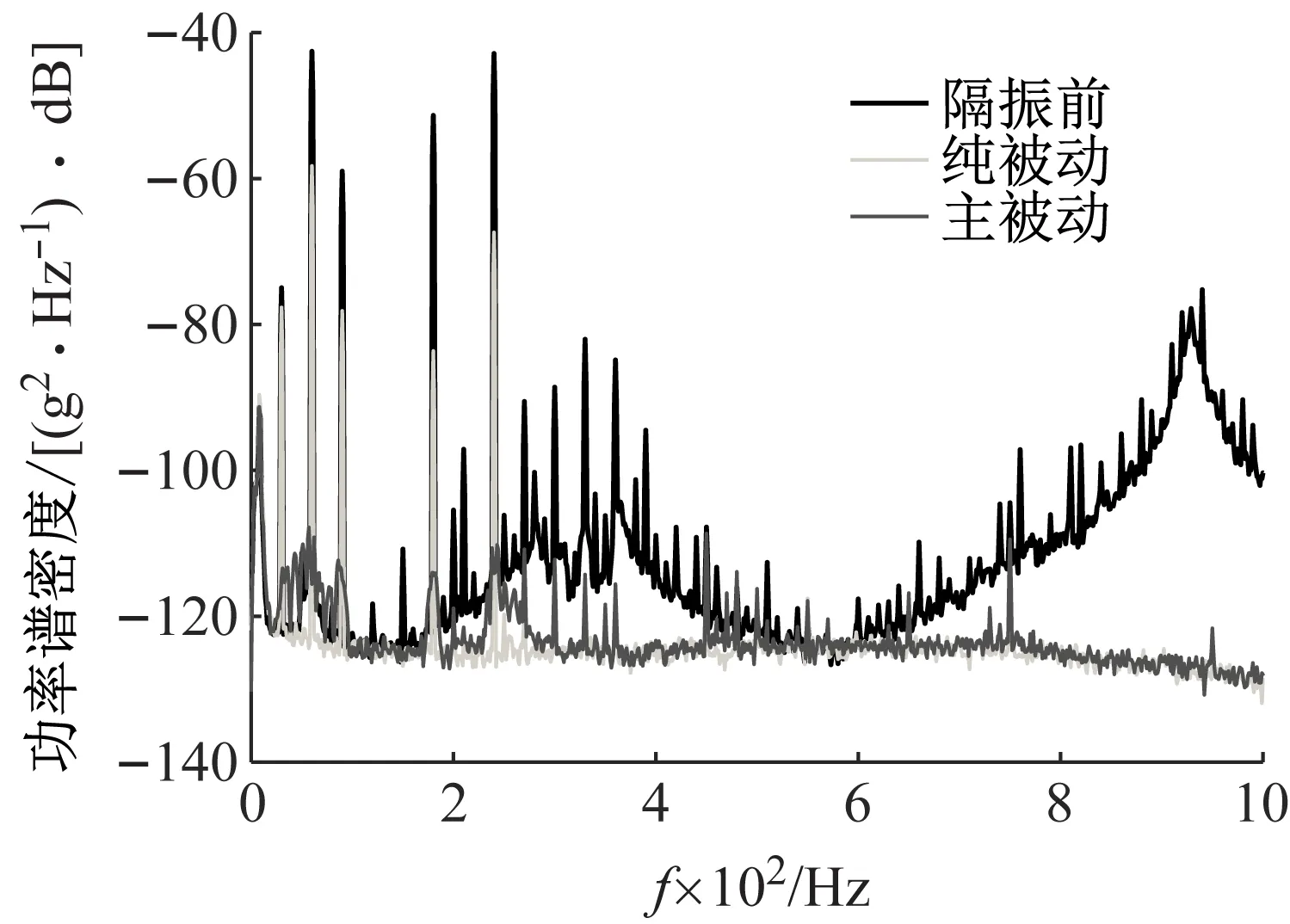
图15 主被动隔振效果Fig.15 Passive and active vibration isolation performance

表2 线谱振动衰减量Tab.2 Attenuation of harmonics [(g2·Hz-1)·dB]

5 结 论

本文提出了新型主被动复合隔振器，并通过理论计算和试验获得了主被动隔振器性能，主要结论如下：

(1)隔振器充分利用了被动与主动部分的惯性效应，具有二自由度系统隔振特性，提高了高频段隔振性能。

(2)通过间接测试方法获得了电磁作动器的力常数，输出力的有效值可达700 N。

(3)提出频域加权自适应方法并应用于主动隔振，使得作动器能够有效衰减低频段线谱振动的传递，线谱衰减量可达30 dB以上。

(4)试验结果表明，主被动复合隔振效果显著，在5～300 Hz频段，振动总级衰减可达49 dB，远高于纯被动隔振效果。