一种改进的WorldView-2遥感图像融合方法

李 涛，王红军，李 甲，杜 阳

(1.河南科技学院新科学院 电气工程系，河南 新乡453003；2.北京大恒图像视觉有限公司，北京 100193)

近年来，新型卫星遥感多光谱图像的波段在不断增加，图像的分辨率也在快速提高。以WorldView-2(WV-2)卫星为例，它能够提供8波段1.84 m分辨率的多光谱图像和单波段0.46 m分辨率的全色图像。与传统卫星图像相比，WV-2卫星具有以下特点：波段增加，光谱划分更细；全色图像的光谱覆盖范围变窄，使之与多光谱波段的光谱匹配发生较大变化。在遥感应用上，往往需要同时具有高空间和高光谱分辨率的图像。图像融合技术就是利用高空间分辨率的全色图像去提高多光谱图像的空间分辨率，同时尽量保持多光谱图像的光谱特性不变。WV-2卫星图像代表了超高分辨率遥感图像的发展趋势，同时也对遥感图像的融合提出了更高的要求。

WV-2卫星的光谱波段分布情况见表1。由表1可以看出多光谱与全色图像的波谱覆盖范围，多光谱的8个波段中有3个波段没有被全色波段覆盖，多光谱与全色光谱响应也不一致，正是这些特性导致融合结果变差。

表1 WorldView-2卫星光谱波段分布Tab.1 Spectral band distribution of WorldView-2 satellite nm

Pan-sharpening算法是图像融合算法的主要分支，也是遥感图像融合的一种重要方法[1]。在几十年的发展中，Pan-sharpening技术在不断改进，例如给予多分辨分析[2]的算法。随着深度学习的应用和发展，深度学习也被运用到图像融合中，例如Huang等[3]提出了深度神经网络(deep neural network,DNN)算法，但该方法偏离了Pan-sharpening算法的原理。随后，Masi等[4]提出了基于卷积神经网络的Pan-sharpening算法，符合Pan-sharpening算法原理，但该算法网络结构过于简单，提取特征不够深入。Wei等[5]提出了基于深层残差神经网络的Pan-sharpening算法，通过11层残差网络提取输入图像的深层特征。蔡婉婷[6]提出了基于多层耦合卷积网络的 Pan-sharpening 算法和基于耦合多尺度网络的 Pan-sharpening 算法，利用卷积自编码器提取图像特征，保证图像块的空间信息不被破坏。基于深度学习的融合算法复杂度较高、设计不易，目前处在研究阶段，应用较少。文献[7]首次提出了基于平滑滤波的亮度模型(SFIM)融合方法，这种方法可以快速融合数据量较大的遥感图像，是一种增加空间细节信息的光谱保持型图像融合方法，是依据简化的太阳辐射和地表反射模型提出的一种光谱保持型融合技术，然而对于新型卫星如WV-2，其融合过程容易导致光谱畸变。为减少SFIM方法对滤波器的依赖及在新型卫星图像融合过程中容易出现的问题，文献[8]提出了一种改进算法MSFIM。该文通过分析RGB-HIS变换模型对SFIM算法进行了一种新的解释，得出了SFIM融合算法的结果，即亮度分量与全色图像不同、光谱信息无变换，说明SFIM方法的光谱保持较好而细节融入与全色图像发生了变化。然而，该改进算法没有考虑多波段图像波段之间的不同。

除SFIM融合方法外，目前较流行的还有HIS变换，但HIS变换对波段有限制。因此，Tu等[8]提出了一种Fast HIS方法。另外，DigitalGlobe公司的Chris等[9]提出了一种新的Pan-sharpening方法，该方法无波段限制，首先进行RGB-HCS空间变换，然后在HCS空间进行亮度分量替换，再反变换到RGB空间。李旭等[10]提出了一种基于对应分析的WV-2图像融合算法，此方法先将八波段多光谱图像变换至成分空间，然后通过成分图像将全色图像的空间细节信息注入成分空间，经反变换后得到融合结果。然而，Tu等[11]对Chris的方法进行了分析，证明此方法实际上是一种与Brovey变换类似的方法。此外，还有传统的小波变换、主成分分析等融合方法，但这些方法在新型卫星WV-2图像融合中都存在光谱畸变和细节融入难的问题[12-13]。

针对WV-2卫星图像融合存在的问题，本研究提出了一种基于SFIM的改进算法。考虑到WV-2卫星图像各波段光谱响应的不同，本研究在MSFIM方法[2]的基础上增加了一系列参数，设想各波段一定存在一个最佳的权值使融合结果达到最佳。实验结果证明这样的设想是正确的，确实找到了这样一组参数，最终得到了高质量的融合结果。

1 亮度平滑滤波调制融合方法(SFIM)

SFIM融合方法是由Liu[7]在2010年提出的一种比值融合方法。该方法在传统的图像融合中能够快速进行融合并能保持图像的光谱特性不变，通过全色图像与全色低频图像的比值获取地形和高频细节信息，再将这些高频信息融入多光谱图像中[14]。然而，这种方法对产生Panlow的低通滤波器依赖较大，不同的低通滤波器可能导致结果有较大差异。该算法如下：

(1)

式中：Panlow由全色图像Pan经过平滑滤波得到；Band1，…，Bandn为多光谱图像的各个波段；Band1SFIM，…，BandnSFIM为融合后的多光谱图像的各个波段。

融合时，首先将多光谱图像插值到与全色图像同样大小，然后与全色图像和低通滤波后的全色图像进行式(1)的计算。SFIM方法在传统的三波段多光谱图像融合中能够得到较好的结果，但随着多光谱图像波段的增加，它已不能满足多波段图像的融合要求。由于WV-2卫星遥感图像的全色与多光谱各个波段的光谱响应特性不再与传统卫星一样，所以传统的融合方法很难适应WV-2遥感图像的融合。

2 改进的SFIM融合方法

SFIM方法要想得到较好的融合效果，必须设计一个性能较好的低通平滑滤波器[15-16]，以得到较理想的Panlow。设计一个性能卓越的滤波器也是一件困难的事情，即使得到了一个性能卓越的滤波器，面对新型卫星遥感图像的特点，融合结果也难免不理想。为减少SFIM方法对滤波器的依赖，并使其能适应WV-2卫星图像的融合，提出以下改进方法：

(2)

该方法是在MSFIM方法基础上提出的。MSFIM是在SFIM基础上改进的算法，然而MSFIM没有考虑各个波段之间的差异。考虑到多光谱图像各个波段的差异，增加了系数k1,…,kn，并通过实验寻找最佳系数，从而改善融合效果。

I是从多光谱图像中提取的亮度分量，本实验针对WorldView-2图像融合采用I=(B+G+Y+R+RE+NIR1)/6。B、G、Y、R、RE、NIR1分别代表WV-2多光谱图像的蓝、绿、黄、红、边缘红、近红外1波段，k1,k2,…,kn为每个波段的常数系数。根据不同的融合需求可以选择不同的系数，选择不同的系数可使细节融入最好或光谱保持最好，亦可使细节融入和光谱保持综合效果达到最好，该系数可以通过实验确定。如果可以改变亮度分量I和系数k1,k2,…,kn，那么本方法也可适用于其他新型卫星图像融合。

3 实验及结果分析

为验证算法的正确性和优良性，用两组真实的WV-2图像数据进行融合实验：第一组为Sydney Australia, 4/3/2011，第二组为San Clementa California USA，3/21/2012。这里只融合WV-2的八波段多光谱图像中的红、绿、蓝和近红外波段，其他波段可用同样方法操作。实验截取部分数据，大小为300×300，灰度级为256。为获取主观评价融合结果的参考图像，首先把多光谱和全色图像下采样到原来的四分之一，再把多光谱图像上采样到原来大小，这样参与融合的全色图像与多光谱图像就有相同的大小，原始多光谱图像就可以作为参考图像用于融合结果的评价[17]。

3.1 第1组数据的实验

表2给出了不同波段在k取不同值时的相关系数。表2中CC1表示光谱相关系数，CC2表示细节相关系数，其前面的修饰表示不同波段，如BCC1表示蓝波段的光谱相关系数。根据一定的先验知识，实验中k值从0取到1.5，步长为0.1，从而找出最佳值。步长太小，数据变化缓慢易导致融合结果变化不明显，会增加实验工作量，步长太大又容易丢失最佳取值，故取步长为0.1。在此，仅用光谱相关系数和细节相关系数作为标准来寻找k的最佳值，因为这两个准则能够很好地反映融合结果。

表2 数据1不同k值融合结果的相关系数Tab.2 Correlation coefficients of fusion results of different k values for data 1

从表2可以看出，正如设想的那样，每个波段图像的融合结果在使CC1或CC2达到最大时都有自己的最佳k值，例如蓝波段k=0.2时有最大BCC1(0.941 066)，k=1.3时有最大BCC2(0.849 153)。

3.2 第2组数据的实验

从第2组数据的实验结果(表3)中可以看出，数据2得到了与数据1相同的结果，证明了该改进算法的正确性和稳定性。

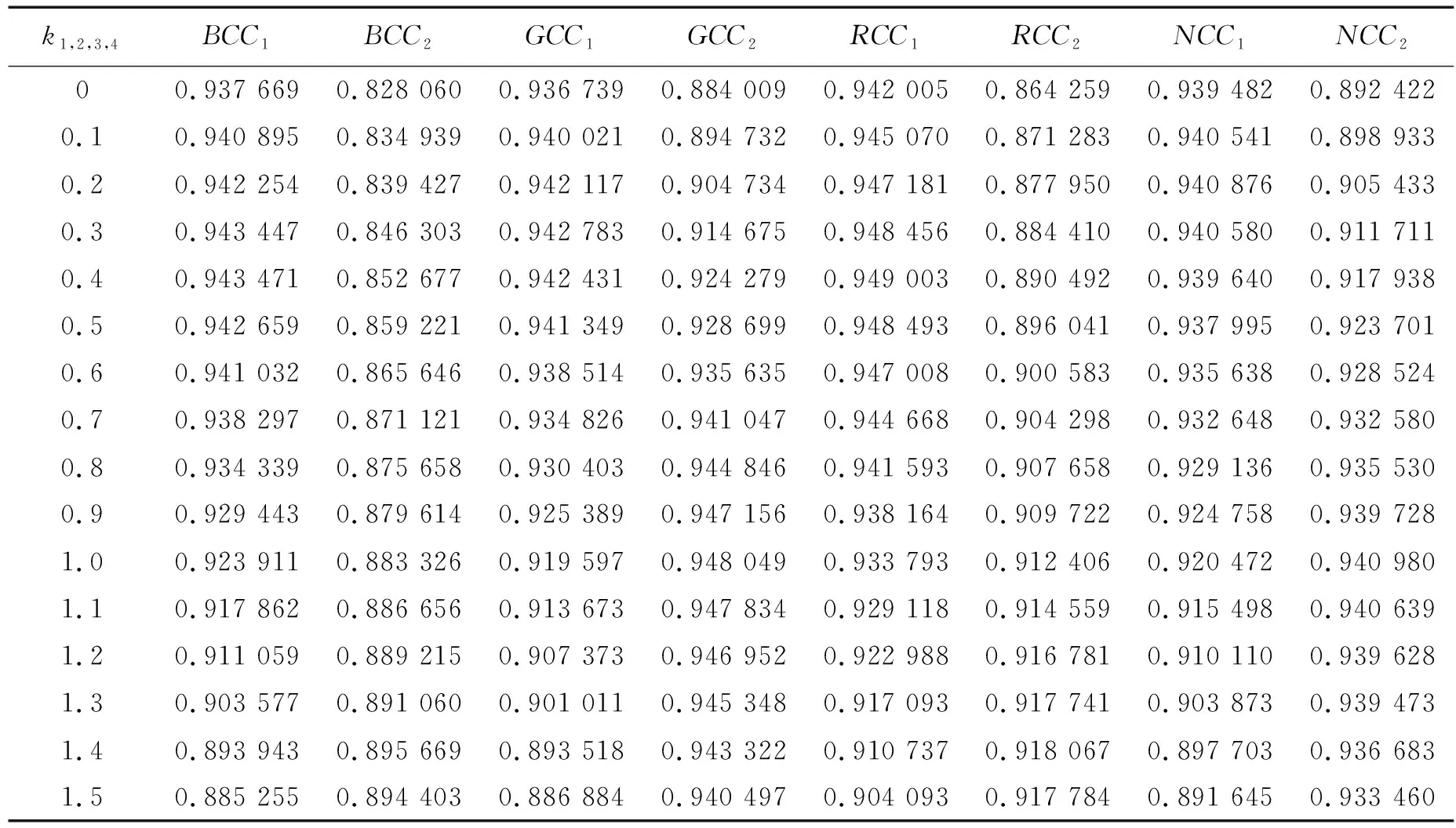
表3 数据2不同k值融合结果的相关系数Tab.3 Correlation coefficients of fusion results of different k values for data 2

3.3 结果与分析

为证明改进算法的有效性，对以上两组实验数据进行分析。综合计算表2和表3可得表4与表5。

表4 两组数据各波段CC1最大时的k值Tab.4 The k value at the maximum of CC1 in each band of the two groups of data

表5 两组数据各波段CC2最大时的k值Tab.5 The k value at the maximum of CC2 in each band of the two groups of data

表4列出了数据1和数据2各个波段获得最大CC1时的最佳k值；表5列出了数据1和数据2各个波段获得最大CC2时的最佳k值；对两个相关系数求和，得到使CC1与CC2之和达到最大的k值(表6)。

表6 两组数据各波段CC1与CC2之和最大时的k值Tab.6 The k value at the maximum sum of CC1 and CC2 in each band of two groups of data

从表4至表6可以看出两组数据的最佳参数k比较接近或者相同。例如表4中CC1最大时两组数据各个波段的k值相差不超过0.2，证明该改进算法具有通用性，是可行的。根据融合图像使用情况的不同，可以选择表4、表5或表6中的k值。如果要融合图像有较大的光谱相关性可以选择表4中的参数；如果要融合图像有较好的细节相关系数可以选择表5中的参数；如果要融合图像综合光谱与细节可以选择表6中的参数。

图1给出了数据1改进前和改进后最佳k值时的红、绿、蓝波段组合成的融合图像。

图1 实验数据1及融合图像Fig.1 Experimental data 1 and images of fusion

从图1可以看出，融合图像(c)的光谱保持最好，与原始图像(a)的光谱特性最为相近；融合图像(d)的细节信息融入最为充分；融合图像(e)则具有光谱保持和细节融入的综合优势。图2给出了第2组数据的融合图像，依然是改进前和改进后最佳k值时的红、绿、蓝波段组合成的融合图像。

图2 实验数据2及融合图像Fig.2 Experimental data 2 and images of fusion

从图2可以看出，融合图像(c)的光谱保持最好，与原始图像(a)的光谱特性最为相近；融合图像(d)的细节信息融入最为充分；融合图像(e)则具有光谱保持和细节融入的综合优势。

对两组数据的实验结果进行主观评价，数据1和数据2 的主观评价结果完全一致，即用表4中的系数可以得到光谱保持最好的图像，而用表5中的系数可以得到细节融入较丰富的图像，用表6中的系数则可以得到具有综合优势的融合图像。实验结果证明改进算法提高了图像融合的性能。

4 结语

针对高分辨率的WV-2卫星图像，本研究在SFIM算法的基础上提出了一种改进的融合算法，该算法对图像的波段没有限制，能适应多波段新型卫星遥感图像的融合。为克服SFIM方法存在的缺陷，改进算法对每个波段的亮度进行了修正，且各个波段的修正权系数不同。通过实验确定最佳系数k1,k2,…,kn，给出了3组最佳系数用于不同的融合需求，即最佳光谱保持、最佳细节融入和二者综合的最佳系数。两组实验结果完全一致，主观评价符合客观数据分析，表明了该改进算法的有效性，证实该方法能很好地融合WV-2卫星图像，且可用于其他卫星遥感图像的融合。