基于MATLAB和ADAMS的八字式转向机构优化

韩飞坡，谈 波，李光宇，王 杰，孙 怡

(1.马鞍山学院 智造工程学院，安徽 马鞍山 243100；2.安徽合力股份有限公司安庆车桥厂，安徽 安庆 246001)

转向机构是叉车的关键部件，其结构和尺寸对叉车的转向性能及转向桥的可靠性有着重要影响。叉车转向轮的转角一般较大，故对转向机构有较高的转向要求。八字式双梯形机构是常见的叉车转向机构，与横置液压缸式转向机构相比，该机构结构简单、造价低、环保节能，可以有效避免油缸漏油。众多高校和科研机构对八字式转向机构的转向特性做了大量研究。郭凌汾等[1]推导出了八字式转向机构内、外转向轮转角的计算公式，分析相关参数对转向特性曲线的影响，并提供了一种研究八字式双梯形转向机构转向特性的方法，为八字式转向机构的优化奠定了一定的基础；陈慕忱等[2]采用SUMT优化方法通过FORTRAN程序对八字式转向双梯形机构进行了优化设计，优化后依然存在最大转角误差大、程序烦琐、效率低等问题；陆植[3]对双梯形机构的优化方法进行了探讨；陈学科等[4]运用C++语言编制了八字式转向机构优化程序并对其进行了参数优化，但缺乏对优化模型参数的验证及其他力学性能的研究。本研究结合某公司生产的某型号叉车八字式转向桥的实际需求，建立数学模型，定义最优目标函数，在MATLAB中进行多目标优化设计，通过ADAMS虚拟仿真证明了转向机构数学模型的正确性及优化参数的可靠性，最后通过实物样机验证了优化仿真的准确性。

1 八字式转向机构模型简化及数学模型建立

转向机构简化模型为双梯形机构[5](图1)，右侧A1GED和左侧ABCD均为四杆机构，两个四杆机构之间通过三角板CDE传递运动。该机构在三角板向右绕D点转动的驱动下，DE绕D点转过角度φ，EG杆发生平移和偏转，转向机构由初始状态(图1中的粗实线)转移至某时刻运动状态(图1中的虚线)。此时，内、外车轮转过的角度分别为β、α。

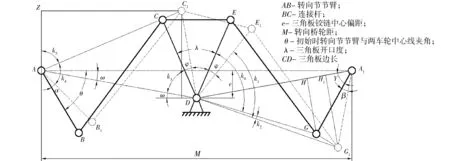
图1 转向机构简化模型Fig.1 Simplified model of steering mechanism

内、外车轮转过的角度β和α之间关系的建立过程如下：

首先，分析初始状态下的转向机构ABCEGA1。

在△A1DA中，AD与两车轮中心线夹角

ω=arctan(2e/M)，

(1)

点A与点D之间的距离

(2)

在△A1HG中，点H与点G之间的距离，以及点A1与点H之间的距离分别为

lHG=lA1Gsinγ，

(3)

lA1H=lA1Gcosγ，

(4)

式中：γ为GA1与DA1的夹角。

在△A1DG中，点D与点H之间的距离

lDH=lA1D-lA1Gcosγ。

(5)

在△DHG中，点D与点G之间的距离

(6)

然后，分析运动后的转向机构AB1C1DE1G1A1。

在△A1H1G1中，

lA1H1=lA1G1cos(γ+β)，

(7)

lH1G1=lA1G1sin(γ+β)。

(8)

在△DH1G1中,点D与点G1之间的距离

(9)

在等腰△A1GG1中，初始状态下点G与运动状态下点G1之间的距离

lGG1=2lA1G·sin(β/2)。

(10)

在△EDG中，初始状态下三角板DE边与DG连线的夹角

(11)

在△E1DG1中，运动状态下三角板DE1边与DG1连线的夹角

(12)

在△DGG1中，初始状态下DG连线与运动后DG1连线的夹角

(13)

则三角板CDE转角φ与各夹角k0、k1、k2的关系为

φ=k0-(k1-k2)。

(14)

在△AC1D中，运动状态下AC1连线距离

(15)

式中：k3表示初始状态下三角板CD边与AD连线的夹角。k3有如下关系：

k3=(π-λ)/2-ω。

(16)

在△AB1C1中，运动状态下C1A连线与AB1连线的夹角

(17)

在△AZC1中，C1A连线与竖直线AZ的夹角

k5=arccos[(lC1Dsin(k3+ω+φ)-e)/IAC1]。

(18)

在左侧转向机构中，有以下关系：

π/2+θ=α+k4+k5。

(19)

综上，即得α的数学关系表达式为

(20)

2 八字式转向机构的优化

四支点叉车转向简图见图2。车辆转向时，若叉车车轮轴线能交于一点，则叉车在转向时各车轮都会做纯滚动运动，这样能够避免车轮轮胎在地面滑动，减少轮胎磨损，延长轮胎的使用寿命。

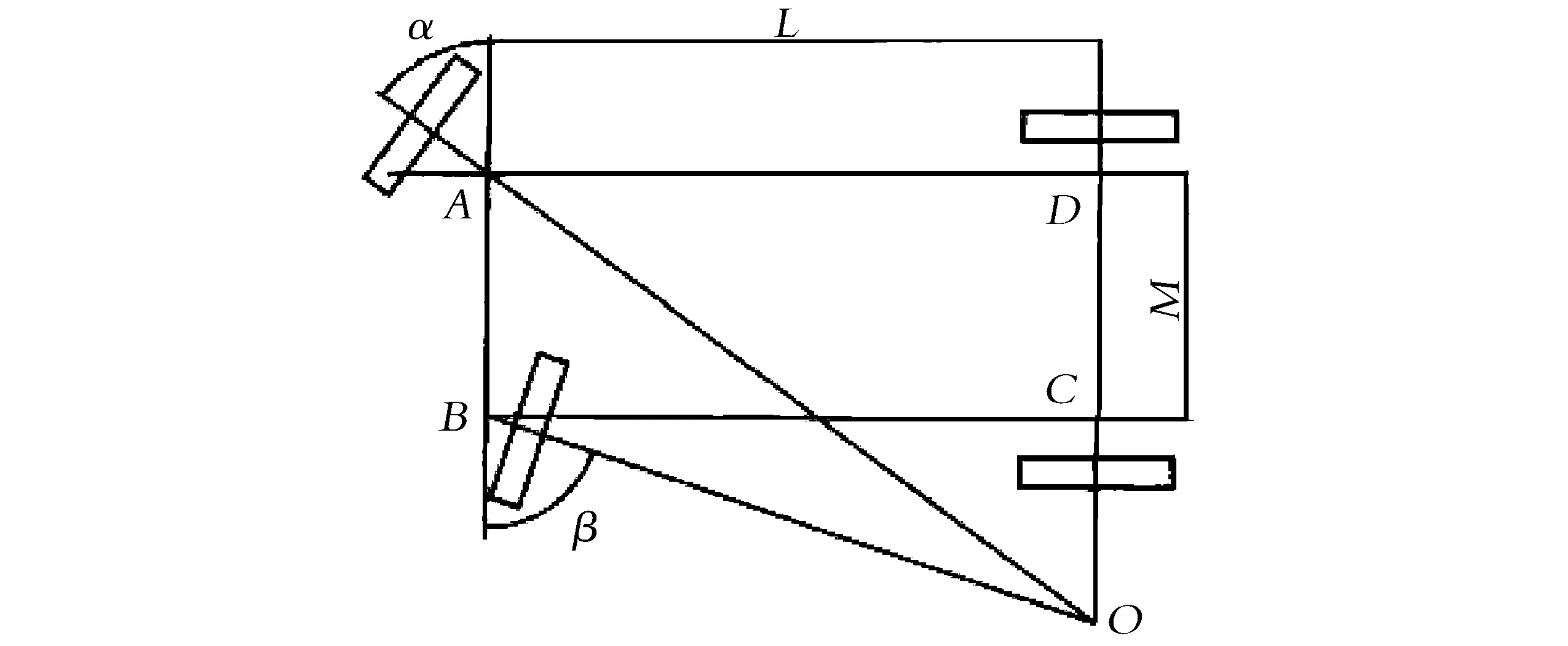
图2 四支点叉车转向简图Fig.2 Four-fulcrum forklift steering diagram

叉车转向时如果内、外车轮只做纯滚动运动，可用下式表示内、外车轮的关系：

cotα-cotβ=M/L。

(21)

根据某公司设计的技术参数，叉车轮距M=920 mm，轴距L=1 920 mm，对该叉车转向机构进行优化分析如下：

(1)转向机构设计变量：转向节节臂长度lAB、连接杆长度lBC、三角板铰链中心偏距e、初始时转向节节臂与两车轮中心线夹角θ、三角板开口度λ、三角板边长lCD。

(2)确定目标函数。转向机构优化目标函数

(22)

式中：f为某一时刻实际、理论外轮转角差绝对值；αi为某一时刻实际外轮转角；αi′为某一时刻理论外轮转角；ωi为权重。

(3)确定约束条件。参考文献[6-8]并结合公司某型号叉车转向桥设计实际情况，设定约束条件如表1所示。使用MATLAB软件进行优化，优化前与优化后数据如表2所示。

表1 八字式转向机构优化变量取值Tab.1 Value range of optimization variables for the splayed steering mechanism

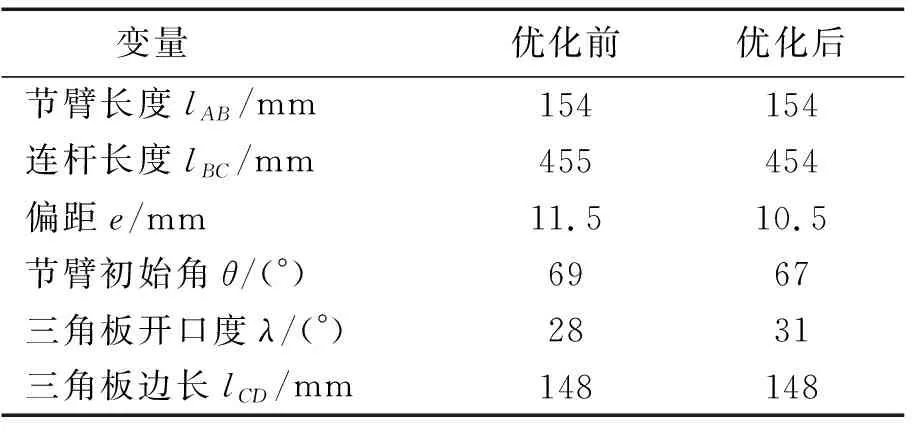
表2 八字式转向机构优化前后参数对比Tab.2 Comparison of parameters before and after optimization of the splayed steering mechanism

3 转向机构模型验证及其力传动性能

3.1 转向机构优化模型验证

根据MATLAB软件优化后的机构尺寸，利用 ADAMS 软件[9]对转向机构进行几何体建模，并施加约束副和驱动副，最终样机模型如图3所示。

图3 八字式转向机构ADAMS样机模型Fig.3 ADAMS prototype model of splayedsteering mechanism

对ADAMS软件优化前后模型的内、外转角及阿克曼转角进行对比，结果见图4。从图4可知，车轮转向时，外侧车轮的转角随着内侧车轮转角的增大也相应增大，优化后的转向特性曲线越来越接近阿克曼理想特性曲线。图5给出了优化后内、外转角转向特性曲线与阿克曼理想特性曲线之间的误差，该误差小于0.8°，在内轮转角为88°左右时误差急剧增大。

图4 八字式转向机构优化前后的曲线关系Fig.4 Curve relationship diagram before and after optimization of the splayed steering mechanism

图5 八字式转向机构内、外转角误差曲线Fig.5 Curve of internal and external corner error of the splayed steering mechanism

3.2 转向机构力传动性能

转向机构左侧∠BCD角度变化曲线见图6，右侧∠DEG角度变化曲线见图7，左侧∠ABC角度变化曲线见图8，右侧∠EGA1角度变化曲线见图9。三角板作为八字式转向机构的原动件，绕点D右侧转动，当外转角转89°时，∠DEG为176°，说明三角板DE边与连杆EG几乎处于死点位置，∠EGA1为20°，转向机构右侧传力性能极差，∠ABC为150°，∠BCD为15°，转向机构左侧传力性能明显下降，解释了图5中内、外转角误差急剧增大的原因。

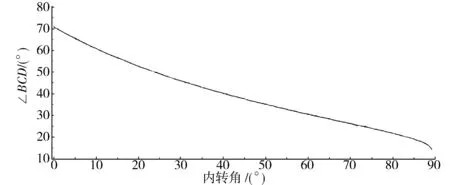
图6 八字式转向机构∠BCD曲线Fig.6 Splayed steering mechanism ∠BCD curve diagram

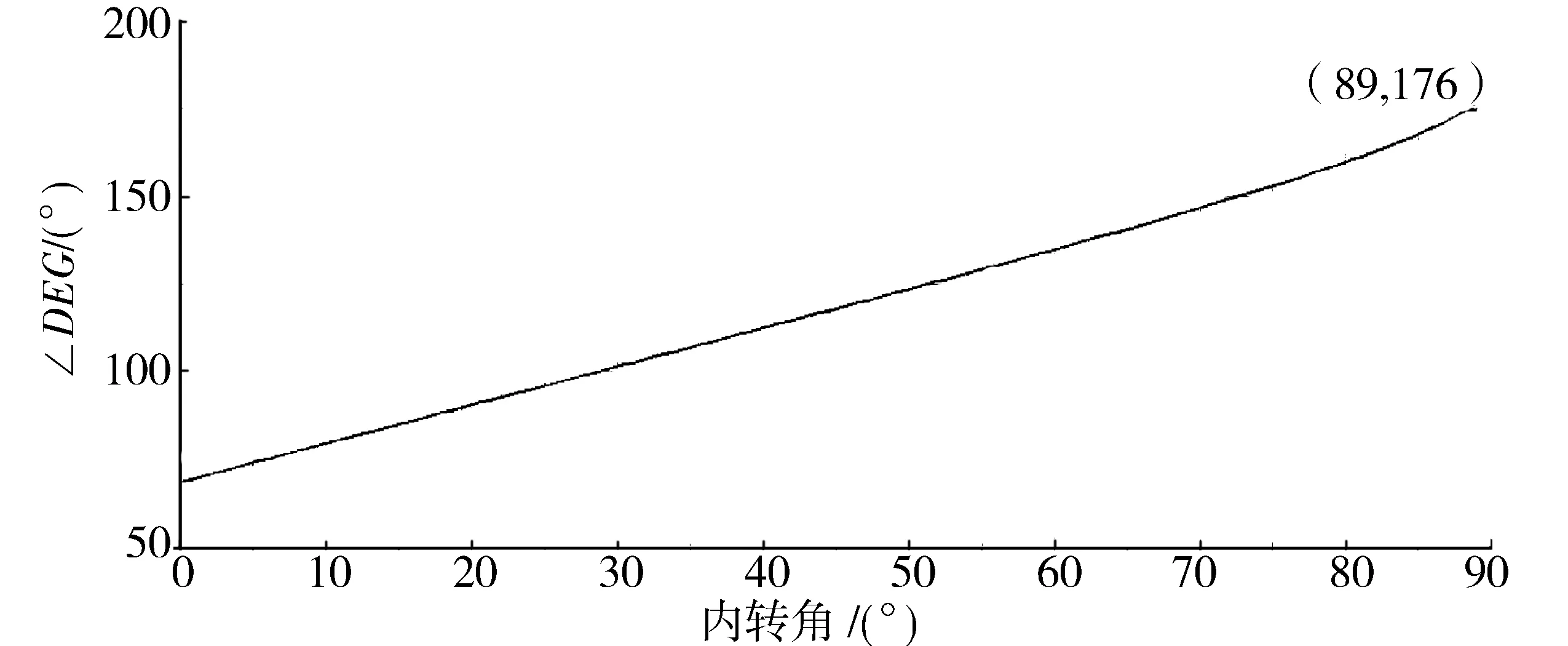
图7 八字式转向机构∠DEG曲线Fig.7 Splayed steering mechanism ∠DEG curve diagram

图8 八字式转向机构∠ABC曲线Fig.8 Splayed steering mechanism∠ABC curve diagram

图9 八字式转向机构∠EGA1曲线Fig.9 Splayed steering mechanism ∠EGA1 curve diagram

4 转向机构试验

为了评定用本方法优化后转向机构的转向性能，根据JB/T 3300—2010《平衡重式叉车整机试验方法》[10]，试制优化后样机、整车，进行最大转角及叉车转向纯滚动试验。具体测试方法[11]如下：

(1)最大转角测量方法

首先，将转向桥装配完毕，用手缓慢向左转动内轮轮毂，当内轮轮毂转动到极限位置时，用公司自制的测量角度辅助器具配合角度尺测出内、外轮轮毂在两个极限位置时，轮毂端面与两转向节主销轴线的角度，相减得到左、右转角度数。然后，用手缓慢向右转动内轮轮毂，当内轮轮毂再次转动到另一极限位置时，再次测量内、外轮轮毂在两个极限位置时轮毂端面与两转向节主销轴线的角度，相减得到左、右转角度数。

(2)叉车转向纯滚动试验

叉车呈标准无载运行状态，转向轮转到最大转角后，转向盘保持稳定，以最小稳定运行速度分别向前左、前右及后左、后右各转一圈，在转向过程中，轮胎与地面会留下痕迹，观察其与地面是否有划痕。

转向机构的转向性能检测结果见表3。测量数据与理论计算数据的最大误差为±0.5°，由此可知用本方法设计的转向机构,其转弯特性与理论仿真数据一致,证明了本方法的准确性。

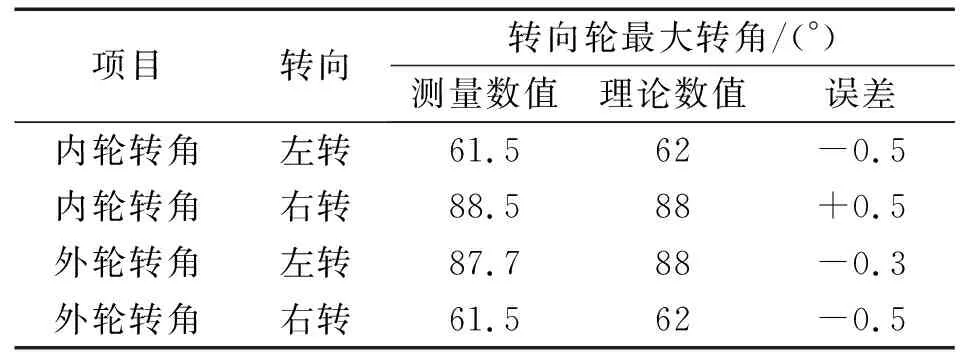
表3 转向机构的转向性能检测结果Tab.3 Test results of steering performance of steering mechanism

5 结语

本研究对八字式转向机构的工作原理及其对叉车转向性能的影响进行了分析，选取转向节节臂长度、连接杆长度、三角板铰链中心偏距、转向桥轮距、初始时转向节节臂与两车轮中心线夹角、三角板开口度、三角板边长为变量，建立了八字式转向机构的非线性优化模型，利用MATLAB软件的优化工具箱对变量进行优化，在 ADAMS软件中进行运动仿真，得到了八字式转向机构内、外轮转角关系，同时将优化前后的内、外轮转角关系与理想转向机构特性曲线相比较，发现优化后的转向机构更加接近理想特性曲线，内、外轮转角关系与理想状态极为吻合，最大转角误差不超过0.8°；对转向机构进行了力传动性能分析，在内轮转角为88°左右时误差急剧增大的原因为三角板DE边与连杆EG几乎处于死点位置，且其他连杆之间的传动角都较小。