基于薄板冲压成形的零件展开方法及其应用

胡李勇 ，王 利,2，王益平，李中华

(1.宣城职业技术学院 机电与汽车学院，安徽 宣城 242000；2.马鞍山市汽车冲压模具先进设计工程技术研究中心，安徽 马鞍山 243031；3.南京市公用事业技工学校 教务科，江苏 南京 210009；4.上海拓绅汽车电子有限公司 技术中心，上海 201213)

对坯料边界形状进行优化可以改善板料变形沿坯料分布不均匀的状况，降低应力集中和局部变薄率，提高成形极限，减少成形工序及切边余量，预防成形缺陷的出现[1-3]。坯料边界形状可以应用多种零件展开方法求解获得。零件展开一般用截面几何展开法确定坯料形状，但该方法无法适应非可展曲面，且无法关注多因素下材料的塑性变形影响。近年来，基于全量塑性理论发展起来的一步逆成形有限元法，比较合理地考虑了坯料形状展开的物理力学变形过程及其他影响因素，已成为提高拉延板料形状预示准确率的有效方法[4-6]。也有研究[7]利用增量理论有限元法来反复计算和修正坯料形状，但基于增量理论的仿真软件在目前的硬件平台上运行时间非常可观，不利于汽车覆盖件成形过程的模拟。结合增量理论有限元法，并对一般静力隐式算法改进得到的静力隐式增量法，因提高了计算精度和效率而被一些CAE软件应用[8-9]。

本研究在对零件展开方法进行分析的基础上，全面总结了零件展开的仿真应用方法与场合；以搭子件为研究对象、AutoForm软件为仿真平台，对重要的零件展开方法进行仿真与分析，以期为各类型车身覆盖件的坯料轮廓与中间工艺轮廓获取提供参考。

1 仿真数学模型

1.1 截面几何展开法理论

在三维设计软件中，一般通过中性层理论来对复杂汽车零件进行几何展开。薄板冲压成形的中性层位置确定，需要考虑以下两种情形[10]：①当成形角度θ较小、成形半径R较大时，认为板料变形程度小，中性层的位置为板料厚度中心位置；②当成形角度θ较大、成形半径R较小时，认为板料变形程度大，此时中性层向成形处的内侧移动，需要通过计算确定其位置。

1.2 一步逆成形有限元法

一步逆成形有限元法简称一步法，该方法采用Euler法，借助最终构形和初始构形的节点坐标来描述其变形过程。将虚功原理应用于最终构形可得

W=Wint-Wext=0，

(1)

式中：Wint为塑性变形能；Wext为外力所做的功。将式(1)表达成离散形式为

(2)

(3)

式中：e为单元序号；ε*为虚应变；u*为虚位移；σ为Cauchy应力；f为外力。方程(3)等效于下列方程：

(4)

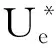
R(Ui)=Fext(Ui)-Fint(Ui)=0。

(5)

方程(5)为非线性方程，采用Newton-Raphson法求解如下：

(6)

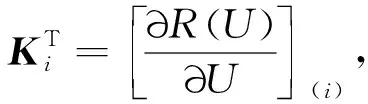
Ui+1=Ui+dU。

(7)

1.3 增量加载有限元法

增量加载有限元法简称增量法，主要分为基于全拉格朗日和更新的拉格朗日的静力隐式有限元迭代算法(SI法)、静力显式持续平衡方程法(SE法)及基于动力学中心差分格式的动力显式有限元法(DE法)。

板料冲压成形主要应用增量法分析板料的大变形非线性力学过程。可以证明，用SI法建立的有限元格式是等效的，若采用数学表达一致的本构关系，上述途径将产生同样的结果[11]。因此，经过有限元离散建立起来的坯料运动方程可表示为

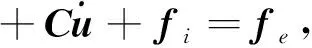
(8)

式中：M为质量矩阵；C为阻尼矩阵；u为节点位移矢量；fi为等效内力矢量；fe为等效节点力矢量。

板料成形过程是一个准静力过程，速度和加速度的影响一般可以忽略，故考虑t时刻和t+Δt时刻的平衡方程：

(9)

(10)

式(10)与式(9)相减，得到增量方程：

(11)

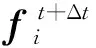
(12)

因而，得到求解方程如下：

Δu1=k-1(ut)Δfe，

(13)

u1=ut-Δu1。

(14)

当Δfe不大时，可以认为

ut+Δt=u1，

(15)

此即SE法。为了使SE法的解收敛，Δfe应尽可能小。当Δfe较大时，因为采用了式(12)，所以造成由式(14)确定的u1不满足平衡方程(11)，记此不平衡力为ΔR，则

fi(ut+Δt)-fi(u1)=ΔR。

(16)

把fi(ut+Δt)表示成u1附近仅保留线性项的Taylor展开式，得

(17)

从而，得到新的近似解：

Δu2=k-1(u1)ΔR，

(18)

u2=u1+Δu2。

(19)

重复以上步骤直至ΔR足够小，则得到t+Δt时刻的ut+Δt，此即SI法。

如果考虑式(10)包含速度与加速度在内的动态载荷力学响应，将M和C处理成对角矩阵，由DE法结合t时刻的运动方程，得到t+Δt时刻的节点位移ut+Δt，此即DE法：

(20)

各自由度的位移可以由式(20)独立求出。由于DE法条件稳定，故保证了式(20)的计算稳健性，时间步长Δt应满足

(21)

式中：Tmin为有限元系统的最小固有振动周期。

2 零件展开方法应用实例

2.1 零件展开应用场合

零件展开仿真的主要应用方法与场合总结如下：①拉延工艺平面直接展开，主要是为了粗略求解坯料轮廓[12]；②直接成形工艺有两种平面展开方式，一是利用一步法模块进行粗略展开[13]，二是利用切边线优化模块迭代反求精确展开[14-15]；③翻边面向工艺补充面有两种曲面展开方法，一是利用几何法和一步法展开或利用一步法直接展开的粗略展开，二是利用切边线优化模块迭代反求精确展开；④基于一步法的分步翻边曲面展开的多步组合应用，即后一工序作为前一工序输入的逆序展开。①和②作用相似，均可以用于拉延件或成形件的零件展开仿真，②的第二种平面展开则正常用于拉延件或成形件的零件展开仿真后期优化。上述两种方法中，②常用且重要。④是③的分步组合应用，两者的仿真过程完全相同，但目前应用③和④的公开文献较少。本方法以搭子件为对象、AutoForm软件为平台，重点研究②和③的实际应用。

2.2 零件展开应用实例

搭子件CATIA模型见图1。该零件为近似对称件，表面有多个成形处带有定位功能的冲孔，且外边界复杂并带有4处向下翻边。综上考虑，零件先成形主体部分，然后再完成向下的4处翻边，最后冲制6个圆孔。仿真时，首先应用AutoForm一步法模块算出粗略坯料边界形状，导入“igs”格式的接口文件；然后应用SI法对坯料进行成形仿真，并对比仿真零件轮廓与实际零件轮廓的误差；最后应用增量加载有限元法的切边线优化模块迭代反求出精确坯料边界轮廓，使仿真零件轮廓与实际零件轮廓之间的偏差达到两者误差的控制要求。

图1 搭子件CATIA模型Fig.1 The CATIA model of building sub parts

零件工艺设计过程(图2)及要点如下：

(1)应用一步法展开坯料，粗略获取初步仿真坯料，如图2(a)中的序号1所示，序号2为展开对象零件轮廓边界。

(2)搭子件成形工艺的重点是在成形设计时应用拉延工艺设计模具体，所设计的制件拉延模面如图2(b)所示。在翻边工艺设计过程中，翻边面向工艺补充面展开后，翻边面不能落在工艺补充面的曲面上，否则翻边后的面为曲面。图2(b)中A处的局部放大图如图2(c)所示，图中的序号3和序号4分别为几何法所得的轮廓边界和一步法展开的轮廓局部边界。经测量，序号3和序号4的最大偏差接近2 mm。

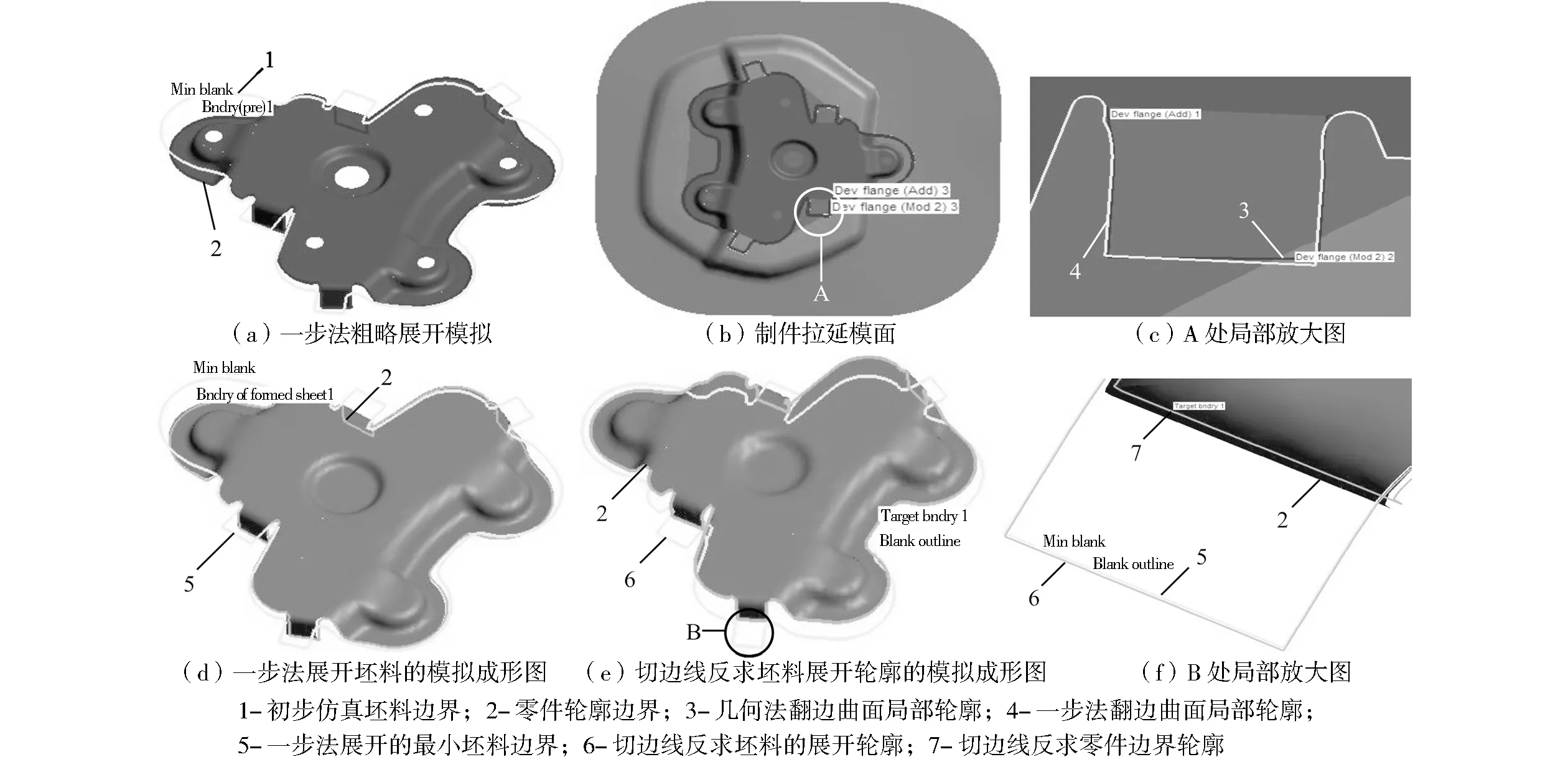
图2 零件A模型及其展开模拟Fig.2 Model of part A and its development simulation

(3)图2(d)是应用一步法展开坯料的模拟成形图，图中序号5为一步法展开的最小坯料边界。在翻边之后以零件轮廓边界为目标，应用切边线优化模块进行精确展开，结果如图2(e)所示。图2(e)中序号6为切边线反求坯料的展开轮廓。图2(f)为图2(e)中B处的局部放大图，测量图中序号5和序号6，得到最大轮廓偏差接近2 mm。图3是应用切边线优化模块，在设置边界条件为5次最大迭代次数和0.5 mm最小迭代偏差后算出的迭代反求收敛曲线，反求后的序号7切边线反求零件边界轮廓与序号2零件轮廓边界误差由原来的近2 mm缩小到了0.58 mm。因此，优化工作基本达到了设定要求。

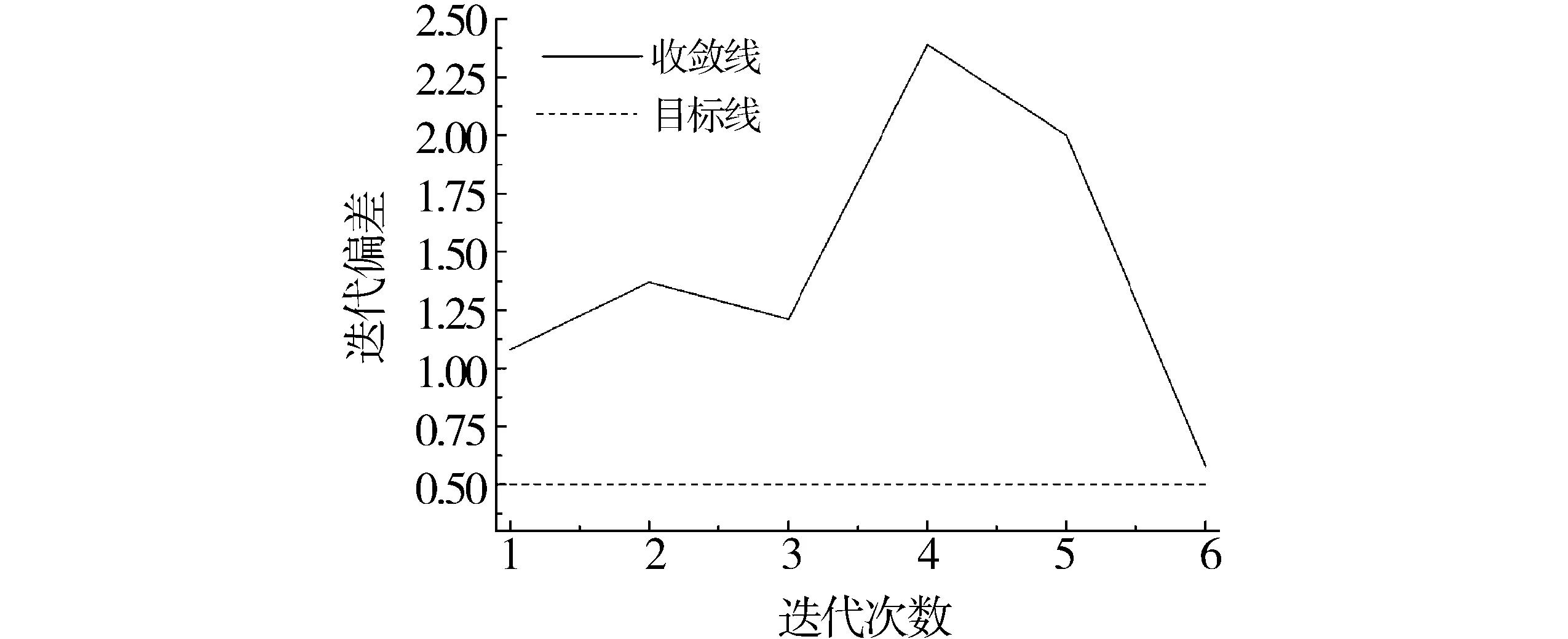
图3 切边线优化模块迭代反求Fig.3 Iterative reverse solution of trimming line optimization

3 结论

(1)应用截面几何展开法、一步逆成形有限元法和增量加载有限元法能够展开复杂制件。一步逆成形有限元法主要应用于拉延工艺平面直接展开和直接成形工艺平面展开；增量加载有限元法主要应用于利用切边线反求的精确展开。3种方法均可应用于翻边面向工艺补充面的曲面展开。

(2)在冲压成形仿真过程中，一般先应用一步逆成形有限元法粗略展开坯料轮廓，用于增量加载有限元法的仿真计算，视成形制件与零件轮廓误差，适时应用增量加载有限元法的切边线反求精确坯料轮廓，可以缩小成形制件与零件轮廓的误差。在展开精度方面，增量加载有限元法最优，一步逆成形有限元法次之，截面几何展开法最差。

(3)在制件的成形工艺设计中，研究了各类零件展开方法的应用与实际效果，对公开文献较少或重要的零件展开仿真方法进行全面分析，为各类型车身覆盖件的坯料轮廓与中间工艺轮廓获取提供了参考。