用“生长型”理念架构专题复习课的实践探索

陆红力

《义务教育数学课程标准（2011年版）》指出：“数学教学活动，特别是课堂教学应激发学生的兴趣，调动学生的积极性，引发学生的数学思考，鼓励学生的创造性思维。”这就要求我们在设计课堂活动时，要围绕知识主干寻求思维载体，设计积极的、有效的思维活动。前不久，笔者听了两节“与反比例函数有关的面积问题”的复习课，很有感触。下面以此课题为例，围绕“生长型”理念，将个人的一些思考进行阐述。

一、课题分析

1.教学目标分析。

（1）掌握反比例函数表达式中比例系数k的几何意义、反比例函数中与面积有关的基本图形以及解决与反比例函数有关的面积问题的方法。

（2）通过开放性问题的设计培养学生提出问题的能力;通过图形变式提升学生的观察能力;通过一题多解、一题多变培养学生分析问题和解决问题的能力，发展学生的合情推理的能力，渗透数形结合、化归等数学思想方法。

（3）通过对开放性问题的自主探究、合作交流，培养学生合作、创新、自觉运用数学的意识，增强学生自信心，引导学生体会数学思维的价值，促进学生个性发展。

2.教学内容分析。

本节课是苏科版数学八年级下册第11章“反比例函数”的专题复习课，属于“数与代数”的范畴，是反比例函数知识的拓展与延伸，也是后面解决函数与面积问题的基础。因此，本节课从某种意义上起到了承上启下的作用。该内容对培养学生的数学解题能力，形成数学思维方式和数学思想方法，发展学生核心素养有着重要的作用。基于以上分析，可以确定本节课的教学重点是利用反比例函数表达式中比例系数k的几何意义解决有关面积问题。

3.学情分析。

在本节课之前，学生已经学习了“与一次函数有关的面积问题”和“反比例函数”等知识，积累了一定的相关经验，有一定的联想、探究能力。但学生对于解决较复杂的图形或位置不特殊的图形的面积有一定的困难，因此，可以将解决较复杂的图形或位置不特殊的图形的面积问题确定为本节课教学难点。

4.教学方法。

本节课面向全体学生，从学生已有的知识经验出发，通过设计一系列直指问题本质的问题串，找准生长路径，从不同方向将所要复习的内容进行知识整合与创新应用。因此，课堂教学中所采用的教学方法以启发法、谈话法、讨论法、练习法为主。

二、“生长型”理念下的价值判断

“生长型”理念架构下的复习课的情怀源于生命，立意基于生长，本质体现发展，它的价值就在于尊重生命，放飞思维，收获素养。因此，教师在设计教学内容时，不仅仅是多讲几道题，让学生多做几道练习，而是要更多地考虑学生的主动参与、自主探究、情感向往，要以学生的发展为目的。教师可以选取与教学内容相近或相邻的知识，选准一条复习的主干，采用“变式图形”的生长路径，用这一新视角将教学内容有机融合、整体构建;可以选择动态性材料，引导学生从思考静态问题转向动态问题，发散学生的思维;还可以设计开放性问题，让学生结合自己的知识经验编制不同的问题，提高学生的积极性，激发学习兴趣，同时也能培养学生的创造能力，让学生在学习过程中又一次成长。

三、价值判断下的活动设计

活动1：模型建构。

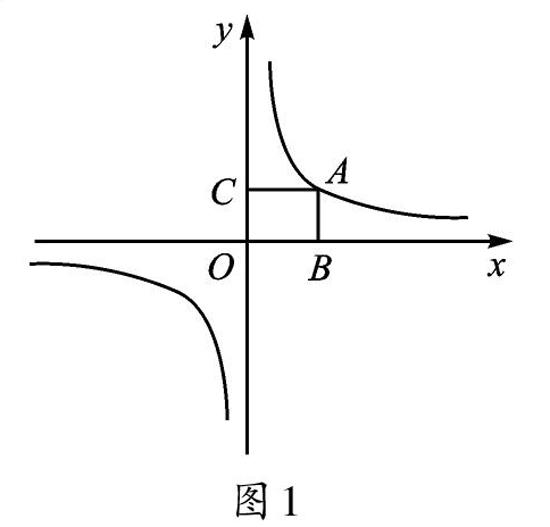
问题1：如图1，点A在反比例函数y=[2x]的图像上且橫坐标为2，过点A作x轴、y轴的垂线分别交x轴、y轴于点B、点C，求矩形ABOC的面积。

设计意图：复习反比例函数图像上的点坐标的求法和用坐标求矩形面积的方法，为本节课的探究教学提供了基础和有效的教学资源。

预设生成：这是本节课的起点，起点很低，绝大部分学生都能解答。

问题2：在问题1的条件下，将“点A的横坐标为2”改为“点A在反比例函数y=2/x的图像上运动”，你还能求出矩形ABOC的面积吗？

设计意图：由静态到动态，由特殊到一般，体会用字母代替数值的方法，感受解题方法与结论的不变性。

预设生成：如果学生说，设点A的坐标为（x，y），则AC=x，AB=y，则SABOC=xy=2。教师可追问：“若点A在第三象限呢？”让学生在自我反省中领悟坐标与线段长度的区别，及时纠正，再总结出对于反比例函数y=k/x（k≠0），点A是反比例函数图像上的任意一点，矩形ABOC的面积始终为IkI。

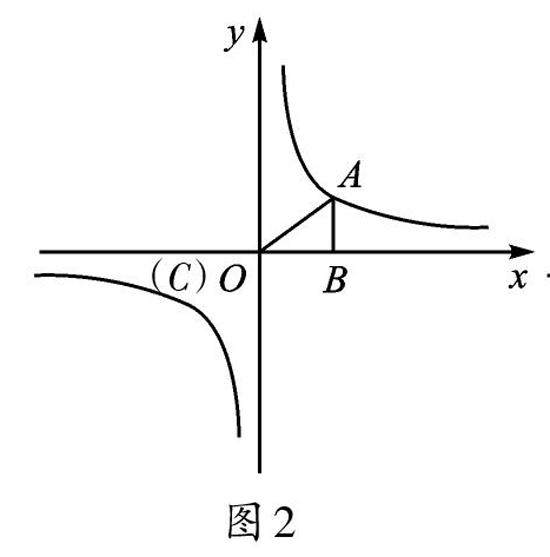
问题3：如图2，在问题2的条件下，若将点C移动到坐标原点O，求此时△ABC的面积。

设计意图：通过对图形进行特殊化处理，形成如图2所示的三角形，此类三角形也是反比例函数中常见的具有面积不变性的图形。以上问题的设计，一方面是让学生了解图形的变式过程，另一方面是加深学生对这个特殊图形的认识。学生不但要认识它的特殊性，还要认识它的用处。教师教学时可与问题1中的矩形一起作为基本图形。

预设生成：在问题2的基础上，学生不难发现，此时△ABO的面积为矩形ABOC面积的一半，即S△ABO=k/2。

活动2：模型应用。

问题4：如图3，若点C在y轴上继续运动，△ABC的面积会发生改变吗？

设计意图：图形由静态向动态发展，更利于揭示问题的本质，让学生体会特殊到一般的转化，感受图形与图形之间的神奇变化，激发学生学习的积极性。

预设生成：当点C在y轴上运动时，此时△ABC的底AB与AB边上的高都保持不变，所以△ABC的面积保持不变，始终与△ABO的面积相等，为IkI/2。若学生没有发现△ABC和△ABO面积的关系，也可以引导学生利用坐标法求解。

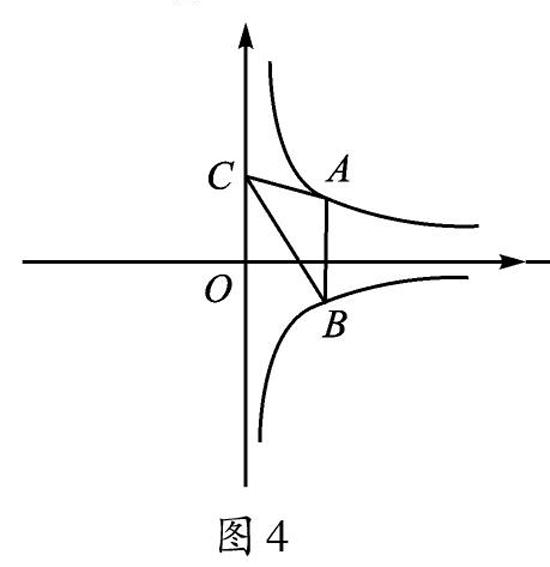
问题5：如图4，若将问题4中“点B在x轴上”，改为“点B在反比例函数y=-1/x（x>0）的图像上”，其他条件不变，求此时△ABC的面积。

设计意图：随着点B位置的变化，图形也发生了改变，但是转化为基本图形的思想方法不变，此设计进一步提升学生的化归能力。

预设生成：如果有学生从坐标的角度去解决问题，教师首先要肯定学生的做法，并提出坐标法是解决此类面积问题的万能方法，再引导学生从整体性的角度去寻找几何解法。如图5，将△ABC的面积先转化为△ABO的面积，且△ABO的面积为△AOD与△BOD的面积之和，再利用基本图形可得△AOD的面积为1，△BOD的面积为1/2，所以△ABC的面积为3/2。

问题6：请同学们再改变点B的位置，提出一个与面积有关的问题。

设计意图：设计开放性问题，把所要研究的图形串联起来，一方面省时省力，另一方面培养学生发现问题、提出问题、分析问题、解决问题的能力。

预设生成：这个环节，要给予学生足够的时间，让学生创造性地重新设计问题，感受学生的智慧，体会意外的惊喜。学生可能会产生如下想法。

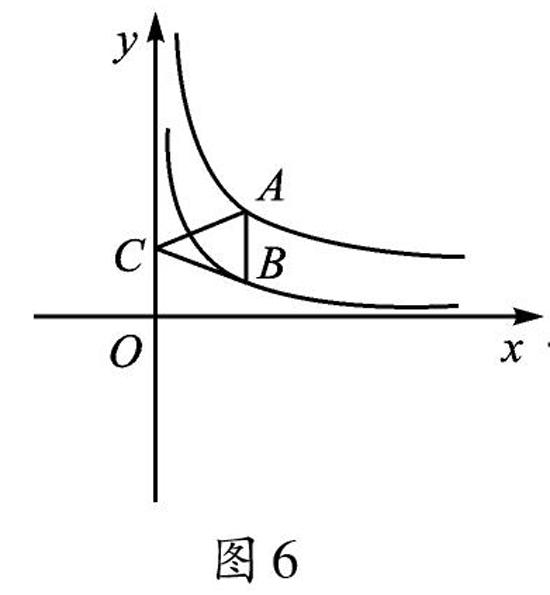
想法1：如图6，若把点B移到反比例函数y=1/x（x>0）的图像上，求△ABC的面积。

想法2：如图7，将问题3中的“AB⊥x轴”换成“△AOB为等腰三角形”，求△ABC的面积。

活动3：拓展延伸。

若点B也移到反比例函数y=2/x的图像上，设置以下问题。

问题7：如图8，若点A（1，y1）、点B（2，y2）在反比例函数y=k/x（k>0）的图像上，且△AOB的面积为3，求k的值。

设计意图：这是一道与反比例函数有关的面积问题的逆向问题，通过综合运用割补法以及利用反比例函数中的基本图形的面积公式求图形面积的方法，一题多解，培养了学生的求异思维。

预设生成：学生可能会有以下几种不同的解法。如果方法不全，教师可设计问题引导。解题结束后总结归纳，揭示方法，引导学生根据图形的结构对图形进行拆分，找到基本图形，让学生整体上掌握解决这些问题的策略。

生1：如图9，过点A、点B分别作AC⊥x轴，BD⊥x轴，垂足分别为点C、点D。因为SOABD=S△AOC+SABDC=S△AOB+S△BOD，又因为S△AOC=S△BOD，所以S△AOB=SABDC=1/2（k/2+k）=3，解得k=4。

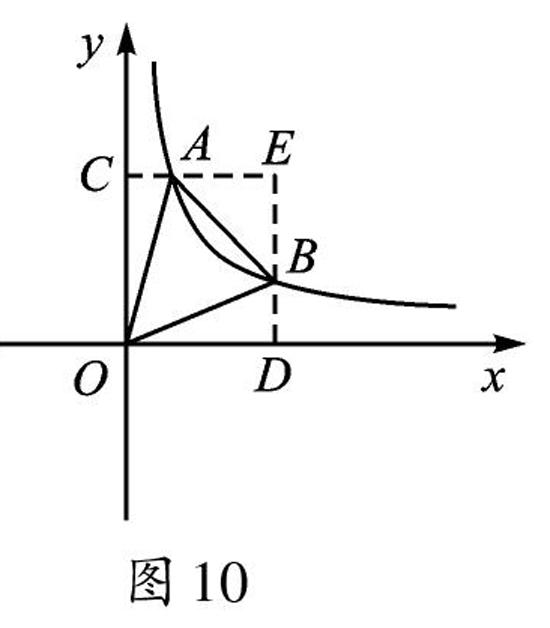
生2：如图10，过点A、点B分别作AC⊥y轴，BD⊥x轴，垂足分别为点C、点D，延长CA、DB交于点E。S△AOB=SODEC-S△AOC-S△BOD-S△ABE=2/k-k/2-k/2-1/2·k/2·1=3，解得k=4。

学生在解决问题后，教师要加以引导，归纳解法，揭示本质。

四、活动设计下的教学思考

1.把握数学教学价值。

数学学习是一个不断实践的过程，在课堂实践过程中，对学生开展有价值的教学活动应该是这样的：学生在实践中不断形成并积累发现问题、提出问题、分析问题、解决问题的能力和经验。对于“生长型”理念架构下的复习课，教师应在相近或相邻的知识衔接点、生长点上开展数学教学活动，不断让学生在活动中积累经验，以此来增强学生观察事物、探究规律和解决问题的能力。

本节课所承载的教学价值绝不是让学生完成各种情境下与反比例函数有关的面积问题的解答。教师不应在学生面前呈现静态的情境，让学生在一系列不同的情境中茫然且机械地完成解答。因此，本课例创设有效的教学情境，将特殊点变为一般点，让定点变为动点，通过一系列的变式图形引出新问题，让学生面对问题自然地做出选择，不断地优化自己的想法与做法，在思维过程中积累经验，增长智慧，实现教学价值。

2.凸显数学核心素养。

数学素养是人们通过自身的实践和认知活动所获得的数学基础知识、基本技能、数学思想和观念，以及由此形成的数学品质和解决问题能力的总和。生长理念不仅仅在于让学生获得一些数学知识和技能，更在于让学生通过领悟数学本身蕴含的智力价值和精神价值，提升数学素养，因此，开展“生长型”理念架构下的复习课教学是提升数学核心素养的有力抓手。

本课例中，教师要关注并挖掘教学资源，不断改变认识的对象，让学生观察这些图形的特征，研究图形的结构，从宏观到微观、从整体到局部，来认识基本图形的本质属性。教师适时进行方法性指导，通过整体转化或割补转化，提升学生的观察力。课例中设计的开放性问题，培养了学生提出问题的能力、自觉运用数学知识的意识与能力以及创新意识。这些都是提升数学核心素养的重要手段。

3.关注学生生命发展。

用“生长型”理念架构复习课的教学，是关注人的生命成长的过程，是将知识生长与人的生命成长协同发展的教学理念的具体体现，也是彰显个性发展的过程，更是体悟知识生长、生命成长的过程。

本课例从知识体系和知识结构上把握與反比例函数有关的面积问题的教学内容和教学要求，选准问题的起点与终点，通过变式图形凸显生长过程，让这些常见又有用的图形，没有遗憾地、全景式地暴露在学生的视野中。更重要的是，这些变式图形是学生通过强化条件或弱化条件得来的，这是更高层次的思维方法，是无法通过解决一两道习题所能达到的。这样的教育是促进学生全面成长、个性成长的过程，是教育的终极目标。