基于JRC-JMC模型岩质边坡稳定性及可靠度分析

高诗钦，孙树林*，吴孙星，张 岩，李思远

(1.河海大学地球科学与工程学院，南京 210098； 2.河海大学岩土力学与堤坝工程教育部重点实验室，南京 210098)

0 引言

岩质边坡稳定性分析是工程防灾减灾的重要研究领域，其内部存在大量不连续面如节理、裂隙等，这些结构面不仅对岩体的变形破坏起控制作用，且其抗剪强度特性也与边坡稳定性密切相关[1]。现有的稳定性分析大多基于Mohr-Coulomb线性强度准则，然而Barton等[2-3]通过大量节理直剪试验发现结构面上的抗剪性能并不总是满足该准则，尤其在低正应力条件下，其得出的抗剪强度明显偏大，为此提出了用于估计不规则、无充填结构面峰值抗剪强度的非线性JRC-JCS经验公式，尽管已有研究基于非线性准则对岩质边坡稳定性进行评判[4-6]，但大多没有考虑地震作用或仅限于拟静力法的范畴而忽略了地震力随时间动态变化的特性；同时忽略了实际工程中地震作用及结构面参数等影响边坡稳定的各种因素的不确定性，也具有一定的局限性。

针对以上问题，基于JRC-JMC模型，利用改进拟动力法，考虑地震作用随时间的动态特性，同时考虑锚固效应推导出边坡稳定性安全系数，分析各参数对边坡稳定性的影响：在确定性计算模型的基础上，考虑地震作用及结构面参数的变异性，建立了岩质边坡抗滑稳定性的可靠度模型，分析各参数均值及变异系数对可靠度指标β的影响。

1 理论推导

1.1 JRC-JMC模型

Barton[2]等基于大量人工拉断结构面的直剪试验结果，提出了用于估计不规则、无充填结构面峰值抗剪强度的非线性JRC-JCS经验公式：

τ=σntan[φb+JRClog(JCS/σn)]

(1)

式中:τ为抗剪强度，MPa；σn为法向正应力，MPa；φb为岩石基本内摩擦角，一般取值29°；JRC为结构面粗糙度系数；JCS为结构面岩壁强度，MPa。

赵坚[6]在Barton非线性准则基础上考虑节理吻合度系数JMC得到改进的JRC-JCS模型，其表述为：

τ=σntan[φb+JMC·JRClog(JCS/σn)]

(2)

JMC取值为0.3～1.0，当JMC为1.0时即简化为Barton准则。在实际工程应用中，常常将该准则下各抗剪强度参数等效转化为线性Mohr-Coulomb准则下强度参数，表述如下：

τ=c+σntanφ

(3)

其中设f=tan[JRC·JMC·log(JCS/σn)+φb]

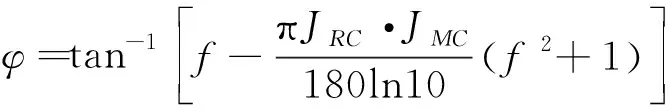
式中：τ为抗剪强度，MPa；f摩擦系数；c为黏聚力，MPa；φ为内摩擦角，(°)。

1.2 改进拟动力法

传统拟动力法仅考虑入射波在整个线弹性介质中向上传播，从而违反了自由表面零应力边界条件[7]，为弥补传统拟动力法的不足，考虑地震波传播介质的黏弹性，假设岩质边坡为Kelvin-Voigt黏弹性介质材料[7]，岩质边坡的横波波速为Vs，纵波波速为Vp，Bellezza[8]等提出了一种改进的拟动力法，该方法中针对地震加速度随边坡高度变化仅体现在CSZ、SSZ、CPZ、SPZ等参数中，但实际计算过程中发现地震加速度值随高度变化影响较小，很难完全体现出岩质边坡中相邻结构几何形状和刚度、岩体刚度和阻尼、岩体深度等因素综合产生的放大效应，结合传统拟动力法特点，故再次引入放大系数fs，根据Bellezza[8]等研究可知在岩体任意深度z处，任意时间t时地震作用下考虑放大系数后水平和垂直地震加速度：

(4)

(5)

CS=cos(ys1)cosh(ys2)

SS=-sin(ys1)sinh(ys2)

CP=cos(yp1)cosh(yp2)

SP=-sin(yp1)sinh(yp2)

式中：Vs为岩质边坡的横波波速，m/s,VP为岩质边坡的纵波波速，m/s；G为岩体剪切模量，MPa；ρ为密度，kg/m3；υ为泊松比；kh、kv分别为水平与竖向地震系数；fs为地震放大系数；g为重力加速度，m/s2；ω，(°)；T为地震振动周期，s；D为岩石阻尼比；H为边坡高度，m。

1.3 计算模型与公式推导

图1为典型锚固岩质边坡几何要素剖面图，张裂缝在坡顶为垂直向深度为h，H为坡高，滑裂面倾角α，坡角β，张裂缝距坡顶缘的水平距离为LAB，滑裂面长度为LOC，TT为锚索拉力，kN，θ为锚索拉力与水平面夹角，(°)。

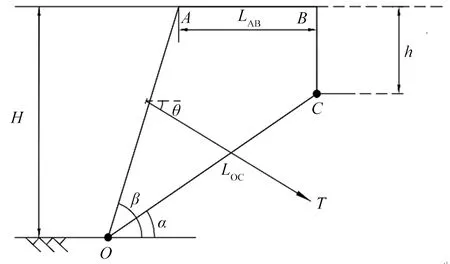
图1 典型岩质边坡几何要素Figure 1 Typical rocky slope geometric essential factors

通过图1几何关系可知滑移体OABC的面积：

(6)

由此可知破坏体自身重力W。

(7)

式中：γ为岩石容重，kN/m3。

任意深度z处水平微分单元体的质量：

(8)

由此得出整个破坏体所受水平及竖向地震力大小：

(9)

(10)

考虑锚索拉力TT，可得出滑裂面上的正应力σn:

(11)

由JRC-JMC强度参数等效为Mohr-Coulomb准则下强度参数可知滑裂面上抵抗岩质边坡滑动的力Fr:

Fr=τ·LOC=(c+σntanφ)·LOC

(12)

将式(3)～(10)代入式(11)可知：

(13)

滑裂面上促使破坏体下滑的力Fi：

Fi=(W+Qv)sinα-Qhcosα-TTsin(α+θ)

(14)

由此得出岩质边坡抗滑稳定安全系数Fs：

Fs=Fr/Fi

(15)

式中参数同上文。

2 算例及参数分析

以图1所示岩质边坡经典模型为例，为研究各影响因素对其稳定性的影响，基本参数取值如下：岩石阻尼比D=0.3、地震周期T=0.3s、Vs=2 900m/s、Vp=3 900m/s，假设kh为0.3，kv为0.15，结构面参数JRC=10、JMC=1.0、JCS=50MPa下，锚固力TT为100kN，夹角为20°，边坡H为10m,β为60°,α为30°，h为2m，研究某一变量变化时，其他变量取值如上。

2.1 锚固效应的影响

考虑锚固效应时，固定锚固角度为20°时，研究锚固力TT在0～400kN、θ在0°～90°时对Fs的影响，结果如图2(a)、图2(b)所示。

由图2可知，Fs随TT增大而增大，当TT由0增大到400kN，Fs提高了82.41%；Fs随θ增大而减小，θ由0°增大到90°，Fs降低了9.62%，且Fs最大值出现在15°～30°，与实际工程相符。

2.2 地震作用的影响

为分析地震作用对边坡稳定性的影响，设kh为0～0.4，kv为-0.2～0.2(Qv方向向下为正，向上为负)，fs=1.0～1.8时，其他参数不变进行分析，同时研究对破坏面上等效强度参数c、φ的影响。

2.2.1 水平地震系数的影响

如图2(c)所示，保持kv为0.1，Fs随kh增大而降低，在fs从1.0增大到1.8时，Fs降低了57.06%、61.34%、65.21%、68.74%、71.98%。由此可知，kh对Fs影响显著，fs的影响也不可忽略，边坡稳定性评判时仅用拟静力法是不够精确的。图3(a)展示了kh对滑动面c、φ的影响，等效黏聚力c随kh增大而减少，等效内摩擦角φ则相反，由于水平地震力提供的是下滑力分量及减少滑裂面上法向正应力的作用，抗剪强度随kh增加逐渐减小的，可知c的下降比起φ增加对边坡稳定性影响更加显著。

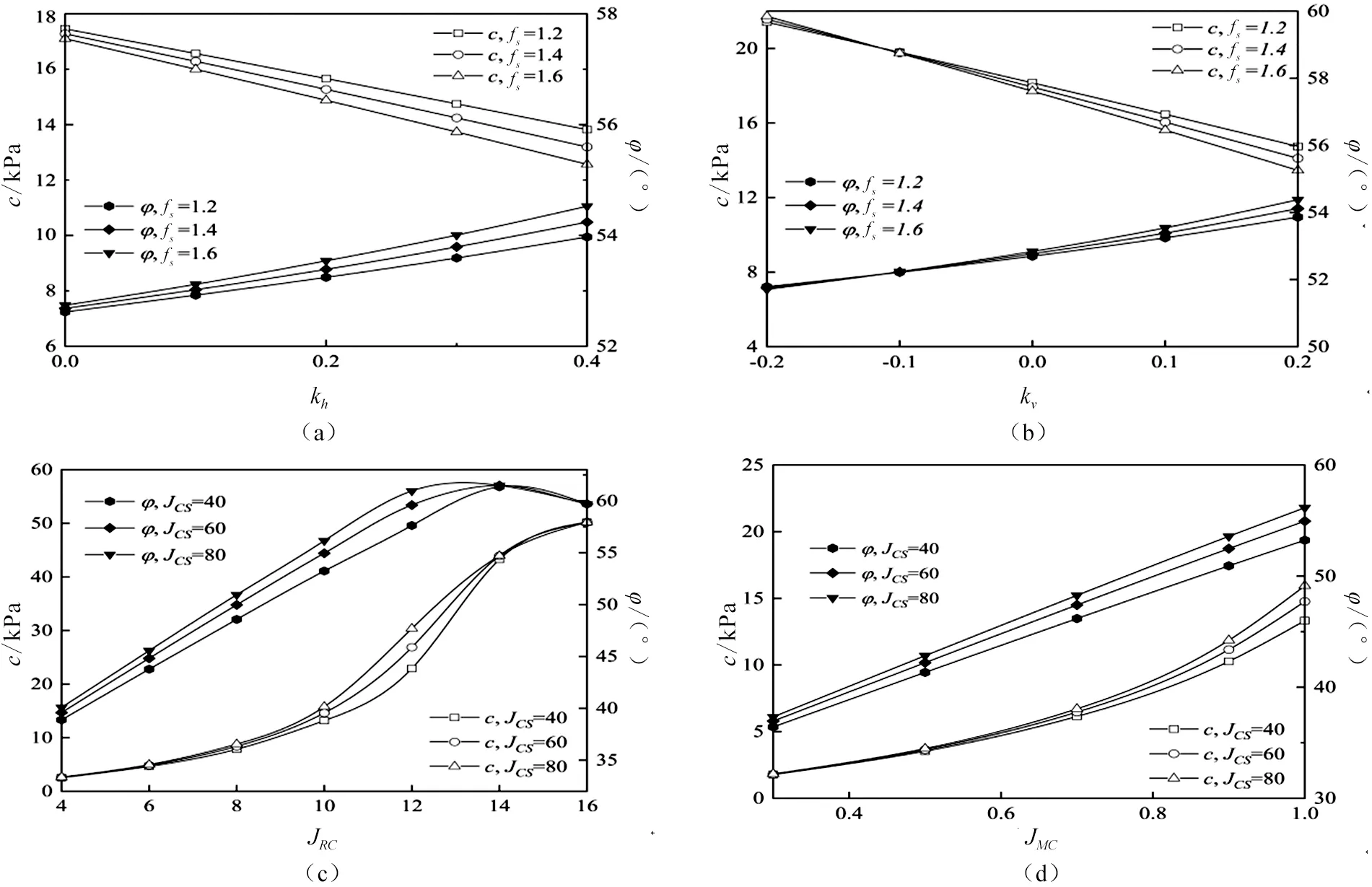
图3 对c和φ的影响Figure 3 Impact on c and φ

2.2.2 竖向地震系数的影响

考虑kv对边坡稳定性的影响，kh为0.2不变，由图2(d)可知，安全系数Fs随kv的增加呈现缓慢降低的趋势，且在fs=1.0～1.8五个等级下分别降低了3.24%、5.58%、8.28%、11.32%、14.67%。相比于kh，kv对Fs的影响较小，且考虑竖向地震力的影响时，fs比kv对Fs的影响更加显著。由图3(b)可知，c随kv和fs变化趋势与Fs一致，但此时fs对c的影响远没有kv的影响显著。此外，φ不管随kv还是fs的变化都较小，其幅度保持在2°左右。

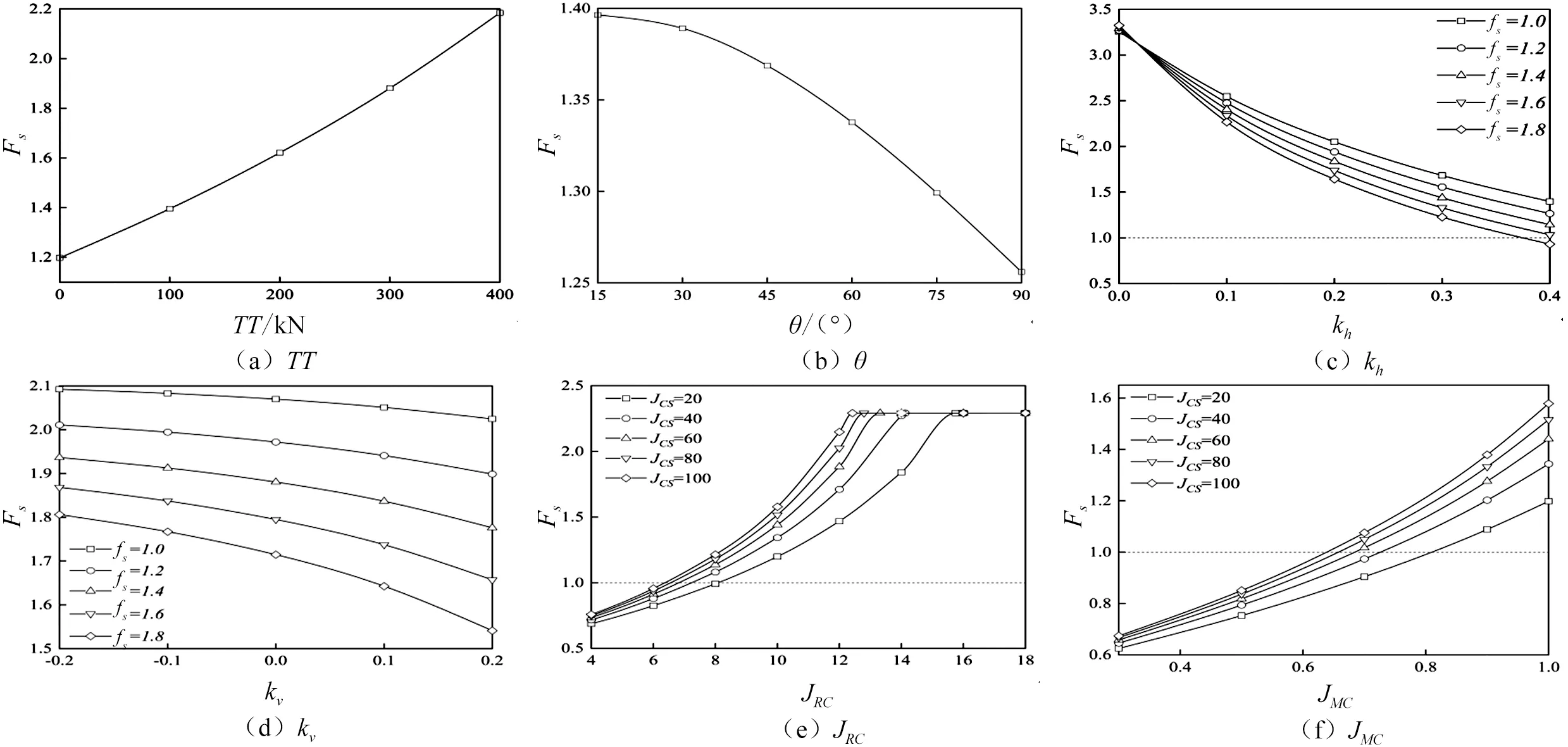
图2 对安全系数的影响Figure 2 Impact on safety factor

2.3 结构面参数的影响

为分析结构面各参数的影响，其他条件不变，重点考虑结构面的岩壁强度JCS在0～100MPa、结构面粗糙程度系数JRC为4～16及节理吻合系数JMC在0.3～1.0时对Fs的影响。

2.3.1 结构面粗糙度系数的影响

保持JMC为1.0时，分析JRC在4～16时对边坡稳定性的影响。由图2(e)可知，Fs随JRC的增大快速增大，当JRC较小时，Fs甚至远小于1.0，当JRC增大到8之后，Fs出现急剧增加，但当JRC增加到一定数值后，不同JCS下Fs保持不变。事实上在实际工程中，公式(2)中φb+JMC·JRC·lg(JCS/σn)不应大于70°[5]，若超过70°则以70°值计算，使得Fs的值随JRC和JCS增长始终保持不变，这也说明法向应力σn不可能无限小而存在最小值。

同样的，如图3(c)所示，随着JRC及JCS的增加，等效强度参数c、φ都呈现增大的趋势，随着JRC值的增大，c的增长速率趋于平缓且JCS的增长几乎对c无影响。

综上可知，JCS和JRC的变化对Fs有显著影响，且JRC影响程度相对更大。

2.3.2 结构面吻合程度系数的影响

保持JRC为10时分析JMC在0.3～1.0时对Fs的影响。如图2(f)所示，Fs与JMC呈正相关，当JMC较低时，Fs远不能达到工程建设的标准，随着JMC的不断增大到1.0，不同JCS下Fs分别提升了91.7%、108.05%、118.87%、127.24%、134.17%，可见JMC的影响更加显著。

图3(d)给出了随JMC增大时c和φ的变化，可知二者都与JMC呈正相关，与Fs变化相似的是，低JMC时c和φ变化幅度都较小，随着JMC逐渐增大，c和φ都出现了明显的提升。

综上可知，低JMC和高JMC情况下无论是Fs还是c和φ大小都相差悬殊，且其他参数如JRC、JCS等在低JMC值下对边坡稳定性起的作用影响较低。因此，实际工程中应谨慎合理的考虑JMC的取值。

3 可靠度分析

岩质边坡稳定性分析时地震作用及结构面参数具有一定的不确定性，而传统确定性分析方法采用平均参数值进行计算无法准确反映岩体属性的不确定性[9-10]。为此本文基于蒙特卡洛(Monte Carlo)法对地震作用下岩质边坡的稳定性进行可靠度分析，根据可靠度基本理论及边坡稳定性的决定因素，可建立边坡稳定性极限状态方程：

Z=g(x1,x2,x3,…,xm)-1

(16)

式中：x1,x2,x3,…,xm为影响边坡稳定性的各不确定因素且具有一定分布状态的独立随机变量；g(x1,x2,x3,…,xm)为利用蒙特卡洛方法产生符合各随机变量概率分布的一组随机数代入由式(13)～(15)中得出的安全系数Fs，由此可以求出Z值。

当通过Monte Carlo法抽取N组数据便可得到N个相对独立的样本值Z，定义Z<0为边坡发生失稳破坏事件[11]，统计N次试验中出现的失稳次数M，当试验次数N足够大时，即可得出Monte Carlo法下的失效概率Pf：

Pf(Z<0)=M/N

(17)

由此可得出可靠度指标β

β=1-Φ-1(Pf)

(18)

式中：Φ-1为标准正态累积概率分布反函数。

影响岩质边坡稳定性的各因素中，边坡几何要素及锚固的变异性可忽略不计，故假定边坡高度H、张裂缝深度h、坡角β、滑裂面倾角α、岩石容重γ、锚固力TT和锚固角θ为常量，且分别为10m、2m、60°、30°、25kN/m3、100kN、20°，而地震作用下各参数kh、kv、fs，结构面参数JRC、JMC、JCS都有一定的变异性[11]，其分布状态如表1所示。最后，利用Monte Carlo法使用数学分析软件抽样进行N=100 000次时，进行边坡稳定性可靠度分析(表1)。

表1 可靠度分析计算参数

3.1 地震作用对可靠度指标的影响

保持JRC均值为8、变异系数为0.1；JMC均值为0.7、变异系数为0.1；JCS均值为40、变异系数0.2不变的情况下，分别研究kh、kv、fs均值μ和变异系数(COV)对β的影响，结果如图4所示。

由图4可知，β随着kh、kv、fs均值μ的增大都呈减小的趋势。可见，kh对边坡稳定性可靠度影响最显著，fs次之而kv影响相对最低，这与确定性分析时对Fs影响时一致。

由图4可知，相对均值μ的变化来说，三者变异系数变化对β影响都较低，特别是kv变异系数的影响几乎可忽略不计。当kh、fs均值较大时，随着变异系数的增大β反而略微增加，这表明均值较大时，若变异系数较小，通过Monte Carlo法取随机数时产生的数据大多在均值附近且变化幅度较小，而随着参数变异系数的增大，取值的幅度也相对变大，导致出现曲线中参数均值较大时随变异系数增大可靠度β也增大的现象。

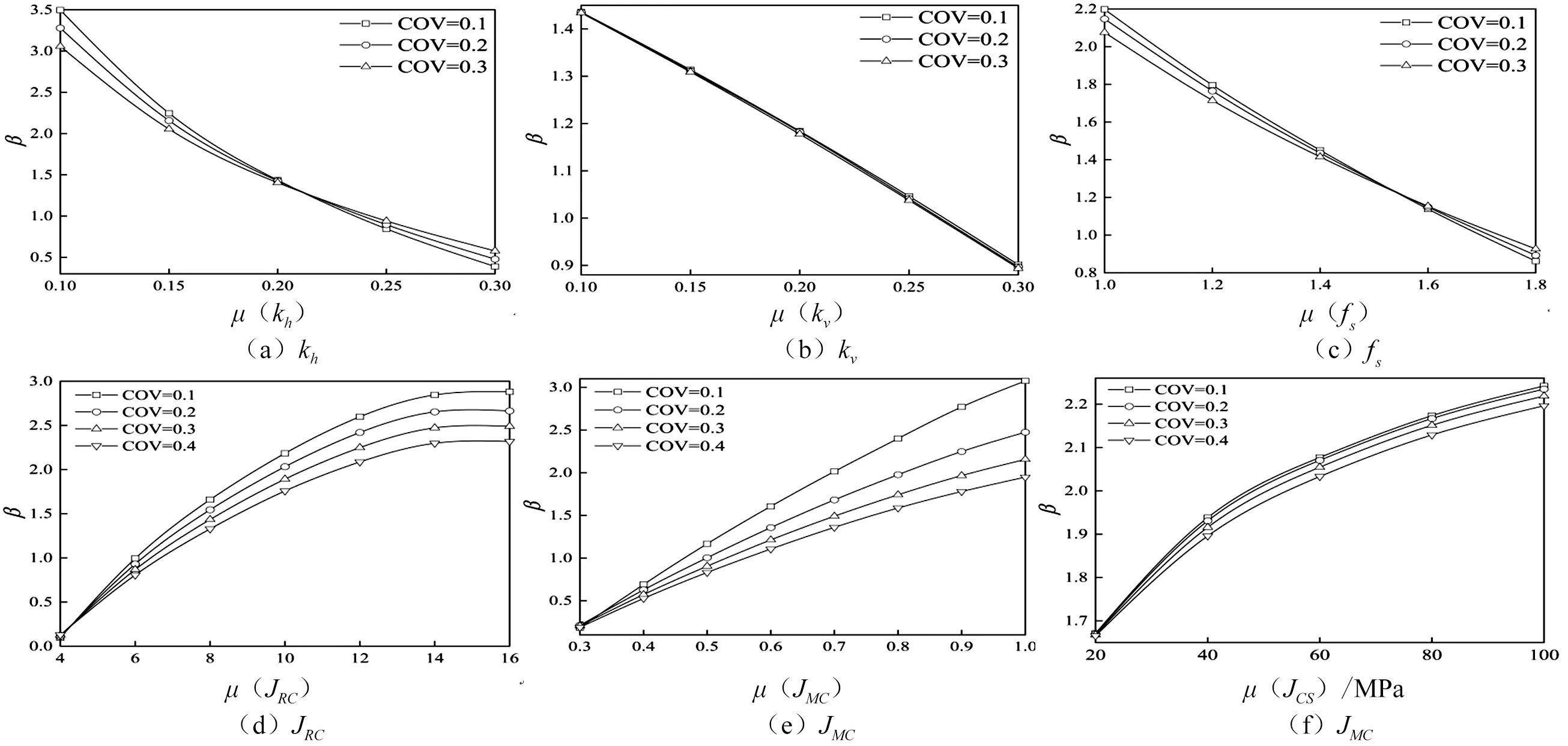
图4 对可靠度指标β的影响因素Figure 4 Impact factor on reliability index β

3.2 结构面参数对可靠度指标的影响

考虑JRC、JMC、JCS对可靠度β的影响时，保持kh均值0.2、变异系数为0.1；实际上kv值在确定性分析Fs时可正可负，故取kv均值为0.0、变异系数为0.1；fs均值为1.4、变异系数为0.2不变时，且单独分析一参数时保持其他参数均值及变异系数不变，分别研究JRC、JMC、JCS均值及变异系数对β的影响，结果如图4所示。

由图4可知，β随JRC均值μ增大出现显著的增加，当JRC由4变化到16时，不同变异系数下β大小增加了2.58～2.75；JMC均值由0.3增大到1.0，不同变异系数下β数值增加了1.76～2.89，且这种趋势随变异系数增大而减少；JCS均值由20变化到100MPa时，不同变异系数下β数值大致都增加了0.57。可见，JRC和JMC对β影响程度明显大于JCS，这与公式(2)中JRC-JMC模型准则中体现出的结构面各参数的相关度表现一致。由图4(d)可见，当JRC较大时，β随均值增加而逐渐平缓，这与公式JRC·JMC·log(JCS/σn)+φb不能大于70°有关，而随着JMC均值的不断增加，β近乎呈现线性增加，JCS均值增大到40MPa后，β随JCS均值增加也表现出相似的线性增加趋势。

由图4可知，β随着各参数变异系数增大而减小，三者对β的影响远小于均值的影响，相似的是JRC及JMC变异性变化对β更为显著，尤其JMC变异性的变化，而JCS变异系数的变化对β的影响较低，这同样印证了JCS对边坡可靠度影响较其他参数影响更低，也同样表明实际工程中针对JRC和JMC的取值应尽量合理规范。

4 结论

根据JRC-JMC模型及改进拟动力方法，在确定性模型和不确定性模型基础上对岩质边坡稳定性影响因素进行分析，得到如下结论：

1)考虑节理吻合系数JMC的影响，克服了B-B 准则过高估计天然节理剪切强度的不足，改进拟动力法中地震放大系数fs的影响不可忽略。

2)随着地震加速度系数kh、kv和地震放大系数fs的增大，边坡稳定安全系数逐渐减小，且可靠度指标β随三者均值的变化趋势与安全系数一致，更加证明了可靠度方法的适用性。

3)结构面参数显著影响着岩质边坡稳定性，随着结构面参数JRC、JMC、JCS不断增大，安全系数呈现非线性增长，且JRC和JMC取值对边坡稳定性尤其重要；可靠度指标β同样随着各参数均值的增加而增大，且三者变异系数的变化对β的影响也不容忽视。

4)通过确定性分析法得出安全系数和不确定性分析法得出可靠度指标同时评估岩质边坡的稳定性，更有利于为边坡抗震安全设计提供理论指导。