昆明呈贡地区重塑红土动力特性研究

李 帆，郑家毓，符必昌

(昆明理工大学国土资源工程学院，昆明 650032)

0 引言

红土广泛分布于我国云贵地区、两广地区以及湖南、福建等多个省份[1-2]。红土的工程地质特性十分复杂，与一般土相比，红土具有较高的含水率、孔隙比以及低密度和较高的强度，因此红土既有软土的性质同时又表现有砂质粉土的特点[3-4]。由于形成红土的条件特殊，红土种类多样，不同气候条件以及地质环境的差异使得不同地区的红土表现出的物理力学特性差别较大，从而导致相关的红土研究结果通用性不强。因此对该地区重塑红土动力特性进行研究对于指导该地区的工程经济建设以及抗震设计具有实际意义。

1 动三轴试验方案设计

1.1 试验土样及制备

本文试验土样取自昆明呈贡地区某工程建设场地，试验起止时间为2020年9月16日至10月11日，试验地点为昆明理工大学岩土工程实验室；依据《土工试验方法标准》[5]测得其基本物理指标如表1所示。试验采用重塑土样，控制土样干密度为最大干密度，采用击实法对土样分3层击实，同时为保证制成的试样均匀不出现分层情况，每层击实后对交界面进行刮毛处理，制成h=80mm，φ=39.1mm的圆柱体试样，随后将制好的试样进行真空抽气饱和。

表1 昆明呈贡地区红土基本物理指标

1.2 试验方案

本次试验为固结不排水试验，动荷载为频率为1Hz的正弦波。先对试样施加不同固结围压，待试样固结变形稳定后，将动应力幅值由小至大分为若干级进行加载，每级循环加载次数为10次；试验共制备12个试样(其中3个作为备用)，3个试样为一组，共分为3组，分别在不同围压下使各组试样固结，同时将固结比控制为不同大小，试验终止条件为轴向变形达5%。

2 试验结果及分析

2.1 骨干曲线

根据动三轴试验结果取每级荷载的第5个循环加载周期数据进行处理，绘制其骨干曲线如图1所示。由图1可知红土的动应力-应变呈现出明显的非线性关系。根据曲线形态可将红土的动应力-应变发展过程分成三个阶段：在试验初期，由于对试样施加的动应力较小，此时土体的结构保持的相对较为完整，土体内的土颗粒在动荷载作用下被挤压产生垂直位移，从而土颗粒被挤压密实，该阶段土体的变形呈现出近似弹性变形，其动应力-应变曲线大致呈一条直线；在试验中期，随着所施加的动应力增大，曲线相对于初期时斜率变小，对试验施加的动应力变化不大，而其动应变却发展迅速，土样开始出现塑性变形；在试验后期，继续增大动应力，此时土体的变形增加迅速，土体强度突然下降标志土体发生失稳破坏。除此之外，对试样施加的固结围压越大曲线越高，即要使土体达到相同的动应变，需要对土体施加更大的动应力，这是因为对试样施加固结压力会增大土体中土颗粒的咬合力，在更大的固结压力作用下会使得土颗粒间发生相对移动变得更加不易，土体抵抗剪切破坏的能力有所增强。同时固结围压一定时，越大的固结比条件下，土样的动应变要想达到相同大小，需要施加更高水平的动应力，因为固结比越大，土体中土颗粒之间的连结更为紧密，土体愈不易产生变形，要使试样变形就需要更大的能量，故需要施加更大的动应力。

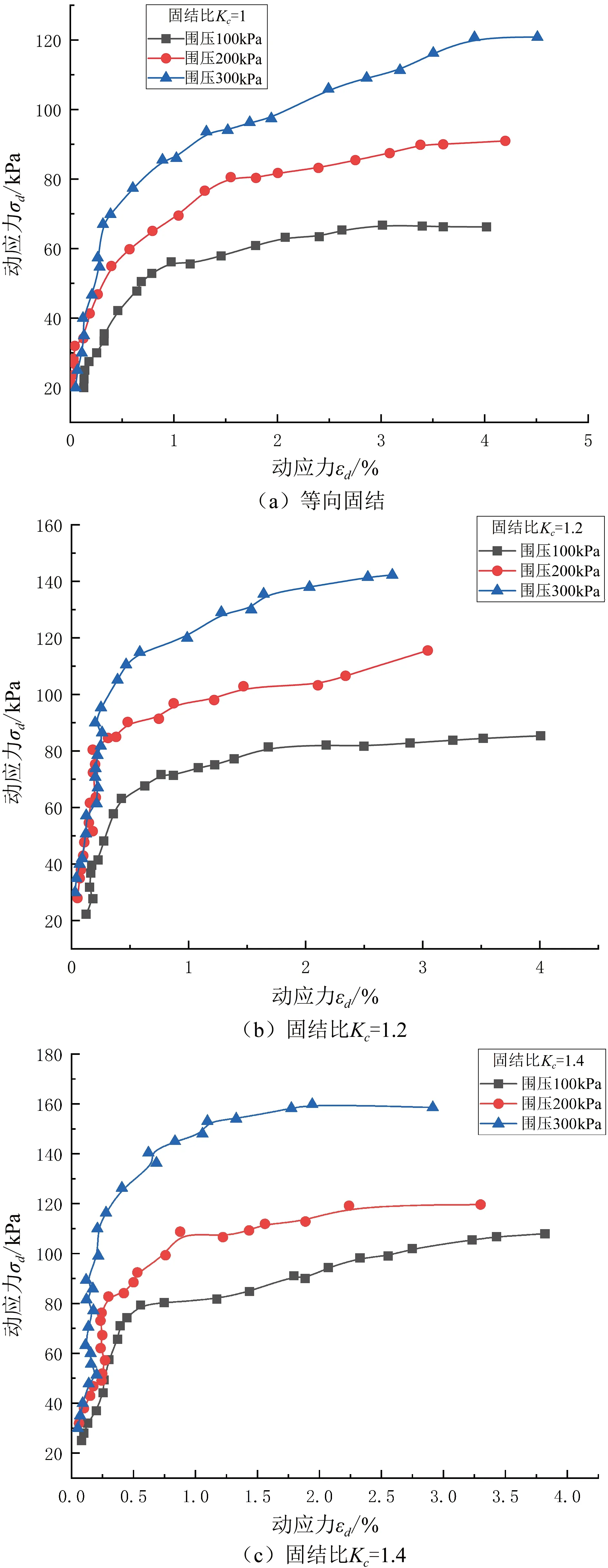
图1 呈贡地区红土动应力-应变关系曲线Figure 1 Laterite dynamic stress-dynamic strain relationshipcurve in Chenggong area

2.2 动剪切模量

动剪切模量Gd与静剪切模量类似，是表征土体在遭受动荷载作用下抵抗切应变的能力[6]。具体的计算公式如下：

(1)

τd=0.5σd

(2)

γd=(1+μ)εd

(3)

式中：Gd为动剪切模量，MPa；τd为动剪应力，kPa；γd为动剪应变；μ为泊松比；σd为动应力，kPa；εd为动应变，%。

由于本次试验采用的红土试样为饱和样，排水条件为固结不排水，故μ取0.5；根据试验结果分别计算Gd、γd，作出Gd-γd的关系曲线，以在100，200，300 kPa围压下等向固结的情况和在100 kPa下偏压固结(Kc=1.0，1.2，1.4)的情况为例，如图2所示。

由图2(a)可以看出，在对试样施加动荷载进行加载的初期阶段动剪切模量较大，随着试验继续进行，动剪应变增大，而动剪切模量随之降低，根据已有的研究[6-8]及经验判断土样产生刚度软化；在试验的初期阶段，此时Gd-γd的关系曲线斜率较大，说明此时土样的软化速率较快。而随着试验的继续进行，动剪应力加大，Gd-γd的关系曲线斜率逐渐减小并趋于平缓，说明其软化速率逐渐变慢。这是由于在试验的初始阶段加载的动荷载较小，此时土体的结构较为稳定，具有较强的抵抗动剪切的能力。继续加大动剪应变，土体中土颗粒发生错动，土颗粒的相对位置发生改变形成新的结构骨架，土体结构开始逐渐被破坏，并且对试样反复加载动荷载作用下，土体内部聚集了大量的能量，土颗粒之间的连结也变弱，其抵抗动剪应变的能力降低，故动剪切模量减小。当动剪应变增加到一定大小时，土体的结构被完全破坏，其动剪切模量大小趋于稳定。除此之外，由图2(a)中还可以看到固结围压越大，其动剪切模量的值越大，即固结围压越大，土体抵抗动剪应变的能力越强。这是由于土体中的土颗粒在固结围压作用下结合的更为紧密，固结围压越大，要使试样达到相同的动剪应变所需的动剪应力更大。

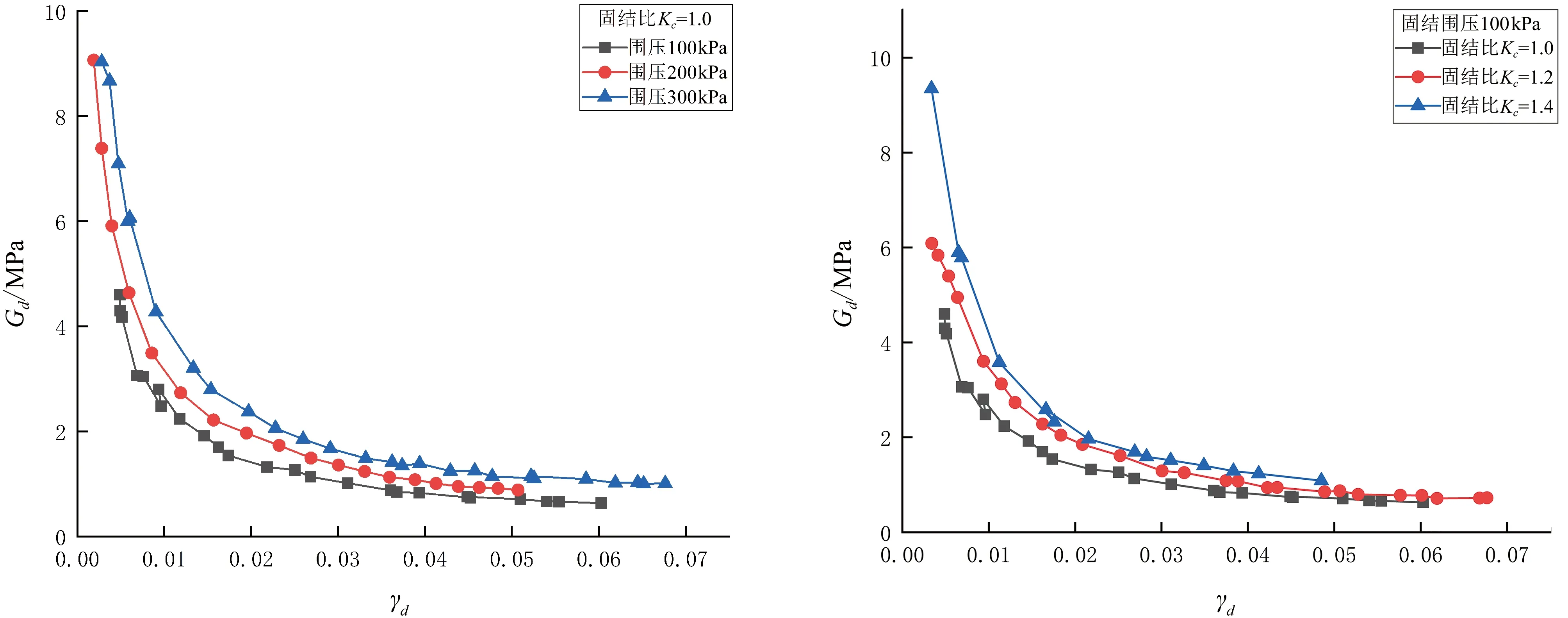
(a)不同围压 (b)不同固结比图2 呈贡红土Gd-γd关系曲线Figure 2 Chenggong laterite Gd-γd relationship curve

由图2(b)可以看出，土样在不同固结比Kc条件下的Gd-γd的关系曲线的形态及发展趋势，发现其与土样在不同固结围压下的Gd-γd的关系曲线形态基本一致。当将固结比Kc作为单一变量时，固结比愈大，土样的动剪切模量值也愈大。由于固结比愈大，土体中土颗粒轴向之间的连结越紧密，土体刚度更大，故抵抗动剪切的能力也越强，要想使试样发生剪切破坏就需要施加更大的剪应力。实际上，土样的固结比Kc越大，则土样的初始剪应力也更大，在相同动剪应变时自然土样的动剪切模量越大。继续对试样施加循环荷载，动剪应变逐渐增加，能量在土体内部大量聚集，土颗粒之间的连结作用逐渐开始变小，动剪切模量值逐渐减小最后趋于平稳。

2.3 阻尼比

土的阻尼是研究土动力特性的重要参数之一，该参数可以反映出土体在受到动荷载作用时，内部能量因土颗粒相互摩擦而逐渐消散的特性。土的阻尼比可根据动应力-应变滞回曲线求出，计算公式如下：

(4)

式中：AL为土体滞回圈面积；AT为图3所示的阴影面积。

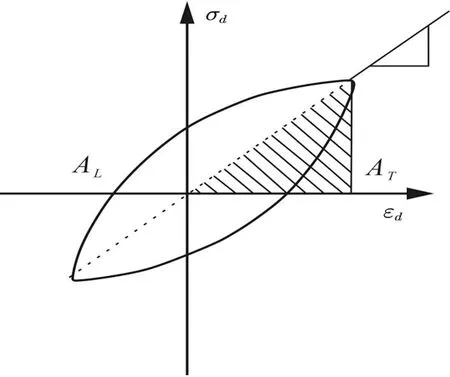
图3 滞回曲线与阻尼比Figure 3 Hysteresis curve and damping ratio

对试验数据进行处理得到红土在不同固结围压下的阻尼比与动剪应变的变化关系图，如图4所示。

由图4(a)中可以看到，随着动剪切应变的增加，该地区红土的阻尼比分布较为离散，但是总体上呈现波动升高的趋势。在动剪切应变较小时，土体的阻尼比也相对较小，其原因为在动剪切应变较小的情况下土体的结构近乎没有遭受到扰动破坏，土颗粒之间的相对错动位移较小，产生的摩擦也较小，从而使其抵抗剪应变的能量消耗较小。随着动剪切应变逐渐增加，阻尼比也渐渐增大，最后阻尼比的大小逐渐趋近于某一个定值即最大阻尼比，其原因为在试验的过程中逐渐增加动荷载的大小，动剪切应变逐渐增大，试样在动荷载作用下逐步开始产生破坏，从而使土颗粒之间的相对位移的范围加大，致使土颗粒之间的摩擦增加，所需要的能量也随之增加。在试验的后期，随着循环加载的次数以及动荷载的大小的增加，土颗粒之间的摩擦力也随之增加，但是由于土体被不断的压密，土颗粒之间的相对错动越来越小，因此所消耗的能量增速变缓，阻尼比逐渐趋近于某一定值。除此之外，固结围压越大其阻尼比越小，这是由于固结围压愈大，试样在围压作用下被压得越密，土颗粒之间结合越紧密，从而应力波在土体中传播越容易，因而阻尼比愈小。

由图4(b)在不同固结应力比的情况下，土体阻尼比随着动剪切应变变化，分布也较为离散，但总体上还是呈现波动升高的趋势，并且土体在动剪切应变一致时，固结应力比愈大其阻尼比也愈大。土体的固结应力比愈大，其初始偏应力愈大，而偏应力会破坏土体的结构，使得土颗粒之间更为松散，从而应力波不易在土体中传播，故固结应力比越大，阻尼比值越大。

实际上，土体的阻尼比随动剪切应变的变化，分布的较为离散，其原因为目前关于阻尼比的计算尚无完全合理的方法。对土体施加动荷载作用，湿度状态较低的试样会产生上部变粗的情况，而试样的下部基本不会发生变化，这种现象为试样的变形不均匀。但是在分析处理试验数据计算动应变时试样的长度是按照其总长度来计算的，从而导致阻尼比的值分布较为离散。此外计算过程中泊松比的取值也会影响计算出的阻尼比值，在试验过程中随着动应变的增大，泊松比不可能保持为一恒定值，而在对数据进行处理时将泊松比取为定值0.5与实际工况不符。另外，试验设备的测量精度也会对阻尼比的计算产生一定影响。

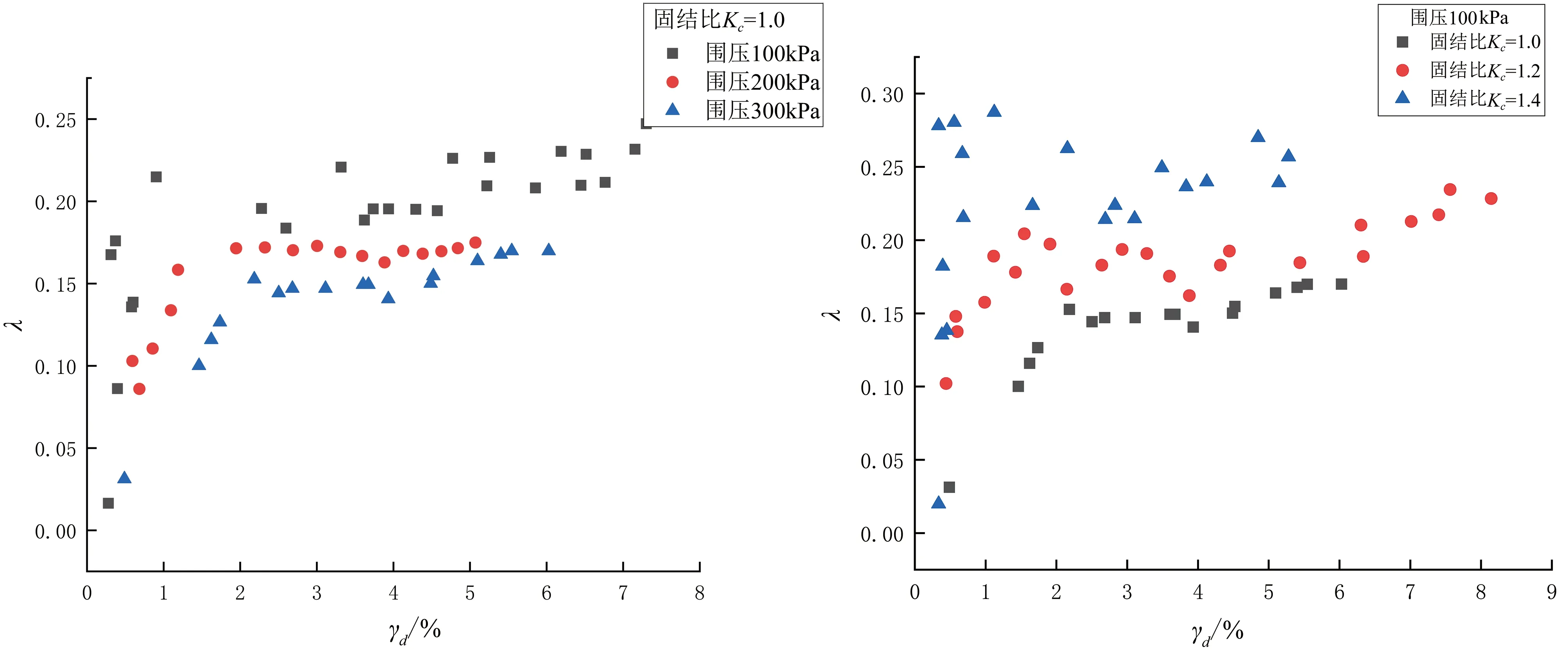
(a)不同固结围压下 (b)不同固结比图4 呈贡红土λ-γd关系Figure 4 Chenggong laterite λ-γd relationships

3 结论

1)呈贡地区红土的骨干曲线的变化规律呈现出明显的非线性关系，且符合双曲线模型。在动力作用下，可将红土的动应力-应变的发展分为三个阶段：第一阶段为近似弹性变形阶段，第二阶段土体开始出现塑性变形，第三阶段土体开始产生破坏。同时固结围压越大或固结比越大，若要使土体达到相同动应变值，则需要对土体施加更大动荷载。

2)呈贡地区红土的动剪切模量的值在初始荷载作用下较大，随着动剪切应变的增加，动剪切模量开始迅速降低，当动剪应变增加到某一值时，动剪切模量的值变化缓慢，基本维持在某一固定值附近。同时，在相同动剪应变情况下，土样的动剪切模量与固结围压及固结应力比均呈正相关。

3)随着动剪应变的增加，呈贡地区红土的阻尼比分布规律表现的较为离散，但是总体上呈现波动升高的趋势；土体的阻尼比值在其动剪应变较小的情况下也较小，随着动剪应变的增加，阻尼比也逐渐增大，而阻尼比不会无限增加，将会稳定在某个值附近即最大阻尼比。同时，阻尼比受固结围压以及固结应力比影响，与固结围压呈负相关，与固结应力比呈正相关。