基于卷积神经网络的直线同步电动机电枢绕组故障诊断*

王浩楠, 蓝益鹏

(沈阳工业大学 电气工程学院,辽宁 沈阳 110870)

0 引 言

机械故障诊断是现代工业中的重要技术[1]。直线同步电动机由于其可控性和高效率，在工业中有着越来越广泛的应用。电机的可靠性与工业生产的安全性密切相关。电机在长时间的运行过程中可能发生一些故障，如单相接地短路、绕组匝间短路和绕组断路等。轻微的短路故障若不加以重视，会导致严重的多匝线圈间短路，甚至发生其他更严重的故障，因此，必须对绕组故障进行可靠的检测[2]。

随着近些年深度学习领域的迅速发展，卷积神经网络(CNN)已经在故障诊断领域得到广泛应用[3]。Sun等[4]开发出卷积判别特征学习方法来对电动机进行故障诊断，该方法具有极高的鲁棒性和有效性。王丽华等[5]对振动信号进行短时傅里叶变换并通过CNN实现了电机故障诊断。尽管振动信号分析在故障诊断中能取得良好的结果，但是消除背景噪声通常是一个复杂的过程。振动测量还受到安装位置不确定性的影响，需要在电动机上安装传感器，会带来额外的成本；另外，相邻机器也会影响振动测量。

利用电流信号分析来进行电动机故障诊断，可以减少背景噪声和其他机械干扰的影响。此外，如果将霍尔传感器集成到逆变器中检测电动机的电枢电流，则无需安装其他传感器[6]。杨大雷等[7]利用交流电压和电流信号中频域信号的相关性分析了交流电机系统的故障，提高了故障诊断、识别的准确性。Ince等[8]提出了一维CNN，可以直接对电流信号进行处理，极大地降低了运算量。Kao等[9]将具有退磁和半退磁故障的电动机在5种不同故障情况下的定子电流信号经过离散小波变换在一维CNN中进行故障诊断。文献[10]研究结果表明频域分析在电动机的故障诊断中具有潜在的应用。一般来说，最直接地提升神经网络性能的方法就是扩展网络的层数和增加网络的宽度，但这也意味着需要大量的参数，会大大增加计算量[11]。

针对以上问题，本文提出一种基于绕组函数理论的CNN故障诊断方法。对直线同步电动机的电枢绕组进行仿真，利用CNN中GoogLeNet架构有效防止网络过拟合，对直线同步电动机匝间短路故障时电枢绕组的三相电流信号通过快速傅里叶变换(FFT)后的频谱图构建数据集，实现直线同步电动机电枢绕组的匝间短路诊断。

1 直线同步电动机的结构及其运行机理

1.1 直线同步电动机平台的结构

直线同步电动机平台的结构如图1所示，主要由电枢绕组、动子铁心、励磁绕组、电涡流传感器、光栅尺、导轨、基座平台和运动平台构成。

图1 直线同步电动机平台结构

1.2 直线同步电动机的运行机理

在直线同步电动机运行时电枢绕组通入三相对称交流电，在气隙中产生水平运动的行波磁场；励磁绕组通入直流电励磁，在气隙中产生励磁磁场。行波磁场与励磁磁场相互作用产生电磁推力使平台作直线运动。动子磁芯与励磁磁极间存在磁悬浮力，当磁悬浮力与平台重力相等时，平台将稳定悬浮[12]。

2 直线同步电动机的数学模型

2.1 绕组函数理论分析

在直线同步电动机中，对任意绕组，根据安培环路定律有：

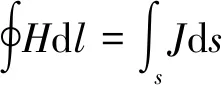
(1)

∮Hdl=na(x,x′)×ia

(2)

式中：H为a相绕组的磁场强度；J为电流密度；ia为a相绕组电流；na(x,x′)为a相绕组的绕组函数；x为从定子a相轴线算起的空间位移；x′为动子的位置。

根据磁通连续定理：

∮Bds=0

(3)

可以推导出a相绕组的磁动势：

Fa(x,x′)=Ma(x,x′)×ia

(4)

式中：B为绕组的磁感应强度；Fa(x,x′)为ia在a相绕组中产生的磁动势；Ma(x,x′)为修正过后a相绕组函数。且有：

Ma(x,x′)=na(x,x′)-〈Ma(x′)〉

(5)

(6)

磁动势F和磁导Λ的乘积为磁通φ：

φ=F×Λ

(7)

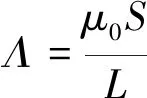
(8)

式中：μ0为真空磁导率；S为磁路的截面积；L为磁路的长度。

磁路的磁阻主要是气隙磁阻。直线同步电动机中的气隙不均匀，致使气隙的长度为动子位置的函数g(x,x′)，g-1(x,x′)为直线同步电动机气隙的倒函数。即：

(9)

(10)

(11)

直线同步电动机磁通的变化量为

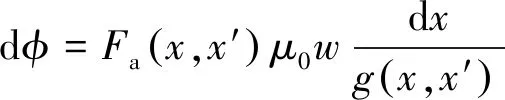
(12)

则a、b两相绕组的互感为

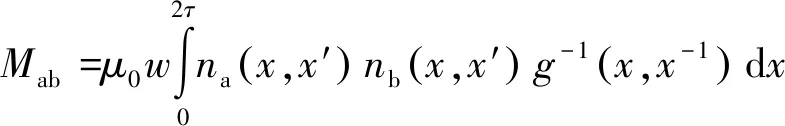
(13)

式中：nb(x,x′)为直线同步电动机b相绕组随位置变化的绕组函数。

从上述推导过程可以看出绕组函数理论可以应用于各种气隙分布的直线同步电动机。因此，本文以绕组函数理论为基础进行数学建模计算并对直线同步电动机进行仿真。

2.2 直线同步电动机电枢绕组数学模型

电枢绕组由三相绕组和铁心构成，以Y型连接。为了对模型进行分析和简化，作以下假设：(1)在忽略铁磁材料的饱和效应后，可以近似地认为直线同步电动机的磁动势全部落在气隙中，因此磁路的主要磁阻是气隙磁阻；(2)由于直线同步电动机结构的对称性，在数学模型中只模拟了一对磁极。理想直线同步电动机的数学模型可以看作是由电枢绕组和励磁绕组组成。

基于等效磁路法的直线同步电动机电压方程如下。

电枢回路的电压方程：

(14)

励磁回路的电压方程：

(15)

磁链方程：

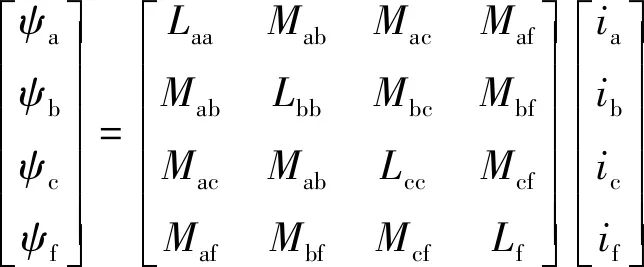
(16)

式(14)～式(16)中：r为电枢绕组的总电阻；rf为励磁绕组的电阻；Laa、Lbb和Lcc为各相电枢绕组的自感；Mij(i=a,b,c,f;j=a,b,c,f;i≠j)为线圈的互感系数。

对于直线同步电动机而言，根据以下公式进行简化：

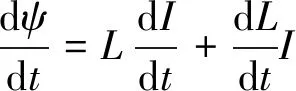
(17)

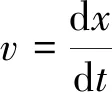
(18)

(19)

由式(17)和式(18)可得式(19)。将式(19)代入式(14)和式(15)可以得到直线同步电动机的数学模型公式：

(20)

式中：下标S和R用于区分经过简化后的矩阵元素，具体可对照简化前的式(16)。

根据由此得到的数学模型进行仿真。

2.3 匝间短路故障的数学模型

根据文献[13]中的统计分析，在所有电动机故障中，匝间短路故障约占61%～77%。根据直线同步电动机电枢绕组的内部故障，通过计算和仿真得到电枢绕组短路故障状态下的电流，并以电枢电流作为判断电机故障类型的依据。

电压方程如下所示：

(21)

用于仿真直线同步电动机电枢绕组的主要参数如下：同步速度为0.99 m/s，电枢绕组电流频率为10.3 Hz，电枢电流为2.5 A。在进行故障仿真分析时，需要首先计算相关的故障电气参数，主要包括电枢绕组各支路的电流和电压，从而得出电枢电流等参数。

假设电机电枢a相绕组发生了短路，如图2所示，电枢绕组的电压将被分成两部分ua1和ua2，相应的电枢绕组电感矩阵、电阻矩阵、电压方程都发生了变化。

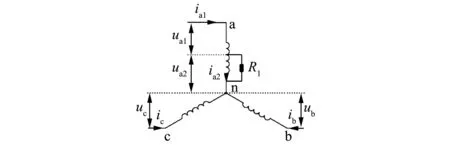
图2 电枢绕组a相短路电压分布

此时电压方程为

(22)

U′=[ua1,ua2,ub,uc,uf]T

(23)

I′=[ia1,ia2,ib,ic,if]T

(24)

式中：ua1为电枢绕组a相绕组未短路部分的电压；ua2为电枢绕组a相绕组短路部分的电压；ia1为电枢绕组a相绕组未短路部分的电流；ia2为电枢绕组a相绕组短路部分的电流。

变化后的电感矩阵和电阻矩阵展开为

(25)

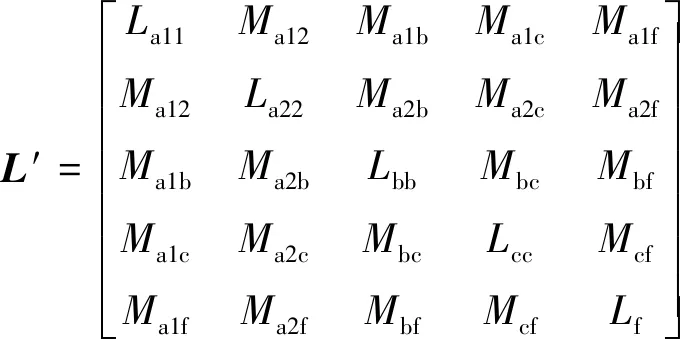
(26)

式中：ra1和ra2为电枢绕组a相未短路部分和短路部分电阻；La11和La22为电枢绕组a相未短路部分和短路部分的自感；Ma12为电枢绕组a相未短路部分与短路部分的互感；Ma1b为电枢绕组a相未短路部分与b相的互感，Ma1c、Ma1f同理；Ma2b为电枢绕组a相短路部分与b相的互感，Mac2、Ma2f同理。

假设b相和c相绕组发生匝间短路，绕组电压分别被分成了两个部分ub1和ub2、uc1和uc2，如图3所示，则相应的电枢绕组电感矩阵、电阻矩阵、电压矩程同样也都发生了变化。

此时电压方程为

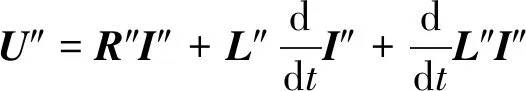
(27)

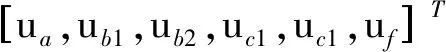
(28)

I″=[ia,ib1,ib2,ic1,ic2,if]T

(29)

其中：ub1和ub2为电枢绕组b相绕组未短路部分和短路部分的电压，uc1和uc2类似ub1和ub2。

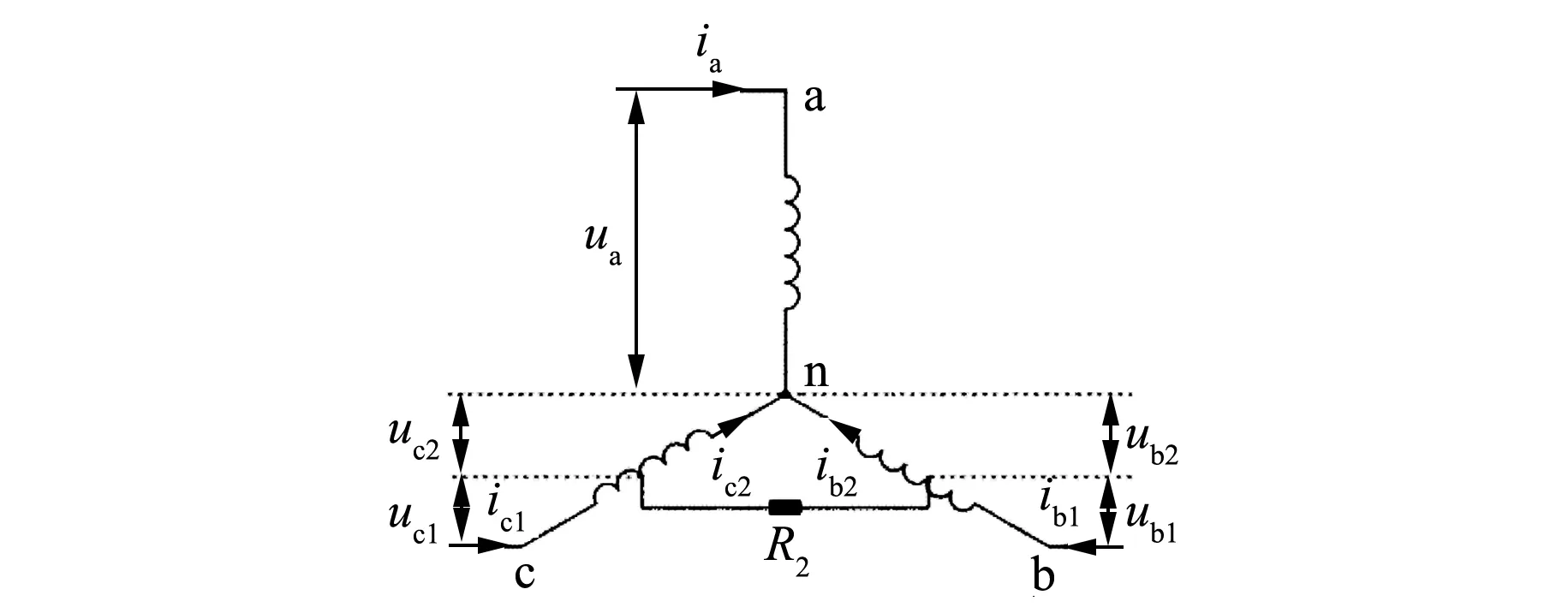
图3 电枢绕组b、c相匝间短路电压分布

变化后的电感矩阵和电阻矩阵展开为

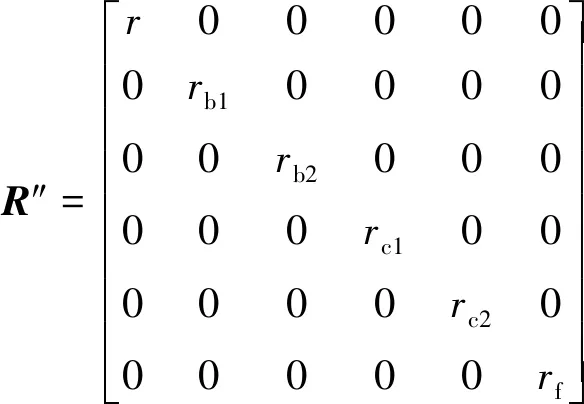
(30)

(31)

式中：rb1、rb2、rc1、rc2分别为电枢绕组b、c相未短路部分和短路部分的电阻；Lb11和Lb22为电枢绕组b相未短路部分和短路部分的自感，Lc11和Lc22同理；Mb1c1为电枢绕组b相未短路部分与c相未短路部分的互感；Mb1c2为电枢绕组b相未短路部分与c相短路部分的互感，Mb2c1同理；Mb12为电枢绕组b相未短路部分与b相短路部分的互感，Mc12同理；Mab1为电枢绕组a相和b相未短路部分的互感，Mab2、Mac1和Mac2同理。

3 基于CNN的故障诊断

3.1 网络架构

CNN主要由卷积层、池化层和全连接层组成[11]。卷积层通过卷积核提取图像的局部特征，并通过激活函数得到新的特征图像。池化层通常降低特征图像的维度，以保持局部特征不变，减少计算量。最后一层的池化层输出每个图像区域的高级特征，然后需要将这些非线性特征以一种简单的方式组合起来。最后，全连接层用来对输入图像进行分类。

从零开始训练深度CNN很耗时，而且需要大量的训练数据，因此CNN难以广泛应用。GoogLeNet是一种预训练CNN架构，其框架主要包括卷积层、池化层、全连接层、softmax层以及分类输出层。GoogLeNet框架结构如图4所示。

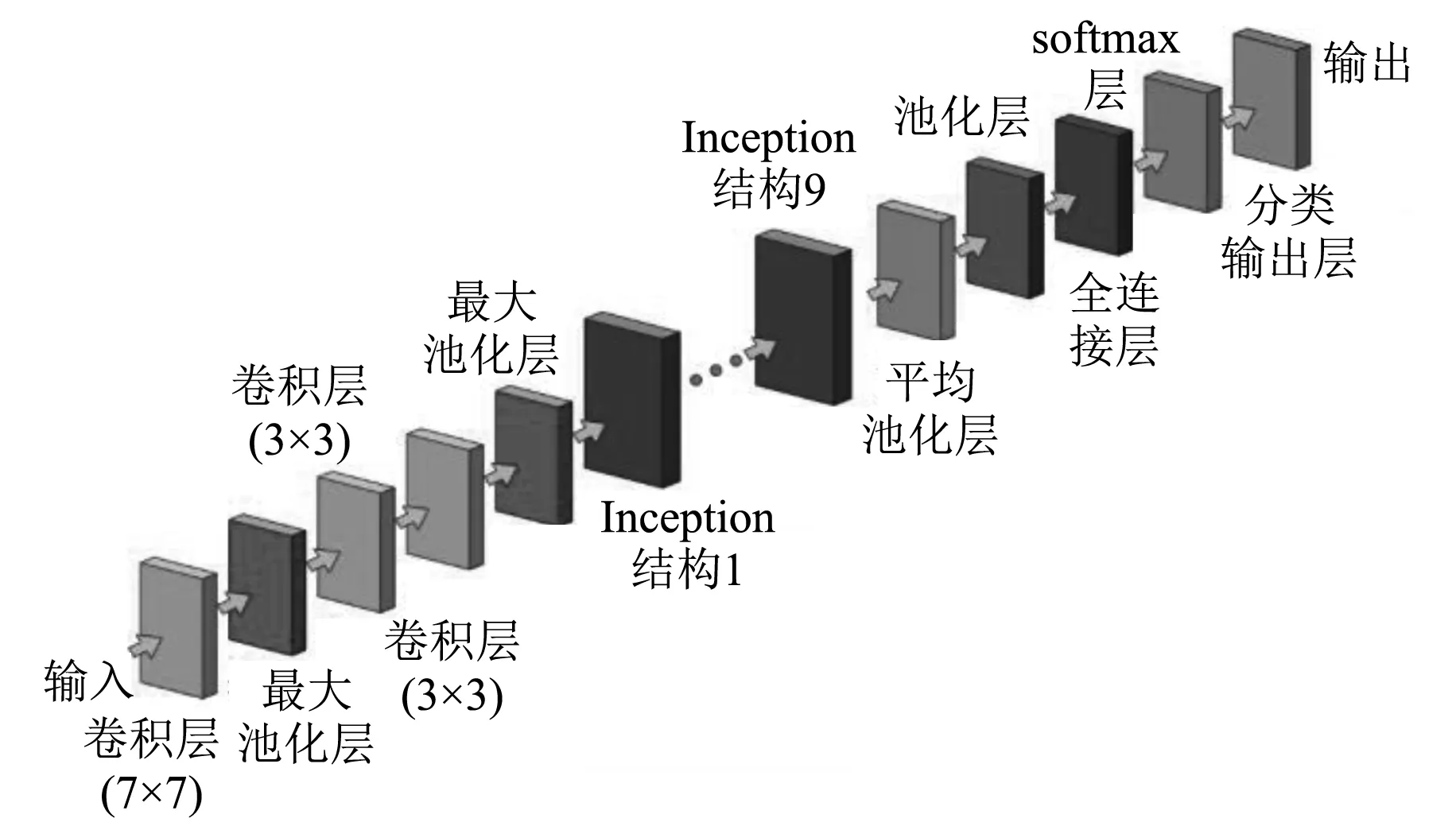
图4 GoogLeNet框架结构

在GoogLeNet框架中，Inception模块的基本机构如图5所示，深度为9层，整个Inception结构就是由多个这样的Inception模块串联起来的。Inception模块的主要作用有：(1)采用1×1的卷积来保持空间维度；(2)通过卷积核横向排列设计降低运算复杂度。

图5 Inception模块结构

3.2 构建数据集

电流信号取样流程如图6所示。根据2.2节中建立的直线同步电动机的正常状态的数学模型进行建模，再根据2.3节中对直线同步电动机电枢绕组匝间短路的分析构建故障模型，从而得到直线同步电动机电枢绕组正常状态和短路故障状态下电枢绕组的电流波形图，利用FFT将电流信号转换为时频信号，得到时频谱图，从而提高整个识别系统的准确性。

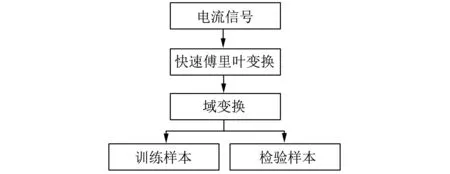
图6 电流信号取样流程图

通过MATLAB仿真收集100张匝间短路故障训练样本，各图像大小相同。将其中80%作为训练样本，20%作为检验样本，即训练集数据80张，检验样本20张。

图7为电枢绕组正常状态的电流波形图。图8和图9分别为电枢绕组a相匝间短路故障和b、c相匝间短路故障时的电流波形图。

图7 电枢绕组正常状态的电流波形图

图8 电枢绕组a相匝间短路故障时的电流波形图

图9 电枢绕组b、c相匝间短路故障时的电流波形图

利用FFT将电流信号转换为时频信号，得到的时频谱图如图10～图12所示。

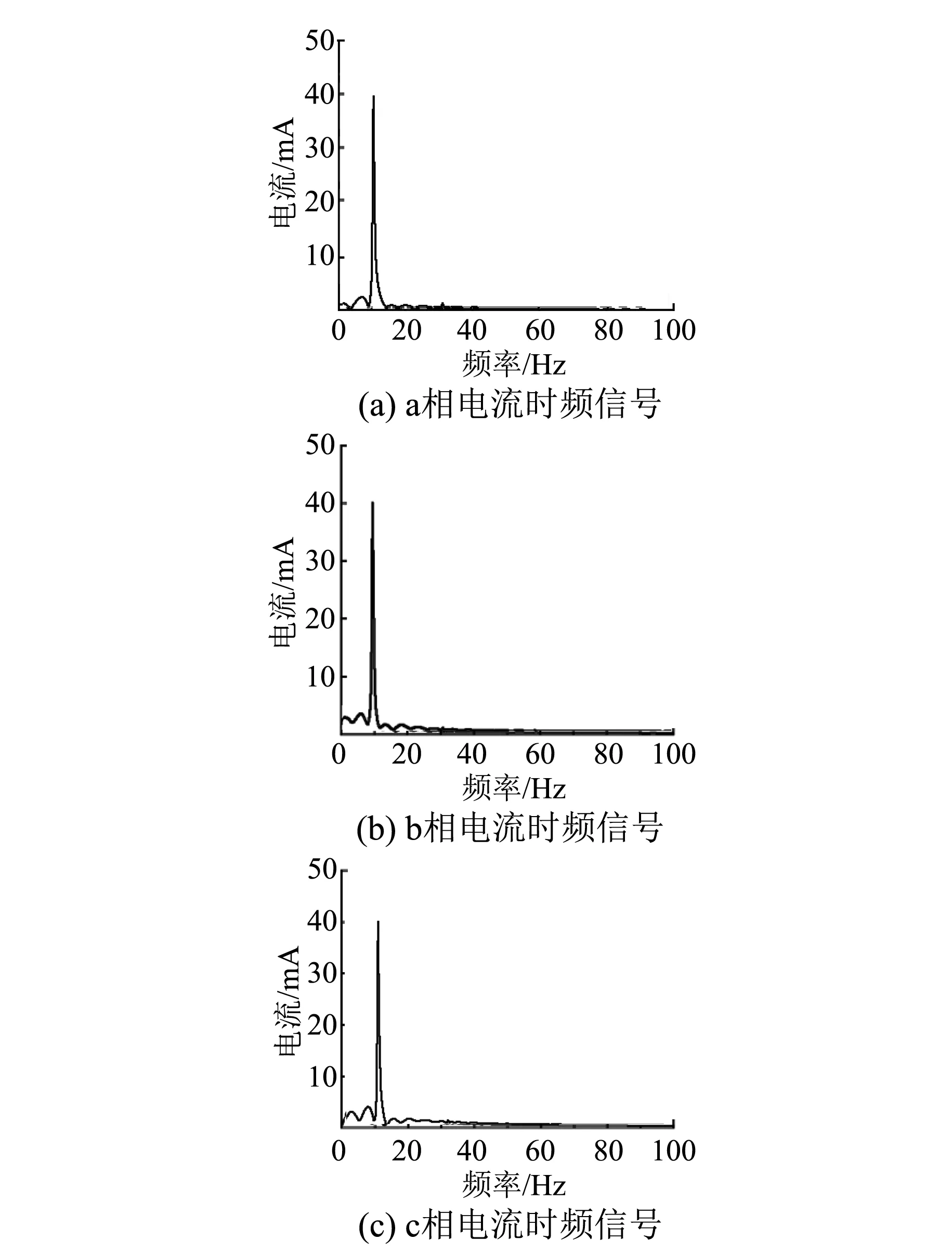
图10 电枢绕组正常状态的电流信号时频谱图

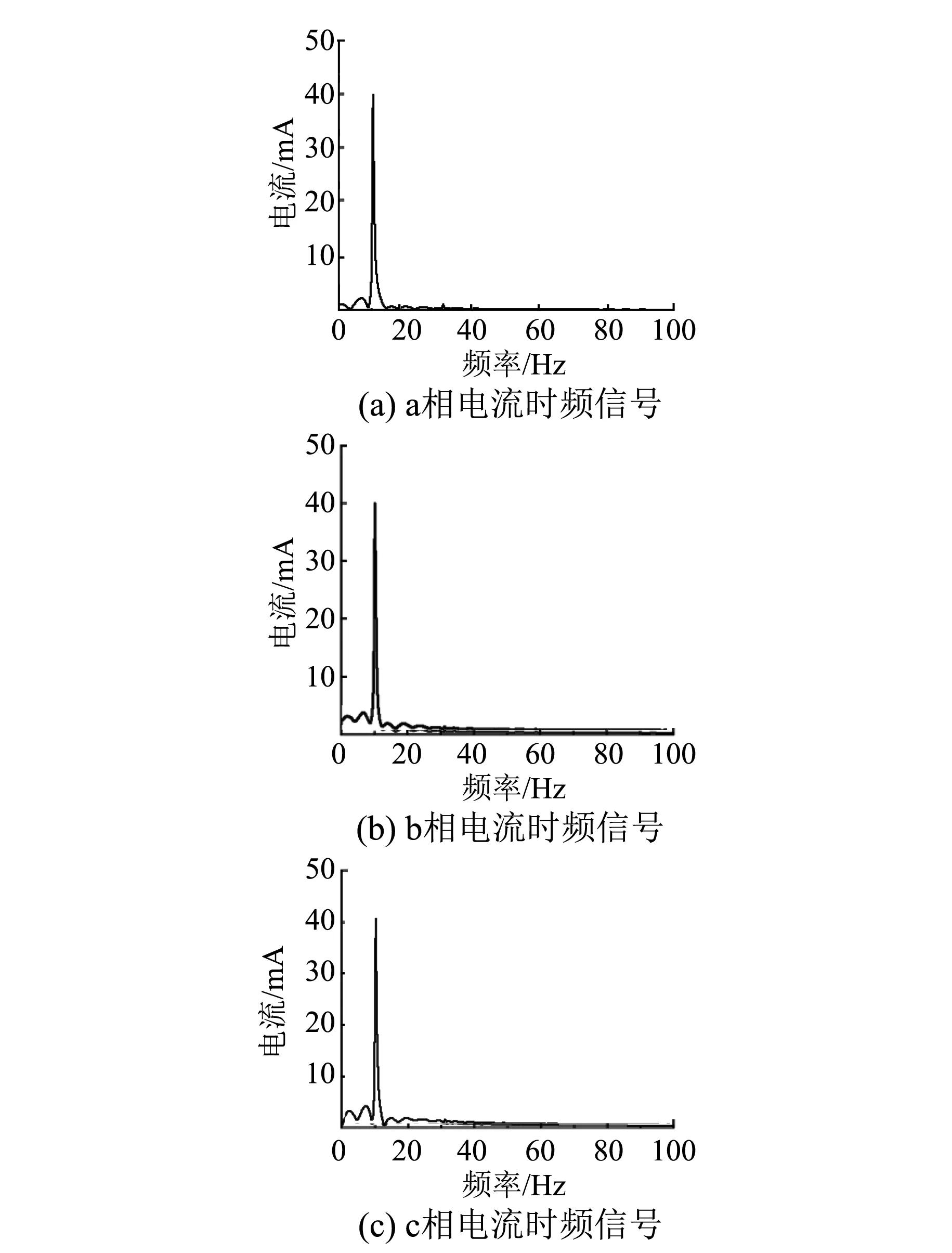
图11 电枢绕组a相匝间短路故障时的电流信号时频谱图

图12 电枢绕组b、c相匝间短路故障时的电流信号时频谱图

3.3 仿真结果及比较

选择不同的激活函数对网络完成训练的时间是不同的。常用的激活函数有tanh函数、Sigmoid函数和ReLu函数。表1列出了以上3种常用的激活函数在相同情况下对相同的数据集完成训练所需的时间。由表1可知，tanh函数和Sigmoid函数完成训练的时间基本相同；ReLu函数完成训练的时间低于以上两种函数。因此，ReLu函数更适用于训练GoogLeNet架构。

表1 不同激活函数对应的网络训练完成时间 min

学习率作为网络中的重要参数，决定目标函数能否收敛到局部最小值以及何时收敛到最小值。合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。损失函数是指网络对数据在多大程度上不拟合，损失函数的数值越小则证明拟合越好，过程中损失函数的数值越小反映出模型的鲁棒性越好。因此，选择一个合适的学习率对于网络的训练至关重要。图13为不同学习率对网络损失函数的影响。由图13可以看出学习率为5×10-5时，在迭代200次后损失函数更小，梯度稳定性更好。因此，5×10-5为最适合本网络的学习率。

图13 不同学习率对网络损失函数的影响

在训练过程中，设置学习率为5×10-5，每批训练量为10张图片，将整个数据集循环200轮，每轮的迭代次数为24,检验样本的频率为100，即每训练100轮将检验样本拿回网络构架对比准确度。图14为GoogLeNet架构模型准确率、损失与训练次数之间的关系。

由图14可见，随着迭代次数的增加，训练集准确率逐渐趋于100%，损失函数在1 000～1 500步之间逐渐收敛，而且检验集的准确率和训练集的准确率逐渐趋于相同。该方法的准确率在96.5%以上。虽然存在一定的漏识别和误识别情况，但避免了复杂的人为设置过程，能够从已知数据中区分正常状态和匝间短路状态，可以实现对电枢绕组匝间短路故障的诊断。

图14 网络迭代200轮4 800次结果

4 结 语

本文基于绕组函数理论对直线同步电动机进行分析，分别对正常状态和匝间短路状态建立相应的数学模型。在此基础上，提出了一种基于CNN中GoogLeNet架构的直线同步电动机电枢绕组短路故障诊断方法。经过激活函数和学习率的比较分析，选出了最适合所用网络框架的参数，有效避免了网络过拟合。经检验，准确率稳定在96.5%以上，可以实现对电枢绕组匝间短路故障的诊断。