全封闭大功率永磁牵引电机的温度场数值计算

张 伟, 庞 聪, 张 洁, 贾喜勤, 刘永强

(1.中车永济电机有限公司，陕西 西安 710016；2.西安中车电气研究院，陕西 西安 710016)

0 引 言

牵引电机采用全封闭型式具有防护等级高、维护频率低、能够适应复杂环境的优点，与开放式电机相比，可以避免风沙、尘土和雨水对绕组绝缘的侵蚀，提高绕组的寿命。但全封闭电机比开放式电机散热更为困难。如今随着动车组速度等级的不断提高，对牵引电机转速、功率及功率密度要求不断提升，导致全封闭电机的冷却系统设计难度不断增加，对电机设计阶段温升校核也提出了更高要求。

在计算电机温升时，常用的计算方法包括集总参数热网络法、有限元法和有限体积法，国内外对各类型全封闭电机的冷却方式和冷却结构均进行了研究。研究的电机大多采用散嵌绕组，针对散嵌绕组涉及的定子槽部导热模型简化问题。文献[1]提出了利用槽空率和槽绝缘导热系数计算小型电机散嵌绕组槽绝缘等效导热系数的公式。文献[2]通过绝缘等效对全封闭扇冷式异步电机建立了实际绕组等效模型，即采用等效模型与导热系数的方法对绕组及其绝缘进行处理，对电机的温度场进行了计算。文献[3]建立机壳水冷全封闭永磁电机的三维流固耦合共轭传热模型，研究了转子结构对转子散热的影响。文献[4]利用文献[1]提出的方法计算槽绝缘等效导热系数并对一款采用混合冷却方式的全封闭永磁发电机进行了温度场分析。

对带有水套的全封闭电机温度场进行计算，除了要考虑绕组导热模型简化外，电机水套与定子铁心之间的接触热阻也不能忽略，文献[5]对全封闭水冷永磁电机定子铁心、机座接触热阻的阻值进行了试验测试，发现定子铁心与机座接触热阻的阻值与损耗无关，不同方位的接触热阻阻值相差较小，平均值为0.001 52 ℃/W。文献[6]通过试验测试了电机机座和定子铁心之间接触热阻抗的大小，定子铁心表面未抛光的定子铁心-机座接触热阻抗值为1.955×10-4℃·m2/W，并分析了表面抛光、配合压力和使用导热硅脂对接触热阻的影响。

通过以上分析可以发现，对于采用双层成型绕组的大功率全封闭电机，相关的温度场研究较少，尤其是缺乏关于该类电机定子槽部绕组导热的分析。本文对一款采用成型绕组的额定功率为815 kW的牵引永磁同步电机进行了分析，首先建立了电机整机共轭传热模型，考虑旋转磁化、冲压过程和磁密高阶谐波对定子铁耗的影响，采用有限体积法对电机温度场进行分析。然后对样机进行了试验测试，对比了仿真与试验结果；并进一步对全封闭水冷永磁电机的流场、温度场分布特性以及水套—定子铁心接触间隙对绕组平均温升的影响进行了详细分析，提出该类全封闭电机散热优化的方向。

1 电机流场及温度场模型

1.1 数学模型

流动与热交换现象普遍地出现在自然界及各个工程领域中，所有流动与传热过程均受最基本的3个物理规律的支配，即质量守恒、动量守恒及能量守恒，对于稳态情况，控制方程的通用形式为[7]

div(ρUφ)=div(Γφgradφ)

(1)

式中:ρ为密度；φ为通用变量;U代表速度矢量；Γφ为广义扩散系数；Sφ为广义源项，不同求解变量之间的区别在于Γφ和Sφ的不同。

电机内固体需要满足传热方程[8]为

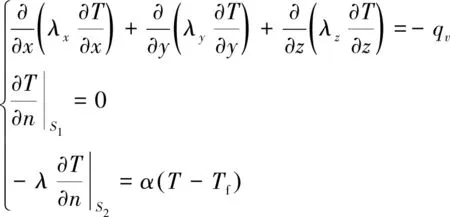
(2)

式中：T为待求温度；λx、λy、λz为求解域内各种材料沿x、y、z方向的导热系数；qv为单位时间、单位体积中内热源的生成热；α为对流散热系数 ；Tf为周围流体温度;S1为求解域中的绝热面;S2为求解域中的散热面。

该电机冷却通路包括水路和内循环风路，经计算雷诺数分别为27 400和4 070,均可采用湍流模型求解，本次计算采用Realizablek-ε湍流模型。

1.2 物理模型

该永磁电机转轴上装有离心风扇，机壳四角带有风路，与转子通风孔及线圈端部空间形成内循环风路。机壳与铁心之间带有轴向“Z字型”水路，电机冷却结构[9]如图1所示。

图1 电机冷却结构[9]

1.3 基本假设

该永磁电机定子绕组为斜槽双层形式，排列较为复杂，为了合理简化求解过程，做出以下假设:

(1) 定子绕组等效为直槽形式，简化过程中保持线圈外形基本不变，单个线圈简化结果如图2所示。

图2 简化线圈

(2) 定子槽内包括电磁线、主绝缘，槽底垫条、层间垫条、槽楔和绝缘漆。为详细研究槽内导热情况，保持定子铁心槽和上下层绕组截面尺寸不变，保留垫条和槽楔，电磁线简化为铜块;主绝缘和绝缘漆简化为包裹在铜块周围的同一材料的等效绝缘。成型绕组槽部导热简化模型如图3所示。

图3 成型绕组槽部导热模型

(3) 由于电机产生的热量大部分由水路带走，该散热通道要经过定子铁心外圆和电机水套之间的装配间隙。因此该间隙引起的接触热阻不能忽视，装配间隙计算公式采用[10]：

δ=(0.5+3d1)×10-5

(3)

式中：δ为装配间隙;d1为定子外圆直径。

通过式(3)计算该电机的装配间隙为0.019 4 mm。

1.4 边界条件

求解过程中，主要边界条件如下：

(1) 水路进口给定流量60 L/min，温度为41.3 ℃(试验时进水温度)，出口为压力出口；

(2) 由于电机产生的热量主要由水路带走，机壳及端盖外表面给定绝热边界[11]；

(3) 电机额定转速为4 800 r/min，转子旋转采用多重旋转坐标系(MRF)进行模拟，转子铁心、磁钢和转轴与流体接触的壁面均设置为旋转壁面；

(4) 由于电机运行过程中空气温度变化较大，分析时使用的空气物性参数模型随温度可变，其余结构材料导热系数为常数。绕组、磁钢、铁心、等效绝缘、转轴、端盖、机壳、压板和内循环风扇的导热系数如表1所示;

表1 电机各部件的导热系数

(5) 假设定子铁心与水套接触间隙内空气是静止的，通过接触面边界条件模拟该间隙，为便于计算，假设接触间隙内空气导热系数为常数，取接触面两侧温度平均值为定性温度。

1.5 电机损耗

电机额定工况(额定频率为240 Hz)下损耗包括定、转子铁心损耗，绕组铜耗，永磁体涡流损耗和机械损耗。绕组铜耗PCu计算公式为

PCu=mI2R

(4)

式中：m为电机绕组相数;I为相电流有效值；R为绕组的直流电阻值。

温升试验停止时记录电流并对绕组直流电阻值进行了测试，按照式(4)算得铜耗为7.37 kW。

计算铁心损耗常用经典Bertotti损耗分离模型，该模型将铁心损耗分为磁滞、涡流和附加损耗，为常系数铁耗模型，仅适用于磁密波形接近正弦，频率变化范围较小的情况，不能直接应用于高密度永磁同步电机铁耗计算。

为获得准确的电机铁耗，采用有限元方法对电机额定工况进行仿真。依据厂家提供的硅钢片损耗曲线及电机温升试验过程中电压、电流测试结果,在Maxwell 2D中对电机额定工况下定、转子铁耗及磁钢涡流损耗进行了分析，其中定子铁心分为轭部和齿部进行了计算。并分两步对定子铁耗进行修正。

第一步是考虑旋转磁化和冲片叠压过程对定子铁心损耗的影响，对磁滞损耗系数进行了修正。

文献[12]中采用以下磁滞损耗系数修正公式来考虑旋转磁化对电机铁心损耗的影响：

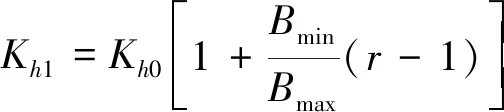
(5)

文献[13]中提到硅钢片在制造成为电机铁心过程中需进行冲压和剪切过程形成齿槽，冲压和剪切工艺将对铁心材料的磁滞损耗参数造成影响。为考虑该影响，采用公式(6)对上一步获得的磁滞损耗系数进行修正：

Kh=kcyKh1

(6)

式中:Kh1、Kh分别为在考虑旋转磁化基础上，考虑冲压和剪切过程修正前、后的磁滞损耗系数;kcy为经验系数，取1.6。

旋转磁化修正和剪切冲压修正前后磁滞损耗系数、涡流损耗系数和附加损耗系数结果如表2所示。

在Maxwell中输入修正后的铁耗系数，定子铁心铁耗计算结果如图4所示，定子铁心齿部、轭部和转子铁心损耗分别为6.00 kW、3.35 kW和

表2 定子铁心铁耗系数变化

图4 铁耗仿真曲线

0.61 kW。转子铁耗集中于转子表面附近，根据损耗分布仿真结果，将转子铁耗施加于转子铁心半径Rrotor>149.0 mm范围内，转子外径为160.7 mm。

第二步是采用公式(7)对定子铁心内磁密高频分量引起的高频铁耗进行计算[14]：

(7)

式中：Pn为高频磁密谐波引起的单位质量定子铁耗；β为磁滞损耗经验系数，取2；Ke为附加损耗系数；i为电机磁密谐波阶次；fi为磁密i阶谐波频率；Bir为径向磁密i阶谐波幅值;Bit为切向磁密i阶谐波幅值。

经计算，磁密高阶谐波在定子铁心产生的总损耗为2.38 kW，其中齿部1.83 kW，轭部0.55 kW，经过两步修正，电机定子铁心齿部和轭部损耗最终分别为7.83 kW和3.90 kW。

机械损耗包括轴承摩擦损耗、转子风磨和内风扇通风损耗，根据估算，通风损耗为624 W[15]，风磨和轴承损耗分别为233 W和377 W[16]，则机械损耗为1 234 W，忽略轴承损耗对电机铁心、绕组温升计算的影响，其余机械损耗为857 W，一半施加于转子铁心(除转子铁耗施加区域外)，一半施加于内风扇。最终电机各部件施加的热密值如表3所示。

表3 电机各部件热密值

2 网格划分

为获得电机温度场计算网格，依据1.3节假设对电机模型合理简化，简化后模型主要包括机壳、水道、两端端盖、定转子铁心、定转子压板、线圈、磁钢、内循环风扇、内循环风路和转轴。划分网格时，水道壁面划分边界层网格。为确定合适的网格参数，全局加密网格，选取总网格数目为2 712万、4 709万、5 954万、7 687万和9 372万的5组网格进行网格无关性验证，定子绕组平均温升及水路水阻计算结果如图5所示，兼顾工程要求和计算资源与时间的限制，最终采取5 954万网格，网格如图6所示。

图5 网格无关性验证

图6 网格剖面

采用5 954万网格计算完成后，查看水路的y+范围在0.09～24之间，内循环风路y+范围在0.1～154之间，可以看出，y+范围较广，覆盖了从黏性底层、过渡区到对数率区域的所有范围，计算采用Enhanced Wall Treatment壁面函数较为合适。

3 整机温升试验验证

为验证仿真计算结果，对样机在额定工况下稳态温升进行了试验测试，通过电机制造时埋入的温度传感器(热敏电阻PT100)测得电机定子铁心和绕组端部局部测点温度，采用电阻法测得绕组平均温升，试验现场布置如图7所示。

图7 电机温升测试现场

表4为电机额定工况下温升达到稳态时的定子铁心测点温升和绕组平均温升仿真与试验结果对比，通过试验测得定子铁心测点温升为67.4 K，仿真结果为67.1 K，绝对误差为-0.3 K；定子绕组平均温升为146.0 K，仿真值为142.3 K，绝对误差为-3.7 K。

表4 定子绕组平均温升及铁心测点温升对比 K

在电机嵌线过程中，将8支温度传感器安装在绕组两端端部距离铁心30 mm的上层边与下层边夹缝间，两端均按照“十字型”布置，两端各4支。由于局部测点温升受工艺影响较大，为了对比此处温升仿真与测试结果，仿真结果取上下层之间环面的平均温度，两端传感器所在截面位置及线圈温升分布如图8所示，截出的环面如图9所示。试验结果取各端4个测点的平均值。

图8 温度传感器所在截面位置及线圈温度分布

图9 温度传感器所处环面

表5比较了线圈两端端部传感器所在环面平均温度的仿真与试验结果。仿真与试验结果均表明绕组传动端端部温度要稍低于非传动端，这是因为内循环空气经过机壳通风道被水路冷却，温度降低，而空气继续流过绕组传动端端部、转子通风孔和风扇后，到达传动端端部绕组后，温度上升，即传动端绕组端部的冷却介质温度要低于非传动端。

表5 线圈端部测点平均温度对比 K

4 流场温度场分布及热阻影响

4.1 电机水路和内循环风路结果分析

电机水路流线如图10所示，大部分拐角处均有涡流存在，水道进口流速平均值为2.1 m/s，水路最大流速为8.0 m/s。电机水路壁面静压如图11所示，进口平均压力为162.0 kPa，试验过程中实测水压为160.0 kPa[9]，绝对误差为2.0 kPa。

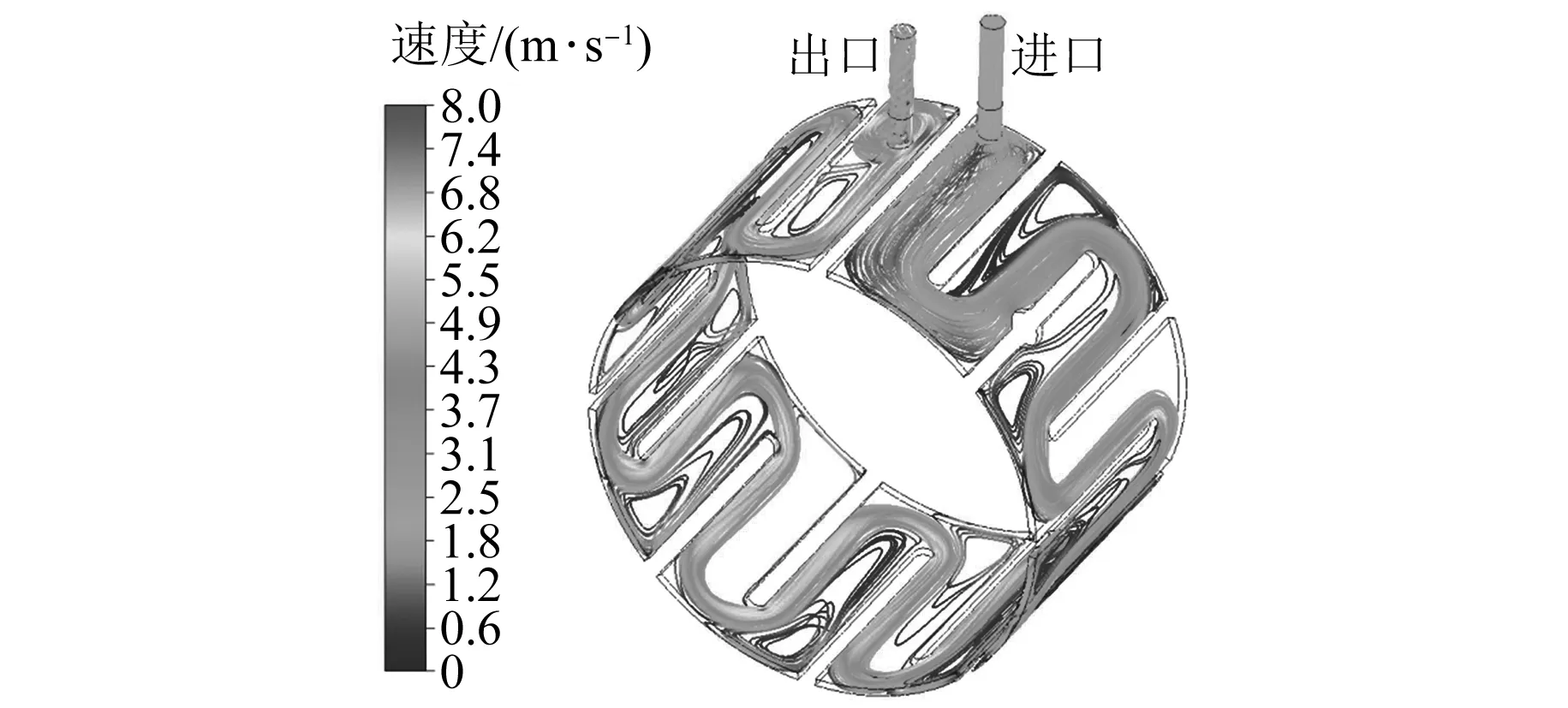
图10 电机水路流线图

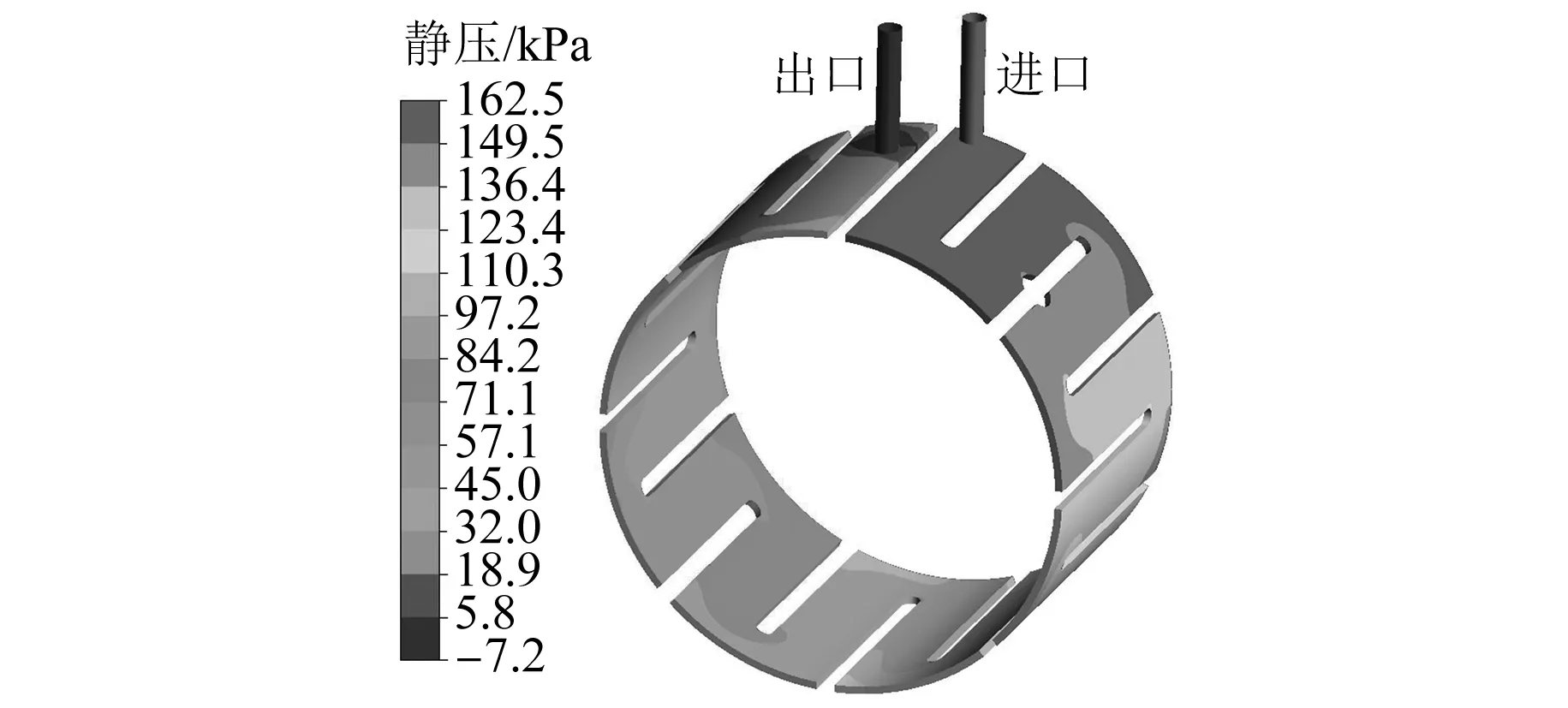
图11 电机水路壁面静压分布图

电机内循环风路速度分布如图12所示，最大速度约为80.8 m/s，内风路风量为5.5 m3/min。空气进入定子机壳内通风孔时的平均温度为109.2 ℃，离开机壳通风孔时的平均温度为84.2 ℃，温度下降了25.0 ℃，与机壳间换热量为2.1 kW，有效平衡了电机内部温升分布。

图12 电机内风路速度分布图

4.2 接触热阻抗对温升影响

为分析水套-定子铁心接触热阻抗对电机温升的影响，对接触间隙分别为0、δ/4、δ/2、3δ/4、δ厚度下接触热阻抗和电机绕组平均温升进行了计算，计算结果如图13所示。接触间隙减少一半，绕组平均温升降低了8.4 K，降幅较为明显；水套与定子铁心完全接触时，即没有接触间隙，绕组平均温升降低了18.1 K。

图13 水套与定子铁心接触间隙对绕组温升影响

4.3 槽内绕组温度分布

截取电机定子铁心中部轴向截面，电机槽内绕组温度分布及路径AB位置如图14所示，可以看出上层绕组温度明显高出下层绕组。

图14 铁心中部槽内绕组温度分布及路径示意图

图14所示路径AB依次经过气隙、槽楔、等效绝缘、上层线圈、等效绝缘、层间垫条、等效绝缘、下层线圈、等效绝缘、槽底垫条、定子铁心。该路径上的温度变化情况如图15所示，经计算，绕组在直线段区域，上层绕组平均温度比下层绕组高8.9 K；下层线圈与铁心槽的温差大约为51.7 K，定子铁心槽底到外圆的温降大约为29.3 K。

图15 AB路径上温度分布

结合以上分析，水套与直线段上层绕组平均温差为114.2 K，占线圈绕组平均温升的78%，其中影响较大的因素分别为绝缘热阻、定子铁心径向热阻和水套-铁心接触热阻，为降低电机温升，可以从提高绝缘整体导热系数、铁心径向导热系数和降低水套-铁心接触热阻等方面进行优化。

5 结 语

通过建立大功率全封闭永磁电机的流热耦合计算模型，对电机额定工况下稳态温度场分布进行了仿真与试验研究，验证了仿真方法的可靠性，同时提出了该类电机冷却系统设计优化方向，以下结论可以为电机设计制造单位在电机冷却系统提升方面提供参考：

(1) 磁密高阶谐波产生的定子铁耗为2.38 kW,占总铁耗的1/5左右，不能忽略其对电机温升的影响；

(2) 大功率永磁水冷电机同时采用内循环风路冷却效果较好，可以将转子和绕组端部区域的热量通过机壳通风道散出，有效降低了电机内部温升分布差异;

(3) 减小水套-定子铁心接触间隙可有效降低绕组平均温升，建议在电机制造过程中降低接触表面粗糙度和提高热套工艺质量来减小接触的间隙；

(4) 绕组绝缘两侧温差占绕组温升的1/3以上，是电机温升优化的重点，在电机绝缘系统设计中，应尽可能选用高导热绝缘材料。