粒子群算法在制造调度系统中的应用研究

王楚楚，臧海娟

（1.江苏理工学院 机械学院，江苏 常州 213001；2.江苏理工学院 计算机工程学院，江苏 常州 213001）

制造业在国家经济、社会发展中占着重要地位，它直接体现了一个国家的生产力水平。在制造业中，调度问题关系到企业整个生产系统的正常运转。制造调度系统的智能优化是现代制造和管理的核心[1]，它是针对制造系统中面临的各种动态事件，在满足约束条件的前提下，做出及时的响应，以实现生产的最优化[2]。粒子群算法是通过模拟鸟群搜捕食物的方法，找寻现实生活中问题的最优解。由于其实现简单、可调参数少、寻找结果效率高等优点，被广泛应用于制造领域调度问题，并取得了大量的成果。本文从算法在制造系统调度中的规划、优化和应用方面进行综述和分析。

1 粒子群算法及其演化

鸟类以群体为单位进行觅食，通过每只鸟不断的分享信息，找到范围未知的食物。受此过程的启发，美国的 Kennedy 和 Eberhart博士提出了粒子群算法。在粒子群算法（Particle Swarm Optimization，PSO）中，鸟群个体抽象为无质量无体积的粒子，粒子的位置为候选解。每个粒子初始化都有两个基本信息，即自身的位置和速度，通过信息基本交互得到个体和群体的最优位置，位置是否最优由适应度函数比较得出。

假设粒子的位置和速度分别用向量Xi，j=（xi，1，xi，2，…，xi，d）和Vi=（vi，1，vi，2，…，vi，d）表示，其中i为粒子编号，d为空间维度，i=1，2，…，n。则粒子的方程公式如（1）、（2）所示：

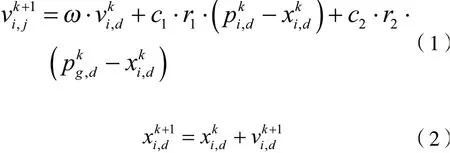
自粒子群算法提出以来，为解决其自身固有的缺点和获得更好更快的结果，众多研究者从参数修正、收敛性、混合PSO等角度对算法进行改进，让其在诸多领域发挥重大的作用。

1.1 参数的修正

PSO的参数的不同选择对算法性能有着不同的影响，对参数的改进有许多经典算法。

Zhang L，Tang Y，Hua C C等[3]将贝叶斯技术引入粒子群算法中，根据粒子过去的位置来调整惯性权值，使算法具有更高的精度和更快的收敛速度。2020年，杨宝军[4]从离散状态空间表达式入手，在惯性权重矩阵的基础上，提出一种提高收敛、跳出局部极数的自适应粒子群算法（RDR-PSO），得到的算法稳定性强、收敛精度有着一定的提升。同年，周旭和张业荣[5]对粒子群算法中的惯性权重ω和c1c2学习因子进行调整，使ω在前期数值较大，迭代后期数值较小，提出一种非线性变化策略，使c1逐渐减小，c2逐渐增大。薛建彬，刘星星[6]提出了基于PD公式的惯性权重函数，进行惯性权重的自适应选择。当种群多样性较好时，可通过减小惯性权重，使粒子找到更优的个体极值和全体极值。否则增加粒子速度，增强全局寻优的能力。

1.2 粒子群算法的收敛性

由于粒子群算法受随机系数影响较大，因此，许多研究者对算法收敛性进行了不同的分析、改进，以进一步提高算法的性能。

宋美、葛玉辉、刘举胜[7]针对PSO算法易陷入局部最优、发生早熟的缺点，提出一种动态双重自适应PSO 改进算法，文中采用Feigenbaum迭代构造混沌序列初始化粒子位置和速度，引用协同进化理论中的非线性调整策略来平衡c1、c2的关系，从而控制粒子的飞行方向和速度，提高收敛速度。Hao L，Zhang X W，Liang H等人[8]提出的基于人类行为的粒子群优化算法（HPSO），将全局最差的粒子引入到算法的速度方程中，该方程服从标准正态分布，具有随机权重且消除了两个加速度系数c1c2。HPSO通过上述方法降低已解决问题的参数敏感性，并改变粒子的飞行模式，从而提高种群的多样性、收敛速度和精度。

1.3 混合粒子群算法

在对PSO算法的改进中，多数情况下，PSO通过混合其他算法或技术来补足自身缺点。卢志刚，申康[9]提出蚁群算法与粒子群算法综合应用的混合算法， 以更准确更高效率地求解了供应链合作伙伴选择的问题；Tetsuyuki、 Takahama、Setsuko Sakai[10]提出将EPC方法应用于PSO，控制系数的扩展目标值相同，并将一个新的解与当前最优解比较；Chen M R，Li X，Zhang X等人[11]为了克服PSO的局限性，将PSO与极值优化（EO）相结合。Jiang H，Kwong C，K，Chen Z Q等人[12]结合混沌优化算法（COA）和PSO以得到更快的收敛速度及更高的迭代精度，对用于医疗的持续高温腹腔灌注的温度进行了预测控制。

2 制造系统中的粒子群算法

2.1 制造领域的研究现状

21世纪，大数据、人工智能、云计算等计算机技术的蓬勃发展，促使消费行为、企业模式产生巨大转变。德国工业4.0和国内《中国制造2025》的提出使得制造领域焕发出勃勃生机，将制造技术与数字技术、网络技术、智能技术等多种技术结合，打造智能化制造[13]。2010年，欧盟提出“欧洲2020的战略”，为了实现制造业上智能化的进一步发展。2011年，美国总统奥巴马提出“先进制造伙伴AMP”，在政府、企业、高校的合作基础上，强化制造业，创新和发展关键制造行业、机器人战略、先进材料等方面，进一步研发智能工厂、智能制造技术和智能制造平台。2012年，英国经济学家发表智能制造技术发展会引起“第三地工业革命”的言论[14]。2014年，日本推行“再行战略”，重点发展机器人、新能源汽车和3D打印等。近几年，我国也加大对智能化制造的重视，发布相关政策，加大对智能制造技术研究、高校研究、人才培养的投资，使得智能制造技术取得快速的发展，在机器人技术、通信网络技术、信息处理技术、传感器等方面有了大幅度的提升。我国起步较晚，现在与欧美国家有一定的差距，我们仍需不断创新、不断探索、不断发展，在未来谋取一片天地。

智能制造的目的在于实现整个制造过程的智能化，包括智能技术与产品设计、制造、装配、运输等产业链的深度融合。基于大数据的智能生产调度与优化技术是实现智能制造的关键技术之一，为了解决生产调度问题，应用了多种的基于人工智能的智能算法。制造业重视数据共享、调度的全局性和可扩展性、事件的响应速度等调度问题，促使研究者不断优化调度系统，改进调度方法。

2.2 粒子群算法与其他智能算法对比

制造系统中典型的智能算法包括遗传算法、粒子群算法、蚁群算法等，此类算法对问题依赖性较弱，通过计算机迭代运算完成搜索。遗传算法模拟了自然生物界遗传和进化过程优化方法，算法根据群体中个体的选择、交叉和变异操作获得更优秀的个体，该算法高效、鲁棒性强、全局搜索能力强，但实现较复杂，运行效率低。蚁群算法是受蚂蚁集体寻径行为启发而来，该算法形成一种正反馈机制，易于并行实现以及和其他算法结合，但参数较多，运行效率较低并容易发生停滞现象，适用小规模、低维数据。粒子群算法易于实现，局部搜索能力强且运行效率高，但易陷入局部最优，寻优精度低，适合较大规模数据。

2.3 粒子群算法在制造调度中应用

粒子群算法在制造调度中应用大致分为三种：一是将粒子群算法直接运用调度模型中；二是在粒子群算法的基础上改进算法后运用；三是粒子群算法结合其他算法融合在运用。

在粒子群算法直接解决调度方向上，Muharni Y Irman A，Febianti E等[15]使用PSO算法解决并行机流水车间调度中的调度问题。Nouiri M，Bekrar A，Jemai A等[16]以最小化最大完工时间准则为目标，应用粒子群优化算法求解柔性作业车间调度问题。Liao， J.和Lin， C[17]提出基于粒子群算法的作业车间供应链调度优化方法，并通过实例证明了粒子群算法能有效克服生产调度中的不收敛问题，以获得车间作业调度的最优解。Balaji A.N，Porselvi S，Jawahar N[18]使用粒子群算法解决多单元柔性制造系统中具有顺序依赖批量建立时间的零件批调度问题。

针对粒子群算法易陷入局部最优，寻优精度低等问题，提出改进方法解决调度问题。黎书文、张成龙、周知进[19]针对离散制造车间柔性调度优化，提出一种惯性权重、学习因子自适应调整的粒子群算法，并基于改算法建立柔性调度多目标优化模型。此算法基于1－ω＞0且2ω+2－c1－c2＞0的粒子稳定条件改进，更新公式如式（3） 、（4）所示：

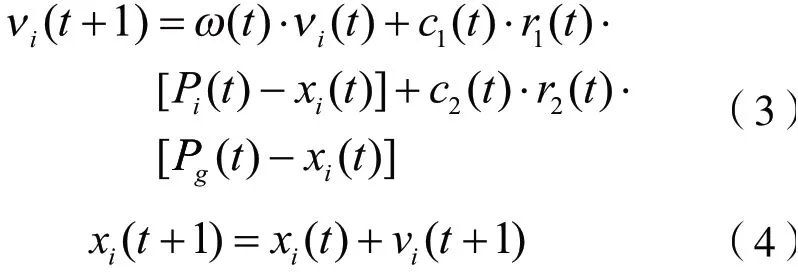
惯性权重余弦自适应调整可提高算法初期的全局寻优能力，运行过程中的逐渐递减有利于加速算法收敛。根据粒子稳定条件调整学习因子，提高了粒子学习能力。实验表明自适应调整的粒子群算法加快了收敛速度，增强了全局搜索能力，所以对车间调度的效率有着一定的提升。但自适应机制增加了算法的复杂度，执行时间较长，且改进算法只是和PSO算法、SA算法相比，缺乏更多算法的比较。温海骏、刘从虎[20]通过在粒子群算法中引入积分控制器，使用控制器控制粒子运行轨迹的方式解决不确定条件下再制造模糊加工时间的生产调度问题。Marichelvam M.K，Geetha M，Tosun O[21]在考虑人为因素的基础上，引入调度规则和建设性启发式来改进PSO算法的初始解，并混合变量邻域搜索算法和PSO算法，应用于各阶段具有相同并行机的多级混合流水车间调度问题。Chen S C，Cheng C F，Lin C C[22]提出了一种新颖的离散粒子群优化算法来求解资源受限项目计划问题，即在资源约束和优先约束的情况下，使项目的制造时间最小化。Anuar N I， Fauadi M H F M，Saptari A[23]为解决Job-shop调度问题，提出使用离散粒子群算法模型求解。

粒子群算法与其他算法结合进行优化是目前应用较广泛的手段之一。Li X Y，Gao L，Wang W W等[24]采用遗传算子重新定义粒子群算法，结合遗传算法和粒子群优化算法的优点来求解不确定的IPPS问题。公式如（5）所示：

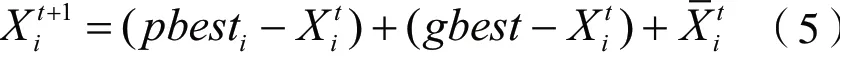
3 结论

研究工作在PSO算法基础上，以获取更合适的解决方案为目标设计了多种的优化改进策略，并应用于制造系统等相关领域。随着智能化技术的不断深入，所需算法的优化要不断成熟，因此，对未来的粒子群算法的重点得出如下结论：

（1）混合算法可以结合不同算法的优点，弥补单一算法的不足。随着粒子群算法在不同领域中的广泛应用，其与更多算法的混合会涉及更多新的领域，带动新领域的进展。

（2）多目标粒子群算法的基础研究和灵活性的拓展。由于多目标粒子群算法相关的数学理论还不够完备，算法的收敛性、多样性、迭代公式和参数等研究有待深入开展。在不同的优化阶段，需要算法的收敛和多样性也有所不同。如王学武， 薛立卡，顾幸生[26]在算法中同实引入三种突变因子，并用随机数来选择策略，以增加所得解的多样性。因此，算法在问题上的灵活调整机制不断优化需进一步探究。

（3）连续PSO和离散PSO的性能对比。PSO最初是解决连续问题提出的，但离散化对于数据的紧凑会更好。但连续PSO可通过映射的方法解决离散问题，所以它们的性能的对比和研究值得进一步探讨。如文献[23]通过求解FT06和FT10实例的最小使程值，比较了连续粒子群算法和离散粒子群算法的性能。