基于多粒度粗糙集与多级可拓的高速磁浮系统综合评判
邱乐侠,胡启洲,吴翊恺,吴啸宇
基于多粒度粗糙集与多级可拓的高速磁浮系统综合评判
邱乐侠,胡启洲,吴翊恺,吴啸宇
(南京理工大学,自动化学院,南京 210094)
以高速磁浮的设计理念、技术背景和应用场景为基础,利用包含多粒度粗糙集的多级可拓评价法对高速磁浮系统进行综合评判,直观反映高速磁浮系统的综合优良等级。首先从运行速度、舒适性、安全性、可靠性、经济性以及社会战略性6个角度对影响高速磁浮系统的因素进行分析,确立15个特征评判指标,并且建立高速磁浮系统的综合评判指标体系;其次利用层次分析法和多粒度粗糙集对高速磁浮不同评判指标进行综合赋权,弥补单一主观或客观赋权方法的不足;最后将多级可拓评价法以及模糊评价法分别运用到高速磁浮的系统综合评判中。理论分析和计算结果表明:高速磁浮系统的综合评判等级为“良好”。同时相较于模糊评价法,包含多粒度粗糙集的多级可拓评价法在高速磁浮系统综合评判中更加精确客观,有较好的可行性和实用前景。
高速磁浮;综合评判;多粒度粗糙集;多级可拓评价法
0 引 言
高速磁浮是高速磁悬浮列车的简称,是一种基于磁悬浮技术的高速铁路运输系统。与传统的轮轨高速铁路不同,它主要依靠常导磁吸或超导磁斥技术使列车在轨道上无接触行驶[1]。由于消除了轮轨摩擦,高速磁浮的运行时速可达600km/h以上,因此其具有填补轮轨高铁和民航飞机间速度断层的能力,为中长途旅客提供更多样化选择。德国工程师赫尔曼·肯佩尔(Hermann Kemper)于1922年提出了电磁浮原理[2],并开始研究其在轨道列车上的应用。随着经济与工业实力的增长,不少国家相继开始涉足磁浮运输系统的研究,并且取得重大发展。2009年6月,德国TR09型磁浮列车在埃姆斯兰试验线达到550km/h的运行速度;2015年4月,日本L0系超导磁浮列车在山梨试验线达到了最高603km/h的行驶速度;2019年5月,时速600km/h高速磁浮试验样车在青岛下线,标志中国在高速磁浮领域实现重大突破[3];2021年1月13日,由中国自主设计研发并制造的高温超导高速磁浮样车和试验线正式下线启用,其目标运行速度预计将大于620km/h[4]。
为实现高速以及超高速的磁悬浮轨道交通,需要解决一系列的关键技术难点,包括:牵引制动问题、动力热力学问题、安全问题、无线通信问题、车内环境控制问题等[5]。除此之外,作为一种未来将面向大众的高速轨道交通运输系统,针对高速磁浮舒适性、安全性、可靠性、经济性等方面的研究同样十分重要。在高速磁浮的舒适性方面:龚胤文等人[6]根据波动理论研究了高速磁浮舷窗的隔声性能,丁叁叁等人[7]则在预测评估高速磁浮沿线环境噪声后提出气动优化方案,焦齐柱等人[8]研究了高速磁浮通过隧道时产生的压力脉动对耳感舒适的影响。在高速磁浮的安全性方面,郑晓龙等人[9]研究了磁悬浮列车悬浮间隙波动对梁体刚度的影响;余宽原等人[10]研究了磁浮列车运行引起的环境微振动影响,高鹏等人[11]利用梯形模糊数理论对轨道交通体系中的供电设备进行了风险评估。而在社会发展方面,薛锋等人[12]利用灰色关联法研究了铁路客货运量对唐山社会经济系统的影响,殷勇等人[13]借鉴国外规划、法律、政策等方面的经验分析了国内城市群轨道交通的发展情况。
目前学者们对高速磁浮系统的研究大多集中在其物理特性与材料技术上,对高速磁浮的经济性、社会战略性等方面的综合分析较少。作为一种尚未进行大规模商业运营的公共交通系统,高速磁浮将承担吸纳客流、发展经济的任务,其舒适性、经济性和社会战略性影响会对其本身技术研究发展起到指导性作用,因此针对其多方面的科学综合评判十分必要。参考高速铁路评价方法与指标体系,构建高速磁浮系统综合评判模型,利用多粒度粗糙集与多级可拓评价法进行计算,并与模糊评价法进行对比。结果表明,基于该方法的高速磁浮系统综合评判能为高速磁浮的特征评判提供科学依据,同时对我国研究发展并推广高速磁浮交通系统起到一定指导意义。文章的结构流程如图1所示。

图1 文章结构流程
1 高速磁浮系统综合评判指标体系
高速磁浮的系统综合评判体系主要服务于旅客以及铁路部门,影响高速磁浮系统的因素众多,不同的子系统之间也会互相影响。由于指标体系合理性直接影响系统综合评判等级,应当从综合性、系统性、科学性原则出发,尽可能全面客观地反映出影响高速磁浮系统综合评判的主要因素。
首先,作为特殊的高速铁路运输系统,运行速度是其系统评价中的关键指标;其次,高速磁浮需要吸纳轮轨高铁与民航飞机的客流需求,舒适性指标不可或缺,包括运行平稳性、车内噪声控制、车站换乘便捷性等;此外,高速磁浮作为陆上最快的交通工具,安全与可靠性指标也是重中之重;最后,研究并推广运营高速磁浮还需考虑经济性与社会性因素,除了成本能耗收益之外,还包括其对都市圈经济的影响,对环境的影响(例如车外噪声污染、电磁辐射污染等),以及其对发展相关技术材料的影响(例如高速电磁直线驱动、高温超导材料技术等[14, 15])。
根据上述指标选取原则,以速度、舒适性、安全性、可靠性、经济性和社会战略性6个方面为一级指标B(= 1, 2, …, 6),同时相应选取15个二级指标C(= 1, 2, …, 15),如图2所示,构建包括目标层、准则层、指标层在内的高速磁浮系统综合评判指标体系。

图2 高速磁浮系统综合评判指标体系
在综合评判中将等级划为5等,专家按十分制法打分,打分的分值按大小与评判等级对应。考虑后续计算出现小数的情况,令最高等级的得分要求最严格,故设各等级界定区间如表1所示。

表1 高速磁浮系统综合评判等级界定区间
2 基于多粒度粗糙集的指标权重界定模型
权重可以体现不同指标在分析判断过程中的重要程度。为实现针对高速磁浮系统的综合评判,在构建其指标体系之后,需要一种合理有效的方法来确定各指标权重。针对图2所示的指标体系,根据多粒度粗糙集理论,可计算出评判指标的主客观综合赋权结果,其流程如图3所示。

图3 评判指标主客观综合赋权流程
2.1 高速磁浮系统的多粒度粗糙集模型
粗糙集理论由波兰学者Z. Pawlak[16]教授于1982年提出,是一种能够有效处理信息系统中不精确和不完整信息的数学分析方法。粗糙集理论可以对信息系统中的数据进行分析和推理,并从中发现隐含信息和潜在规律。凭借这种优势,粗糙集理论在属性约简[17, 18]、规则推导[19]、数据挖掘[20, 21]等方面都得到广泛研究和应用。由于粗糙集理论不需要为其提供问题所需数据集合之外的先验信息,这种优势驱使人们尝试将粗糙集理论应用到决策问题的权重赋值中去。
1996年,Zadeh[22]首次提出并讨论模糊信息的粒化问题。钱宇华等人[23-25]通过研究粗糙集理论与粒计算之间的关联,分析了单一粒度空间下粗糙集的不足,提出多粒度粗糙集的概念。在目前的多粒度粗糙集研究中,往往利用粒度权重对决策问题中的指标进行赋权。利用多粒度粗糙集的概念,对高速磁浮系统做出如下定义:
定义1[26]将高速磁浮系统定义为四元组决策信息系统=(,∪,,),其中论域表示高速磁浮系统非空有限全体对象集,条件属性集表示高速磁浮系统评判指标C的集合,为高速磁浮系统决策属性集,为高速磁浮系统全体属性值域集,为系统中×(∪)→的信息函数。
定义2[27]将高速磁浮的决策信息系统(DIS)上的不可区分关系()定义为:

高速磁浮系统的不可区分关系()相当于其论域上的一个等价关系,而()在上导出的划分记作/(),也可简记为/。论域元素在高速磁浮系统条件属性集下的等价类[]为:

同时根据粒度计算的观点,等价关系()即对应一个粒度,上的划分/()=[]就对应了一个粒结构,因此等价类[]即可被称为高速磁浮系统上关于条件属性集的知识粒。
定义3[28]在高速磁浮的决策信息系统中,设非空有限对象集合为论域的子集,则集合关于二级评判指标C条件属性集的下近似集合与上近似集合分别为:


定义4[29]在高速磁浮的决策信息系统中,设决策属性集在论域上的划分/为{1,2, …,Y, …,},则高速磁浮系统条件属性集在决策属性集下的信息量为:

定义5[29]在高速磁浮的决策信息系统中,设剔除评判指标即粒度C后的粒度集为-C,其在决策属性集下信息量为(-C/),则粒度集中粒度C的信息重要度,即条件属性集中二级评判指标C的信息重要度(C,)为:
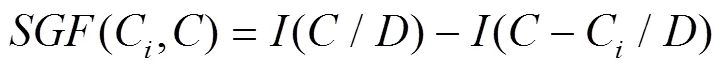
定义6[27]在高速磁浮决策信息系统中,根据粒度C的信息重要度,将粒度集的核,即二级评判指标C中的核粒度()定义为:

定义7[29]在高速磁浮决策信息系统中,设评判指标即粒度C在论域上划分/C为{1,2, …,Z, …,Z},则决策属性集相对于各粒度C的条件熵(/C)为:

2.2 指标权重的主客观综合界定
由于粒度信息重要度的计算方法只考虑了属性集合中各单一属性的重要度,容易出现某些粒度信息属性重要度为0的情况,故引入粒度条件熵,将其与粒度信息重要度求和并进行归一化处理,进而获得各粒度的客观赋权结果(C),如下式所示:

为了提高指标权重计算结果的科学性与合理性,需要将主客观的指标权重界定方法综合起来。参考设置一个系数,根据公式(7)所示的多粒度粗糙集核理论,对系数作如下定义:

在主客观综合赋权中,常取两种权重的均值作为最终结果,而系数则在此基础上体现粒度集中核粒度与非核粒度间比例对客观权重占比的影响。当粒度集中均为核粒度或非核粒度时,= 0.5;当粒度集中核粒度与非核粒度间比例为1时,= 0。由此可得,∈[0,0.5]。
设高速磁浮系统二级评判指标的主观赋权结果为(C)。为了体现客观赋权的主导性,则可根据二级评判指标的客观赋权结果(C)以及系数,将主客观综合赋权结果(C)定义为:

3 高速磁浮系统综合评判
交通领域的评价方法众多,包括模糊评价法、灰色关联系数法、价值函数法等。模糊评价基于决策过程的模糊性特点,通过隶属度理论得到评价结果,但在指标过多的条件下会导致超模糊问题;灰色关联系数法基于指标发展趋势,通过曲线近似度得到指标间数值关系,但不易确定正负相关性;价值函数法基于指标权重与系统价值,通过加权计算得到综合指标,但不易确定各个单项指标权重。
利用层次分析法和多粒度粗糙集计算指标权重,采用多级可拓法对高速磁浮系统进行特征评判,系统且全面地分析处理评价数据,并解决评判指标中存在的不确定性问题。与模糊评价法进行对比,分析两者评判过程与结果,研究多级可拓法在高速磁浮系统综合评判中的优势,流程如图4所示。

图4 高速磁浮系统综合评判流程
3.1 基于模糊评价的高速磁浮系统综合评判
基于模糊数学理论,模糊评价法可将定性评价转化为定量评价,对受多种因素影响的系统做出综合性评价。模糊评价法的优势在于其较强的系统性,能较好处理系统评价中部分难以量化的问题,适合各种包含非确定性指标的评价问题。模糊评价的步骤如下所示:
Step1 利用层次分析法和多粒度粗糙集计算15个指标的权重系数,得到指标权重矩阵。
Step2 针对高速磁浮的系统特征,如表1所示,采用十分制方法划分五个评判等级区间。
Step3 根据专家打分的比例计算各指标关于各等级的隶属度,进而得出模糊关系矩阵。
Step4 计算模糊综合评判矩阵=·,依据最大隶属度确定高速磁浮系统的最终评判等级。
3.2 基于多级可拓的高速磁浮系统综合评判
可拓学理论由蔡文等人[30]于1983年提出,是一种用以解决多参数混合且不相容问题的理论方法。可拓学理论通过形式化的计算方法,从定性和定量的角度研究分析复杂问题的规律以及解决方法。假设高速磁浮系统为待评判的系统,系统中物元以三元组= (,,)表示。其中为待评判事物,代表待评判事物的评判指标(即条件属性集),代表相应的指标等级值(即属性值域集)。若有多个评判指标,则称相应物元为多维物元。
3.2.1 高速磁浮系统的经典域、节域与待评物元
用参数(= 1, 2, 3, 4, 5)表示高速磁浮系统及其指标的评判等级,N则表示在评判等级下高速磁浮系统及其指标的评判效果。二级评判指标C关于评判效果N的取值域S为(a,b),即各评判等级关于相应评判指标的数据范围经典域。根据上述定义,对应的三元组如下式所示:

用N表示所有的评判等级,二级评判指标C关于全体评判等级N的取值范围S为(a,b),即所有评判等级关于相应评判指标的数据范围节域,则对应的三元组如下式所示:

式中,且S包含S。
调查或统计相关评判指标的数据,用物元(B)表示高速磁浮系统的综合评判,如下式所示:

式中,V表示高速磁浮系统综合评判中二级评判指标C的实际取值,且V∈S。
3.2.2 高速磁浮系统的评判指标关联函数
在多级可拓评价计算的过程中,需要计算各个评判指标与各个评判等级之间的关联度,相应的关联函数如下式所示:

式中,K(C)表示二级评判指标C关于评判等级的关联度。
公式(15)中(V,S)与(V,S)分别表示评判指标C的实际取值V与取值范围(a,b)以及(a,b)之间的距。
计算一个实际取值与取值范围(,)之间距的公式如下所示:

3.2.3 高速磁浮的多级可拓评价
在一级指标B下,根据下属二级指标C的相对权重(C)以及其关于等级的关联度K(C),相乘求和计算出一级指标B关于等级的关联度K(B),如下式所示:

根据各一级评判指标的计算权值(B),以及各一级评判指标B关于各评判等级的关联度K(B),相乘求和计算出高速磁浮系统关于各个评判等级的关联度K(),如下式所示:

当高速磁浮系统关于评判等级的关联度K′()满足式(19)时,即可认为其评判等级为′等级:

此时根据公式(20)的定义,即可利用公式(21)计算得出高速磁浮系统的级别变量特征值*:

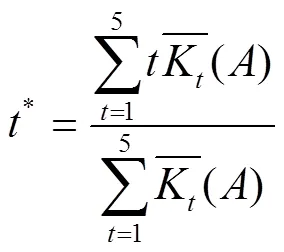
式中,计算评判等级′以及级别变量特征值*的方法同样适用于对评判指标C和B的等级判断。
4 算例分析
在高速磁浮决策信息系统中,条件属性集为所有二级指标C的集合,决策属性集是针对高速磁浮系统的整体性评价,而论域为各位打分专家的集合(1,2, …,20)。各位专家对所有二级评判指标C和高速磁浮系统整体性评价的打分如表2所示。

表2 高速磁浮系统综合评判指标打分
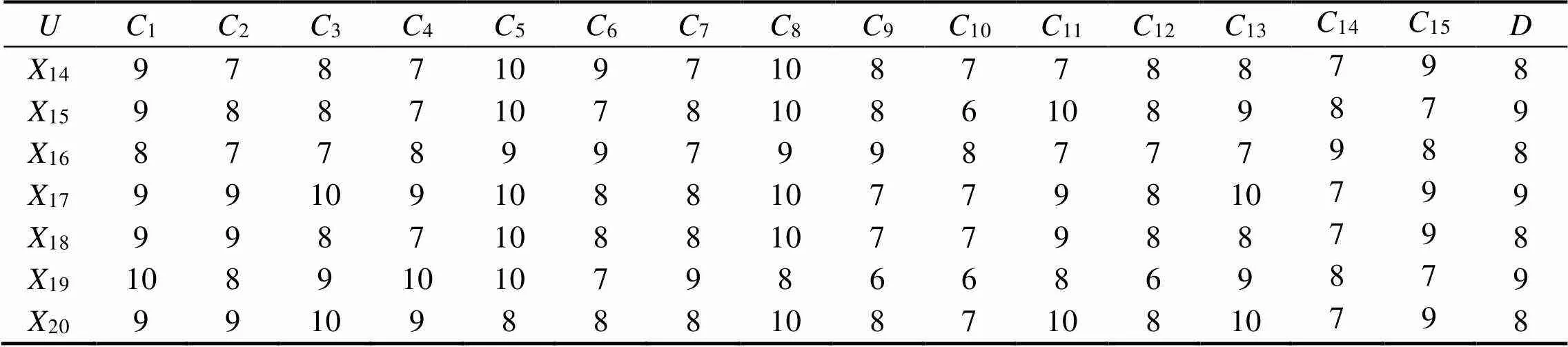
续表2
4.1 评判指标权重主观界定
根据图2指标体系,用数值平均法集结 所有专家的层次分析结果,得到一级与二级评判指标的主观赋权值(m)、(i),结果如表3所示。其中,所有原始判断矩阵均符合一致性检验要求。

表3 基于层次分析法的指标主观赋权
4.2 评判指标权重客观界定
根据表2与定义2计算系统总体得分在论域上的划分,即粒结构/,结果如下所示:
同样,根据定义2计算评判指标C在论域上的划分,即粒结构/C,结果如下所示:
根据定义3计算粒结构/中知识粒1与2关于各评判指标C的下近似集,结果如下所示:
根据公式(5)计算粒度集以及粒度集-C在决策属性集下的信息量,结果如表4所示。

表4 信息量I(C/D)及I(C-Ci/D)计算结果
根据公式(6)和(7),高速磁浮系统中条件属性集的核为{1,4,5,11,13},其信息重要度(C,)分别为0.0150、0.0075、0.0075、0.0075、0.0075,而其余非核粒度的信息重要度则为0。
根据公式(8)计算决策属性集相对于各粒度C的条件熵,结果如表5所示。

表5 粒度条件熵H(D/Ci)计算结果
根据公式(9)将信息重要度与条件熵求和并归一化,计算各粒度权重(C),结果如表6所示。

表6 基于多粒度粗糙集的指标客观赋权
4.3 评判指标权重主客观综合界定
根据公式(10)可得=0.1667,代入公式(11)得到指标综合赋权值(B)、(C),结果如表7所示。

表7 高速磁浮系统综合评判指标主客观综合赋权
4.4 基于模糊评价的高速磁浮系统综合评判
模糊综合评判矩阵的计算公式为=·。其中,指标权重矩阵可从表7综合赋权结果中得出,模糊关系矩阵可根据专家打分情况和等级区间得出。模糊综合评判矩阵的计算结果如下所示:

依据最大隶属度,可以确定高速磁浮系统的最终评判等级为1级“优秀”。
4.5 基于多级可拓的高速磁浮系统综合评判
根据等级区间,用公式(12)和(13)确定经典域与节域。以一级评判指标1为例,结果如下所示:

取20份数据均值作为指标实际取值V,根据公式(14)可得一级指标待评物元(B)如下所示:
在此基础上,根据公式(15)和(16)计算指标C关于评判等级的关联度K(C),结果如表8所示。

表8 二级评判指标Ci的等级关联度Kt(Ci)
根据公式(17)计算各个一级评判指标B关于评判等级的关联度K(B),结果如表9所示。

表9 一级评判指标Bm的等级关联度Kt(Bm)
根据公式(18)计算高速磁浮系统综合评判关于评判等级的关联度K(),结果如表10所示。同时根据公式(20)和(21),计算可得其级别变量特征值*=1.890 3。

表10 高速磁浮系统综合评判等级
4.6 评判结果对比分析
基于模糊评价的高速磁浮系统综合评判为1级“优秀”,而基于多级可拓的结果为2级“良好”。同时由于*=1.890 3,表明多级可拓评价的结果在1级与2级之间,并且更加倾向于2级“良好”。
两种评价方法的不同结果主要源于其处理指标时的精度差异。以指标10为例,根据表1和表2,其模糊隶属度为[0,0.55,0.45,0,0],模糊等级为2级“良好”;而由表8可知,其在多级可拓评价中为3级“中等”。这是由于模糊评价仅简单统计相应等级区间内的打分数量比例,虽然直观反映了专家对指标等级的定性判断,却忽视了数据中的定量内容。而多级可拓评价法还计算了指标与等级区间之间的距,进一步挖掘了打分数据中的定量信息。两种评价方法的特点比较如表11所示。

表11 模糊评价法与多级可拓评价法比较
此外,根据表2可得高速磁浮系统整体性打分的平均值为8.5。类比公式(15)和(16),可知其等级关联度K()如表12所示。并且类比公式(20)和(21),可知其级别变量特征值*= 1.959 6,与多级可拓的评价结果近似。可见在高速磁浮系统综合评判中,多级可拓评价相较于模糊评价有更好的适用性。
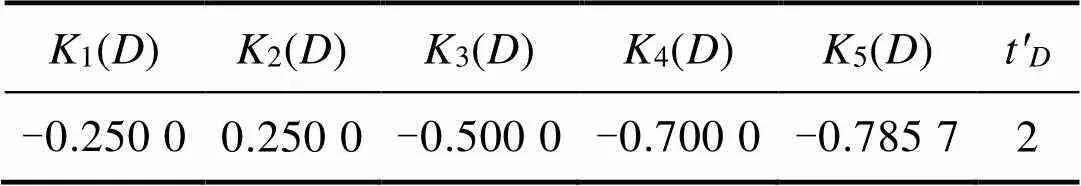
表12 整体性指标D的等级关联度Kt(D)
5 结 语
本文从高速磁浮技术特征和应用前景出发,综合考虑速度、舒适性、安全性、可靠性、经济性、社会战略性6方面因素,构建高速磁浮系统综合评判指标体系。在权重计算方面,综合层次分析法与多粒度粗糙集,对15个指标进行主客观综合赋权,考虑了数据客观性也兼顾了主观经验重要性;在利用多粒度粗糙集计算客观权重时,引入粒度条件熵的概念,弥补单一粒度信息重要度的不足。
本文采用多级可拓评价法对高速磁浮系统进行综合评判,结果表明,相较于模糊评价法,多级可拓评价结果(′ = 2,*= 1.890 3)与系统整体性打分(′= 2,*= 1.959 6)更接近,说明该方法在高速磁浮系统的综合评判中更具适用性,能够为高速磁浮系统发展提供参考。
本文研究也有不足之处,如由于高速磁浮系统尚未运营,无法获得平稳性、安全性等指标数据,因此分析结果有一定主观偏差。在未来应进一步分析高速磁浮的实际数据,使研究更具实际意义。
[1] 程建峰, 苏晓峰. 磁悬浮列车的发展及应用[J]. 铁道车辆, 2003, 41(11): 14-17, 1.
[2] 江浩, 连级三. 磁悬浮列车在世界上的发展与展望[J]. 铁道学报, 1991(2): 95-101.
[3] 余浩伟, 寇峻瑜, 李艳. 600 km/h高速磁浮在国内的适应性及工程化发展[J]. 铁道工程学报, 2020, 37(12): 16-20, 88.
[4] 熊嘉阳, 邓自刚. 高速磁悬浮轨道交通研究进展[J]. 交通运输工程学报, 2021, 21(1): 177-198.
[5] YOSHIOK A H, SUZUKI E, SEINO H, et al. Characteristics of the dynamic of the MLX01 yamanashi maglev test line vehicles[J]. Railway Technical Research Institute Quarterly Reports, 1998, 39(2): 62-67.
[6] 龚胤文, 葛剑敏. 基于波动理论的高速磁浮列车舷窗隔声性能[J]. 华中科技大学学报(自然科学版), 2020, 48(6): 57-63.
[7] 丁叁叁, 葛剑敏, 郭建强, 等. 高速磁浮系统噪声排放评估及应对措施[J]. 机车电传动, 2020(6): 6-9.
[8] 焦齐柱, 肖明清, 周俊超, 等. 基于乘员耳感舒适性的时速600 km磁悬浮单线隧道最优净空面积研究[J]. 铁道科学与工程学报, 2020, 17(12): 2993-3002.
[9] 郑晓龙, 陈星宇, 徐昕宇, 等. 某磁浮大跨斜拉桥竖向刚度限值研究[J]. 中国铁道科学, 2021, 42(01): 43-48.
[10] 余宽原, 顾晓强, 黄茂松, 等. 磁悬浮列车运行引起的环境微振动实测分析[J]. 岩土工程学报, 2020, 42(S1): 146-150.
[11] 高鹏, 唐昭, 杨坤洪, 等. 城市轨道交通运营设备安全风险评价[J]. 交通运输工程与信息学报, 2020, 18(1): 91-98.
[12] 薛锋, 徐莉. 唐山市铁路客货运量对区域社会经济系统的影响分析[J]. 交通运输工程与信息学报, 2020, 18(2): 75-82.
[13] 殷勇, 鞠子奇, 吴雨遥, 等. 国外轨道交通发展对我国城市群轨道交通一体化的启示[J]. 交通运输工程与信息学报, 2021, 19(1): 52-58.
[14] WANG J S, WANG S Y, ZENG Y W, et al. The first man-loading high temperature superconducting maglev test vehicle in the world[J]. Physical C: Super Conductivity and Its Applications, 2002, 378(1): 809-814.
[15] 沈志云. 关于我国发展真空管道高速交通的思考[J]. 西南交通大学学报, 2005(2): 133-137.
[16] PAWLAK Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11: 341-356.
[17] JIA X Y, LIAO W H, TANG Z M, et al. Minimum cost attribute reduction in decision-theoretic rough set models[J]. Information Sciences, 2013, 219: 151-167.
[18] ZHANG Y M, JIA X Y, TANG Z M. Minimum cost attribute reduction in incomplete systems under decision- theoretic rough set model[C]// 2016 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery(ICNC-FSKD). Changsha: 2016: 940-944.
[19] JAROSLAW B, ALEKSANDRA R Z, PAWEL Z. Rough set theory in the classification of loan applications[J]. Procedia Computer Science, 2020, 176: 3235-3244.
[20] DAI J H, TIAN H W, WANG W T, et al. Decision rule mining using classification consistency rate[J]. Knowledge- Based Systems, 2013, 43: 95-102.
[21] JIA X Y, LI W W, SHANG L. A multiphase cost-sensitive learning method based on the multiclass three-way decision- theoretic rough set model[J]. Information Sciences, 2019, 485: 248-262.
[22] ZADEH L A. Fuzzy sets and information granularity[C]// Advances in Fuzzy Set Theory and Application, 1996: 3-18.
[23] QIAN Y H, LIANG J Y. Rough Set Method Based on Multi-Granulations[C]// 2006 5th IEEE International Conference on Cognitive Informatics, Beijing: IEEE 2006: 297-304.
[24] QIAN Y H, LIANG J Y, DANG C Y. Incomplete Multigranulation Rough Set[C]// IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 2010: 420-431.
[25] QIAN Y H, LI S Y, LIANG J Y, et al. Pessimistic rough set based decisions: A multigranulation fusion strategy[J]. Information Sciences, 2014, 264: 196-210.
[26] 张明, 程科, 杨习贝, 等. 基于加权粒度的多粒度粗糙集[J]. 控制与决策, 2015, 30(2): 222-228.
[27] 彭连贵, 阎瑞霞, 陈昭君. 多粒度粗糙集粒度权重确定的综合方法[J]. 计算机应用研究, 2019, 36(11): 3250-3252, 3268.
[28] 孟慧丽, 马媛媛, 徐久成. 基于信息量的悲观多粒度粗糙集粒度约简[J]. 南京大学学报(自然科学版), 2015, 51(2): 343-348.
[29] 黄卫华. 多粒度粗糙集模型[J]. 西南师范大学学报(自然科学版), 2017, 42(5): 137-143.
[30] 蔡文, 杨春燕, 林伟初. 可拓工程方法[M]. 北京: 科学出版社, 1997: 15-18.
Comprehensive Evaluation of a High-speed Maglev System Based on Multi-granularity Rough Set and Multi-level Theory of Extension
QIU Le-xia, HU Qi-zhou, WU Yi-kai, WU Xiao-yu
(School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China)
Based on the design concept, technical background, and application prospect of a high-speed maglev, its system characteristics are evaluated comprehensively by using the multi-level theory of extension including a multi-granularity rough set to reflect its comprehensive grade more intuitively. First, the factors affecting the system characteristics of the high-speed maglev are analyzed from the aspects of speed, comfort, safety, reliability, business economics, and social strategy; 15 characteristic evaluation indexes are proposed and a comprehensive evaluation index system is established. Second, the weight of different evaluation indexes for the high-speed maglev is calculated by using the analytic hierarchy process and the multi- granularity rough set, which can compensate for the shortcomings of the subjective or objective single-weighting method. Finally, the multi-level theory of extension and the fuzzy evaluation theory are, respectively, applied to the comprehensive evaluation of the high-speed maglev system. Theoretical analysis and calculation results demonstrate that the comprehensive evaluation grade of the high-speed maglev is “good”. Meanwhile, compared with fuzzy evaluation theory, the multi-level theory of extension including a multi-granularity rough set is more accurate and objective in comprehensive evaluation of a high-speed maglev system, and it has better feasibility and practicability.
high-speed maglev; comprehensive evaluation; multi-granularity rough set; multi-level theory of extension
U237
A
10.19961/j.cnki.1672-4747.2021.04.0002
1672-4747(2021)04-0106-12
2021-04-01
2021-05-23
2021-05-26
2021-04-01~04-06;05-12~05-21;05-23
国家自然科学基金项目(51178157);江苏省“六大人才高峰”高层次人才项目(JXQC-021);河南省重点科技攻关项目(182102310004);教育部人文社科科学研究项目(18YJAZH028)
邱乐侠(1996—),男,硕士研究生,研究方向:轨道管理安全,E-mail:qiulexia1015@163.com
邱乐侠,胡启洲,吴翊恺,等. 基于多粒度粗糙集与多级可拓的高速磁浮系统综合评判[J]. 交通运输工程与信息学报,2021, 19(4): 106-117.
QIU Le-xia, HU Qi-zhou, WU Yi-kai, et al. Comprehensive Evaluation of a High-speed Maglev System Based on Multi-granularity Rough Set and Multi-level Theory of Extension[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 106-117.
(责任编辑:刘娉婷)

