基于复杂网络的国家综合立体交通网主骨架分析
张勤宇,帅 斌,吕 敏
基于复杂网络的国家综合立体交通网主骨架分析
张勤宇,帅 斌,吕 敏
(西南交通大学,交通运输与物流学院,成都 611756)
《国家综合立体交通网规划纲要》中提出要加快建设高效率国家综合立体交通网主骨架。本文借助复杂网络相关理论,以L空间方法构建了国家综合立体交通网主骨架区域网络与城市网络,分析了区域与城市之间的连接情况。结果表明:在由21个重点区域构成的区域网络中,每个重点区域与其他区域至少有2条路径相连接,且区域网络具有小世界的特点,说明重点区域之间连接紧密,可靠性强。在由116个节点构成的城市网络中,城市间连边以极、组群、组团等不同类型重点区域城市之间的连边为主;在考虑城市空间距离的加权网络中,重庆、西安等节点重要度较高,建议重点关注各种交通方式在这些节点的相互衔接情况以提升运输效率。在鲁棒性分析中,发现加权网络对随机攻击和基于接近度中心性的蓄意攻击鲁棒性较好,而对基于介数中心性和PageRank中心性的蓄意攻击鲁棒性较差。通过对主骨架的网络特性进行分析并识别其重要节点,本文研究结果不仅证实了主骨架规划的合理性,还可为重点区域及城市的综合交通运输规划提供其连接情况、支撑作用与拓扑重要性等理论层面的参考。
综合运输;交通规划;复杂网络;主骨架;立体交通
0 引 言
2021年2月24日,由中共中央、国务院印发的《国家综合立体交通网规划纲要》(以下简称“规划纲要”)对外公布。规划纲要提出,至2035年,我国将基本建成便捷顺畅、经济高效、绿色集约、智能先进、安全可靠的现代化高质量国家综合立体交通网。其中,综合立体交通网主骨架是其最关键、最高效、最主要的构成。依据交通运输的需求大小,划定4个极、8个组群与9个组团:将京津冀、长三角、粤港澳大湾区与成渝地区双城经济圈确立为4个极;将长江中游、山东半岛、海峡西岸、中原、哈长、辽中南、北部湾、关中平原等城市群确立为8个组群;将呼包鄂榆、黔中、滇中、山西中部盆地、天山北坡、兰州—西宁、宁夏沿黄、拉萨、喀什等城市群或城市圈确立为9个组团。规划纲要提出,要加快构建6条连接极与极的主轴,7条连接极与组群或组团的走廊,8条连接组群或组团与组团的通道,其基本情况如表1所示。

表1 国家综合立体交通网主骨架概况

续表1
注:括号内为支线涉及的组群或组团。
复杂网络理论是适用于研究人或事物之间联系的科学。近年来,复杂网络在交通运输领域研究中的应用较为广泛。Liu等[1]构建了地铁—高铁复合网络模型,以综合两者的轨道交通网络中的门到门时间为基础,通过算例验证分析该网络随时间变化的可达性与脆弱性。在城市公共交通方面,沈犁等[2]构建成都市地铁—公交复合网络模型,除分析其静态抗毁性之外,还基于运输能力和客流OD分析各条地铁线路失效情况下的拥堵传播情况。张琳等[3]基于ArcGIS缓冲区分析构建站点耦合识别后的常规公交—地铁复合网络,采用复合网络有效性与最大连通率进行网络脆弱性度量,并以南京市区为例对比分析耦合与非耦合网络在随机或蓄意攻击下的脆弱性情况。刘杰[4]等提出容忍系数以衡量地铁车站间的可容忍路径数,以成都地铁网络为例构建加权网络,分析不同容忍系数下各个地铁车站及地铁网络的连通可靠性。
综合交通网络是引导、支撑、协调国民经济发展的关键。早在2005年,国家发改委交通运输司就成立了《综合交通网络布局规划研究》课题组[5],采用考虑交通流强度的方法进行国家综合交通网的规划布局,分各省市区进行客货运量的预测并借助Logit模型将客货运量分担至铁路、公路等交通方式上。研究成果于2007年底形成《综合交通网中长期发展规划》,规划了“五纵五横”综合运输大通道与42个全国性综合交通枢纽[6]。围绕京津冀地区,高天等[7]对这一区域的综合运输体系进行了层次划分,寻找存在的不足之处并为未来发展提供了思路。随着交通强国战略的提出,需要构建新的综合交通网络以实现“全国123出行交通圈”与“全球123快货物流圈”的目标。刘勇等[8]借鉴美国的经验,提出构建五个层次的“直线三角形”交通连接,确立国家综合立体交通网络的顶层设计。陈卓等[9]选取中国337个地级以上行政单元,分析城市间交通网络的现状与未来通达性,并提取网络的最小支撑树以得到城市间要素流动的骨干网络。
目前,将复杂网络理论与国家综合交通网络相结合分析的文献较少。本文从复杂网络的角度出发,在第1节介绍拓扑网络的构建方法与研究需要的主要指标;在第2节进行国家综合立体交通网主骨架的拓扑特性分析;在第3节进行国家综合立体交通网主骨架的鲁棒性分析;在第4节进行结论总结并对未来研究进行展望。
1 复杂网络构建与指标
1.1 复杂网络构建方法
将交通网络用复杂网络表示有多种方法,而其中最为直观的表示方法即为将不同的地点视为不同的节点,并在具有直接连接的相邻节点之间构建连边,这种方法被称为L空间方法[10]。本文采用这种方法,以便于分析国家综合立体交通网中各城市或城市群之间的连接情况。
1.2 主要指标介绍
对于复杂网络的分析,采取的常用指标有平均度、平均最短路径长度、聚类系数、中心性等[11]。
1.2.1 平均度
节点的度为网络中连接至节点的边的数量,平均度为网络中所有节点的度的平均值。平均度反映了网络中节点与其他节点之间的连接情况。
1.2.2 平均最短路径长度
平均最短路径长度为网络中任意两个节点之间的最短路径长度的算术平均值。在无权网络中,两个节点之间的最短路径长度为由一个节点至另一个节点所经过的边的数量;而在加权网络中,最短路径长度为一个节点至另一个节点的路径上各边权值之和的最小值。
1.2.3 聚类系数
节点的聚类系数为节点的邻居节点之间实际存在的边数与总可能边数之间的比值,网络的聚类系数为网络图中所有节点聚类系数的算术平均值。
1.2.4 中心性
常用的中心性有度中心性、接近度中心性、介数中心性、特征向量中心性与PageRank中心性等。度中心性即为节点的度值。接近度中心性为某个节点至其他节点距离之和的倒数乘以其他节点个数。接近度中心性越高的节点越接近于网络的中心位置。介数中心性为网络中各个节点之间的最短路径通过某个节点的比例。介数中心性越高的节点,通过其最短路径数量就越多,连接各节点的作用就更大。特征向量中心性是图的邻接矩阵最大特征值对应的特征向量,节点的中心性与其连接的节点中心性成正比。在此基础上,Brin和Page[12]提出了PageRank中心性,基于邻接矩阵并考虑节点随机访问的情况构造状态矩阵,将这一状态矩阵转置后,再类比特征向量中心性的方法,求解其最大特征值对应的归一化特征向量,即为PageRank中心性。由于这一方法较好地过滤了质量较低的页面,因此被用于为Google搜索引擎结果进行排序。
2 主骨架网络拓扑特性分析
2.1 区域网络分析
根据表1的内容,将4个极、8个组群与9个组团共21个重点区域视为节点,将连接这些重点区域的6条主轴、7条走廊及8条通道视为连边并去除重复边,构建无向无权网络如图1所示。

图1 国家综合立体交通网主骨架重点区域连接情况
由图1可以看出,所有节点中度最小的节点为喀什,它的度为2。这表明,在综合立体交通网主骨架中,每个重点区域与其他区域至少有2条相联系的路径,与《国家综合立体交通网2035年主要指标表》中的第8项指标,即重点区域多路径连接比率目标值95%以上是契合的。网络的平均度为4.476,平均最短路径长度为2.376,网络聚类系数为0.441,说明各区域之间联系所需经过的区域较少,区域之间相互连接紧密,具备小世界网络的特点[13]。
在网络中,长江中游城市群具有最高的度中心性与介数中心性。作为南北、东西走向的京津冀—粤港澳、长三角—成渝两条主轴交汇处,长江中游城市群虽然未被定义为极,但其位于长江经济带中部且具有通达性强、沟通全国各地的特点,仍然使得这一区域在主骨架中具有重要的地位。关中平原城市群具有最高的接近度中心性与特征向量中心性。关中平原城市群处于我国陆地领土中部,至其他重点区域的距离适中,且与其直接相连的重点区域通达度普遍较好。
2.2 城市网络分析
结合规划纲要对国家综合立体交通网主骨架布局的描述及国家综合立体交通网主骨架布局示意图,摘取出其中提到的109个城市与地点,并在此基础上根据实际布局情况增加精河、海口、日喀则、襄阳、榆林、张家界、龙岩等未提及的7座城市及部分城市之间的连接关系。由于本研究主要考虑陆上交通,故去除2条沿海海上路径。
以京津冀—长三角主轴为例,这一主轴有四条路径:路径1为北京经天津、沧州、青岛至杭州;路径2为北京经天津、沧州、济南、蚌埠至上海;路径3为北京经天津、潍坊、淮安至上海;路径4为天津港至上海港沿海海上路径。根据前三条路径可以得到城市之间的连接关系,并去除北京—天津—沧州之间的重复连边。依据实际布局情况,在蚌埠至上海的路径中增加南京;依据主骨架布局示意图,将潍坊、淮安与大陆桥走廊起点连云港相连接。对其他主轴、走廊与通道进行类似处理,得到的城市网络共拥有116个节点,192条边。
2.2.1 分层网络分析
按照极、组群、组团的分类,将116个节点分为3层。第一层为位于4个极范围内的北京、天津等27个节点;第二层为位于8个组群范围内的青岛、济南等32个节点;第三层为位于9个组团范围内及其他区域、边境节点,包括太原、延安等57个节点。绘制分层网络如图2所示。
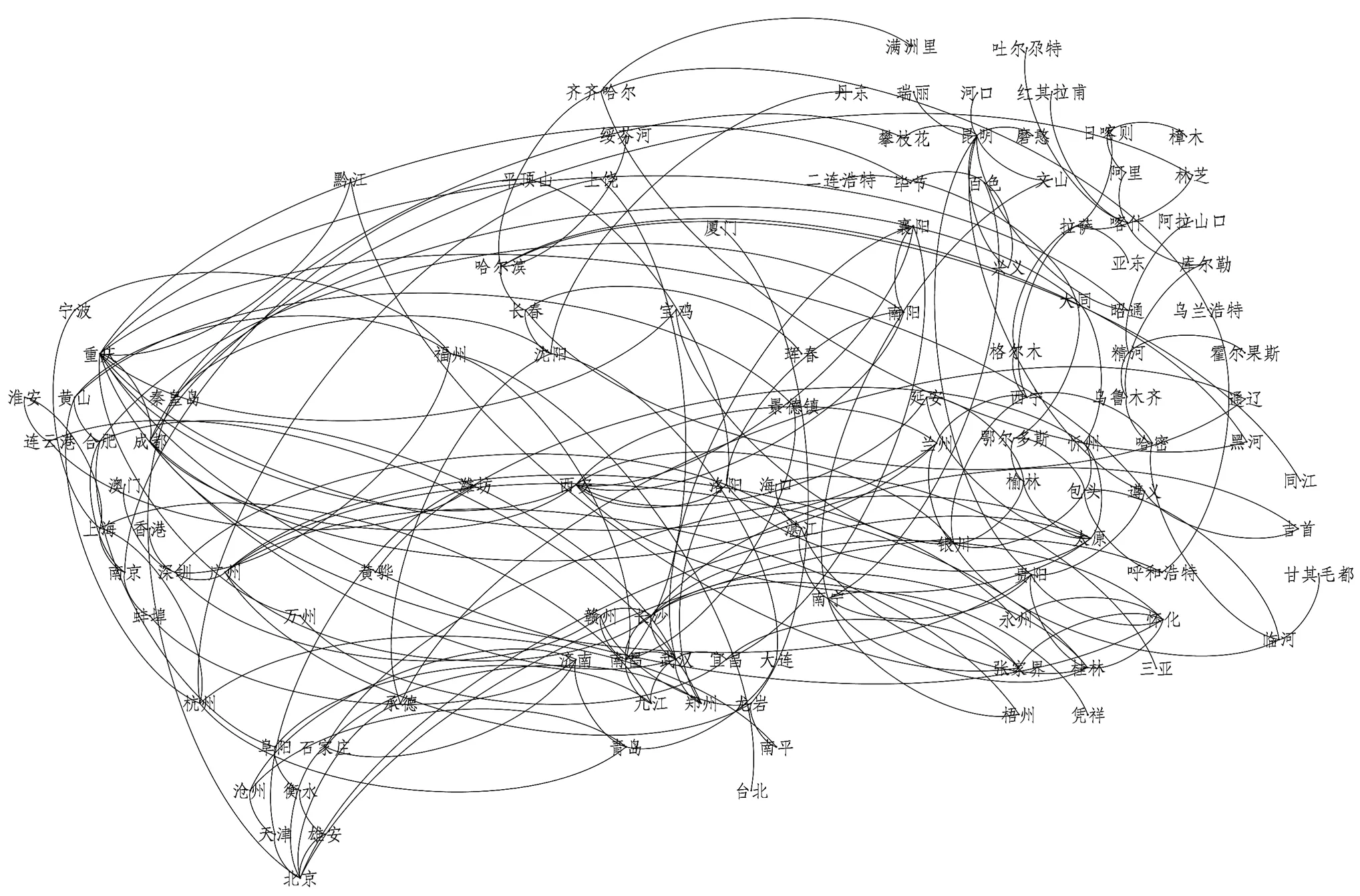
图2 国家综合立体交通网主骨架城市分层网络
由上图可以看出,综合立体交通网主骨架以不同网络层之间的层间连边为主,层内连边集中在第三层与第一层。第三层节点大多位于我国中西部地区,部分节点甚至位于主骨架中的末端区域,存在较多的末梢至组团中心连边,因此该层内联系较多。第一层节点位于4个最重要的极,极之间及极内部均存在大量的交通运输需求,需要一定的层内连边承担运输任务,支撑起交通网的骨架。第二层节点位于8个组群范围内,主要起到连接不同层节点的作用,层内节点之间的联系较少。
在各层节点中,节点度最大的节点依次为重庆、西安、昆明。重庆依托2条主轴、2条走廊与1条通道,与其直接相连的节点有11个,为整个网络中的最大值。与重庆直接相连的节点又处于连接其他重点区域的通道上,印证出重庆在交通网主骨架中的便捷性。西安亦具有与重庆相似的特点。与昆明直接连接的节点包含瑞丽、磨憨、河口等边境节点,分别连接缅甸、老挝、越南,有助于进一步深化与东南亚国家的多方面合作。
2.2.2 加权网络分析
在无向无权的城市网络的基础上,以连边的空间距离对网络进行加权。为简单起见,通过高德地图API(lbs.amap.com)提取各节点对应的当地行政中心经纬度,并导入ArcGIS软件获取相邻节点之间的直线距离作为边权重,构建无向加权网络,如图3所示。

图3 国家综合立体交通网主骨架城市网络
利用度中心性、接近度中心性、介数中心性和PageRank中心性这4个中心性指标,计算得到加权网络中各中心性排名前10的节点,结果如表2所示。
在加权城市网络中,接近度中心性较高的节点主要位于中部地区,如太原、洛阳、南阳、襄阳、宜昌、张家界均位于二湛通道上,说明该通道的建设可有效缩短中部地区城市至全国各地的时空距离。二湛通道北起重要国际运输口岸二连浩特,南至湛江,还可连接西部陆海走廊至三亚,为中部地区发展外向型经济提供交通支持。介数中心性排名较高的节点在网络中通常起到“桥梁”的作用,如重庆、北京、西安分别将西南、东北、西北地区与由主轴合围成的菱形区域紧密连在一起。在PageRank中心性中,西宁、喀什、哈密等入围前10名,表明这些节点在支撑国土空间开发与保护中具有重要地位。在主骨架网络构建过程中,建议关注中心性较高的节点的交通建设情况,在建设资源与资金分配等方面有所倾斜。
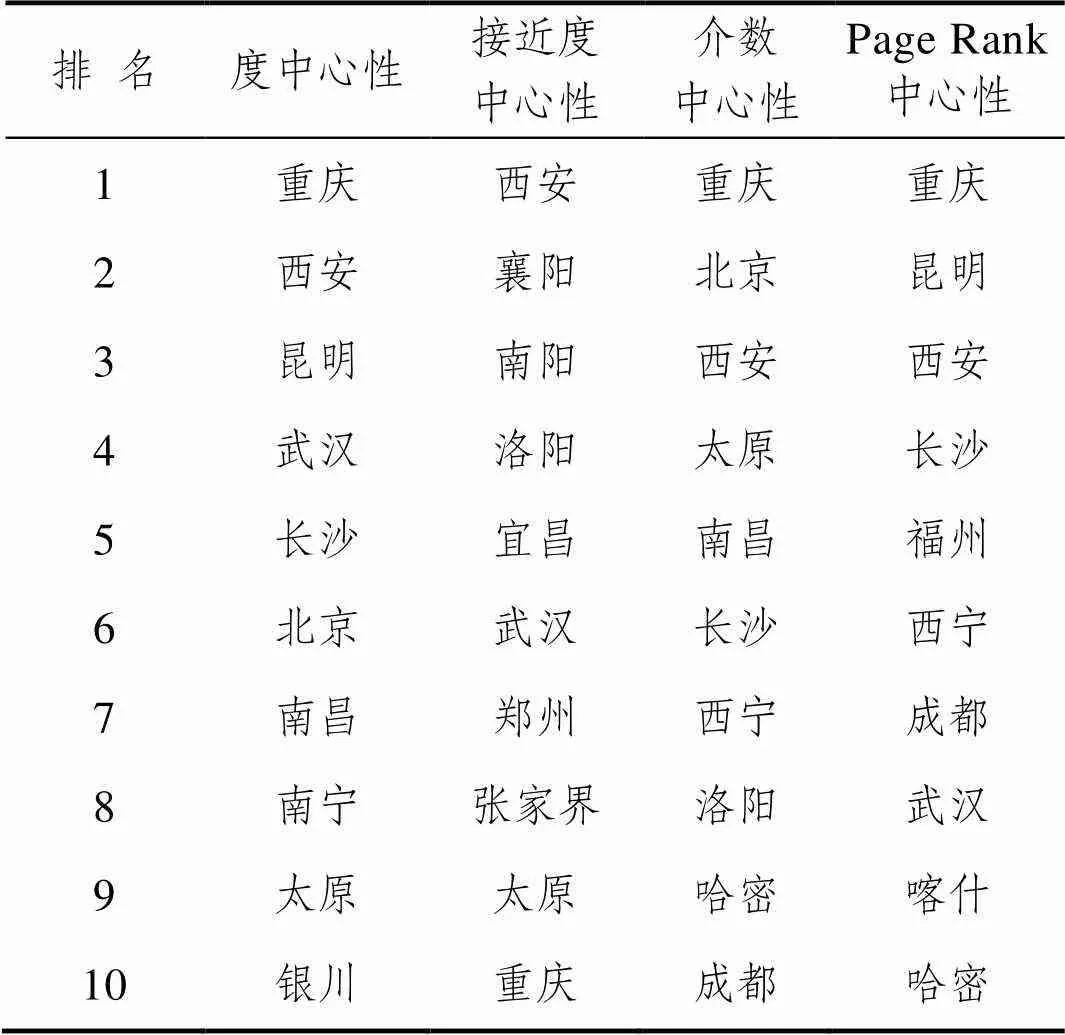
表2 主骨架城市网络中各中心性排名前10的节点
3 主骨架网络鲁棒性分析
国家综合立体交通网建成后可能会面临随机失效或蓄意攻击的情况。随机失效,例如受到台风、洪水等自然灾害的影响,而蓄意攻击则可能为遭受战争、恐怖袭击等极端情况。为此,对其进行鲁棒性分析是很有必要的。
本文选取主骨架城市加权网络进行鲁棒性分析。在随机失效中,随机选取节点进行移除;而在蓄意攻击中,根据接近度中心性、介数中心性与PageRank中心性的降序选择节点进行移除。在节点移除后,与节点相连的所有边均被移除。选取网络效率作为评价指标,网络效率为节点对之间距离倒数和的平均值,网络效率越高,说明节点间距离越短;反之,节点间距离越长甚至为无穷大,表示节点间互相不连通[14],其计算公式为:


对加权城市网络进行随机攻击与三种蓄意攻击,攻击结果如图4所示。其中,网络效率相对值为攻击节点之后的网络效率相对于初始网络效率的比值,相对值越低,说明网络效率越低。
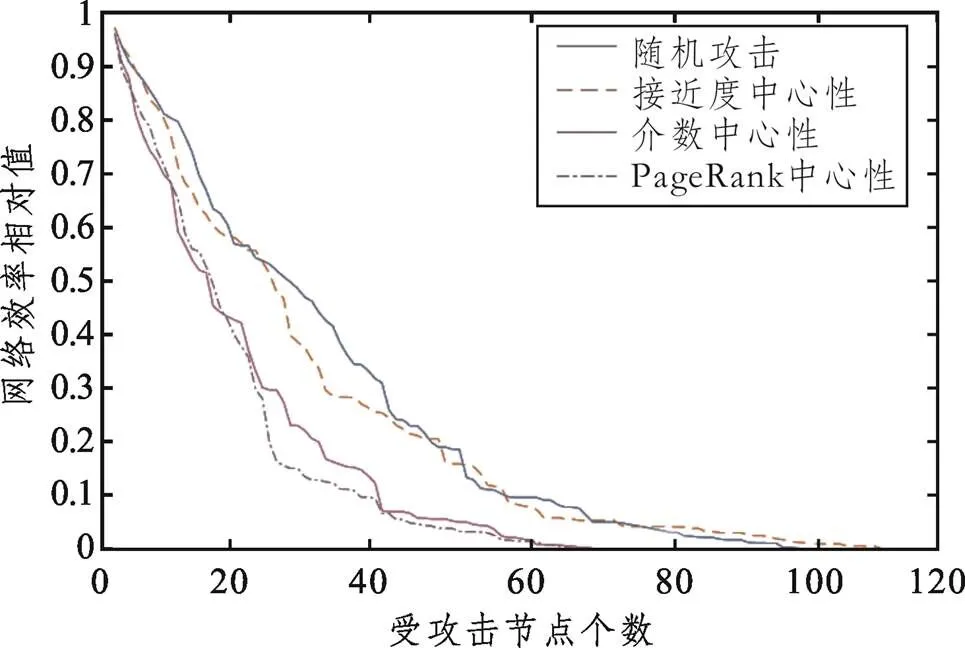
图4 主骨架网络在各种攻击下的网络效率相对值
由图4可以看出,立体交通主骨架网络面对随机攻击与基于接近度中心性的攻击展现出较强的鲁棒性,而面对基于介数或PageRank中心性攻击的鲁棒性较差。具体而言,在前20个节点遭到攻击失效后,随机攻击和基于接近度中心性的蓄意攻击的情况下,网络效率相对值仍在0.5以上;而基于介数或PageRank中心性的蓄意攻击令网络效率相对值下降到0.3左右,意味着网络已几近崩溃。
4 结束语
本文得到的主要结论如下:
(1)在由21个重点区域构成的区域网络中,分析各区域之间的联系与网络总体情况,可知主骨架网络中各区域之间连接紧密,网络具备小世界性。
(2)在由116个节点构建的城市分层网络中,以极、组群、组团的层间连边为主,层内连边主要出现在极层与组团层。在考虑空间距离的加权网络中,重庆、西安、昆明等节点中心性较高。就拓扑结构而言,中心性较高的节点在网络中的重要性较高。建议重视各种交通方式在这些节点的相互衔接情况以及这些节点的交通基础设施安全情况,以保证主骨架网络能够高效、稳定地运行。
(3)由116个节点构建的加权城市网络,面对随机攻击与基于接近度中心性的攻击展现出较强的鲁棒性,而面对基于介数和PageRank中心性攻击的鲁棒性较差。表明主骨架网络虽然在中部地区提供了较多的替代路径,但仍需加强对介数中心性和PageRank中心性较高的节点的保护。
规划纲要所提出的主骨架网络,在国家综合立体交通网中占有重要的地位。主骨架网络中每个重点区域与其他区域间均有2条及以上的路径相连接,且网络具备小世界性。这说明重点区域之间相互连接紧密,在自然灾害等特殊情况下仍可保障各重点区域的可达性。在面对随机攻击或基于接近度中心性的蓄意攻击时,主骨架网络也能展现出较强的鲁棒性,这表明即使接近度中心性较高的节点失效,主骨架网络中的其他节点与路径仍可以替代其运输功能。通过上述分析可以得知,主骨架网络弥补了现有交通体系中的短板,提升了交通网络的韧性,印证了规划纲要的合理性。
对城市网络进行分析,可以把握节点(城市)在主骨架网络中与其他节点之间的连接关系,在分层网络中可判断节点在网络中的支撑作用,在中心性分析中可从多个维度得知节点在网络中的拓扑重要性。这些都可以为重点区域及城市综合交通运输发展规划的编制提供理论层面的参考。在未来的研究中,可考虑不同交通方式的综合运力、运量等因素,使得研究突破拓扑层面,与运输实际相结合,更好地服务于综合立体交通网络的规划与建设。
[1] HONG L, OUYANG M, XU M, et al. Time-varied accessibility and vulnerability analysis of integrated metro and high-speed rail systems[J]. Reliability Engineering and System Safety, 2020, 193: 1-10.
[2] 沈犁, 张殿业, 向阳, 等. 城市地铁-公交复合网络抗毁性与级联失效仿真[J]. 西南交通大学学报, 2018, 53(1): 156-163, 196.
[3] 张琳, 陆建, 雷达. 基于复杂网络和空间信息嵌入的常规公交-地铁复合网络脆弱性分析[J]. 东南大学学报(自然科学版), 2019, 49(4): 773-780.
[4] 刘杰, 彭其渊, 陈锦渠, 等. 考虑乘客出行容忍度的城市轨道交通网络的连通可靠性分析[J]. 交通运输工程与信息学报, 2019, 17(4): 134-140.
[5] 国家发展改革委交通运输司《综合交通网络布局规划研究》课题组. 我国综合交通网络布局规划研究[J]. 综合运输. 2005(10): 4-6.
[6] 国家发展和改革委员会交通运输司. 综合交通网中长期发展规划[J]. 交通运输系统工程与信息, 2008, 8(1): 17-28.
[7] 高天, 王凯, 景岑芳. 京津冀综合交通运输体系发展研究[J]. 交通运输工程与信息学报, 2016, 14(3): 113-118.
[8] 刘勇, 魏际刚, 张立群. 国家综合立体交通网络建设的顶层设计[J]. 科技中国, 2021(1): 90-93.
[9] 陈卓, 梁宜, 金凤君. 基于陆路综合交通系统的中国城市网络通达性模拟及其对区域发展格局的影响[J]. 地理科学进展, 2021, 40(2): 183-193.
[10] FERBER C, HOLOVATCH T, HOLOVATCH Y, et al. Public transport networks: empirical analysis and modeling[J]. The European Physical Journal B, 2009, 68: 261-275.
[11] 孙玺菁, 司守奎. 复杂网络算法与应用[M]. 北京: 国防工业出版社, 2017.
[12] BRIN S, PAGE L, The anatomy of a large-scale hypertextual web search engine[J]. Computer Networks and ISDN Systems, 1998, 30(1): 107-117.
[13] WATTS D, STROGATZ S. Collective dynamics of “small-world” networks[J]. Nature, 1998, 393(4): 440-442.
[14] LÜ L Y, CHEN D B, REN X L, et al. Vital nodes identification in complex networks[J]. Physics Reports, 2016, 650: 1-63.
Analysis of the Basic Framework of the National Integrated Stereoscopic Transportation Network Based on Complex Network Theory
ZHANG Qin-yu, SHUAI Bin, LV Min
(School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China)
The planning outline has raised the issue of the procedure for constructing a high efficiency national integrated stereoscopic transportation network basic framework. This paper examined the basic framework of the region network and city network in L-Space, and used complex network theory to analyze the connections between regions and cities. The results are as follows. In the region network, each of the 21 important regions has at least two routes to other regions, and the network has a small-world property, indicating that the connections between important regions are close and reliable. In the city network with 116 nodes, the edges are mainly between cities in different important regions. In the distance-weighted network, nodes such as Chongqing and Xi’an have high centrality, and we advise that the interconnection between different means of transport at these nodes be specially concentrated to boost transportation efficiency. The robustness analysis showed that the weighted network is relatively robust under random attacks and malicious attacks based on closeness centrality, but performs worse under malicious attacks based on betweenness centrality or PageRank centrality. By analyzing the network properties and identifying the vital nodes of the basic framework, we not only demonstrate the rationality of the basic framework, but also provide a theoretical discussion of such issues as connection status, supporting role, and topological importance that might serve as reference for the integrated transportation planning of vital regions and cities.
integrated transportation; transportation planning; complex network; basic framework; stereoscopic transportation
U113
A
10.19961/j.cnki.1672-4747.2021.06.012
1672-4747(2021)04-0098-08
2021-06-11
2021-07-09
2021-07-12
2021-06-11~06-12; 06-27~06-28; 07-08~07-09
国家自然科学基金项目(71173177)
张勤宇(1997—),男,湖北宜昌人,博士研究生,研究方向为复杂网络与交通网络,E-mail:zqy715@my.swjtu.edu.cn
帅斌(1967—),男,四川乐山人,教授,研究方向为交通运输政策与宏观决策,E-mail:shuaibin@swjtu.edu.cn
张勤宇,帅斌,吕敏. 基于复杂网络的国家综合立体交通网主骨架分析[J]. 交通运输工程与信息学报,2021, 19(4): 98-105.
ZHANG Qin-yu, SHUAI Bin, LV Min. Analysis of the Basic Framework of the National Integrated Stereoscopic Transportation Network Based on Complex Network Theory[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 98-105.
(责任编辑:李愈)

