考虑排放约束的电动汽车混行交通路网均衡模型

李 浩，陈 浩，陆 续，涂辉招

考虑排放约束的电动汽车混行交通路网均衡模型

李 浩，陈 浩，陆 续，涂辉招

(同济大学，交通运输工程学院；道路与交通工程教育部重点实验室，上海 201804)

随着电动汽车的推广和使用，电动汽车与燃油汽车在路网中交互运行，形成了混行交通环境。本文构建考虑排放约束和途中充电的电动汽车混行交通路网均衡模型。首先，分别定义了电动汽车用户与燃油汽车用户的出行成本函数，其中电动汽车用户出行成本包含行驶时间、充电排队时间及充电时长。其次，构建了考虑排放约束的混行交通路网均衡模型，证明了解的唯一性，推导了模型对应的KKT条件，且与Wardrop第一原理等价。然后，将均衡模型表述为包括用户均衡条件、排放约束、守恒约束的互补性条件形式，通过引入间隙函数，进一步将其转化为等价的无约束最优化问题，并利用基于梯度的算法进行求解。最后，通过算例验证了均衡模型及算法的有效性，结果表明：(1)考虑路网排放约束将影响混行交通量和充电站充电流量空间分布；(2)总需求和电动汽车渗透率不变的条件下，提高减排力度会导致路网总行程时间的增加；(3)给定减排力度时，可以确定路网总行程时间最小时对应的电动汽车最优渗透率。

混行交通路网模型；间隙函数；电动汽车；排放约束；减排力度；最优渗透率

0 引 言

随着传统燃油汽车保有量的不断增加，其尾气排放所引起的交通环境污染问题日益突出，能源供需矛盾也日益凸显[1]。在城市交通管理中，决策者不仅要考虑路网运行效率，也要控制尾气排放造成的环境污染。因此，将排放约束考虑到交通路网模型中也逐渐成为国内外交通领域研究的热点，考虑的方法包括定义广义费用函数[2-3]、设置路段排放约束[4]、路网排放约束与路段排放约束的结合[5]等多个方面。

相较于传统燃油汽车，电动汽车具有节能环保的优势，被认为是实现节能减排的重要途径之一，拥有十分广阔的市场前景[6]。由于电池技术导致的续航里程有限[7]和充电基础服务设施不完善，电动汽车用户普遍存在里程焦虑心理，其出行行为与燃油汽车用户存在较大差异。关于电动汽车的路网均衡问题，也受到学者们的广泛关注。Jiang等[8]最早提出了考虑电动汽车的路网模型，在模型中加入了电动汽车续航里程的约束。He等[9]研究了里程焦虑心理以及充电行为对路网均衡的影响。此外，他考虑了路段电量消耗与路段流量的关系，提出了动态电量消耗下的UE条件与数学模型。部分学者[10-11]认为里程焦虑对出行行为的作用更可能发生在出行链层面(Trip- Chain Level)而不是出行层面(Trip Level)上，并将出行链作为用户出行决策的基本单元，研究了链式出行行为以及续航里程限制对交通网络流量分布的影响。Xie等[12]对里程约束的研究更加深入，他进一步考虑了随机里程约束分别服从离散型和连续型分布的情况，构建了凸优化模型和变分不等式模型，并采用梯度投影法进行求解。

但上述研究只考虑了电动汽车，没有考虑燃油汽车与电动汽车混行的交互影响。Jiang等[13-14]首次构建了燃油汽车和电动汽车同时存在的路网模型，并提出了线性逼近算法和二次逼近算法两种算法。杨扬等[15]和叶露等[16]提出了随机性用户均衡下的混合交通路网模型。Cen等[17]和Huang等[18]分别研究了即时充电需求(Immediate Charging Need)和随机充电需求对路径选择策略以及路网流量分布的影响。Zhang等[19]和Ferro等[20]则对多模式充电(Multi-Modal Recharge)进行了讨论。Xu等[21]指出He等[9]提出的动态电量消耗下的UE均衡条件忽略了某些特殊场景，并给出了完整的UE条件。Liu等[22]进一步针对Xu等[21]提出的UE条件构建了等价的非线性互补模型，并提出了相应的迭代算法。环境污染排放问题并未在上述研究中体现，在笔者的了解范围内，仅有徐若辰等[23]在混合交通路网模型中考虑了路段排放约束，并提出了一种基于动态投影系统的算法求解带非线性边界约束的路网均衡问题，但未考虑电动汽车途中充电的情况。

综上所述，考虑电动汽车与燃油汽车混行的路网模型研究很少关注环境污染问题，少量的考虑排放污染的混合路网模型研究缺少对电动汽车用户途中充电行为的模拟，难以刻画由于需要途中充电引起的路径选择变化及其对充电需求、路径流量空间分布的影响。因此，本文构建考虑环境污染排放约束的燃油汽车与电动汽车共 存的混行路网模型，主要包含：(1)考虑路网排 放约束；(2)考虑电动汽车用户的途中充电行为；(3)考虑用户里程焦虑、途中充电次数约束，以及非满电状态的任意初始荷电状态(State of Charge, SOC)条件下的路径规划；(4)考虑途中充电排队时间和充电时长对电动汽车用户充电路径选择行为的影响；(5)分析路网排放约束以及减排力度对交通量空间分布的影响，并对电动汽车最优渗透率进行研究。

1 符号定义

路段行驶时间使用BPR函数，如下式所示：

2 用户出行成本

在构建路网模型之前，首先定义电动汽车用户和燃油汽车用户的出行成本。

2.1 电动汽车用户出行成本

通常研究假设电动汽车出发前为满电状态[8, 13]，Wang等[10]和Xie等[12]考虑了初始电量为固定值、离散型分布、连续型分布的情形，但没有考虑途中充电。本文与He等[9]相同，初始电量可以取任意小于电动汽车电池容量的值。在初始电量满足出行要求时，不需要途中充电。在初始电量不足以完成整个出行时，会考虑在公共充电站进行途中充电。途中充电涉及充电站选择以及路径选择，本文定义考虑途中充电的电动汽车用户出行成本包含路径行驶时间、充电排队时间和充电时长。

(1)路径行驶时间

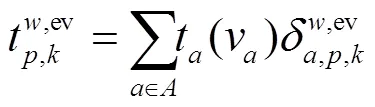
(2)充电排队时间

在电动汽车路网模型的文献研究中，大多数研究假设充电排队时间为一固定值[9,15]。近年来，Xu等[21]和Liu等[22]考虑了充电排队时间与车流量的关系，但主要针对换电站(Battery Swapping Station)进行。张维戈等[24]通过对电动出租车实际运营数据的分析，发现充电排队系统类属M/G/k排队模型，并给出了平均等待时间的近似公式，能更加真实地反映实际充电排队时间。本文选用M/M/S排队模型计算平均排队时间，如下式所示：

(3)充电时长

本文与Zhang等[25]和李浩[26]相同，假设电动汽车用户在充电时最多选择充至80%，充电函数满足线性函数这一假设，且实际充电电量并非要达到满电状态。

当初始电量足够支撑完成整个行程，且满足舒适里程时，充电电量为0。

当初始电量不能满足保证舒适里程的出行时，如果不选择最优充电策略，则在充电站的充电量可以是很多值，到达终点的剩余电量也可以是大于等于舒适里程的很多值，路网模型的解不唯一。因此，在假设途中充电时选择最优充电策略，保证解的唯一性。

(4)出行成本

2.2 燃油汽车用户出行成本

3 考虑排放约束的路网模型及算法

本文构建了考虑排放约束的双层规划模型，上层模型为基于Warodrop用户均衡原理的路网均衡模型，下层是最短路径规划模型。在求解过程中，首先初始化流量，使用路径规划模型求解最短路径，然后进行流量分配，根据配流结果更新路段和路径出行成本，再进行最短路径求解，进行新的流量分配，重复以上步骤直至均衡。路网分配与最短路径生成交互影响，最终所有使用的路径组成路径集。

3.1 上层模型—— 路网均衡模型构建

基于Beckmann提出的针对Wardrop用户均衡原理构建的模型，本文提出的混行路网均衡模型可以描述成如下非线性规划问题，其目标函数如式(10)所示，包含路段行驶时间函数对路段流量的积分求和、充电排队时间函数对充电流量的积分求和以及总充电时长：

约束条件为：

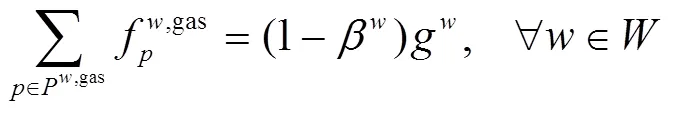
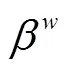
3.2 下层模型—— 路径规划模型

3.3 模型性质

3.3.1 上层模型性质

路网均衡模型目标函数(10)的Hessian矩阵如下式：

式中，目标函数关于路段流量与充电站充电流量的二阶偏导分别为下两式所示(同李浩等[26])：

由式(32)和(33)可得目标函数的Hessian矩阵正定，因此目标函数为严格凸函数。同时约束条件(11)～(17)均为线性约束。因此，该问题可以看成一个目标函数为严格凸函数、约束条件为线性的凸优化问题，该问题的路段流量、充电站充电流量有唯一最优解。通过引入拉格朗日乘子，得到拉格朗日函数如下：

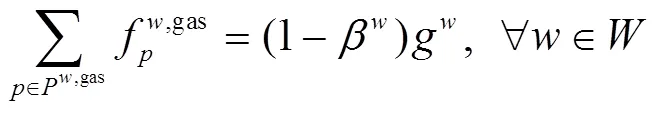
3.3.2 下层模型性质

下层路径规划模型是典型的0-1整数规划问题，对于电动汽车用户是在传统的最短路径问题上增加了充电电量、剩余电量和途中充电次数的约束，路径模型中边的权值是行驶时间，在节点中加入了充电排队时间、充电时长两个参数，求解目标是出行成本(见公式(8))最小的路径。本文用专业软件Gurobi进行了求解。

3.4 双层规划模型算法

3.4.1 原问题转化

因为包含约束条件(17)，3.1中的路网均衡模型无法直接使用Frank-Wolfe算法、MSA(Method of Successive Average)算法、GP(Gradient Projection) 算法等进行求解。针对带不等式约束下的最优化问题，Xu等[4]将模型转化为了非线性互补问题(Nonlinear Complementarity Problem，NCP)，将其表达为三个互补性条件，并引入了Lo和Chen[27]提出的间隙函数(Gap Function)，采用基于梯度的算法进行求解，这也为本文的求解算法提供了借鉴。

当模型有解时，3.1中的模型可以转化为式(35)～(37)、式(38)～(40)、式(41)～(43)、式(46)～(48)、式(49)～(51)五个互补性条件。其中，前两个为用户均衡条件，第三个为路网排放约束，最后两个为守恒约束：

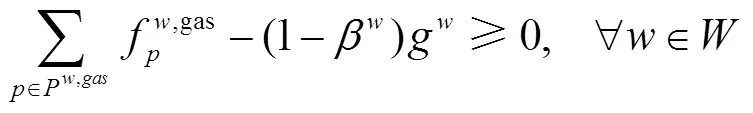
本文使用Lo和Chen提出的间隙函数，如下式所示：

并构造相应的函数，如下式所示：

3.4.2 双层规划问题求解算法

模型的求解算法具体步骤如下：

Step0 初始化。

4 数值分析

4.1 算例路网介绍

图1 算例路网

4.2 考虑路网排放对交通量空间分布的影响分析

图2给出了收敛指标与迭代次数的关系，可以看出路网均衡求解算法是收敛的。如果将收敛指标阈值设为0.001，迭代34次后模型收敛到均衡解。

迭代次数

分别对不考虑和考虑路网排放约束的路网模型进行求解，并对模型最优解对应的路段流量分布(见图3)、充电站充电流量分布(见图4)，以及燃油汽车用户路径出行成本(见表1)进行对比分析。由于本文取二氧化碳排放因子为固定值，单个燃油汽车用户在路径上产生的二氧化碳排放量仅与路径长度有关，如公式(18)所示。

图3 是否考虑路网排放约束的路段流量分布对比

图4 是否考虑路网排放约束的充电站充电流量分布对比

当考虑路网排放约束时，长度更长的路径单位流量的环境外部性成本更大，需要收取的外部性成本对应的费用更高。从表1可以看出，考虑排放约束的路网均衡下，同一OD对所使用的路径一般化出行成本相等。考虑排放约束后，OD对1—3间路径长度更长的路径1—6—13—19上的部分流量分配到了长度更短的路径1—5— 7—10—16。OD对4—2间，路径长度更长的路径4—12—14—15上的部分流量分配到了长度更短的路径3—5—7—9—11。

表1 考虑和不考虑路网排放约束的燃油汽车用户路径流量和成本

图3路段流量分布对比可以看出，当考虑路网排放约束时，更短路径上的路段5、7、9等的流量明显增加，更长路径上的路段12、14、15等的流量明显减少。从图4充电站流量对比中可以看出，燃油汽车用户流量分布对电动汽车用户的充电行为产生了影响。考虑环境排放约束，充电站5、7、11的充电流量降低，充电站8、9、10的充电流量增加。考虑路网排放约束和环境外部性成本，对混合交通路网均衡、交通量和充电流量的空间分布有显著影响。

4.3 减排力度的影响分析

图5 路段流量随减排力度变化的曲线

图6 电站充电流量随减排力度变化的曲线

图7展示了总行驶时间、总充电排队时间、总充电时长和总路径出行时间(前三项之和)随减排力度变化的曲线。结合图5和图7可知，随着减排力度的增加，即通过燃油税等形式所施加的外部性成本逐渐增加，迫使越来越多的燃油汽车流量聚集到路段7、9、10上，导致总行驶时间、总出行时间不断上升。由于总充电时长(100至400 min左右)和总充电排队时间(100 min左右)与总出行时间相差较大，所以折线图7中总充电时长和总充电排队时间不明显。

图7 总行驶时间、总充电排队时间、总充电时间、总出行时间随减排力度变化的曲线

当减排力度为10%时，模型无解，说明现状路网无法实现10%的减排目标。

4.4 最优电动汽车渗透率

之前分析均是在特定的电动汽车渗透率下进行的。在保持总出行需求不变的前提下，可以通过提高电动汽车渗透率实现进一步的节能减排。但在不改善充电服务基础设施的前提下，一味地提高电动汽车渗透率，可能会造成严重的充电站充电排队现象，降低电动汽车用户的出行体验，同时导致总充电排队时间的增加。

本文定义路网总出行时间(总行驶时间、总充电排队时间、总充电时长之和)最小时对应的电动汽车渗透率为电动汽车最优渗透率。在总出行需求和路网基准总碳排放量不变时，不同减排力度将对应不同的电动汽车最优渗透率。

以减排力度8%为例，总行驶时间、总充电排队时间、总充电时长和总出行时间随电动汽车渗透率变化的曲线如图8所示。当电动汽车渗透率从20%逐渐上升到30%时，燃油汽车用户出行需求减少，因路网排放约束的外部性成本导致的燃油汽车流量分布过度集中的现象得到缓解，总行驶时间和总出行时间显著下降。当电动汽车渗透率从30%不断增加时，因为受到充电站容量配置的制约，充电需求不断增加所引起的充电排队段产生交通拥堵，总行驶时间也开始逐渐增加，使得总出行时间不断增加。因此可得，当减排力度为8%时，路网的电动汽车最优渗透率为30%。

图8 总行驶时间、总充电排队时间、总充电时长、总出行时间随电动汽车渗透率变化的曲线

对于交通管理者，提高电动汽车渗透率能够显著降低路网总碳排放量，有效实现节能减排的目标。但在提高电动汽车渗透率的同时，需要合理改善充电基础设施的容量配置，避免总充电排队时间的迅速增加。此外，合理改善充电站布局，可以缓解因充电需求增加产生的交通拥堵。

5 结 语

本文针对燃油汽车与电动汽车混行的交通环境，构建了考虑电动汽车用户里程焦虑、可途中充电和非满电初始电量的路径生成模型，建立了考虑环境污染排放约束的混行交通路网均衡双层规划模型，其中上层模型为路网均衡模型，下层模型为最短路径规划模型。通过研究双层模型的性质，引入间隙函数，将原有问题转化为等价的无约束最优化问题，并提出了基于梯度的求解算法。最后，通过算例验证了模型和算法的有效性。

研究表明：(1)考虑路网排放约束的路网模型，相当于考虑包含排放约束外部性的一般化成本的多用户均衡，排放约束对混行交通量和充电站充电流量的空间分布具有显著影响，可以通过对该外部性成本征收燃油税、排放收费等形式保证排放约束的实施；(2)提高减排力度会带来总行驶时间的增加；(3)当给定减排力度时，可以确定路网总出行时间最小时对应的电动汽车最优渗透率。随着减排力度的增加，电动汽车最优渗透率会逐渐提高。

后续研究可以针对电动汽车的最优渗透率，构建双层规划模型，将本文提出的混行路网模型作为下层模型，上层模型则以路网总出行时间最小为目标，求解最优渗透率。其次，可以拓展到更大规模的路网来验证模型和算法的有效性。对于文中的凸优化模型也可以继续探索其他高效的求解算法[29]。

[1] 马建, 刘晓东, 陈轶嵩, 等. 中国新能源汽车产业与技 术发展现状及对策[J]. 中国公路学报, 2018, 31(8): 1-19.

[2] 杨文国, 高自友. 考虑环境因素的广义用户平衡和广义系统最优配流模型[J]. 中国公路学报, 2003, 16(4): 73-77.

[3] 熊伟, 严新平. 基于路径的算法求解考虑排放的交通分配模型[J]. 交通运输工程学报, 2009, 9(3): 71-75, 97.

[4] XU X, CHEN A, CHENG L. Reformulating environmentally constrained traffic equilibrium via a smooth gap function[J]. International Journal of Sustainable Transportation, 2015, 9(6): 419-430.

[5] 张鑫, 王京梅, 吴珂琪, 等. 低碳排放约束下交通网络均衡分析研究[C]//中国智能交通协会第十三届中国智能交通年会大会论文集. 北京: 中国智能交通协会, 2018: 44-53.

[6] 《中国公路学报》编辑部. 中国汽车工程学术研究综述·2017[J]. 中国公路学报, 2017, 30(6): 1-197.

[7] 马建, 张大禹, 赵轩, 等. 基于随机加权自适应容积卡尔曼的电池SOC估计[J]. 中国公路学报, 2019, 32(11): 234-244.

[8] JIANG N, XIE C, WALLER T. Path-constrained traffic assignment: model and algorithm[J]. Transportation Research Record Journal of the Transportation Research Board, 2012, 2283: 25-33.

[9] HE F, YIN Y, LAWPHONGPANICH S. Network equilibrium models with battery electric vehicles[J]. Transportation Research Part B: Methodological, 2014, 67: 306-319.

[10] WANG T G, XIE C, XIE J, et al. Path-constrained traffic assignment: a trip chain analysis under range anxiety[J]. Transportation Research Part C: Emerging Technologies, 2016, 68: 447-461.

[11] 谢驰, 白婷, 王同根. 里程焦虑下的电动汽车交通网络均衡[J]. 中国科技论文, 2017, 12(19): 2161-2165, 2171.

[12] XIE C, WANG T G, PU X, et al. Path-constrained traffic assignment: modeling and computing network impacts of stochastic range anxiety[J]. Transportation Research, 2017, 103: 136-157.

[13] JIANG N, XIE C. Computing and analyzing mixed equilibrium network flows with gasoline and electric vehicles[J]. Computer Aided Civil & Infrastructure Engineering, 2014, 29(8): 626-641.

[14] JIANG N, XIE C, DUTHIE J C, et al. A Network equilibrium analysis on destination, route and parking choices with mixed gasoline and electric vehicular flows[J]. EURO Journal on Transportation and Logistics, 2014, 3(1): 55-92.

[15] 杨扬, 姚恩建, 王梅英, 等. 电动汽车混入条件下的随机用户均衡分配模型[J]. 中国公路学报, 2015, 28(9): 91-97.

[16] 叶露, 郭倩芸, 倪舒晨, 等. 混合交通网络充电站选址模型[J]. 交通运输工程与信息学报, 2019, 17(4): 97-104.

[17] CEN X, LO H K, LI L, et al. Modeling electric vehicles adoption for urban commute trips[J]. Transportation Research Part B: Methodological, 2018, 117: 431-454.

[18] HUANG Y, KOCKELMAN K. Electric vehicle charging station locations: elastic demand, station congestion, and network equilibrium[J]. Transportation Research Part D: Transport and Environment, 2020, 78: 1-16.

[19] ZHANG X, REY D, WALLER S T, et al. Range- constrained traffic assignment with multi-modal recharge for electric vehicles[J]. Networks and Spatial Economics, 2019, 19(2): 633-668.

[20] FERRO G, MINCIARDI R, ROBBA M. A user equilibrium model for electric vehicles: joint traffic and energy demand assignment[J]. Energy, 2020, 198: 1-10.

[21] XU M, MENG Q, LIU K. Network user equilibrium problems for the mixed battery electric vehicles and gasoline vehicles subject to battery swapping stations and road grade constraints[J]. Transportation Research Part B: Methodological, 2017, 99: 138-166.

[22] LIU Z, SONG Z. Network user equilibrium of battery electric vehicles considering flow-dependent electricity consumption[J]. Transportation Research Part C: Emerging Technologies, 2018, 95: 516-544.

[23] 徐若辰, 钟任新. 基于动态投影系统的带非线性边界约束混行路网均衡模型求解算法[J]. 科学技术与工程, 2019, 19(12): 325-332.

[24] 张维戈, 陈连福, 黄彧, 等. M/G/k排队模型在电动出租汽车充电站排队系统中的应用[J]. 电网技术, 2015, 39(3): 724-729.

[25] ZHANG Y, ALIYA B, ZHOU Y, et al. Shortest feasible paths with partial charging for battery-powered electric vehicles in smart cities[J]. Pervasive and Mobile Computing, 2018, 50: 82-93.

[26] 李浩, 陈浩. 考虑充电排队时间的电动汽车混合交通路网均衡[J/OL]. 吉林大学学报(工学版): 1-9[2020-12- 17]. https: //doi. org/10. 13229/j. cnki. jdxbgxb20200421.

[27] LO H K, CHEN A. Traffic equilibrium problem with route-specific costs: formulation and algorithms[J]. Transportation Research Part B: Methodological, 2000, 34(6): 493-513.

[28] 徐建闽. 我国低碳交通分析及推进措施[J]. 城市观察, 2010 (4): 13-20.

[29] NIE Y, ZHANG H M, LEE D H. Models and algorithms for the traffic assignment problem with link capacity constraints[J]. Transportation Research Part B: Methodological,2004, 38: 285-312.

Mixed Traffic Network Equilibrium with Battery Electric Vehicles Considering Emission Constraints

LI Hao, CHEN Hao, LU Xu, TU Hui-zhao

( College of Transportation Engineering; Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China)

With the promotion and use of electric vehicles, electric and fuel vehicles operate in a road network interactively, thus forming a mixed traffic environment. In this study, a mixed traffic network model that considers emission constraints is developed. First, the utility functions of users of battery electric and fuel vehicles are defined, with travel time, charging queuing time, and charging time taken as utility components for users of battery electric vehicles. A corresponding mixed traffic network equilibrium model is then established. We prove the uniqueness of the model solution and derive Karush-Kuhn-Tucker conditions corresponding to the mixed traffic network model, which is proven to be equivalent to Wardrop’s first principle. Third, the equilibrium model is transformed into complementary conditions that include user equilibrium conditions as well as emission and conservation constraints. A gap function is introduced and reformulated into an equivalent unconstrained optimization problem, which is then solved by a gradient- based algorithm. Finally, the effectiveness of both the model and algorithm are verified through an example network application. The results are as follows. ① Road network emission constraints influence the spatial distribution of mixed traffic flows and charging demands; ② An increase in emission reductions leads to an increase in total network travel time; ③ Given emission reductions, the optimal penetration rate of battery electric vehicles corresponding to the minimum total network travel time can be determined.

mixed traffic network modeling; gap function; battery electric vehicles; emissions constraints; emission reductions; optimal penetration rate

U491.2+62

A

10.19961/j.cnki.1672-4747.2021.03.022

1672-4747(2021)04-0024-13

2021-03-22

2021-07-19

2021-07-26

2021-03-22～04-01；06-07～06-15；07-17～07-19

国家自然科学基金项目(71971162)；上海市科委重点项目(19DZ1209402)

李浩(1982—)，女，教授，博士生导师，博士，研究方向为多模式交通出行行为与路网模型，E-mail：haolitj@tongji.edu.cn

涂辉招(1977—)，男，教授，博士生导师，博士，研究方向为交通风险管理与自动驾驶，E-mail：huizhaotu@tongji.edu.cn

李浩，陈浩，陆续，等. 考虑排放约束的电动汽车混行交通路网均衡模型[J]. 交通运输工程与信息学报，2021, 19(4): 24-35, 117.

LI Hao, CHEN Hao, LU Xu, et al. Mixed Traffic Network Equilibrium with Battery Electric Vehicles Considering Emission Constraints[J]. Journal of Transportation Engineering and Information, 2021, 19(4): 24-35, 117.

(责任编辑：刘娉婷)